
 ‘.$_COOKIE[’email’].’ Выход’ ); /*
‘.$_COOKIE[’email’].’ Выход’ ); /*
‘ ); if ( isset($g_sVIPto) ) echo( ‘Дата окончания VIP статуса: ‘.$g_sVIPto.’ ‘ ); else echo( ‘VIP статуса нет. Как получить ?’ ); echo( ‘
‘ ); > else < // Если юзер НЕавторизованный : $redirect_uri = rawurlencode( ‘//www.math-solution.ru/parts/login.php?backUrl=’.$_SERVER[‘REQUEST_URI’] ); //
Вход:
Построение графиков функций: калькулятор онлайн
С помощью нашей программы вы сможете онлайн построить графики функций.
Программа работает в вашем браузере, её не нужно устанавливать на компьютер.
Зачем нужно строить графики функций?
В каких случаях может пригодиться построение графиков функций?
Ниже приводятся некоторые примеры использования построения графиков функций при решении различных математических задач.
1. При решении уравнений

Линейная функция и ее график. 7 класс.
Если вам нужно решить уравнение, то вы можете построить график функции слева и справа от знака равенства и посмотреть на пересечение этих графиков.
Точки пересечения построенных графиков функций это и есть решения исходного уравнения.
Если графики не пересекаются, значит решений нет.
Например, нужно решить уравнение ( x^2-3x+1 = x-1 )
Строим графики таких функций:
( f(x) = x^2-3x+1 )
( g(x) = x-1 )
Видно, что у этих графиков две точки пересечения.
Координата ( x ) этих точек и есть решение исходного уравнения: ( x_1 = 0,6 ; x_2 = 3,4 )
2. При решении неравенств
Например, нужно решить неравенство ( x^2-3x+1 Вы вошли как
Выход Вход
Источник: www.math-solution.ru
Сайт калькулятор для построения графиков Линейной функции

Единственный в мире Музей Смайликов
Самая яркая достопримечательность Крыма

Скачать 25.34 Kb.
«Сайт калькулятор для построения графиков Линейной функции»
Выполнил: ученик 9 “Б” класса
информатики Казаченко А.В
С построением графиков линейной функции возникают проблемы у школьников 7-9 классов. Но это совсем не сложно. Поэтому я решил создать сайт с калькулятором, который будет строить график линейной функции, с пояснением. Этим сайтом могут пользоваться любые желающие, а также ученики школы.
Цель: Создание web-сайта в открытом доступе в интернете, чтобы другие люди могли строить графики линейных функции.
- Обобщить имеющиеся знания о линейной функции;
- Найти новую информацию о линейной функции;
- Узнать в каких областях знаний применяется линейная функция;
- Создать сайт с калькулятором линейной функции:
- а) Изучить основы языков html и css;
- б) Разработать концепцию и структуру сайта;
- в) Результат работы оформить в виде действующего сайта;
- г) Загрузка сайта в интернет, на выбранном хостинге;
Построить график ЛИНЕЙНОЙ функции и найти:
Функция – одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира. Путь к появлению понятия функции заложил в XVII веке французский философ и математик Рене Декарт (1596–1650). Он первый ввёл в математику понятие переменной величины.
Чтобы освободить алгебру от геометрического языка, Декарт ввёл фиксированный единичный отрезок и стал рассматривать отношение других отрезков к нему. Он установил соответствия между числами и отрезками на прямой и, таким образом, ввел алгебраический метод в геометрию.
Появилась возможность изображать зависимость величин графически на координатной плоскости, числа – отрезками. При записи зависимостей между величинами, он стал применять буквы: для переменных и неизвестных величин Декарт принял обозначения x, y, z, …, а для величин известных и постоянных – a, b, c и т.д. Как известно, эти обозначения применяются в математике до сегодняшнего дня. Отношения между известными и неизвестными величинами Декарт выражал в виде уравнений, в которых все величины заменил длинами отрезков.
В своей «Геометрии» в 1637 году Декарт дает понятие функции, как изменение ординаты точки в зависимости от изменения ее абсциссы.
ОПРЕДЕЛЕНИЕ ЛИНЕЙНОЙ ФУНКЦИИИ И ЕЕ СВОЙСТВА
- y – зависимая переменная (функция);
- x – независимая переменная (аргумент);
- k и b – некоторые числа (коэффициенты).
Свойства линейной функции:
При а > 0, функция возрастает (график идет сверху вниз);
Источник: topuch.com
Как построить график функции в Excel
Чтобы правильно построить линейный график функций в Excel необходимо выбрать точечную диаграмму с прямыми отрезками и маркерами. Естественно это не единственный, но весьма быстрый и удобный способ.
Для разного рода данных нужно использовать разные типы графиков. Убедимся в этом, разобрав практический пример с построением математического графика функций в Excel.
Построение графиков функций в Excel
Начнем из анализа и создания графика функций в Excel. Мы убедимся в том, что линейный график в Excel существенно отличается от графика линейной функции, который преподают в школе.
Линейная функция x=y имеет следующие значения: x1=0, x2=1, x3=7. Заполните таблицу этими значениями как показано на рисунке:
Выделите диапазон A1:B4 и выберите инструмент: «Вставка»-«Диаграммы»-«График»-«График с маркерами».
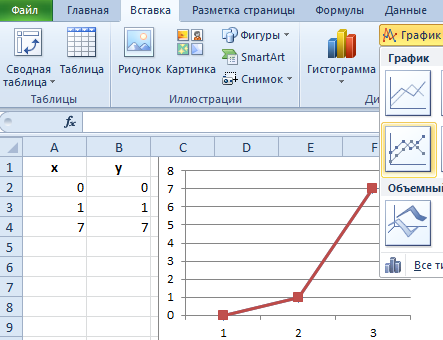
В результате у нас созданы 2 линии на графике, которые наложены одна сверх другой. Так же мы видим, что линии сломаны, а значит, они не соответствуют презентации школьному графику линейной функции. Излом линий, получается, по причине того, что на оси X у нас после значений: 0, 1 сразу идет значение 7 (упущены 2,3,4,5,6).
Вывод один: данный способ графического построения данных нам не подходит. А значит щелкните по нему левой кнопкой мышки (чтобы сделать его активным) и нажмите клавишу DELETE на клавиатуре, чтобы удалить его.
Как построить график линейной функции в Excel
Чтобы создать правильный график функций в Excel выберите подходящий график.
Выделите диапазон A1:B4 и выберите инструмент: «Вставка»-«Диаграммы»-«Точечная»-«Точечная с прямыми отрезками и маркерами».
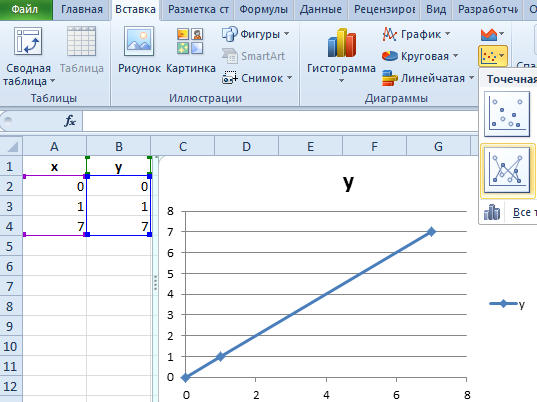
Как видно на рисунке данный график содержит одинаковое количество значений на осях X и Y. По умолчанию в шаблоне данного графика цена делений оси X равна 2. При необходимости ее можно изменить. Для этого:
- наведите курсор мышки на любое значение оси X чтобы появилась всплывающая подсказка «Горизонтальная ось (значений)» и сделайте двойной щёлочек левой кнопкой мышки;
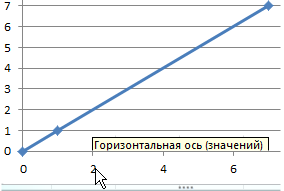
- в появившемся окне «Формат оси» выберите пункт опции: «Параметры оси»-«цена основных делений»-«фиксированное» и установите значение 1 вместо 2.
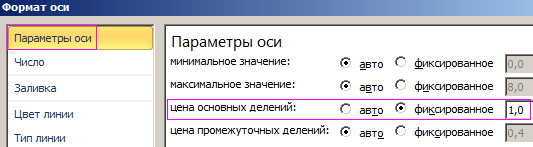
- нажмите на кнопку «Закрыть».
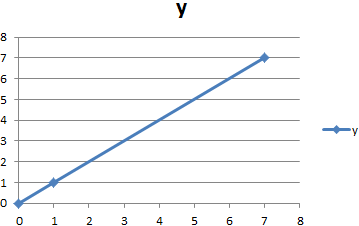
Теперь у нас отображается одинаковое количество значений по всем осям.
Очень важно понимать разницу в предназначениях графиков Excel. В данном примере мы видим, что далеко не все графики подходят для презентации математических функций.
Примечание. В принципе первый способ можно было-бы оптимизировать под отображение линейной функции, если таблицу заполнить всеми значениями 0-7. Но это не всегда работающее решение, особенно в том случае если вместо значений будут формулы изменяющие данные. Одним словом если нужно забить гвоздь лучше взять молоток, чем микроскоп. Несмотря на то, что теоретически гвозди можно забивать и микроскопом.
Не существует универсальных графиков и диаграмм, которыми можно отобразить любой отчет. Для каждого типа отчета наиболее подходящее то или иное графическое представление данных. Выбор зависит от того что и как мы хотим презентовать. На следующих примерах вы убедитесь, что выбор имеет большое значение. Существует даже целая наука «Инфографика», которая учит лаконично презентовать информацию с максимальным использованием графики вместо текста, насколько это только возможно.
- Создать таблицу
- Форматирование
- Функции Excel
- Формулы и диапазоны
- Фильтр и сортировка
- Диаграммы и графики
- Сводные таблицы
- Печать документов
- Базы данных и XML
- Возможности Excel
- Настройки параметры
- Уроки Excel
- Карта сайта
- Скачать примеры
Источник: exceltable.com