Программа для настройки пид

Цифровой регулятор — это программа, которая управляет некоторым процессом (регулирует). Получая входные данные с датчиков, она рассчитывает управляющее воздействие, обычно это некоторое число, которое в итоге с помощью электронной схемы преобразуется в реальное физическое воздействие. Задача регулятора — выйти на заданные показатели датчиков.

Допустим некий прибор на основе микроконтроллера должен регулировать температуру жала паяльника. К прибору подключён датчик температуры жала, который точно показывает текущую температуру жала — Tтек. Ну а пользователь прибора задаёт нужную температуру жала Тзад , которую прибор и должен поддерживать. Вот типичная задача регулирования. Попробуем самостоятельно придумать программу регулятор температуры жала для этого прибора.

Самое простое, что приходит в голову каждому, это включать паяльник когда заданная температура больше текущей и выключать когда меньше. Данный регулятор очень простой, он получает на входе текущую температуру паяльника, заданную температуру и возвращает число 1 (включить) или 0 (выключить паяльник). Далее микроконтроллер преобразует это число в высокий или низкий уровень напряжения на выводе и управляет паяльником. Это и есть программа регулятор — вполне рабочий вариант. Посмотрим какие у него есть минусы.

Настройка ПИД регулятора на практике

Так как прибор цифровой, то все в нем работает по «часам». Датчик температуры выдаёт данные только через какой-то интервал времени. Пусть это будет один раз в секунду. Теперь опишем свойства самого паяльника. При включении паяльника на полную мощность он нагревается за одну секунду на 20 градусов, а остывает за 1 сек на 5 градусов.

В таком случае, температура паяльника будет колебаться около заданной +/- 20 градусов.

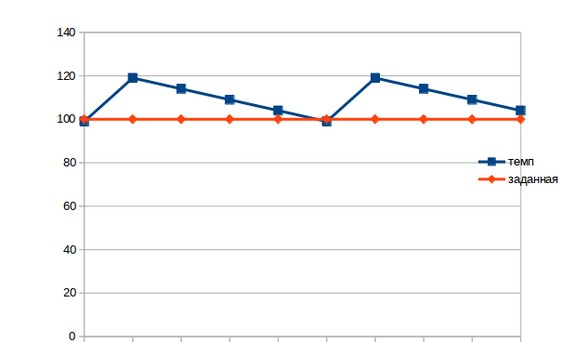
Почему так происходит? Как только мы включим паяльник, через одну секунду он добавит 20 градусов к своей температуре, ещё до того как мы узнаем, что эта самая температура превысила заданную. А потом будет долго остывать. Чтобы сделать реакцию паяльника более плавной, нужно управлять не просто включением его на полную мощность, а иметь возможно регулировать эту мощность. И вот тут как раз и нужен будет ПИД регулятор.

ПИД регулятор

Пусть наш прибор может регулировать мощность паяльника (например с помощью ШИМ модуляции) дискретно (с шагом в 1) в диапазоне от 0 до 10 единиц. 0 — выключен, 10 включён на полную мощность. Теперь, вместо обычного включения паяльника мы можем включить его с некоторой мощностью. Вопрос какая мощность нужна? ПИД регулятор как раз и служит для того, чтобы ответить на этот вопрос.

Эта программа автоматически рассчитает нужную мощность в каждый момент времени. Как расшифровывается аббревиатура ПИД:

Мощность которую нужно приложить к паяльнику в текущий момент времени складывается из трёх вышеперечисленных компонент. ПИД регулятор находит её автоматически. Разберём что это за компоненты, и как работает алгоритм.

Настройка ПИД регулятора балансирующего робота

Напомним, что в цифровой электронике нет непрерывных процессов, любая программа выполняется не мгновенно, а за какое-то количество тактов. Датчики выдают данные тоже с некоторой периодичностью. И ПИД регулятор тоже будет работать дискретно. Будем считать (и это очень важно), что программа регулятор вызывается строго через одинаковые промежутки времени (например, каждые 300мс) и вычисляет нужное управляющее воздействие.

Из чего состоит ПИД регулятор

Первый, он же самый простой и понятный компонент — это «П». Он так и называется «пропорциональный». Как он работает?

Пусть у нас есть Tтек и Тзад. Теперь вычтем одно из другого, получим ошибку E. Задача ПИД регулятора привести эту ошибку к 0. На выходе вычислений как раз и получается нужная мощность с которой должен работать паяльник. Итак, если у нас только один компонент, то будет такая формула:

P — рассчитанная мощность, Kpgain * Е — пропорциональный компонент, Kpgain — пропорциональный коэффициент, а Kpdiv — коэффициент делитель. В целочисленной арифметике, удобной для микроконтроллеров, лучше использовать два коэффициента, которые оба целочисленные.

Из этой формулы следует, что чем большую ошибку видит регулятор, тем большую мощность он подаёт на паяльник, чтобы быстрее уменьшить ошибку. Таким образом, если паяльник заметно остыл, то он будет включён на полную мощность, а по мере приближения к заданной температуре, регулятор будет подавать все меньшую мощность. Если производить измерения очень быстро и регулировать мощность тоже очень быстро, например 1000 раз в секунду или 10 000, то остальные коэффициенты будут не нужны и будет достаточно одной П компоненты. В таком диапазоне времени все нелинейные процессы становятся линейными. А вот если как у нас — раз в секунду, то они понадобятся.

Следующий компонент — И — интегральный. Он вычисляется чуть сложнее:

«И» компонент потому и называется интегральный, что по сути он накапливает, интегрирует, ошибку. Как мы предположили ранее, регулятор вызывается строго через равные промежутки времени dt. Поэтому, можно сказать, что Kigain содержит делитель . То есть получается, что «И» компонент отражает скорость изменения ошибки. Если процессы у нас линейные (как в нашем паяльнике) и заданная температура постоянна, то «И» в долгосрочной перспективе отражает ту мощность, при которой скорость нагрева паяльника равна скорости его остывания (что нам и нужно). «П» компонент долгосрочно будет стремиться к нулю, а в краткосрочной перспективе, будет учитывать мгновенные изменения во внешней среде. Например, если мы начали паять, паяльник стал остывать быстрее. «П» компонент отреагирует сразу.

Но у нас есть ещё третий компонент «Д». Он является производной скорости изменения ошибки, то есть отражается ускорение нагрева паяльника. Конечно, у паяльника оно равно 0, и этот компонент здесь не имеет смысла (но в других системах он очень важен, например в квадрокоптере), но все равно рассмотрим как он вычисляется. Пусть Ei-1 — ошибка посчитанная на предыдущем шаге, а Еi — текущая ошибка. Тогда «Д» будет вычисляться так:

«Д» является как бы тормозом, когда мы «перелетели» через заданную температуру. Когда ещё скорость изменения ошибки положительная, «Д» уже станет отрицательным и быстрее вернёт паяльник к заданной температуре, дополнительно уменьшая рабочую мощность.

Как рассчитать коэффициенты ПИД регулятора

Коэффициенты Kpgain, Kigain Kdgain (параметры ПИД регулятора) находятся опытным путём в процессе настройки регулятора и не меняются в процессе дальнейшей работы регулятора. ПИД регулятор отлично выполняет свою работу, однако, только тогда, когда регулируемая система не меняется. Например, в случае с паяльником, если мы дополнительно начнём охлаждать жало, то настроенный ПИД регулятор перестанет работать, так как дополнительное охлаждение потребует изменения коэффициентов настройки регулятора. Это нужно запомнить. В случае изменения динамической модели управляемой системы, требуется перенастроить параметры ПИД регулятора.

Как же можно подобрать коэффициенты опытным путём? Начнём с коэффициента Kpgain. Его подобрать проще всего. Будем постепенно увеличивать его пока система не начнёт колебаться около заданной температуры. Далее будем уменьшать Kpgain значение пока колебания не уменьшаться.

Вот это значение и будет самым оптимальным.

Чтобы подобрать Kigain нужно чуть уменьшить подобранный ранее коэффициент Kpgain . При этом ошибка станет положительной, мы будем не догонять заданную температуру. Вот в это время и начинаем увеличивать Kigain . «И» начнет интегрировать ошибку повышая мощность, пока опять не начнутся колебания. Они уже будут значительно меньше, чем в случае с одним коэффициентом.

«Д» подобрать сложнее. Нужно резко (импульсно) менять заданную температуру и смотреть, чтобы температура паяльник не «перелетала» заданную. Увеличивая Kdgain мы исключим «перелёты».

Как запрограммировать ПИД регулятор

Программируется ПИД регулятор на удивление просто.

Любой регулятор на языке программирования это функция, которая получает в качестве параметров данные датчиков и возвращает вычисленное значение управляющего воздействия. Сразу приведём пример типичной функции ПИД регулятора, а потом разберём как она работает и посмотрим как её использовать в реальном приборе на базе микроконтроллера.

Кажется сложным. Но на самом деле это не так. Начнём с определения функции. Функция принимает три параметра. hReference — заданное значение, hPresentFeedback — текущее значение с датчика и третий параметр структура с настройками конкретного объекта ПИД регулятора. Таким образом, функция может обслуживать сразу несколько ПИД регуляторов.

Вычисляем ошибку wError, и сразу считаем пропорциональную составляющую wProportional_Term. Все нужные коэффициенты находятся в структуре. Все вычисления производим в целочисленной системе, умножения в начале, а все деления в конце кода (для этого повышаем разрядность вычислений до 32 бит).

Далее считаем интегральный компонент. Если интегральный коэффициент равен нулю, то и вычислять нечего — интегральный компонент равен нулю. Накопленное значение интегральной компоненты храним в структуре «PID_Struct→pPID_Var→wIntegral». И добавляем туда опять же целую часть коэффициента умноженного на ошибку.

Теперь нужно разобраться с переполнением этого компонента. Заметим сразу, что типы здесь все знаковые — ошибка может быть как положительной, так и отрицательной. Очень важно корректно все сделать с точки зрения целочисленной математики ограниченных типов.

В этой части кода обрабатывается ситуация, когда к максимальному положительному числу для выбранной разрядности прибавили положительное число, то результат станет отрицательным! Это надо отследить и ограничить результат максимальным положительным числом. То же самое для отрицательной части.

Иногда бывает полезно сразу ограничить интегральную составляющую некими заранее известными лимитами. Например, у нас итоговая мощность лежит в интервале от 0 до 10. То и интегральный компонент не должен выходить за эти приделы (естественно после деления). Ну и в итоге нужно результат положить в структуру в интегральный компонент, его надо запомнить на следующий раз.

Теперь считаем дифференциальный компонент. Коэффициент умножаем на разницу текущей ошибки и предыдущей. После этого предыдущую ошибку заменяем на текущую.

И финальный подсчёт с учётом делителей всех трёх компонент. Возвращаем полученное значение мощности.

Пользоваться такой процедурой очень легко. Вызывать её нужно строго с одинаковой периодичностью, лучше с помощью прерываний по таймеру. А далее уже можно делать какие-либо управляющие действия.

Лучше сразу все коэффициенты (кроме делителей) делать в виде переменных, чтобы можно было быстро и легко настроить регулятор в процессе отладки. Коэффициенты можно менять либо через UART, либо с помощью ADC и переменного резистора или пошагово с помощью кнопок. А ещё это удобно делать сразу через программатор в режиме отладки кода. Напрямую с компьютера.

Тема ПИД регулятора очень объёмная, в интернет можно найти очень много статей посвящённых этому виду регулятора. На этом мы закончим знакомство с ним и перейдём к реальным приборам — паяльная станция. В этом приборе его и задействуем.

Источник: myowndevice.ru

Библиотека PID регулятора для Arduino v3.3

ПИД регулятор – мощный инструмент, позволяющий удерживать заданную величину (температура, скорость вала, положение) при помощи управляющего устройства (обогреватель, контроллер мотора, линейный привод). Вот отличная статья по теории, что такое ПИД регулятор, как он работает и как его настроить. А я предлагаю свою библиотеку для работы с PID на Arduino. ПИД регулятор выдаёт на выходе сигнал для плавного управления управляющим устройством (диммер, транзистор), если вам нужно реле – используйте библиотеку GyverRelay. Алгоритм ПИД регулятора выглядит так, можете использовать его напрямую в скетче:

void setup() < >void loop() < // (вход, установка, п, и, д, период в секундах, мин.выход, макс. выход) //analogWrite(pin, computePID(sensorRead, 30, 1.0, 2.0, 3.0, 0.02, 0, 255)); //delay(20); >// функция пид int computePID(float input, float setpoint, float kp, float ki, float kd, float dt, int minOut, int maxOut) < float err = setpoint — input; static float integral = 0, prevErr = 0; integral = constrain(integral + (float)err * dt * ki, minOut, maxOut); float D = (err — prevErr) / dt; prevErr = err; return constrain(err * kp + integral + D * kd, minOut, maxOut); >

БИБЛИОТЕКА

GyverPID v3.3

Библиотека классического PID регулятора для Arduino

• Быстрая и лёгкая библиотека
• Время одного расчёта около 70 мкс
• Режим работы по величине или по её изменению (для интегрирующих процессов)
• На выбор целочисленная или float модель вычисления
• Возвращает результат по встроенному таймеру или в ручном режиме

Поддерживаемые платформы: все Arduino (используются стандартные Wiring-функции)

УСТАНОВКА

• Библиотеку можно найти и установить через менеджер библиотек по названию GyverPID в:

• Arduino IDE (Инструменты/Управлять библиотеками)
• Arduino IDE v2 (вкладка “Library Manager”)
• PlatformIO (PIO Home, вкладка “Libraries”)

ДОКУМЕНТАЦИЯ

Документация

Логика работы

• Входной сигнал input — сигнал с датчика: температура, скорость, положение, и т.д;
• Установку setpoint — величина, к которой регулятор будет стараться регулировать входной сигнал (температуру, скорость, положение. )

• Kp — пропорциональный коэффициент, выходная величина будет увеличиваться пропорционально разнице входного сигнала и установки.
• Ki — коэффициент интегрирующей составляющей, отвечает за накапливающуюся ошибку, позволяет сгладить пульсации и нивелировать маленькую ошибку.
• Kd — коэффициент дифференциальной составляющей, отвечает за скорость изменения величины, позволяет уменьшить раскачку системы.

Инициализация

• GyverPID regulator; // инициализировать без настроек (всё по нулям, dt 100 мс)
• GyverPID regulator(kp, ki, kd); // инициализировать с коэффициентами. dt будет стандартно 100 мс
• GyverPID regulator(kp, ki, kd, dt); // инициализировать с коэффициентами и dt (в миллисекундах)

Режимы и настройки

Направление регулирования: зависит от того, в какую сторону направляется управляемая величина input при увеличении управляющего сигнала output . Например: охлаждение или нагрев, разгон или торможение, и т.д. По умолчанию стоит NORMAL — регулятор считает, что увеличение управляющего сигнала output увеличит входной сигнал input . Устанавливается командой setDirection(dir); // dir — NORMAL или REVERSE Режим работы: режим регулирования по ошибке входного сигнала ON_ERROR или по изменению входного сигнала ON_RATE . По умолчанию стоит ON_ERROR , его рекомендуется использовать в большинстве случаев, потому что большинство процессов — самоустанавливающиеся (температура нагревателя сама установится в своём максимуме, скорость мотора — тоже).

Режим ON_RATE рекомендуется использовать в интегрирующих процессах, в которых выходная величина влияет на скорость изменения входной величины, например положение моторизированного слайдера, который не остановится при управляющем сигнале, отличном от нуля. Таким процессом будет проще управлять в режиме ON_RATE . Устанавливается командой setMode(mode); // mode — ON_ERROR или ON_RATE Подробнее про этот режим смотри в самом конце документации, в разделе оптимизации интегральной суммы.

Пределы выхода: ограничение значения выходного сигнала, по умолчанию: 0-255 (для 8 бит ШИМ). Может быть установлено 0-180 для угла сервопривода, и т.д. Устанавливается командой setLimits(min, max); // установить пределы Время итерации: время итерации можно изменить в процессе работы (не знаю, зачем, но возможность есть). Время устанавливается в миллисекундах и влияет на функцию getResultTimer() , которая с этим периодом делает новый расчёт управляющего сигнала. Также это время входит в расчёт управляющего сигнала (в И и Д составляющей). Устанавливается командой setDt(dt); // установка времени итерации в мс

Установка/чтение параметров

Основные величины регулятора можно менять в любом месте программы любым удобным способом (кнопки, энкодер, передача через UART/GSM/WiFi, как угодно). Коэффициенты регулятора Kp , Ki и Kd можно устанавливать и читать напрямую как члены класса, например

regulator.Kp = 1.5; // установить regulator.Ki += 0.7; // изменить lcd.print(regulator.Kd); // читать

Время итерации меняется при помощи метода setDt() (см. выше). Величины регулятора (вход, установка, выход) также являются членами класса и к ним можно обратиться напрямую для чтения и записи:

regulator.input = 10; // ВХОД регулятора, например текущая температура regulator.setpoint = 20; // УСТАНОВКА регулятора, например необходимая температура analogWrite(regulator.output); // ВЫХОД с регулятора можно подавать напрямую на ШИМ или серво

Тип вычислений

Библиотека имеет режим целочисленных вычислений. Скорость вычислений особо не меняется, но код занимает меньше места и всё-таки должен выполняться быстрее. По умолчанию стоит режим чисел с плавающей точкой, в заголовочном файле библиотеки смотрите ключевое слово datatype , datatype будет float или int в зависимости от настройки: это некоторые переменные и функции. Настройка осуществляется дефайном перед подключением библиотеки:

#define PID_INTEGER #include «GyverPID.h»

Как работать с библиотекой?

Нужно скормить регулятору текущее значение величины в input , нужное значение в setpoint , провести расчёт при помощи getResult() или getResultTimer() , и после этого выходную величину output подать на управляющее устройство.

Делать это нужно часто для быстрых процессов (стабилизация частоты оборотов шпинделя станка под нагрузкой: dt берём около 10-50 мс), и не очень часто для медленных процессов (удержание заданной температуры бойлера: dt можно взять пару секунд, процесс очень инерционный). Функция getResult() делает расчёт в каждый свой вызов и возвращает output , а getResultTimer() делает расчёт только при срабатывании встроенного таймера. То есть getResult() нужно вызывать по своему таймеру (для продвинутых пользователей), а getResultTimer() нужно вызывать как можно чаще, он посчитает только тогда, когда это будет нужно по своему таймеру. После расчёта можно подавать управляющий сигнал (выходную величину output ) на управляющее устройство. Смотрите пример!

Как настроить коэффициенты?

Подбор коэффициентов ПИД регулятора — индивидуальная задача, зависящая от конкретных условий и «железа». Можно почитать статьи на эту тему: например эту, вот эту попроще, и вот эту посложнее. Первым делом нужно установить dt — об этом я писал выше. Маленький dt для быстрых процессов и побольше для медленных (инертных).

Dt влияет на расчёты при неизменных коэффициентах, поэтому dt лучше не менять во время настройки, чтобы не пришлось пересчитывать все остальные коэффициенты. Диапазон коэффициентов: 0.01 — 100, т.е. довольно широк и зависит напрямую от инертности системы и выбранного времени dt. Коэффициенты должны быть положительные, противоположное направление регулирования задаётся в setDirection() . В версии 3.0 появился автоматический тюнер коэффициентов, читай ниже.

Оптимизация интегральной суммы (экспериментально)

В реальной системе интегральная сумма может перенасыщаться и стать причиной неадекватного поведения регулятора, «заклинивания» его в крайних положениях. Библиотека предлагает несколько автоматических способов оптимизации интегральной суммы, остальную теорию можно почитать здесь. С версии 3.1 в библиотеке работает автоматическое ограничение интегральной суммы по выходным лимитам регулятора.

Ручная оптимизация

В версии 2.1 интегральная сумма вынесена в публичный доступ как член класса, к ней можно обратиться как regulator.integral (где regulator — ваше имя объекта). Интегральная составляющая суммирует ошибку по времени, и при слишком сильном накоплении может приводить к перерегулированию (например для инерционных систем, таких как обогреватель). Для наблюдения за её состоянием можно прочитать integral , и при необходимости, например, ограничить её диапазон ( regulator.integral = constrain(regulator.integral, -500, 500); каждый раз после вызова getResult() ) или даже обнулить ( regulator.integral = 0; ) по условию.

Режим интегрального окна

В версии 2.3 появился режим интегрального окна, как один из вариантов оптимизации интегральной суммы, может быть полезен для некоторых систем. В этом режиме интегральная сумма складывается из последних N измерений, где N задаётся при помощи дефайна PID_INTEGRAL_WINDOW . Для использования этого режима нужно прописать в скетче дефайн с указанием размера окна до подключения библиотеки.

#define PID_INTEGRAL_WINDOW 50 #include «GyverPID.h» // .

Будьте внимательны, внутри библиотеки будет создан массив указанного размера и займёт память! Используйте только в том случае, если понимаете как это работает и для чего оно нужно, а также есть возможность наблюдать за графиком и делать выводы!

Режим оптимизации интегральной суммы

В версии 3.0 появился новый режим автоматической оптимизации интегральной суммы: она автоматически ограничивается так, чтобы выходной сигнал не превышал установленные в setLimits() пределы, то есть инт. сумма не будет бесконечно расти или уменьшаться. В то же время резкие скачки значения с датчика (вход регулятора) вблизи пределов могут приводить к обнулению интегральной суммы, поэтому входной сигнал рекомендуется фильтровать. Для активации режима оптимизации интегральной суммы нужно прописать в скетче дефайн #define PID_OPTIMIZED_I до подключения библиотеки.

Режим «пропорционально скорости»

Выше была описана смена режима работы при помощи setMode(mode); , в режиме ON_RATE регулятор лучше справляется с интегрирующими процессами (например позиция вала мотора), но иногда хорошо работает и с нагревателями, уменьшая переполнение интегральной суммы и перерегулирование в целом. В этом режиме коэффициенты ведут себя иначе и их оптимальные значения отличаются от обычного режима, логика ручной настройки также отличается: коэффициент Kp теперь работает только в паре с Ki и настраивать их нужно вместе, причём в некоторых процессах Kp не даёт никакого эффекта при нулевом Ki, либо работает неадекватно. Смотри пример simulation_linear, в котором симулируется идеальный интегрирующий процесс. Реализация режима взята отсюда, там же есть теоретическое обоснование.

Автоматический тюнер коэффициентов 1

Тюнер тип 1

Автоматический калибровщик коэффициентов ПИД регулятора, метод «реле» http://auto-controls.blogspot.com/2009/10/pid-controllers-auto-tuning-relay.html. Данный тюнер лучше настраивает коэффициенты для удержания величины и парирования внешних возмущений. Примечание: тюнер позволяет найти более-менее приемлемые коэффициенты, при которых система будет работать. Эти коэффициенты не являются идеальными и их всё равно придётся покрутить вручную. Примечание: тюнер выдаёт коэффициенты для ПИ и ПИД регулятора. ПИ регулятор подразумевает, что коэффициент Д будет равен 0.

Как это работает?

1. Тюнер подаёт управляющий сигнал и ждёт стабилизации значения с датчика
2. Тюнер изменяет сигнал на некоторую величину (ступеньку)
3. Ждёт заданное время, затем меняет сигнал на ту же ступеньку, но в другую сторону
4. Начинается раскачка системы: при прохождении значения с датчика через значение стабилизации сигнал снова переключается
5. Производится анализ периода раскачки и её амплитуды, на основании этих данных вычисляются рекомендуемые коэффициенты

Как пользоваться библиотекой?

1. Направление : — NORMAL : увеличение выходного сигнала увеличивает сигнал с датчика (например обогреватель, мотор) — REVERSE : увеличение выходного сигнала уменьшает сигнал с датчика (например холодильник, тормоз)
2. Cигнал : базовый сигнал на управляющее устройство. Система будет ждать стабилизации по величине этого сигнала, и от него будет откладываться ступенька
3. Ступенька : величина, на которую будет изменяться сигнал в обе стороны от базового
4. Период : период опроса в ожидании стабилизации
5. Точность стабилизации : скорость изменения значения с датчика, ниже которой система будет считаться стабильной
6. Продолж. импульса : время в миллисекундах на первую раскачку
7. Период итерации : dt системы в мс, желательно должно совпадать с периодом ПИД регулятора

// цикл tuner.setInput(значение с датчика); // передаём текущее значение с датчика. ЖЕЛАТЕЛЬНО ФИЛЬТРОВАННОЕ tuner.compute(); // тут производятся вычисления по своему таймеру // tuner.getOutput(); // тут можно забрать новый управляющий сигнал analogWrite(pin, tuner.getOutput()); // например для ШИМ

3. Отладка и получение значений 3.1 Во время работы тюнера можно вызвать tuner.getAccuracy() — чем ближе его значение к 100, тем стабильнее на данный момент качается система и тем вычисляемые коэффициенты будут более близки к идеальным 3.2 Для наблюдения за тюнером через Serial есть готовые методы: — tuner.debugText() выводит текстовые данные (смотри скриншот в папке docs библиотеки) — tuner.debugPlot() выводит данные для построения графика через плоттер Arduino IDE (смотри скриншот в папке docs библиотеки) 3.3 Чтобы получить коэффициенты внутри программы (без Serial) желательно задать условие if (tuner.getAccuracy() > 95) и при наступлении этого условия получить коэффициенты:

tuner.getPI_p() — p для ПИ регулятора tuner.getPI_i() — i для ПИ регулятора tuner.getPID_p() — p для ПИД регулятора tuner.getPID_i() — i для ПИД регулятора tuner.getPID_d() — d для ПИД регулятора

Смотрите примеры в examples/autotune

Автоматический тюнер коэффициентов 2

Тюнер тип 2

Автоматический калибровщик коэффициентов ПИД регулятора, метод Cohen-Coon https://pages.mtu.edu/~tbco/cm416/cctune.html. Данный тюнер лучше настраивает коэффициенты для переходного процесса, например разогрев с одной температуры до другой. Примечание: тюнер позволяет найти более-менее приемлемые коэффициенты, при которых система будет работать. Эти коэффициенты не являются идеальными и их всё равно придётся покрутить вручную. Примечание: тюнер выдаёт коэффициенты для ПИ и ПИД регулятора. ПИ регулятор подразумевает, что коэффициент Д будет равен 0.

Как это работает?

1. Тюнер подаёт стартовый управляющий сигнал и ждёт стабилизации значения с датчика
2. Тюнер запоминает минимальное значение и подаёт конечный сигнал, ждёт стабилизации
3. Тюнер запоминает максимальное значение, снова подаёт начальный сигнал и ждёт стабилизации
4. Тюнер снова подаёт конечный сигнал
5. Зная полное время процесса, тюнер измеряет сигнал в определённых точках и по специальным формулам считает коэффициенты

Как пользоваться библиотекой?

1. Направление : — NORMAL : увеличение выходного сигнала увеличивает сигнал с датчика (например обогреватель, мотор) — REVERSE : увеличение выходного сигнала уменьшает сигнал с датчика (например холодильник, тормоз)
2. Начальный сигнал : стартовый сигнал на управляющее устройство
3. Конечный сигнал : конечный сигнал на управляющее устройство
4. Период : период опроса в ожидании стабилизации
5. Точность стабилизации : скорость изменения значения с датчика, ниже которой система будет считаться стабильной
6. Период итерации : dt системы в мс, желательно должно совпадать с периодом ПИД регулятора

// цикл tuner.setInput(значение с датчика); // передаём текущее значение с датчика. ЖЕЛАТЕЛЬНО ФИЛЬТРОВАННОЕ tuner.compute(); // тут производятся вычисления по своему таймеру // tuner.getOutput(); // тут можно забрать новый управляющий сигнал analogWrite(pin, tuner.getOutput()); // например для ШИМ

3. Отладка и получение значений 3.1 Во время работы тюнера можно вызвать tuner.getState() — вернёт номер текущего этапа работы. На 7-ом этапе можно забирать коэффициенты 3.2 Для наблюдения за тюнером через Serial есть готовые методы: — tuner.debugText() выводит текстовые данные (смотри скриншот в папке docs библиотеки) — tuner.debugPlot() выводит данные для построения графика через плоттер Arduino IDE (смотри скриншот в папке docs библиотеки) 3.3 Чтобы получить коэффициенты внутри программы (без Serial) желательно задать условие if (tuner.getState() == 7) и при наступлении этого условия получить коэффициенты:

tuner.getPI_p() — p для ПИ регулятора tuner.getPI_i() — i для ПИ регулятора tuner.getPID_p() — p для ПИД регулятора tuner.getPID_i() — i для ПИД регулятора tuner.getPID_d() — d для ПИД регулятора

Смотрите примеры в examples/autotune2

Список функций и методов библиотеки из файла .h

// ==== datatype это float или int, в зависимости от выбранного (см. пример integer_calc) ==== GyverPID(); GyverPID(float new_kp, float new_ki, float new_kd, int16_t new_dt = 100); // kp, ki, kd, dt datatype setpoint = 0; // заданная величина, которую должен поддерживать регулятор datatype input = 0; // сигнал с датчика (например температура, которую мы регулируем) datatype output = 0; // выход с регулятора на управляющее устройство (например величина ШИМ или угол поворота серво) datatype getResult(); // возвращает новое значение при вызове (если используем свой таймер с периодом dt!) datatype getResultTimer(); // возвращает новое значение не ранее, чем через dt миллисекунд (встроенный таймер с периодом dt) void setDirection(boolean direction); // направление регулирования: NORMAL (0) или REVERSE (1) void setMode(boolean mode); // режим: работа по входной ошибке ON_ERROR (0) или по изменению ON_RATE (1) void setLimits(int min_output, int max_output); // лимит выходной величины (например для ШИМ ставим 0-255) void setDt(int16_t new_dt); // установка времени дискретизации (для getResultTimer) float Kp = 0.0; float Ki = 0.0; float Kd = 0.0;

Источник: alexgyver.ru

Настройка ПИД-регулятора. Метод Циглера-Никольса.

Продолжаем начатую тему, посвященную работе ПИД-регулятора, и сегодня речь пойдет непосредственно и исключительно о настройке ПИД-регулятора. Начнем, как полагается, с теоретических моментов, затем же плавно перейдем к практическому примеру на базе регулятора температуры на STM32, созданному нами в той, первой, статье.

Настройка ПИД-регулятора. Теория.

И, собственно, данная настройка заключается в том, чтобы вычислить или подобрать оптимальные значения коэффициентов:

• K_p — коэффициент усиления пропорциональной составляющей
• K_i — коэффициент усиления интегрирующей составляющей
• K_d — коэффициент усиления дифференцирующей составляющей

По большому счету, при использовании ПИД-регулятора необходимо построить модель всей системы в целом и математически вычислить необходимые значения коэффициентов. В таком случае значения можно рассчитать очень точно. Но на практике математический расчет коэффициентов — задача далеко не тривиальная и требует глубоких знаний теории автоматического управления, поэтому в большинстве случаев используются другие, упрощенные, методы настройки.

Существует целый ряд различных способов, которые определяют вполне конкретные шаги, которые необходимо предпринимать. Мы же разберем один из них, а именно — метод Циглера-Никольса, ввиду того, что он получил наибольшее распространение и популярность.

Метод Циглера-Никольса.

Заключается он в последовательном выполнении следующих операций:

1. Обнуляем все коэффициенты регулятора.
2. Задаем некоторое целевое значение регулируемого параметра (например, температуры).
3. Постепенно начинаем увеличивать пропорциональный коэффициент и следим за реакцией системы.
4. При определенном значении K_p возникнут незатухающие колебания регулируемой величины.
5. Фиксируем это значение, а также период колебаний системы.

На этом практическая часть метода заканчивается. Из полученных значений рассчитываем коэффициенты:

K_p = 0.6cdot K \ K_i = (2cdot K_p)medspace/medspace T \ K_d = (K_pcdot T)medspace/medspace 8

Здесь K – тот самый коэффициент пропорциональной составляющей, при котором возникли колебания, а T – период этих колебаний. Рассмотрим псевдо-пример для получения более полного представления о данном процессе. Пусть при K_p равном 10, возникают колебания следующего рода:

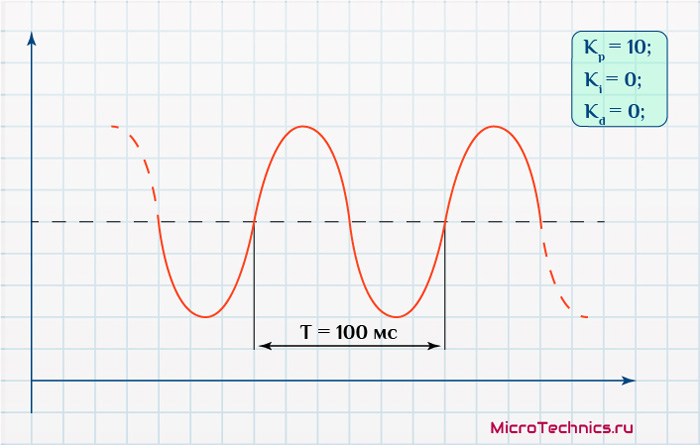
Период составляет 0.1 с. Производим расчеты по вполне конкретным формулам и получаем:

K_p = 0.6cdot 10 = 6 \ K_i = (2cdot 6)medspace/medspace 0.1 = 120 \ K_d = (6cdot 0.1)medspace/medspace 8 = 0.075

Все, на этом процедура окончена.

Метод довольно прост, но применить его можно далеко не всегда. И получаемые результаты также будут оптимальными далеко не всегда. На практике я метод Циглера-Никольса применял считанное число раз, больше доверяясь экспериментально-аналитическому способу, которому и буде посвящена последующая часть статьи.

Суть метода можно описать максимально кратко:

• Берем систему.
• Меняем один из коэффициентов.
• Смотрим за реакцией системы.
• Анализируем произошедшее и принимаем решение о дальнейших действиях.