2. Открыть эмулятор[1] машины Тьюринга https://cmcmsu.no-ip.info/1course/alg.schema.mt.htm. Изучить примеры.
4. Изучить и выполнить пример 1 стр. 4.
5. Решать задачи стр.5.
Самостоятельная работа.
· Необходимость и способы уточнения понятия алгоритма (символы и слова) [1, стр.27 – 36]
· Машина Тьюринга (структура, такт работы, запись программы, правила выполнения программы, применимость и неприменимость алгоритма к слову, соглашения для сокращения записи программы). Возможности МТ (композиция, разветвление и повторение МТ) Тезис Тьюринга. [2]
· Изучить примеры [2] стр. 7 – 15
· Решить задачи [2] стр. 15 – 18. Тема «Программирование для МТ» войдет в состав контрольной работы.
Литература
1. Кнут Д. Искусство программирования для ЭВМ. Основные алгоритмы: т.1; М.:Мир,2000..
2. Пильщиков В.Н., Абрамов В.Г., Вылиток А.А., Горячая И.В. Машина Тьюринга и алгоритмы Маркова. Решение задач. (Учебно-методическое пособие) — М.: МГУ, 2006. – 47 с.
Машина Тьюринга. Введение. Понятие машины тьюринга. Решение задачи
Структура машины Тьюринга
Машина Тьюринга (МТ) состоит из двух частей – ленты и автомата (головки чтения/записи):

Лента используется для хранения информации. Она бесконечна в обе стороны и разбита на клетки, которые никак не нумеруются и не именуются. В каждой клетке может быть записан один символ или ничего не записано. Содержимое клетки может меняться – в неё можно записать другой символ или стереть находящийся там символ.
Договоримся пустое содержимое клетки называть символом «пусто» и обозначать знаком Λ («лямбда»). В связи с этим изображение ленты, показанное на рисунке справа, такое же, как и на рисунке слева. Данное соглашение удобно тем, что операцию стирания символа в некоторой клетке можно рассматривать как запись в эту клетку символа Λ, поэтому вместо длинной фразы «записать символ в клетку или стереть находящийся там символ» можно говорить просто «записать символ в клетку».
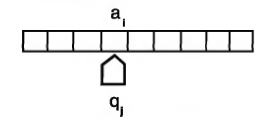
Автомат – это активная часть МТ. В каждый момент он размещается под одной из клеток ленты и видит её содержимое; это видимая клетка, а находящийся в ней символ – видимый символ; содержимое соседних и других клеток автомат не видит. Кроме того, в каждый момент автомат находится в одном из состояний, которые будем обозначать буквой q с номерами: q1, q2 и так далее. Находясь в некотором состоянии, автомат выполняет какую-то определённую операцию (например, перемещается направо по ленте, заменяя все символы b на a), находясь в другом состоянии – другую операцию.
Пару из видимого символа (S) и текущего состояния автомата (q) будем называть конфигурацией, и обозначать .
Автомат может выполнять три элементарных действия:
· записывать в видимую клетку новый символ (менять содержимое других клеток автомат не может);
· сдвигаться на одну клетку влево или вправо («перепрыгивать» сразу через несколько клеток автомат не может);
Конструирование машины Тьюринга
· переходить в новое состояние.
Ничего другого делать автомат не умеет, поэтому все более сложные операции так или иначе должны быть сведены к этим трём элементарным действиям.
Такт работы машины Тьюринга
МТ работает тактами, которые выполняются один за другим. На каждом такте автомат МТ выполняет три следующих действия, причем обязательно в указанном порядке:
записывает некоторый символ S′ в видимую клетку (в частности, может быть записан тот же символ, что и был в ней, тогда содержимое этой клетки не меняется);
сдвигается на одну клетку влево (обозначение – L, от left), либо на одну клетку вправо (обозначение – R, от right), либо остается неподвижным (обозначение – N).
переходит в некоторое состояние q′ (в частности, может остаться в прежнем состоянии).
Формально действия одного такта будем записывать в виде тройки: S′, [L,R,N], q′, где конструкция с квадратными скобками означает возможность записи в этом месте любой из букв L, R или N. Например, такт *,L,q8 означает запись символа * в видимую клетку, сдвиг на одну клетку влево и переход в состояние q8.
Программа для машины Тьюринга
Сама по себе МТ ничего не делает. Для того чтобы заставить её работать, надо написать для неё программу. Эта программа записывается в виде следующей таблицы:

Слева перечисляются все состояния, в которых может находиться автомат, сверху – все символы (в том числе и Λ), которые автомат может видеть на ленте. (Какие именно символы и состояния указывать в таблице – определяет автор программы.) На пересечениях же (в ячейках таблицы) указываются те такты, которые должен выполнить автомат, когда он находится в соответствующем состоянии и видит на ленте соответствующий символ.
В целом таблица определяет действия МТ при всех возможных конфигурациях и тем самым полностью задаёт поведение МТ. Описать алгоритм в виде МТ – значит предъявить такую таблицу.
Замечание. Часто МТ определяют как состоящую из ленты, автомата и программы, поэтому при разных программах получаются разные МТ. Мы же будет считать, в духе современных компьютеров, что МТ одна, но она может выполнять разные программы.
Источник: poisk-ru.ru
Машина Тьюринга, ее структура и свойства. Проблема остановки мт.
Основная гипотеза теории алгоритмов (тезис Тьюринга) – всякий вычислительный процесс может быть преобразован в машину Тьюринга, всякий алгоритм – в таблицу такой машины.
Главное доказательство тезиса Тьюринга – никто и никогда не указал алгоритма, который нельзя было бы преобразовать в машину Тьюринга.
Сам Тьюринг получал свою машину путем анализа работы вычислителя: вычислитель имеет перед собой тетрадь, читает, пишет новые знаки, листает страницы, то есть работает по алгоритму, то есть работает память => ум вычислителя меняет свое состояние.
В машине Тьюринга процесс разложен на элементы(такты). Внутреннее состояние машины – состояние ума вычислителя. Машина Тьюринга – простейшая. Все другие машины и вычислительные модели отличаются от машин Тьюринга укрупнением операций (бегает по памяти, сразу читает и записывает и тп).
Итак, МТ- простейшая идеальная модель вычислительного процесса, а значит и простейшая идеальная вычислительная машина. Вычислительный процесс разложен на элементы. Так как внешняя память бесконечна, то машина не боится переполнения. Реальным машинам будет соответствовать машина Тьюринга с оборванной лентой.
МТ обрабатывает односторонне бесконечную ленту, Лента разбита на клетки, в которых пишутся символы по одному в клетке. Если в клетке ничего нет, то будем говорить, что там записан пустой символ. Множество знаков для ленты машины называется ее внешним алфавитом, в который входит и пустой знак. Внешний алфавит конечен. Машина имеет дискретное время работы. Оно распадается на такты.
В каждый такт она занимает одну клетку ленты, читает записанный там символ, затем записывает новый символ, движется вправо или влево и переходит в следующее внутреннее состояние. Машина имеет конечное множество внутренних состояний (внутренний алфавит машины).
Имеются начальное состояние (с него начинается работа машины) и конечное состояние, попав в которое, машина прекращает работу. Внутреннее состояние машины и воспринимаемый ею символ называется конфигурацией машины. Конфигурация машины однозначно определяет ее дальнейшие действия в этом такте: запись нового знака, движение, переход в следующее внутреннее состояние.
Кроме ленты, имеется головкам чтения/записи, которая, во-первых, умеет двигаться вперед, назад и стоять на месте; во-вторых, умеет читать содержимое, стирать и записывать символы из данного алфавита; в третьих, управляется программой. Программа представляет собой таблицу, в которой в каждой клетке записана команда. Каждая клетка определяется двумя параметрами — символом алфавита и состоянием машины. Команда представляет собой указание, куда передвинуть головку чтения/записи из текущего состояния, какой символ записать в текущую ячейку и в какое состояние перейдет машина.
Более наглядной описание:
Машина Тьюринга состоит из следующих “частей” [2]:
- ленты, разбитой на конечное число ячеек
- Внешней памяти, принимающей одно из состояний, входящих в множество A=a0,a1, …am>. Ячейки ленты находятся в одном и только одном из состояний множества А. Состояние a0 называется пустым.
- Внутренней памяти, принимающей одно из состояний, входящих в множество Q=q0,q1, …qm>. Состояние q0называется “стоп”.
- головки, двигающейся вдоль ленты и считывающей содержимое ячейки, напротив которой она останавливается.
- Механического устройства, передвигающего головку и меняющего состояние внешней и внутренней памяти. Если головка с состоянии q стоит напротив ячейки с номером k, то изменения состояния внутренней памяти и состояния ячейки происходят одновременно.
8(3)
Рис1. Машина Тьюринга.
Работа машины Тьюринга осуществляется посредством команд, которые выполняет механическое устройство. Команда имеет один из следующих трех возможных видов:
qs ai -> qt aj
qs ai -> qt L
qs ai -> qt R
где L – это движение головки влево на одну ячейку, а R – вправо.
Смысл команды таков: если головка в состоянии qs обозревает ячейку в состоянии ai , то в первом случае она меняет свое состоянии на qt , а ячейки на aj , во втором случае — свое состоянии на qt и сдвигается влево, и в третьем – вправо.
Конечный набор команд образует команду.
Состояние машины – это последовательность состояний ai1, … air ячеек ленты, состояние внутренней памяти qs головки и номер k воспринимаемой ячейки в состоянии aik .
Машина Тьюринга работает на неограниченной с обеих сторон ленте, разделённой на ячейки, одну из которых обозревает головка. В любой момент времени все ячейки, кроме конечного числа, заняты пустыми символами. Конфигурацией машины Тьюринга m называется слово вида αqixβ, где — α и β непустая часть ленты, qi — текущее состояние управляющего устройства, x — обозреваемый головкой символ.
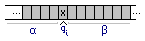
Рисунок 1 — Машина Тьюринга в состоянии qi , конфигурация αqixβ.
За каждый такт работы машины Тьюринга головка считывает обозреваемый символ с ленты и записывает на его место новый, при этом машина переходит в новое состяние qj или остаётся в старом, а головка передвигается на одну позицию влево или вправо, либо остаётся на месте. Порядок работы машины Тьюринга обычно записывается в виде таблицы, где в каждый столбец первой строки заносится возможное состояние машины Тьюринга qi Є Q, а в каждую строку первого столбца заносится символ внешнего алфавита x Є T.
В других ячейках записываются команды исполняемые машиной Тьюринга в состоянии qi при обозревании символа x (ячейка пуста, если предполагается, что символ x не встречается в состоянии qi). Формат команды задаётся тройкой aKq, где а — символ печатаемый на ленте, К — направление движения головки из , q — новое состояние машины Тьюринга.
Рассмотрим программу сложения двух чисел заданных на ленте в унарной системе счисления для машины Тьюринга. Программа принимает 2 числа разделённых символом разделителя (‘*’), и записывает результат их сложения на ленте сразу за этими числами отделяя его символом ‘=’. Начальное состояние машины Тьюринга — q0, а головка обозревает первый символ первого числа. Конечное состояние — qz, при этом головка возвращается к исходной позиции. Программа перед своим завершением должна восстановить исходные данные на ленте.
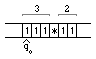
8(4)
Рисунок 2 — Пример начального состояния машины Тьюринга
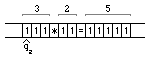
Рисунок 3 — Пример конечного состояния машины Тьюринга
Итак, внешний алфавит для решения данной задачи представляет из себя множество T = λ, 1, 0, *, =>, а программа выглядит следующим образом:
Источник: studfile.net
Примеры машин Тьюринга
Рассмотрим машины Тьюринга, реализующие и обеспечивающие формирование рекурсивных функций.
Пример 1. Построить машину Тьюринга, вычисляющую функцию .
Пусть алфавит машины Тьюринга состоит из двух символов , где 0 – пустой символ, а 1 – символ занятой ячейки. В этом алфавите любое целое неотрицательное число k представляется k+1 символами 1, записанными в соседних ячейках ленты. В этом случая число 0 будет записано так …010…
Определим порядок вычисления значения этой функции машиной Тьюринга. Так как результат должен представлять массив из занятых ячеек, где — число ячеек, занятых аргументом x, то вычисление организуем следующим образом. В ячейку, занятую аргументом x, вместо символа 1 записываем пустой символ 0. В каждом таком случае символ 1 записывается в двух ячейках, представляющих результат. Этот результат формируем в виде массива ячеек, расположенных справа от массива ячеек, занятых аргументом x, через одну пустую ячейку. Когда вместо всех ячеек, занятых аргументом x, будут только пустые ячейки, в новом массиве занятых ячеек удаляется одна ячейка с символом 1.
Программа работы машины Тьюринга, вычисляющая функцию , имеет вид:
— удалена одна занятая ячейка аргумента.
— читаются занятые ячейки аргумента.
— найдена разделяющая пустая ячейка.
— читаются занятые ячейки результата.
— заполнена одна пустая ячейка результата.
— заполнена вторая ячейка результата.
— просматриваются в обратном порядке занятые ячейки результата.
— найдена пустая разделяющая ячейка.
— найдена вторая пустая ячейка.
— снова читается пустая разделительная ячейка.
— удаляется один занятый символ. Конец.
— найдена занятая ячейка аргумента.
— просматриваются в обратном порядке занятые ячейки аргумента.
— найдена пустая ячейка перед занятыми ячейками аргумента.
Пример 2. Построить машину Тьюринга, применимую ко всем словам в алфавите < a, b > и переводящую их в слово . Проверить работу построенной машины над некоторыми словами.
Решение. Опишем работу алгоритма, решающего эту задачу. Вначале с помощью команд , проходим до конца слова, не изменяя его символов. Признаком окончания слова будем считывание символа в состоянии .
С помощью команд , , движемся влево, не изменяя последнего символа.
Если в состоянии считываем символ a, значит, , надо стирать все символы слова , кроме последнего. Это можно сделать с помощью команд , , .
Если в состоянии считывается символ , значит, вся работа проделана, и пора останавливаться с помощью команды .
Если в состоянии считываем символ b, значит, , надо все символы, кроме , заменить буквами b. Это делаем с помощью команд , , .
Если в состоянии считываем символ , значит, все символы исходного слова пройдены, можно переходить в состояние с помощью команды .
Проверим работу построенной машины Тьюринга над словом abba:
| abba, | abba, | abba, | abba, | abbal, | abba, | abba, | abba, |
| lbbba, | lbbba. |
Итак, в слове abba предпоследний символ — b, и все буквы исходного слова, кроме последнего, заменены буквой b.
Проверим работу построенной машины Тьюринга над словом bbaaa:
| bbaaa | bbaaa | bbaaa | bbaaa | bbaaa | bbaaal | bbaaa |
| bbaaa | bbala | bblla | bllla | llllla | llllla |
В слове bbaaa предпоследний символ — a, и все буквы исходного слова, кроме последнего, заменены пустыми символами .
Итак, проверка сделана, результат работы машины Тьюринга удовлетворяет требованиям, которые ставились в условии задачи.
В приведенных примерах показана реализуемость на машинах Тьюринга основных свойств алгоритма: дискретности, детерминированности, массовости и результативности.
Чтобы можно было строить сложные машины Тьюринга, определяют понятие композиции машин Тьюринга.
Композицией машин Тьюринга М1 и М2 называется машина Тьюринга М, которая первоначально функционирует как машина Тьюринга М1, заключительное состояние которой q 0 изменяют на начальное состояние машины Тьюринга М2. И далее машина М функционирует как машина Тьюринга М2.
Композицию машин Тьюринга обозначают: М = М1 º М2.
Из определения композиции машин Тьюринга следует, что М1 º М2 ≠ М2 º М1.
Так, если необходимо построить машину Тьюринга, вычисляющую функцию ƒ(х, у) = х + у + 1, то достаточно выполнить композицию машин Тьюринга. Пусть машина М1 вычисляет функцию ƒ(х) = х + 1, а машина М2 вычисляет функцию ƒ(х + у). Тогда машина М = М1 º М2 будет вычислять, очевидно, функцию ƒ(х, у) = х + у + 1. Для этого нужно к программе, описывающей машину М1, присоединить команды машины М2. Состояния машины М1 будут также состояниями машины М. Заключительное состояние q 0 машины М1 следует заменить состоянием q 2,которое будет соответствовать начальному состоянию машины М2. тогда изменится соответствующим образом нумерация состояний машины М2: состояние q 1 изменится на состояние q 2 машины М, состояние q 2 изменится на состояние q 3 и так далее.
Существует много модификаций машин Тьюринга, среди которых можно выделить универсальные и многоленточные машины. Для универсальных машин характерно одновременное использование правой и левой полулент, на одной из которых записываются все команды для вычисления заданной функции, а на другой все текущие конфигурации.
Для многоленточных машин характерно наличие нескольких лент и нескольких головок, что позволяет организовать одновременную работу согласно протоколу на всех лентах, что удобно при организации сложных параллельных вычислений.
Рекурсивные функции и машины Тьюринга дают косвенное определение понятие алгоритма: если возможно доказать, что некоторая функция примитивно-рекурсивна, или возможно построение машины Тьюринга для получения решения некоторой задачи, то такая задача разрешима.
С другой стороны, если доказано, что решение некоторой задачи не может быть получено вычисление примитивно-рекурсивных функций, или доказано, что для решения данной задачи не может быть построена машина Тьюринга, то такая задача называется алгоритмически неразрешимой.
Важность доказательства факта, что некоторая задача алгоритмически неразрешима, состоит в том, что исследователь не будет тратить время и силы на разработку алгоритма решения данной задачи в общем виде.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник: studopedia.ru