Для формирования навыков записи алгоритмов с использованием базовых управляющих команд организации действий можно использовать алгоритмические стихи (алгостихи), т.е. стихотворения, по содержанию представляющие некоторый алгоритм.
Рассмотрим пример алгостиха, который можно интерпретировать основными управляющими командами.
Стихотворение «Царица мух», Н.Заболоцкий
Если ты, мечтой томим,
Знаешь слово Элоим 8 ,
Муху странную бери,
Муху в банку посади,
С банкой по полю ходи,
За приметами следи.
Если муха чуть шумит,
Под ногою медь лежит.
Если усиком ведет,
К серебру тебя зовет.
Если хлопает крылом,
Под ногами злата ком.
Из истории создания стихотворения «Царица Мух»
Н. Заболоцкий (1903-1958 гг.) так пишет об истории создания этого стихотворения.
Знаменитый ученый Агниппа Ноттенгеймский Генрих Корнелий (1486-1535 гг.) – разносторонний ученый, царицей мух называет какую-то таинственную муху, величиной с крупного шмеля, которая любит садиться на водяное растение, называемое Pluteau plantagine, и с помощью которой индусы якобы отыскивают клады на своей родине. Когда вы имеете в своем распоряжении одну из таких мух – посадите ее в прозрачный ящичек.
Курс по смарт-контрактам. Виртуальные машины в блокчейне
Её помещение надо освежать 2 раза в день и давать ей растение, на котором ее поймали. Она может жить в таких условиях почти месяц. Чтобы узнать направление скрытых на известной глубине сокровищ, надо, чтобы стояла хорошая установившаяся погода. Тогда, взяв ящичек с мухой, отправляйтесь в путь, постоянно посматривая и подмечая ее движения.
Когда вы будете находиться над местом, содержащим золото или серебро, муха замахает крыльями, и чем ближе вы будете, тем сильнее будут ее движения. Если в недрах сокрыты драгоценные камни, вы заметите содрогания в лапках и усиках. В том же случае, если там находятся лишь неблагородные металлы, как медь, железо, свинец и пр., муха будет ходить спокойно, но чем быстрее, тем ближе к поверхности они находятся. Нечто похожее на это предание можно услышать и в русских деревнях.
Блок-схема1 алгоритма «Царица мух»
Для составления блок-схемы1 использовано вложенное ветвление.
Б лок-схема2 алгоритма «Царица мух»
Для составления блок-схемы2 использована команда выбора в неполной форме.
5. Алгоритмы для исполнителя мнр (машины с неограниченными регистрами)
Опишем исполнителя МНР. МНР состоит из памяти данных и программной памяти. Ячейки памяти данных называют регистрами и обозначают R0, R1, R2 и т.д. до бесконечности. В каждом регистре может содержаться любое целое неотрицательное число. Число, содержащееся в Rn, или значение регистра Rn будем обозначать rn.
В каждый момент времени только конечное число регистров содержит какие-то числа, т.е. память данных является не бесконечной, а потенциально бесконечной. МНР работает по программе. Программой называется пронумерованная конечная последовательность команд, хранящаяся в программной памяти. Программная память МНР также является потенциально бесконечной. Будем считать, что во всех ячейках, свободных от команд программы записана специфическая команда – Stop, результатом исполнения которой является остановка выполнения программы.
Лекція 3. Машина Тюрінга. Поняття машини Тюрінга. Розв’язання задачі
Система команд МНР содержит следующие команды:
1. Команда обнуления.
Команда обнуления записывается Z(n). Команда Z(n) выполняется так: содержимое регистра Rn обнуляется, т.е. rn становится равным нулю (rn:=0), содержимое других регистров не изменяется.
Пример 5. Пусть начальная конфигурация МНР имеет вид:
2. Команда прибавления единицы.
Команда прибавления единицы имеет вид S(n). Команда S(n) выполняется так: содержимое регистра Rn увеличивается на единицу, т.е. rn:=rn+1, новое значение rn равно старому значению, сложенному с 1, содержимое других регистров не изменяется.
Пример 6. Пусть начальная конфигурация МНР имеет вид (). МНР выполнит команду S(4). Тогда новая конфигурация имеет вид:
3. Команда переадресации.
Команда переадресации имеет вид T(m,n). Команда T(m,n) выполняется так: содержимое регистра Rn заменяется числом rm, содержащимся в регистре Rm, т.е. rn:=rm, содержимое других регистров (включая Rm) не изменяется.
Пример 7. Пусть начальная конфигурация МНР имеет вид (). МНР выполнит команду T(4,2). Тогда новая конфигурация МНР имеет вид:
В МНР есть особый регистр, который назовем счетчиком адресов команд (САК). При запуске программы на выполнение в САК заносится 1. Выполнение каждой команды МНР состоит из четырех этапов:
1. Читается адрес из САК.
2. Запоминается команда из памяти по этому адресу.
3. САК увеличивается на единицу.
4. Выполняется запомненная команда.
МНР выполняет каждую команду программы в 4 этапа, пока не встретит команду Stop.
Команды обнуления, прибавления единицы и переадресации называются арифметическими. После каждой команды типа 1-3 выполняется команда со следующим номером.
4. Команда условного перехода.
В работе алгоритма могут быть моменты, когда предписываются альтернативные действия, зависящие от результата работы алгоритма к этому моменту. В других ситуациях может потребоваться повторить группу команд несколько раз. МНР может выполнять такие процедуры, используя команды условного перехода; они позволяют делать скачки вперед и назад в списке команд. Мы будем использовать команду условного перехода для совершения, например, следующего действия: «Если r2=r6, перейди к десятой команде программы, в противном случае, перейди к следующей команде программы». Команда, вызывающая это действие, записывается как J(2,6,10).
Команда условного перехода в общем виде записывается так J(m,n,q). Выполнение команды осуществляется следующим образом: сравнивается содержимое регистров Rm и Rn, если rm=rn, то МНР переходит к выполнению q-ой команды исполняемой программы, в САК заносится число q; если rmrn, то МНР переходит к выполнению команды, следующей в программе за J(m,n,q), САК увеличивается на единицу, содержимое регистров не изменяется. Если условный переход невозможен ввиду того, что в исполняемой программе команд меньше, чем q, то МНР прекращает работу.
С помощью данной команды можно осуществлять и безусловный переход. Для этого команду нужно записать следующим образом: J(m,m,q).
Работа на МНР состоит из следующих этапов:
1. Заполняем регистры памяти данных какими-то числами, т.е. задаем так называемую начальную конфигурацию.
2. Заполняем командами ячейки программной памяти.
3. Записываем в САК единицу, запускаем МНР и она работает так, как было описано выше до тех пор, пока не встретит команду Stop. При этом полученное по окончании работы машины содержимое регистров памяти данных называется конечной конфигурацией.
Примеры алгоритмов
Задача 37. Напишите для исполнителя МНР алгоритм вычисления суммы целых положительных чисел x и y, результат запишите в регистр R0.
Решение. Поместим x в регистр R0, y – в регистр R1, т.е. зададим начальную конфигурацию:
Источник: studfile.net
Вычисление функций на машинах с неограниченными ресурсами.
Как и в случае машин Тьюринга, мы должны указать, как машина с неограниченными регистрами вычисляет частичную функцию f(x1,x2. xn) от n аргументов. Рассмотрим набор аргументов (x1,x2. xn) и разместим число x1 в регистре R1, число x2 – в регистре R2. число xn — в регистре Rn. Все остальные регистры заполнены нулями. Получаем начальную конфигурацию МНР.
После окончания работы в регистре R1 должно быть значение функции f(x1,x2. xn). Если значение f(x1,x2. xn) не определено, то МНР должна работать бесконечно.
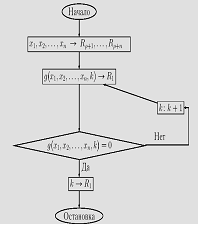
72)Вычислимость простейших функций на машинах с неограниченными ресурсами. Теорема. Простейшие функции s(x)=x+1, on(x1,x2. xn)=0, In
m(x1,x2. xn)=xm вычислимы на МНР. Доказательство. Укажем программы для вычисления данных функций. 1) Функция следования s(x) имеет программу из одной команды S(1). Действительно, если в регистре R1
занесено число x, то МНР выполнит один такт работы, сменит число x в R1 на число x+1 и остановится. 2) Аналогично программа, состоящая из одной команды Z(1), вычисляет нулевую функцию on(x1,x2. xn)=0.3) Для функции проектирования In m(x1,x2. xn)=xm применяем программу из одной команды T(m,1). МНР выполнит один такт работы, перешлет в регистр R1 число xm и остановится. Теорема доказана.
Итак, все простейшие функции из определения частично рекурсивной функции вычислимы на МНР. Далее установим, что все частично рекурсивные функции вычислимы на МНР.
73)Стандартный вид программы. Сложная программа часто содержит другие программы в качестве строительных блоков — подпрограмм. Для правильного взаимодействия этих подпрограмм нужно соблюдать некоторые
правила. Определение. Пусть дана программа для МНР, состоящая из s команд. Будем говорить, что программа имеет стандартный вид, если во всякой команде условного перехода J(m,n,q) данной программы выполняется неравенство q s + 1. Если программа P не имеет стандартного вида, то в ней найдется команда вида J(m, n, q), где q > s+1. Заменим в программе P эту
команду на команду J(m,n, s + 1). Получим программу P’’, выполняющую точно такое же действие, как и программа P. Действительно, P и P’ отличаются лишь командами J(m, n, q) и J(m,n, s + 1). Однако действие этих команд одинаково: при rm rn нужно перейти к следующей по порядку команде, а при rm = rn остановиться.
Определение.Стандартизацией программы I1, I2, …,Is называется замена в данной программе всех команд J(m, n, q) где q > s+1, на команды J(m, n, s + 1). В результате стандартизации из программы P нестандартного вида получим стандартную программу P’ с тем же действием. Используя P’ вместо P, считаем, что все программы, которые мы рассматриваем, стандартны.
74) Соединение программ. Определение. Соединением программ P: I1, I2. Is и Q: I’1, I’2. I’t называется программа из s+t команд вида I1, I2. Is, Is+1, Is+2.
Is+t, где команды Is+1, Is+2. Is+t получены из команд I’1, I’2. I’t программы Q приращением номеров на число s. При этом каждая команда условного перехода J(m, n, q) из Q заменена на команду вида J(m, n, q+s). Соединение программ P и Q будем обозначать через PQ. Можно соединить программы P, Q, R и получить программу PQR=(PQ)R и т.д.
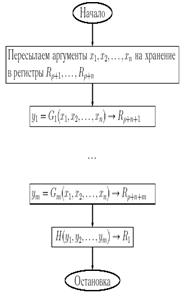
75) Вставка подпрограммы. Пусть в программе Q имеется подпрограмма P для вычисления функции f (x1,x2. xn). В подпрограмме P имеются входные данные (x1,x2. xn) и результат вычислений f (x1,x2. xn). По определению МНР должны соблюдаться следующие требования. 1. При старте P аргументы (x1,x2. xn) обязаны находиться в регистрах R1.
Rn..
2. После окончания работы подпрограммы P результат f (x1,x2. xn) должен содержаться в регистре R. Однако в ходе работы основной программы Q возможно следующее. Настал момент для старта подпрограммы P, которой нужны аргументы x1, x2. xn. В данный момент аргументы хранятся в каких-то регистрах Ri1. Rin, а не в регистрах R1. Rn, как нужно.
Поэтому перед применением подпрограммы P мы должны извлечь аргументы из Ri1. Rin и переслать их в регистры R1. Rn такой пересылки аргументов выполняется следующее действие. 1) Перед командами из P размещается набор команд T(i1,1). T(in,n). Пусть основная программа Q вызвала подпрограмму P и в начало зарезервированных регистров R1.
Rn скопированы числа x1, x2. xn, с которыми начнет работать подпрограмма P. Однако в регистрах Rn+1.
R может оставаться «мусор» — произвольные числа, оставшиеся от предыдущей работы Q. По правилам работы МНР в последующих регистрах Rn+1. Rk должны быть только одни нули. Поэтому нужно выполнить обнуление этих регистров от мусора, которое осуществляется следующим способом. 2) Выполняется набор команд Z(n+1). Z().В итоге в основной программе получается следующий фрагмент T(i1,1).
T(in,n) Z(n+1). Z() PT(1,i) Вставку данного фрагмента в основную программу обозначаем
76) Вычислимость частично рекурсивных функций на МНР. Если функция f вычислима на некотороймашине с неограниченными регистрами, тоговорим кратко «Функция f МНР вычислима».В предыдущей лекции установлена МНРвычислимость простейших функций. Теперьпроверим, что применение операторовсуперпозиции, примитивной рекурсии иминимизации к МНР вычислимым функциямвырабатывает МНР вычислимые функции. Врезультате получим основной результат -все частично рекурсивные функции вычислимы
77) Оператор суперпозиции. Теорема 1. Пусть функция f получена из
функций h, g1, g2, …, gm с помощью оператора суперпозиции. Если функции h, g1, g2, …, gm МНР вычислимы, то и функция f также МНР вычислима. Доказательство. По условию функции h, g1, g2, …, gm МНР вычислимы. Пусть H, G1, G2, …, Gm- программы, вычисляющие эти функции.
78) Оператор примитивной рекурсии. Теорема 2. Пусть функция f получена с помощью операторапримитивной рекурсии из функций g и h. Если функции g и hМНР вычислимы, то и функция f также МНР вычислима.
Доказательство. По условию функции g и h МНР вычислимы. Пусть G и H программы, вычисляющие эти функции. Выразим кратко процесс вычисления функции f = f(x1, x2. xn, y). Сравниваем y с числом 0. Если равенство верно, то вычисляем f(x1, x2. xn, 0) = g(x1, x2. xn)
и останавливаемся. В противном случае несколько раз применяем программу H для последовательного вычисления чисел f(x1, x2. xn, k) при k=0, 1. y.
79)Оператор минимизации. Алгоритм вычислений. ► Теорема 3. Пусть функция f получена из функции g с помощью оператора минимизации. Если функция g является МНР вычислимой, то и функция f также МНР
вычислима. Доказательство. Построим программу, вычисляющую функцию f. Пусть G – программа, вычисляющая функцию g. Будем считать, что программа G приведена к стандартному виду. Искомая программа для функции f будет проверять одно за другим следующие равенства: g(x1,x2. xn,0)=0,
g(x1,x2. xn,y)=0, стремясь найти наименьшее k с условием
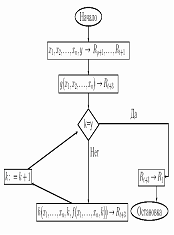
80) Программа вычисления. T(1,p+1)
IqT(p+n+1, 1) При этом команда Ip является первой командой
подпрограммы G[p+1, p+2. p+n+11].
Работа программы Пусть p=max(n+1, p(G)). Распределимпамять: Регистры R1. Rp предназначены дляработы подпрограммы G.В регистрах Rp+1. Rp+n постояннохранятся аргументы x1. xn.В регистр Rp+n+1 будет записыватьсячисло k.В итоге получим искомое число k или машина будет работать бесконечно, что означает, что функция f(x1, x2. xn) не существует. Теорема доказана.
81) Нормальные алгорифмы. • Третий вариант формализации понятия алгоритма предложен российским мaтематикомА.А.Марковым.• В этом определении считается, что алгоритмический процесс – это процесс переработки слов некоторого алфавита. Алфавит нормальногоалгорифма A — это некоторая конечная совокупность символов A = . Элементы из A мы будем называть буквами. Из букв алфавита A составляются слова —
конструктивные объекты, которые поступают на вход и перерабатываются в
алгорифме A. При этом говорят, что A — алгорифм в алфавите A. Схема нормального алгорифма Рассмотрим две буквы и , которые не входят в алфавит A. Формулой подстановки назовем выражение u v или выражение u v, где u и v — произвольные слова в алфавите A. Формула без точки называется простой формулой, а формула с точкой называется заключительной формулой. В обоих случаях формула имеет левую часть u и правую часть v, которые должны быть словами в алфавите A. Знаки и могут быть любыми буквами вне алфавита A. Мы могли вместо них
использовать, например, греческие буквы и .
82) Алгоритм сложения натуральных чисел. Построим нормальныйалгорифм, вычисляющий сумму двух натуральных чисел x и y. Для этого рассмотрим алфавит из трех символов A=. Число n N изображаем словом 0||. | в алфавите A. В этом слове n палочек, перед которыми
поставлен символ 0. Искомый нормальный алгорифм A имеет схему из одной
заключительной формулы подстановки u1 v1, где u1 = +0 — слово из
двух букв, а v1 = — пустое слово. Тем самым схема алгорифма имеет вид
+0 Если нужно вычислить сумму x+y, то подаем на вход алгорифма A ее
изображение, т.е. словоP=0||. |+0||. | Алгоритм A удалит из P подслово +0 и в один шаг переработает входное слово P в выходное слово Q. При этом
83) Принцип нормализации Маркова. Сделаем несколько предварительных замечаний. Не все вербальные алгорифмы являются нормальными алгорифмами,такткак вербальные алгорифмы реализуют произвольные преобразования слов, а нормальные алгорифмы ограничены
преобразованиями слов по заданной схеме. Поэтому определение алгоритма по Маркову не будет утверждать о совпадении класса нормальныхалгорифмов и класса вербальных алгорифмов, а будет иметь другую формулировку. Рассмотрим эту формулировку. Пусть задан алфавит A. Добавим к алфавиту A новые буквы. Получим алфавит A1 с условием AA1.
Алфавит A1 называется расширением алфавита A. Нормальныйалгорифм в каком-либо расширении A1 алфавита A называется нормальным алгорифмом над алфавитом A. А.А.Марков предложил следующий тезис. Принцип нормализации. Пусть задан произвольный вербальный алгорифм A в алфавите A. Тогда существует расширение A1 алфавита A и нормальныйалгорифм A1 в алфавите A1 с условием: произвольное слово P в алфавите A
перерабатывается нормальнымалгорифмом A1 в тот же самый результат, в который слово P перерабатывается исходным вербальным алгорифмом A.Поэтому принцип нормализации можно рассматривать как способ обозрения всевозможных действий в вербальных алгоритмах. Поскольку эти действия строго заданы, то мы имеем третий вариант определения алгоритма. В результате принятия принципа нормализации мы получили инструмент для доказательства неосуществимости задачи нахождения определенного алгоритма. Доказано, что данная формулировка понятия алгоритма (принцип
нормализации) эквивалентна другим формулировкам понятия алгоритма: тезису Черча, использующему частично рекурсивные функции, и тезису Тьюринга, использующему понятие вычислительной машины. Поэтому еще раз подкрепляется уверенность в том, что мы нашли и выразили в трех формах фундаментальное понятие математики, логики и информатики — понятие алгоритма. При этом частичная рекурсивность, машина Тьюринга, МНР и нормальныйалгорифм — лишь различные формы выражения этого самостоятельного понятия.
Источник: poisk-ru.ru
Лекции — Теория алгоритмов

содержит ч исла, о тличные от нуля . Все остальные регистры з аполнены нулями.

(продолжение)
► 2) Программа машины – это конеч ная последова тельность I
следу ющих четы рех типов команд:
Z(n), S(n), T(m, n ), J( m, n, q),
где m, n, q <1,2, . >. Эти ко манды вы полняют следу ющие дейст вия.
► Ко манда обнуления Z(n ) дела ет содержимое регистра R
равным нулю.
► Ко манда при бавления единицы S(n) к содержимому регистра R
прибавляет число
► Ко манда переадресации T(m, n) заменяет соде ржимое регистра R
на со держимое
регистра R
► Ко манда условного перехода J( m, n, q) сравнивает содержимое ре гистров R
в каче стве следу ющей ко манды вы полняется команда с номером q,
в противном слу чае выпо лняется след ующая по поря дку к оманда программы.
► Ко манды обнуления, прибавления ед иницы и переадресац ии называются
арифметиче скими командами.

Примеры выполнения команд
► Пусть, например, регистры МНР имеют
► Выполним команду S(2). Эта команда
прибавит 1 к числу 3 в регистре R
затронет остальные регистры. В
результате п олучим следующее
содержимое регистров

(продолжение)
► Выполним зате м команду T(2,1). Содержимое 4
из ре гистра R
заменит старо е содержимое 2 в
регист ре R
. Получим регистры
► Машина с нео граниченными регистрами, как и
произ вольны й алгори тм, работает по тактам:
такт 1, такт 2, … . Первый так т работы МНР с
прог раммой I
— выполне ние первой
. Затем выполняются команды I

Условие остановки
► Машина остана влива ется тогда и только тогда, когда
невозможно выполни ть очередную предписа нную
коман ду. Это озна ча ет, что МНР только что совершила
i- вый такт ра боты и следующим i+1 тактом дол жна
вып олнить несуществующую команду. Эта ситуа ция при
выполнен ии программы I
возни кает ровн о в
одном и з трех следующих случа ев.
► I) Если в i — во м такте в ыполнен а I
команда про граммы и э та команда не является
коман дой условн ого перехода, тогда следующим i+1
тактом должна в ыполняться несуществующая команда

( продо лж ение )
► 2) Если в i — вом такте выполнена команда
условного пере хода J(m, k , q), где r
Источник: www.studmed.ru