Программа для исследование функции и построение ее графика

Цель работы – показать алгоритм построение графиков функций в Excel, принцип построения линий высших порядков в полярной системе координат с помощью формул перехода от декартовых координат к полярным координатам.

Использование компьютерных программ для построения графиков функций, изучение их свойств и закономерностей, дает возможность рассмотреть большое количество примеров с минимальными усилиями. Данная работа предназначена в помощь учителям при изучении функции, а также ученикам с целью заинтересовать их математикой, информатикой, показав возможности использования информационных технологий на уроках математики.

Скачать:

Предварительный просмотр:

«Р айонная научно-практическая конференция

«От исследования — к научному поиску»

Учреждение: МБОУ «Многопрофильная гимназия г. Лагани»

«Построение и исследование графиков

Математика без Ху%!ни. Исследование функции, график. Первая, вторая производная, асимптоты.

функций при помощи электронных

Автор работы: Белкин Алексей Васильевич ,

ученик 10 класса МБОУ «Многопрофильная гимназия г. Лагани»

Научный руководитель: Никифоров Евгений Алексеевич,

учитель математики МБОУ «Многопрофильная гимназия г. Лагани»

1. Инструкция по построению кривых с помощью программы

1.2. Полярная система координат

1.3. Инструкция по построению кривых в полярных координатах с помощью программы Microsoft Excel

1.4. Построение кусочно-заданной функции на примере построения эскиза национального орнамента

Актуальность работы. При изучении, темы преобразования графиков функций возникла необходимость построения графиков элементарных функций и уравнений выше второй степени. Для изучения свойств этих функций Microsoft Excel предлагает широкие возможности, которые в школьных учебниках по информатике не оговариваются.

Вопрос (мотивация ): Как построить график с изменяющимся параметром, для дальнейшего его изучения?

Проблема: необходимо найти удобный (сравнительно простой, наглядный, доступный) способ построения графиков элементарных функций и уравнений степеней выше второй с двумя переменными.

Гипотеза: для решения поставленной проблемы, возможно использовать инструменты прикладной программы Microsoft Excel, а для построения графиков уравнений высших порядков ввести новые переменные, или новую систему координат, или и то и другое одновременно.

Поэтому, объект нашего исследования — прикладная программа Microsoft Excel, ее возможности для построений графиков функций и исследования их .

Исходя из этого, предметом нашего исследования стали уравнения элементарных функций и кривых высших порядков.

Цель работы – показать алгоритм построение графиков функций в Excel, принцип построения линий высших порядков в полярной системе координат с помощью формул перехода от декартовых координат к полярным координатам. Результаты исследования: в процессе работы я:

Математический анализ, 16 урок, Исследование функции и построение графика

• Научился строить графики функций, с дальнейшей возможностью изучения их свойств
• изучил переход от декартовой системы координат к полярной и обратно;
• исследовал изменения вида графиков функций и кривых, в зависимости от параметров входящих в её уравнение;
• познакомились с некоторыми замечательными кривыми известных математиков.

Планы и перспективы: продолжить изучение плоских кривых.

1. Инструкция по построению кривых с помощью программы

Пусть задана функция y= f(x), где х – независимая переменная , а y – переменная зависящая от х.

Для начала нам необходимо задать значения независимой переменной с заданным шагом (шаг лучше выбрать дробным значением). Чем меньше шаг вычисления независимой переменной тем точнее построенный график.

Задаем формулу по которой определяется зависимая переменная. Вычисляем для каждого значения независимой переменной ее соответствующее значение функции.

По построенным данным строим график функции.

Следовательно, математическая модель у нас уже есть. Рассмотрим пример построения уравнения графика и ее исследования

. Рассмотрим в качестве примера тригонометрическую функцию

Построим компьютерную модель исследования.

Для дальнейших исследований будем одновременно строить график исходной элементарной функции y= sinx и преобразованной функции и сравнивать полученные результаты.

Формулы будут записаны в терминах электронных таблиц следующим образом:

А3= -7
А4 =А3+0,1 (шаг можно уменьшить например до 0,001)
B3 =sin(a3)
у меня независимая переменна изменяется на интервале (-7;7), что примерно соответствует интервалу ( )

В ячейке F1 будем задавать значение параметра k, и рассматривать полученные изменения графика функции

Фрагмент произведенных расчетов из электронной таблицы приведен ниже

В приложенном к работе файле Microsoft Excel работа графики можно увидеть полные вычисления и полученные результаты

Для детального изучения преобразований графики построил в одной системе координат, что дает возможность сравнить полученные результаты.

Для дальнейших исследований достаточно теперь изменить значение в ячейке f1, и получим иную картину. Например f1=-4

Как видно значения функции автоматически пересчитаны, и построен уже другой график. Данные возможности мною были продемонстрированы одноклассникам на уроке математики. В дальнейшем мои товарищи на уроки изучили свойства полученных графиков функций и наглядно изучили преобразования графиков следующих функций

1.2. Полярная система координат.

Мои исследования, на этом не закончились, возник вопрос в построении более сложных графиков. В качестве примера мною рассмотрено уравнение

В полярной системе координат положение точки определяется полярным радиусом R и углом , образуемым полярным радиусом с полярной осью. Следовательно, полярная система координат — система координат, ставящая в соответствие каждой точке на плоскости пару чисел . Основными понятиями этой системы являются точка отсчёта (полюс) и луч, начинающийся в этой точке (полярная ось).

Если в декартовой системе координат предельно простое выражение определяет прямую линию, то это же выражение, переписанное в форме , уже превращается в спираль. Фигуры в полярных координатах образуются как след конца бегающего по кругу полярного радиуса переменной длины. Длина полярного радиуса определяется величиной угла, который в данный момент времени он образует с полярной осью. Координата берётся со знаком «+», если угол от оси до отрезка вычисляется против часовой стрелки, и со знаком «-» в противоположном случае. Любая точка в этой системе имеет бесконечное число координат вида , которым соответствует одна и та же точка при любых натуральных . Для полюса , угол произвольный.

Связь между полярной и декартовой системами координат.

Точка О — полярный полюс , луч ОЕ будем называть полярной осью , отрезок ОМ — называют длиной полярного радиуса R , п оложительный угол от луча ОЕ до луча F — полярный угол .

Если известны полярные координаты R и , точки М , то можно уставить связь с её декартовыми координатами.

Построим прямоугольный ОМЕ . В этом треугольнике гипотенуза ОМ = R , ЕОМ = , катет ЕМ = у , катет ОЕ = х координаты точки М .

Для того, чтобы перейти от полярных координат к декартовой системе, используют формулы: , , . Обратно, чтобы, имея прямоугольные координаты, получить расстояние нужное для задания полярных координат, надо воспользоваться теоремой Пифагора: , затем , .

Некоторые замечательные кривые. На протяжении многих лет ученые собирали информацию о формулах, рисующих разные фигуры. Многие фигуры получили свои названия. Список таких названий внушителен: спираль Архимеда, Ферма, Галлилея, Фибоначчи, кардиоида, овалы Кассини, лемниската Бернулли, фигуры Лиссажу, розы Гвидо Гранди, кривые Маклорена, верзьера (локон Марии Аньези) и т.д.

1.3. Инструкция по построению кривых

в полярных координатахс помощью программы Microsoft Excel.

Если уравнение задано в декартовых координатах, то следует перевести его в полярные, используя формулы: X=R*COS(F), Y=R*SIN(F). Следовательно, математическая модель у нас уже есть. Рассмотрим пример построения кривой.

Задача. Построить кривую, заданную уравнением .

Решение. Найдем уравнение данной линии в полярных координатах.

Для программы Microsoft Excel: R=4*COS(3*F)

Предположим, что угол F изменяется в интервалах от 0 до 2 . Для того, чтобы построить эту кривую наиболее точно, с малым шагом изменения угла F, как мы это делали при построении тригонометрических функций, мы выберем шаг изменения 0,1.

Построим компьютерную модель исследования.

Формулы будут записаны в терминах электронных таблиц следующим образом:

А2 0,1 А3 =А2+0,1 B2 =4*COS(3*F)
C2 =SIN(А2) D2 =COS(А2) E2 =B2*D2 F2 =В2*C2

Тогда получаем следующее распределение по столбцам электронной таблицы:

Для построения графика выделим информационный блок E2..F64, так как аргумент F, будем изменять от 0,1 до 6,3 радиана. Возможно изменение и до 9,42, 12,56, и т. д. Получим следующий график.

Исследование формы кривой , в зависимости от изменения значений входящих в её уравнение. Внося изменения в ячейку H27 , не меняя более ничего, мы можем получать различные виды уравнения

Обратимся к исследованию формы роз. Поскольку правая часть уравнения не может превышать величины a , то и вся роза, очевидно, уменьшается внутри круга радиусом a . Количество же лепестков розы зависит от величины модуля k :

1. Если модуль k – целое число, то роза состоит из k лепестков, при нечетном k , и из 2 k лепестков при k четном.

2.Если модуль k – рациональное число, равное то роза состоит из m лепестков в случае, когда оба числа m и n нечетные, и из 2 m лепестков, если одно из этих чисел является четным.

При этом, в отличие от первого случая каждый следующий лепесток будет частично перекрывать предыдущий.

3.Если модуль k – иррациональное число, то роза состоит из бесчисленного множества лепестков, частично накладывающихся друг на друга.

Математическим исследованием формы цветов и листьев занимался также Хабеннихт – геометр 19 столетия. Им был получен целый ряд уравнений, которые с весьма хорошим приближением выражали аналитически формы листьев клена, щавеля, ивы и т. д. Вот некоторые из этих кривых:

В полярных координатах можно описать при помощи косинусов кратных дуг линии, которые обрисовывают контуры листьев некоторых растений:

• кувшинки: (рис. а);
• кислицы: (рис. б);
• настурции: (рис. в);

• стрелолиста: (рис. г).

Рис. А Рис. Б Рис. В Рис. Г

1.4. Построение кусочно-заданной функции на примере построения эскиза национального орнамента

Свои исследования я продолжил, возник вопрос в построении графиков функций состоящих из нескольких кривых на заданном интервале. В качестве примера мною рассмотрено построение эскиза калмыцкого орнамента (геометрического) в Excel.

Если рассмотреть любой геометрический орнамент, то с математической точки он представляет собой набор прямых или кривых на заданном интервале, иногда на одном интервале может быть задано несколько различных линий. Совокупность этих линий и кривых образует рисунок который и будем считать орнаментом.

Также можно заметить, что орнамент представляет собой периодическую функцию (рисунок повторяется, через заданный интервал). Для того, чтобы построить заданный орнамент мы его построим на определенном интервале, а затем перенесем все вычисления на заданный шаг и т. д.

Приведенный ниже орнамент представляет собой семейство прямых заданных на отрезках, причем прямые параллельны одной из осей координат т.е. их уравнения принимают вид у =a или х =а.

Построим эти прямые.

Примеры таблиц вычислений:

(Полные вычисления можно увидеть в файле приложении1)

График функции приведен ниже:

Проделав данную исследовательскую работу я пришел к следующим выводам: Microsoft Excel предоставляет большие возможности для построения и исследования графиков функций.

Использование компьютерных программ для построения графиков функций, изучение их свойств и закономерностей, дает возможность рассмотреть большое количество примеров с минимальными усилиями. Данная работа предназначена в помощь учителям при изучении функции, а также ученикам с целью заинтересовать их математикой, информатикой, показав возможности использования информационных технологий на уроках математики.

В классе котором я обучаюсь, мною была дана обзорная лекция с практическим ознакомлением, на которой одноклассников я ознакомил учащихся с принципами построения графиков функций на примере тригонометрических функций, был предложен вариант построения графика функции с параметром. Построение графиков с параметром позволяет рассмотреть особенности графика в зависимости от параметра, изучить свойства функции, научиться строить графики функций путем преобразований исходной. В какой то мере благодаря этой работе мои одноклассники разобрались на отлично с темой построение графиков тригонометрических функций и их преобразований.

Мне удалось добиться поставленных целей работы. Был проработан алгоритм построения графиков элементарных функций, для построения кривых высших порядков мною был изучен дополнительный материал: построение кривых высших порядков в полярных координатах, где основополагающим является угол преобразования и радиус вектор. Был проработан алгоритм решения данной задачи: при помощи формул перехода от полярных координат к декартовым и обратно.

Изучая кривые линии высших порядков, ведь используя Microsoft excel, это не составляет труда, мне представился удивительный мир графиков различных функций. Оказывается таким образом можно построить, меняя параметры в данных уравнениях графики, которые напоминают листья растений и деревьев (например: кувшинки или лотоса). Оказывается математика — живая наука.

Опыт, приобретенный мною в процессе выполнения работы, несомненно, пригодится мне в дальнейшей жизни. Так, например, умея строить графики уравнений с параметрами можно найти корни уравнений и их зависимость от введенного параметра, что даст наглядную картину решения данного уравнения. Это позволяет решать задания ЕГЭ по математике части С5.

Также данные навыки будут необходимы при построении графиков и диаграмм в дальнейшей профессиональной деятельности, так excel прикладная программа применимая во многих сферах деятельности человека, например бухгалтерии, дизайн, аналитика, инженерия и другие.

Строя график функции на примере орнамента у меня возник вопрос, который остался не разрешенным. Как вы видели, я строил график по интервалам, что конечно занимает некоторое время. Возникает вопрос, как упростить данные построения. У меня есть три способа решения данной проблемы: 1) попытаться найти оптимальное уравнение функции, которое позволить заменить одновременно несколько этапов построения. Для решения этого вопроса нужно провести поиск в математических источниках.

2) найти возможности программы Excel для решения этой задачи. Как я говорил, в данной программе, много возможностей, многие из них, я еще не изучил.

3) найти другие программы построения графиков, которые позволят построить график данных функций. Такие программы существуют, например Adgrapher или DPlot и др. Данные программы, я планирую изучить в дальнейшем. Оптимальным решением, конечно же, будет создание своей программы, используя языки программирования.

Источник: nsportal.ru

Общая схема исследования функции и построения графика

Для полного исследования функции и построения её графика рекомендуется использовать следующую схему:

1) найти область определения функции;

2) найти точки разрыва функции и вертикальные асимптоты (если они существуют);

3) исследовать поведение функции в бесконечности, найти горизонтальные и наклонные асимптоты;

4) исследовать функцию на чётность (нечётность) и на периодичность (для тригонометрических функций);

5) найти экстремумы и интервалы монотонности функции;

6) определить интервалы выпуклости и точки перегиба;

7) найти точки пересечения с осями координат, если возможно и некоторые дополнительные точки, уточняющие график.

Исследование функции проводится одновременно с построением её графика.

Пример 9 Исследовать функцию и построить график.

1. Область определения : ;

2. Функция терпит разрывв точках,;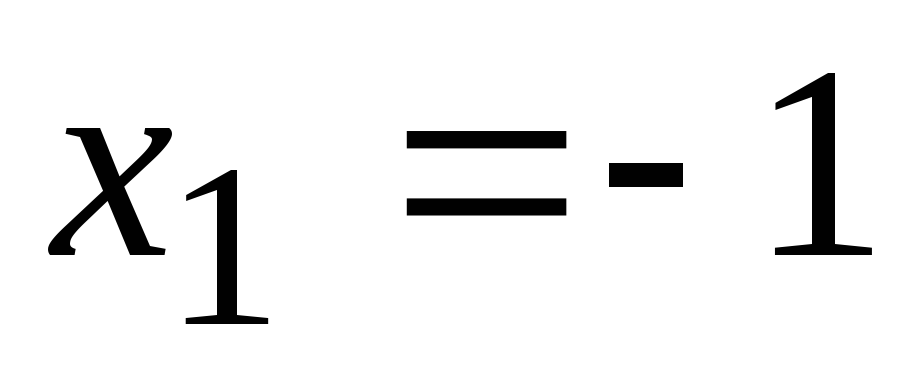

Исследуем функцию на наличие вертикальных асимптот.

;, ─ вертикальная асимптота.

;, ─ вертикальная асимптота.

3. Исследуем функцию на наличие наклонных и горизонтальных асимптот.

Прямая ─ наклонная асимптота, если, .

,.

Прямая ─ горизонтальная асимптота.

4. Функция является четной т.к. . Чётность функции указывает на симметричность графика относительно оси ординат.

5. Найдём интервалы монотонности и экстремумы функции.

.

Найдём критические точки, т.е. точки в которых производная равна 0 или не существует: ;. Имеем три точки;. Эти точки разбивают всю действительную ось на четыре промежутка. Определим знакина каждом из них.

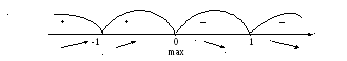
На интервалах (-∞; -1) и (-1; 0) функция возрастает, на интервалах (0; 1) и (1 ; +∞) ─ убывает. При переходе через точку производная меняет знак с плюса на минус, следовательно, в этой точке функция имеет максимум .

6. Найдём интервалы выпуклости , точки перегиба.

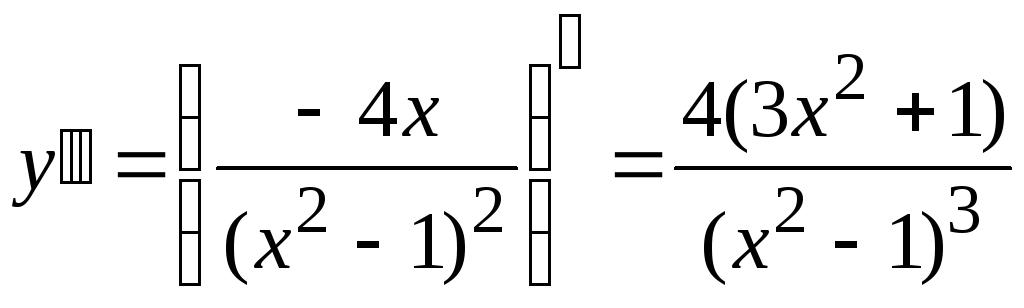
Найдём точки, в которых равна 0, или не существует.

не имеет действительных корней. , ,

Точки и разбивают действительную ось на три интервала. Определим знак на каждом промежутке.

Таким образом, кривая на интервалах ивыпуклая вниз, на интервале (-1;1) выпуклая вверх; точек перегиба нет, т. к. функция в точках и не определена.

7. Найдем точки пересечения с осями.

С осью график функции пересекается в точке (0; -1), а с осьюграфик не пересекается, т.к. числитель данной функции не имеет действительных корней.

График заданной функции изображён на рисунке 1.

Рисунок 1 ─ График функции

Применение понятия производной в экономике. Эластичность функции

Для исследования экономических процессов и решения других прикладных задач часто используется понятие эластичности функции.

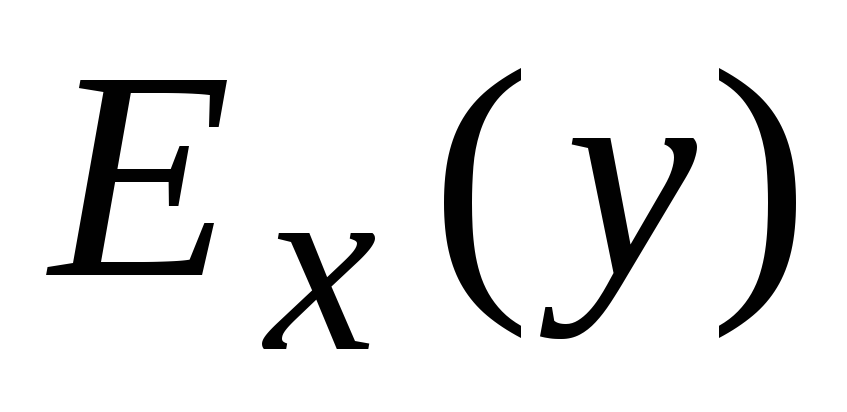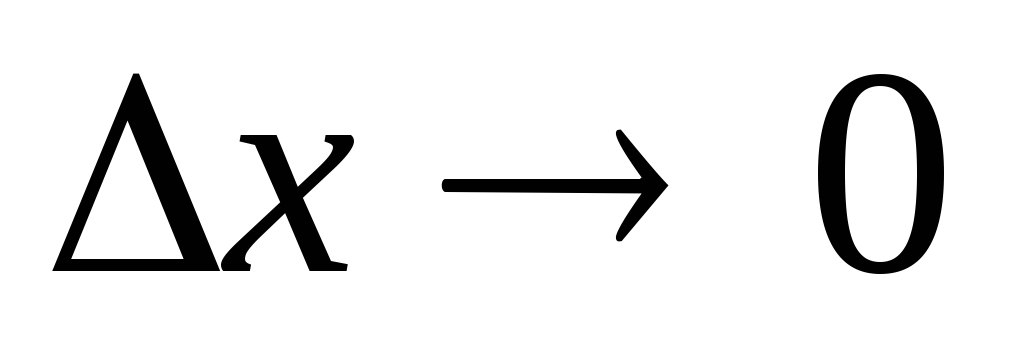Определение. Эластичностью функции называется предел отношения относительного приращения функциик относительному приращению переменнойпри, . (VII)

Эластичность функции показывает приближённо, на сколько процентов изменится функция при изменении независимой переменнойна 1%.

Эластичность функции применяется при анализе спроса и потребления. Если эластичность спроса (по абсолютной величине) 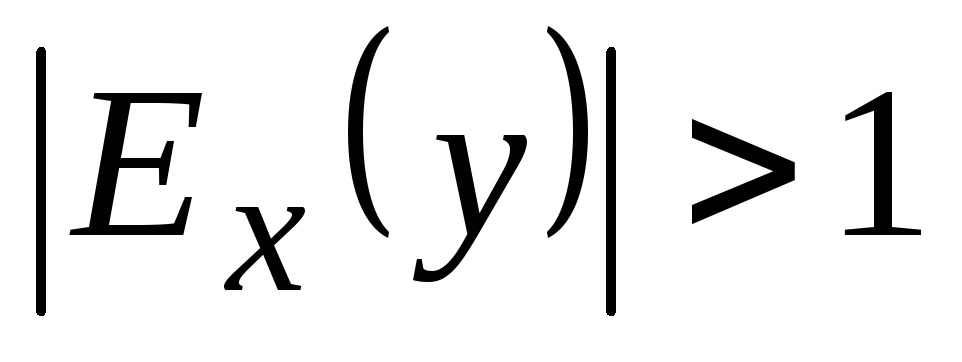, то спрос считают эластичным, если ─ нейтральным, если ─ неэластичным относительно цены (или дохода).

Пример 10 Рассчитать эластичность функции 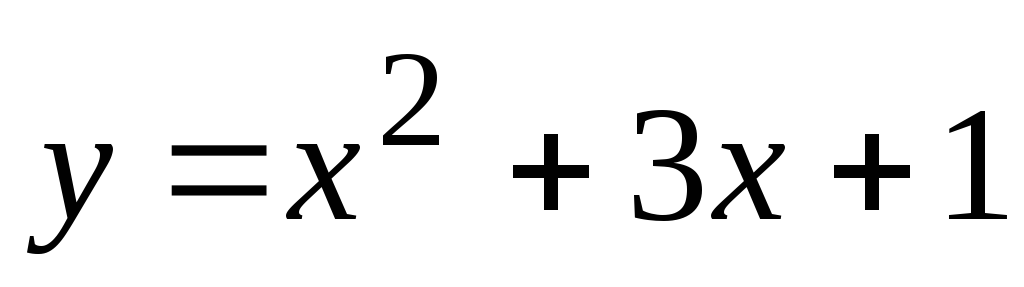и найти значение показателя эластичности для = 3.

Решение: по формуле (VII) эластичность функции:

.

Пусть х=3, тогда .Это означает, что если независимая переменная возрастёт на 1%, то значение зависимой переменной увеличится на 1,42 %.

Пример 11 Пусть функция спроса относительно ценыимеет вид, где─ постоянный коэффициент. Найти значение показателя эластичности функции спроса при цене х = 3 ден. ед.

Решение: рассчитаем эластичность функции спроса по формуле (VII)

.

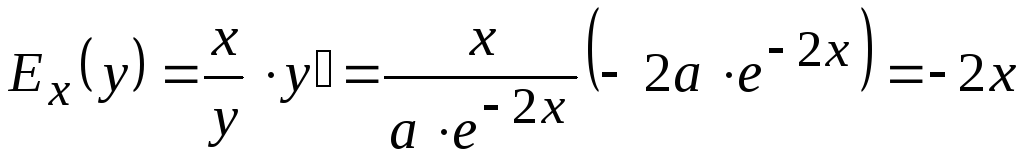
Полагая ден.ед., получим. Это означает, что при цене ден.ед. повышение цены на 1% вызовет снижение спроса на 6%, т.е. спрос эластичен.

Источник: studfile.net

Программа для исследование функции и построение ее графика

Задача 7. Провести полное исследование функции и построить её график. Исследование функции проводится в соответствии с планом полного исследования функции. Посмотрите образец такого исследования с построением графика. Введите номер своего варианта или решите задачу по образцу, приведённому ниже. Решение

7.3. Провести полное исследование функции и построить её график Решение. 1) Область определения: или , то есть . Таким образом: . 2) Точек пересечения с осью Ox нет. Действительно, уравнение не имеет решений. Точек пересечения с осью Oy нет, так как . 3) Функция ни чётная, ни нечётная.

Симметрии относительно оси ординат нет. Симметрии относительно начала координат тоже нет. Так как . Видим, что и . 4) Функция непрерывна в области определения ; .
Следовательно, точка является точкой разрыва второго рода (бесконечный разрыв). ; . Следовательно, точка является точкой разрыва второго рода (бесконечный разрыв). 5)Вертикальные асимптоты: Найдём наклонную асимптоту . Здесь ;

. Следовательно, имеем горизонтальную асимптоту: y=0. Наклонных асимптот нет. 6) Найдём первую производную. Первая производная: .
И вот почему . Найдём стационарные точки, где производная равна нулю, то есть . 7) Найдём вторую производную. Вторая производная: . И в этом легко убедится, так как . Найдём точки перегиба графика функции, в которых вторая производная обращается в ноль. То есть Тестовые интервалы: Результаты исследования функции занесем в таблицу.

Относительный максимум (-1;-2). 8) Данные таблицы нанесем на координатную плоскость. Используя результаты исследования функции, построим ее график функции.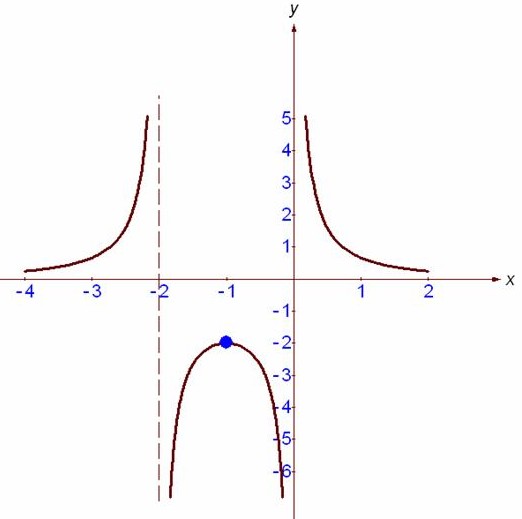

Решебники по математике:

Источник: kvadromir.com