В каждом доме есть свой порядок: сначала моем руки, затем едим обед, сначала все уроки — а потом гулять. Так вот, в математике тоже есть последовательность действий, которую важно соблюдать.
29 декабря 2020
· Обновлено 2 марта 2023
Основные операции в математике
Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).
Операции действия:
- сложение (+);
- вычитание (-);
- умножение (*);
- деление (:).
Операции отношения:
- равно (=);
- больше (>);
- меньше ( <);
- больше или равно (≥);
- меньше или равно (≤);
- не равно (≠).
Пройдите тест и узнайте, какие темы отделяют от пятёрки по математике
Привет! Это Макс, он хочет отпраздновать начало учебного года. Давай поможем Максу подготовиться к празднику
Жми на стрелки сверху, чтобы путешествовать в истории →
Простой пример, в котором главное не запутаться. Порядок действий в выражениях
Макс делал домашку и потерял счёт времени. Он забыл, что Саша и Чак совсем скоро придут в гости →
Посчитай, сколько времени нужно Максу на все дела
Максу понадобится 13 12 14 15 минут, чтобы все успеть
Первое дело уже в работе! Для торта Максу в магазине нужно докупить продукты→
Максу надо докупить мармелад, сгущёнку и яйца
Cколько рублей надо заплатить Максу?
Ответ: 23 рубля 24 рубля 21 рубль 22 рубля
Макс купил муку, яйца, масло, сгущёнку и мармелад. Начинаем готовить торт! →
Рассчитай, сколько весят ингридиенты для торта
4 * 50 = 250 200 220 230 грамм весят 4 яйца
142 + 150 + 137 = 429 432 427 426 грамм весят 3 яблока
6 * 7 = 44 46 42 48 грамма весит полстакана сахара
32 : 4 = 6 4 8 10 столовых ложек муки в стакане
В домофон звонят Саша и Чак, а Макс забыл прибраться! У вас всего несколько минут
Макс уберёт книги перед тем, как пропылесосить, а посуду помоет после того, как пропылесосит. В каком порядке Макс сделает дела?
Супер! Благодаря тебе Макс сделал все дела.
Дальше узнаешь свои результаты →
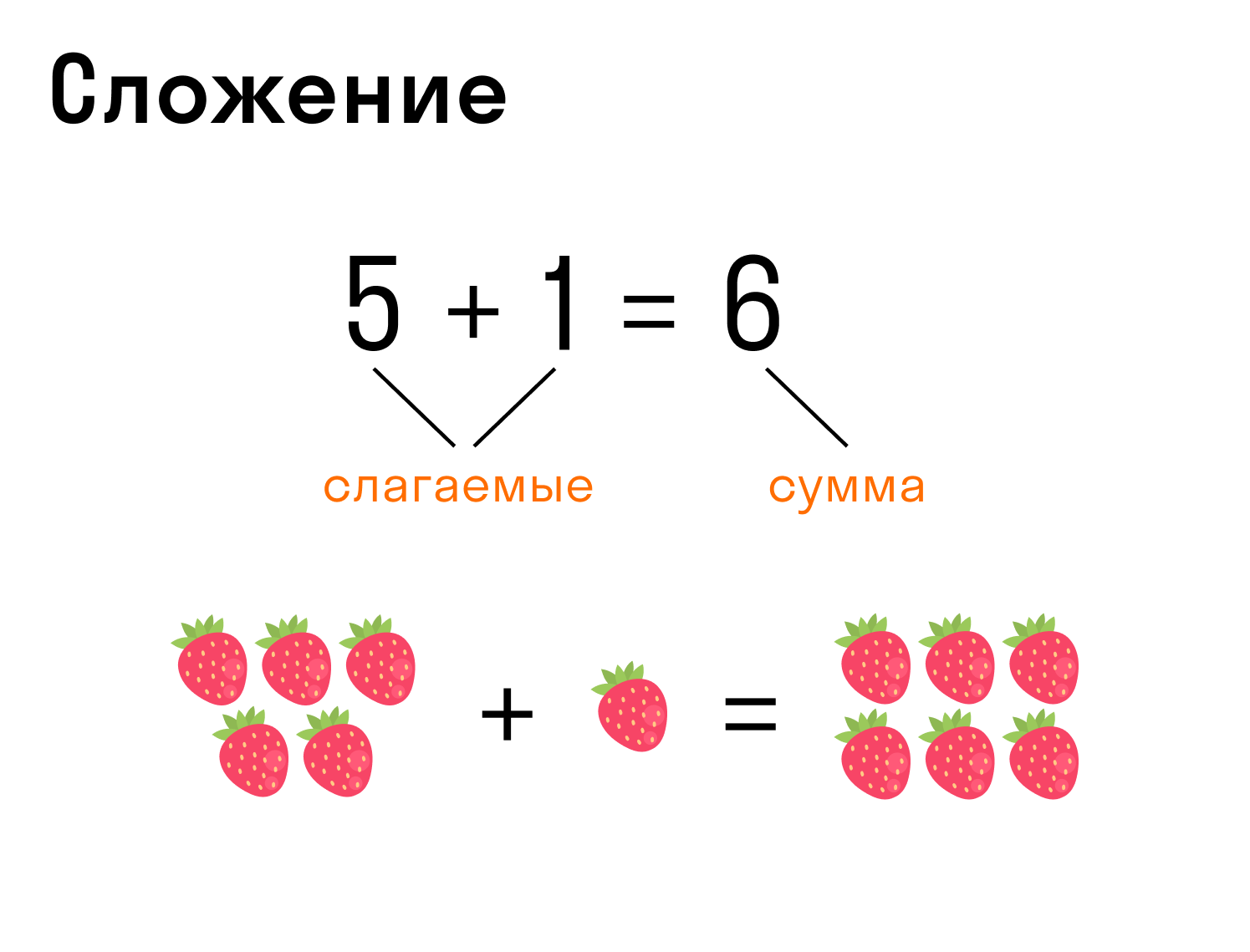
Сложение — операция, которая позволяет объединить два слагаемых.
- Запись сложения: 5 + 1 = 6, где 5 и 1 — слагаемые, 6 — сумма.
Вычитание — действие, обратное сложению.
- Запись вычитания: 10 — 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.
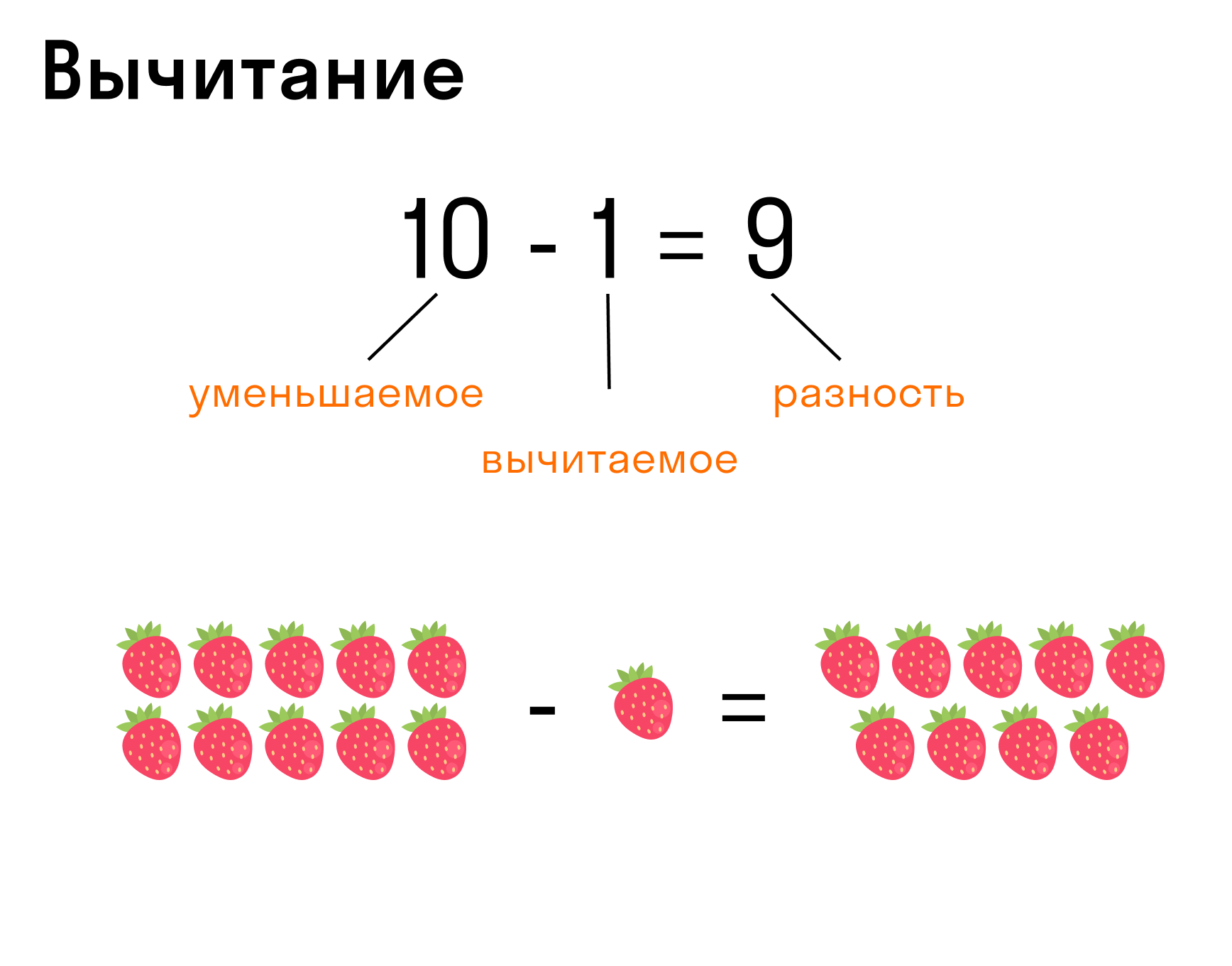
Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 — 1 = 9.
Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.
Арифметика и алгебра: порядок действий в вычислениях в математике
- Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.
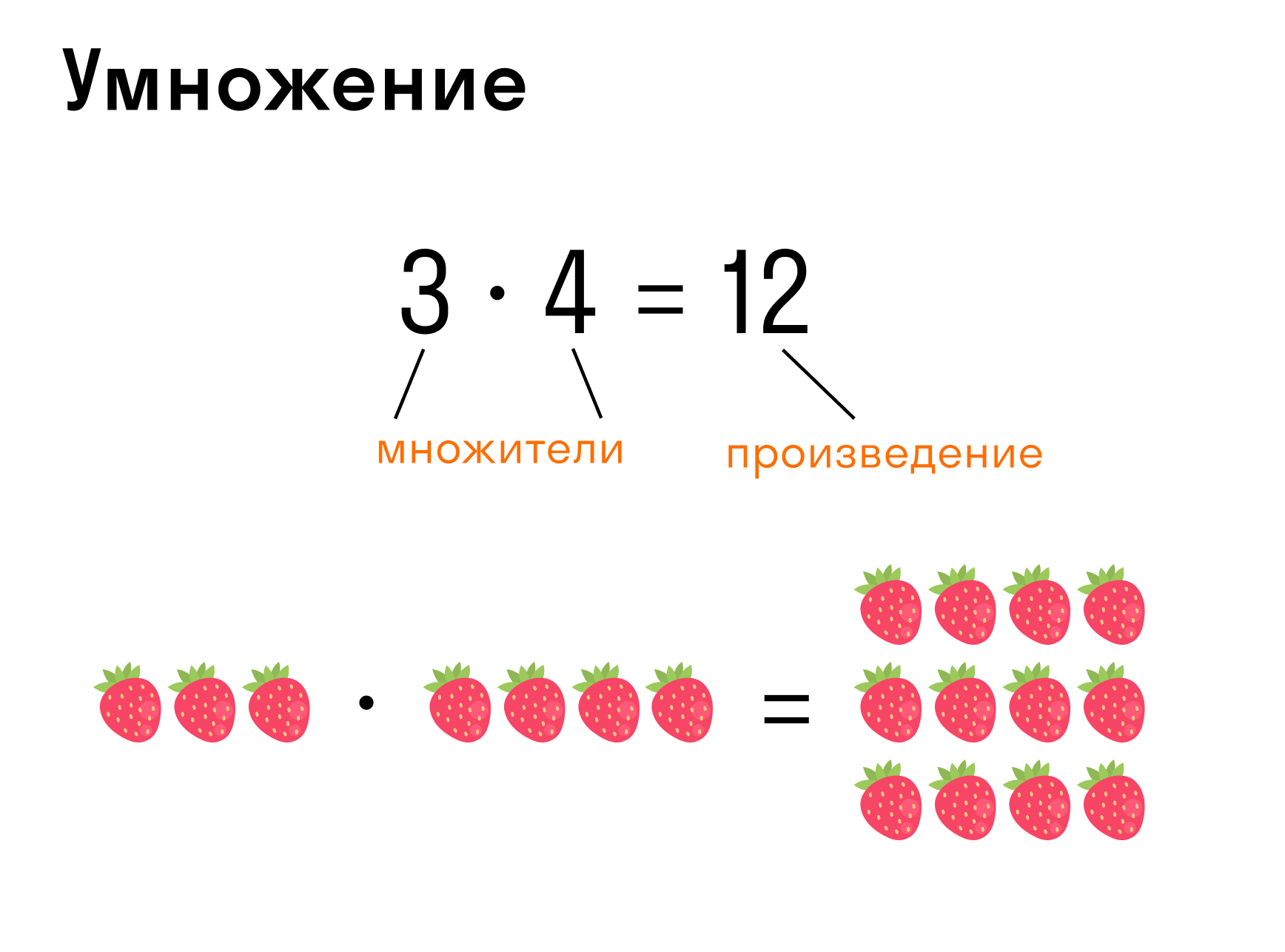
- 3 × 4 = 3 + 3 + 3 + 3, то есть число 3 сложили 4 раза само с собой.
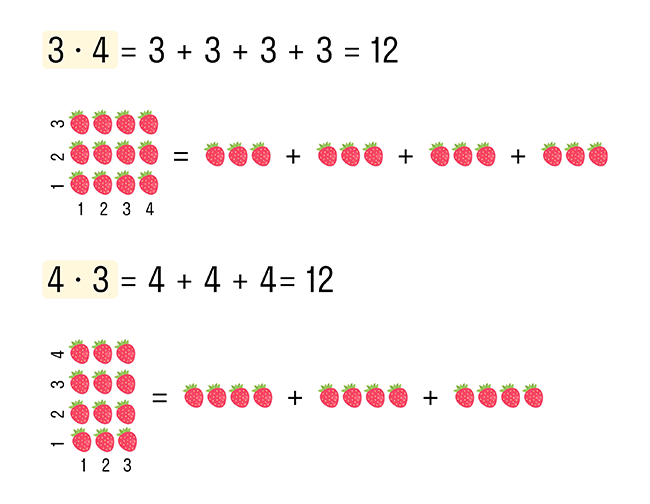
В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 × 2 = 5 + 5 = 10 и 2 × 5 = 2 + 2 + 2 + 2 + 2 = 10.
Поэтому и множитель, и множимое называют сомножителями.
Деление — арифметическое действие обратное умножению.
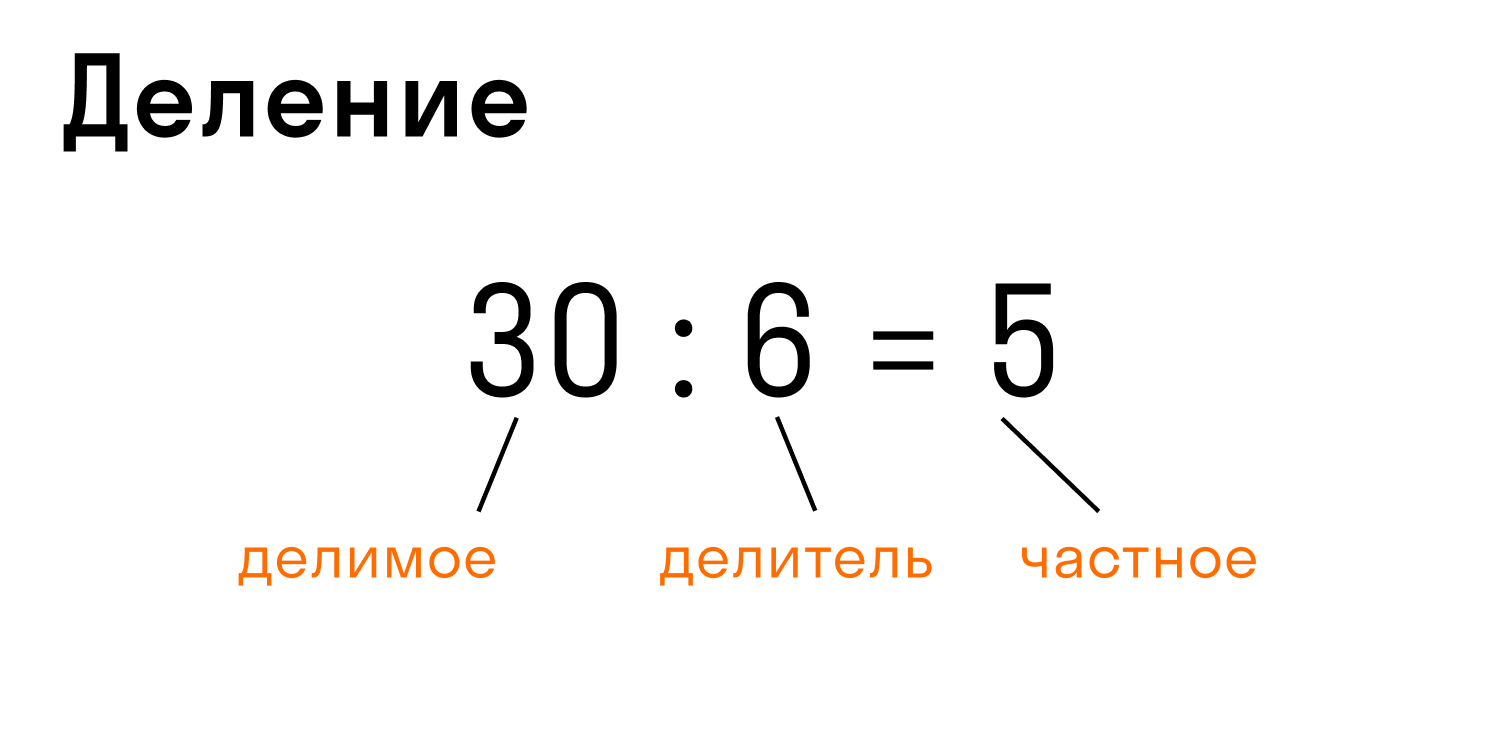
- Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.
В этом случае произведение делителя 6 и частного 5 в качестве проверки дает делимое 30.
Сложение и вычитание, умножение и деление попарно представляют обратные друг другу действия. А теперь давайте узнаем порядок выполнения арифметических действий.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Источник: skysmart.ru
Порядок действий в математике
Какое действие выполнить в первую очередь: сложение или умножение? Простые для внимательного школьника примеры вида 2 + 2 × 2 не всякий взрослый решит правильно. Разберемся вместе, как без ошибок решать числовые выражения со скобками и без.
Решайте математические и логические задачи и примеры на ЛогикЛайк!
Выберите возраст для старта
Более 5500 увлекательных заданий для развития математических способностей и логического мышления — в онлайн‑курсе ЛогикЛайк.
Для чего нужен порядок действий?
Большинство действий, которые мы выполняем в жизни имеют свой порядок. Согласитесь, чтобы пойти в магазин вы сначала одеваетесь, а затем выходите на улицу, а не наоборот. Так же и в математике, у арифметических действий есть своя очередность, которую необходимо соблюдать.
Вы уже решали простые примеры на сложение, вычитание, умножение или деление. Более сложные примеры называют числовыми выражениями, они содержат два, три и даже больше действий.
60 — 24 : 8 + 2 × 4
Чтобы правильно решить подобные примеры, нужно знать какое действие выполняется раньше других.
Кто придумал порядок действий?
В 1560 году французский логик и математик Пьер де ла Раме в своей книге «Алгебра» впервые применил определенный способ выполнения последовательности действий.
Порядок действий в примерах и картинках
Вам задали решить длинный пример – не паникуйте, это проще простого, если знать порядок действий.
Порядок действий – это определенная последовательность выполнения цепочки арифметических действий.
В каком порядке выполнять действия?
Первыми всегда выполняются действия в скобках с учетом приоритетности. Приоритет действий: умножение или деление выполняются раньше, чем сложение или вычитание. При равном приоритете действия выполняются слева направо.
- Скобки (если они есть)
- Умножение или деление
- Сложение или вычитание
Порядок действий в выражениях без скобок
Вычислим значение выражения, применяя порядок выполнения действий.
Порядок выполнения равнозначных действий
- Умножение и деление равнозначны. Если умножение стоит слева от деления, то умножение выполняется первым. Если деление находится слева от умножения, сначала выполняется деление.
- Сложение и вычитание равнозначны. Если сложение стоит слева от вычитания, то сложение выполняется первым. Если вычитание находится слева от сложения, сначала выполняется вычитание.
Равнозначные действия выполняются по очереди слева направо.
Пример: 12 + 6 — 8
В данном выражении нет скобок и знаки равнозначные по очередности (сложение, вычитание), значит выполнять их мы будем по очереди слева направо.
Получаем результат 10.
Пример: 6 + 4 × 8 — 7
В данном выражении нет скобок, значит сначала мы будем выполнять умножение.
Когда остается два равнозначных действия, мы будем их выполнять слева направо по порядку. В данном случае сначала выполним сложение, а затем вычитание.
Источник: logiclike.com
Порядок выполнения действий, правила, примеры
Когда мы работаем с различными математическими выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий: деление и умножение, сложение и вычитание степеней и др. Когда нужно сделать расчет и преобразование или вычитание значение, очень важно соблюдать правильную очередность или расстановку этих действий. Другими словами, действия в арифметике имеют свой особый порядок выполнения. Порядок действий в математике и для любого математика крайне важен.
В этой не слишком длинной и сложной статье мы расскажем, какие действия должны делаться математически в первую очередь, а какие после (к примеру, сначала идет деление или умножение). Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения или символы, а также знаки деления, умножения, вычитания и сложения (к примеру, пять плюс ноль равно пять). Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует решать эти примеры по действиям. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах по действиям, которые включают в себя знаки корней, степеней и других функций.
Порядок вычисления простых выражений
Решение примеров по действиям в выражениях со скобками
Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:
Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.
Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.
Пример или образец задачи 4
Условие: вычислите, сколько будет равно 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 .
Решение
В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7 − 2 · 3 . Здесь нам надо умножить 2 на 3 и вычесть результат из 7 :
7 − 2 · 3 = 7 − 6 = 1
Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .
Теперь нам нужно подставить получившиеся значения в первоначальное выражение:
5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 5 + 1 · 2 : 2
Начнем с умножения и деления, потом выполним вычитание и получим:
5 + 1 · 2 : 2 = 5 + 2 : 2 = 5 + 1 = 6
На этом вычисления можно закончить.
Ответ: 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 6 .
Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такое задание.
Условие: вычислите, сколько будет 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) .
Решение
У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · ( 2 + 3 ) , а именно с 2 + 3 . Это будет 5 . Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5 . Мы помним, что сначала надо умножать, а потом слагать: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 . Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .
Ответ: 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) = 28 .
Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.
Допустим, нам надо найти, сколько будет ( 4 + ( 4 + ( 4 − 6 : 2 ) ) − 1 ) − 1 . Начинаем с выражения во внутренних скобках. Поскольку 4 − 6 : 2 = 4 − 3 = 1 , исходное выражение можно записать как ( 4 + ( 4 + 1 ) − 1 ) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению ( 4 + 5 − 1 ) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.
Разберем пример такого вычисления.
Условие: найдите, сколько будет ( 3 + 1 ) · 2 + 6 2 : 3 − 7 .
Решение
У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид ( 3 + 1 ) · 2 + 36 : 3 − 7 .
Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание (слагаемое и вычитаемое).
( 3 + 1 ) · 2 + 36 : 3 − 7 = 4 · 2 + 36 : 3 − 7 = 8 + 12 − 7 = 13
Ответ: ( 3 + 1 ) · 2 + 6 2 : 3 − 7 = 13 .
В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.
Источник: zaochnik-com.com