Когда дело доходит до решения длинных примеров по математике, легко запутаться в порядке действий. Это может привести к неправильным ответам, плохим отметкам, разочарованию и даже к ненависти к математике. Чтобы этого избежать, можно сделать несколько вещей, которые известны каждому, но я напомню:
- Начинаем решать пример слева направо.
- Следуйте порядку операций: сначала скобки, потом умножение или деление, сложение или вычитание. Это порядок, в котором мы должны выполнять операции при решении примеров. Начинаем решение с того блока, который дан в скобках и двигаемся дальше.
- Решаем пример шаг за шагом слева направо, для этого разбиваем его на более мелкие шаги и решаем каждый шаг по отдельности, то есть по действиям. Это может облегчить понимание и решение примера.
- Не торопитесь! Из-за спешки и невнимательности можно запутаться.
- Легко сделать ошибки, если все вычисления вы пытаетесь сделать в своей голове. Запишите каждое действие в тетради подробно или воспользуйтесь черновиком.
- Проверьте свою работу: убедитесь, что вы правильно выполнили порядок действий и что ответ записан. А то очень распространенная ошибка школьников — решили весь пример по действиям, а ответ после знака равно не записан.
Пересчитывать всё заново не обязательно, но аккуратность и последовательность работы следует проверить.
Простой пример, в котором главное не запутаться. Порядок действий в выражениях
Запоминаем порядок действий
Рисуем в тетрадке или на большом плакате на отдельном листе лесенку .
— Представь, что решение примера — это подъем по лестнице. Мы поднимаемся на первую ступеньку — там скобки, потом на вторую — там умножение и деление, на третью — там сложение и вычитание. То есть порядок действий при решении примеров запоминается такой: скобки, умножение и деление, сложение и вычитание. Решённый пример — это самый верх лестницы! Мы туда забрались!
Молодцы!
Такой плакат, составленный самостоятельно, позволит ребенку запомнить порядок действий и больше никогда не ошибаться и не путаться в них.
Не путаемся при решении длинных примеров
Бывает такое, что порядок действий, что за чем решается, ребенок понимает отлично, а ошибки в длинных примерах всё равно есть. И я сейчас не затрагиваю арифметические ошибки, а только систему решения примеров по действиям.
В школе учат решать так:
Расставляем наверху числа — это номера действий. Под примером решаем по действиям.
У ребенка могут возникнуть вопросы ещё на этапе расстановки порядка действий. Он знает, что первое действие — скобка. Над всей скобкой он ставит номер 1. Но внутри этой скобки есть два действия, которые он может не воспринять.
Далее от 470 результат вычисления «скобки» нужно будет просто отнять. Здесь нет сложностей, но что делать с результатом из скобки в этом примере?
Какое будет второе действие: 8 умножить на 4 или результат «скобки» разделить на 7? А может быть, нужно сначала от 40 отнять результат «скобки»? И пятое действие — самое сложное. Какой результат от чего отнимать: то, что получилось во втором действии или то, что получилось в четвертом действии минус то, что получилось в третьем действии? Короче, путаница полная.
Как решать примеры со скобками? Порядок действий в выражениях | Математика
Для того чтобы её не было, нам надо научиться видеть в примерах не отдельные числа, а блоки.
Дело в том, что взрослый человек видит пример вида 10 — 8 : 2 не как три отдельные числа, а как два. Блок 8 : 2 воспринимается мозгом как одно целое число. Так ему легче решать пример. И такое восприятие выражений приходит к человеку к старшим классам.
Когда ребенок ещё маленький, он воспринимает пока только числа как числа. Наша задача — научить воспринимать их группами, чтобы решать примеры без путаницы.
Для этого подойдёт математическая игра . Придумываем длинный пример на весь лист. Числа не важны, считать его мы не будем, а просто придумаем и запишем:
Далее берём фломастер (просто потому что дети очень любят работать с фломастерами) и обводим все скобочки в этом примере в кружочки. Именно их мы будем решать в первую очередь.
Далее фломастером другого цвета обводим все группы чисел со знаками умножения и деления. Объясняем ребенку, что мы обводим их как будто в единое число.
В некоторых случаях круги будут пересекаться.
После того как поработали таким образом с этим длинным примером, то заметили, что ребенок уже видит выражения с умножением и делением по-другому, он будет воспринимать их как единую группу.
Придумываем ещё несколько примеров на всю страницу, чтобы потренироваться таким образом. В течение нескольких дней регулярно играем в эту игру.
Результаты будут видны очень быстро, особенно с примерами на умножение и деление внутри одного большого примера.
Это упражнение воспринимается ребенком именно как игра, потому что в нем не нужно ничего считать, нет напряжения мозга, а есть только яркие, позитивные кружочки.
Попробуйте это упражнение, а потом дайте длинный пример для вычисления по действиям и для закрепления, где уже не нужно обводить круги, а нужно применить полученные знания и навыки.
Успехов вам в математике!
Источник: dzen.ru
интернет проект BeginnerSchool.ru
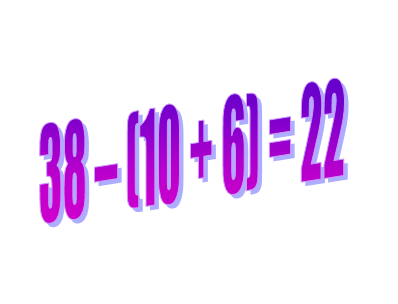
Сегодня мы поговорим о порядке выполнения математических действий. Какие действия выполнять первыми? Сложение и вычитание, или умножение и деление. Странно, но у наших детей возникают проблемы с решением, казалось бы, элементарных выражений.
Порядок выполнения действий:
Читаем выражение слева направо и выбираем порядок действий по приоритету. Сначала выполняем действия в скобках. Затем умножение и/или деление. Далее складываем и вычитаем.
Если скобки имеют несколько вложений, то есть если внутри скобок есть ещё скобки, то сначала выполняем действия во внутренних скобках. Для простоты понимания, выражение в скобках можно воспринимать как самостоятельное выражение, то есть как отдельный пример, который надо решить. Внутри скобок действия выполняются согласно тому же порядку: Действия в скобках, затем умножение/деление, затем сложение/вычитание.
Умножение и деление не имеет между собой приоритета и выполняются слева направо, также как и сложение с вычитанием.
38 – (10 + 6) = 22;
Итак, вспомним о том, что сначала вычисляются выражения в скобках
1) в скобках: 10 + 6 = 16 ;
2) вычитание: 38 – 16 = 22 .
Если в выражение без скобок входит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку слева направо.
10 ÷ 2 × 4 = 20;
Порядок выполнения действий:
1) слева направо, сначала деление: 10 ÷ 2 = 5 ;
2) умножение: 5 × 4 = 20 ;
10 + 4 – 3 = 11 , т.е.:
Если в выражении без скобок есть не только сложение и вычитание, но и умножение или деление, то действия выполняются по порядку слева направо, но преимущество имеет умножение и деление, их выполняют в первую очередь, а за ними и сложение с вычитанием.
18 ÷ 2 – 2 × 3 + 12 ÷ 3 = 7
Порядок выполнения действий:
4) 9 – 6 = 3 ; т.е. слева направо – результат первого действия минус результат второго;
5) 3 + 4 = 7 ; т.е. результат четвертого действия плюс результат третьего;
Если в выражении есть скобки, то сначала выполняются выражения в скобках, затем умножение и деление, а уж потом сложение с вычитанием.
30 + 6 × (13 – 9) = 54 , т.е.:
1) выражение в скобках: 13 – 9 = 4 ;
2) умножение: 6 × 4 = 24 ;
3) сложение: 30 + 24 = 54 ;
Итак, подведем итоги. Прежде чем приступить к вычислению, надо проанализировать выражение: есть ли в нем скобки и какие действия в нем имеются. После этого приступать к вычислениям в следующем порядке:
1) действия, заключенные в скобках;
2) умножение и деление;
3) сложение и вычитание.
- Основные содержательные линии в математике – вычислительные навыкиПродолжаем тему «основные содержательные линии курса математики начальной школы». В.
- Деление и другие математические действияМы уже говорили о делении и об основных правилах деления.
- Деление в столбикДеление многозначных или многоразрядных чисел удобно производить письменно в столбик.
- Математика – 3 классПродолжим изучение предметов, которые изучают наши дети в начальной школе.
- Основные содержательные линии в математике – найти значение выраженияПродолжаем рубрику «основные содержательные линии курса математики начальной школы». В.
Понравилась статья — поделитесь с друзьями:
Оставляйте пожалуйста комментарии в форме ниже
Отзывов (60)
Полезная статья. Спасибо!
Очень все понятно. Для детей важна такая разъяснительная работа. Где Вы были, когда я пошла в школу?
)) Покажу сыну, пусть изучает.
Я это вроде все помню. Спасибо )
Спасибо, сайт нужный. Честно говоря, уже кое – что подзабыла, а уроки с внучкой делаем. Вот, вспомнилось…
Очень необычная тематика сайта. Но тем, наверное, он и интересен. Иногда не знаешь, как объяснить ребенку тот или иной материал школьной программы.
Какое подспорье для родителей. И полезности для деток. Не всегда они материал усваивают в школе.
Сам учитель. Сайт очень полезный. Детям и родителям – хорошее подспорье
4217*4-(64385-39288)*3+321*1000=
Вы взяли пример из головы, в начальной школе не изучают отрицательных чисел, а также не оперируют такими большими числами. Результат пятого действия будет отрицательным.
Но попробуем решить данный пример:
1) Выражение в скобках: 64385 – 39288 = 25097
Далее умножение:
2) 4217 * 4 = 16868
3) 25097 * 3 = 75291
4) 321 * 1000 = 321000
Теперь слева на право
5) 16868 – 75291 = -58423 (. )
Это уже шестой класс, тема “Сложение положительных и отрицательных чисел”
6) -58423 + 321000
От перемены мест слагаемых сумма не меняется:
321000 + (-58423) = 321000 – 58423 = 262577
Помогите люди добрые.
Я тут читал кое где в иностранной литературе, что если в выражении есть действия двух уроовней 1(сложение и вычитание) и 2 (умножение и деление)
к примеру 20-6:3х2+2=
то в первую очередь должно выполнятся действия 2-ого уровня, потом 1-го. Но загвоздка с тем, что говорится – надо выполнить сперва умножение а потом деление, а не как нас учили по правилу слева направо.
Объясните плз.
Обязательно слева на право, так как умножение и деление равноценны. Но, если представить умножение в виде дроби: (6/3)*2 тогда 2 перенесется в числитель и первым выполняется умножение
(6 * 2)/3 = (6:3)*2 = 4.
То есть порядок выполнения важен!
Помогите решить пример у всех расходятся ответы
6/2*(1+2)
ответь пожалуйста
Если 6 : 2 * (1 + 2) =
1) 1 + 2 = 3
2) 6 : 2 = 3
3) 3 * 3 = 9 Если
6
———-
2 * (1 + 2)
то есть 6 : (2 * (1 + 2))
1) 1 + 2 = 3
2) 2 * 3 = 6
3) 6 : 6 = 1 Это два разных примера.
Если 6 * (1 + 2)
———–
2
1) 1 + 2 = 3
2) 6 * 3 = 18
3) 18 : 2 = 9
Это тот же первый вариант Если Вы правильно написали, то это первый вариант и ответ 9
Очень жаль, если вы этому детей учите.. Примеры 6:2*(1+2) и 6/2*(1+2) одинаковые… никогда не было такого, чтобы черта дроби и двоеточие означали разные действия или определяли порядок действий.
В данном случае необходимо также учесть правило раскрытия скобок:
6:2*(1+2) = 6:(2*1 + 2*2) = 6:(2+4) = 6:6 = 1 – единственный верный ответ.
6:2*(1+2) и 6/2*(1+2) это абсолютно эквивалентные записи (то есть одинаковые). Порядок действий следующий:
1) 1+2 = 3
2) 6:2 = 3
3) 3*3 = 9 Ваш вариант с раскрытием скобок будет верен, если запись выражения будет следующей:
6:(2*(1+2)) = 1; Ваше недоумение понятно, оно имеет глубокие исторические корни, в старых учебниках по алгебре можно встретить упоминание о именно такой последовательности действий, как предлагаете вы. Это связанно с неоднозначностью интерпретации записи. Но в наше время это разночтение устранено. Так что не надо забивать людям голову неверной информацией, а тем более забивать этими пережитками прошлого головы детей.
Простой пример. Ребенок на уроке информатики на языке Паскаль запишет y:=6:2*(1+2) и, поверьте мне, получит y=9. Не ломайте детскую психику.
В связи с порядком действий бывают забавные ситуации когда человеку в руки попадает калькулятор с обратной польской записью, а он и понятия не имеет об этом. И начинается “Святая Война за Истину”. Будьте проще, меньше пафоса, мы все люди и нам свойственно ошибаться. Добра Вам.
Источник: beginnerschool.ru
Порядок действий
Для правильного вычисления значений числовых выражений, в которых нужно произвести более одного действия, необходимо знать установленный порядок выполнения арифметических действий.
Порядок действий без скобок
Установленный порядок арифметических действий без скобок:
- Если выражение содержит только действия на сложение и вычитание, то они выполняются в порядке следования — слева направо:

- Если выражение содержит только действия на умножение и деление, то действия выполняются в порядке следования — слева направо:

- Если в выражении присутствуют и умножение с делением, и сложение с вычитанием, то сначала выполняются умножение и деление в порядке их следования (слева направо), а затем сложение и вычитание в порядке их следования (слева направо):

Порядок действий со скобками
Если выражение содержит скобки, то сначала выполняются все действия внутри скобок, а затем все действия, находящиеся за скобками.
В числовых выражениях со скобками порядок выполнения арифметических действий такой же, как и в выражениях без скобок.

Скобки применяются для обозначения действий, которые нужно произвести раньше остальных. Скобки не влияют на порядок остальных действий в выражении, остальные действия выполняются в указанном порядке.
Дробная черта
Дробная черта в выражении может быть заменена на знак деления, в этом случае, всё что было над и под дробной чертой надо взять в скобки. Например:
| 13 + 2 | = (13 + 2) : (10 — 7). |
| 10 — 7 |
Знак деления в выражении можно заменить дробной чертой только в том случае, если это не нарушает порядок действий. Например, выражение:
нельзя заменить на
| 20 | , |
| 4(2 + 3) |
потому что такая замена нарушит порядок действий в данном выражении.
| 20 : 4(2 + 3) ≠ | 20 | ; |
| 4(2 + 3) |
| 20 | = 20 : (4(2 + 3)). |
| 4(2 + 3) |
Дробная черта в выражении заменяет скобки и означает, что надо вычислить отдельно выражение, стоящее в числителе, и отдельно выражение, стоящее в знаменателе, и первый результат разделить на второй.
Источник: izamorfix.ru