Признак делимости на 3: примеры, доказательство
Приступим к рассмотрению темы «Признак делимости на 3 ». Начнем с формулировки признака, приведем доказательство теоремы. Затем рассмотрим основные подходы к установлению делимости на 3 чисел, значение которых задано некоторым выражением. В разделе приведен разбор решения основных типов задач, основанных на применении признака делимости на 3 .
Признак делимости на 3 , примеры
Формулируется признак делимости на 3 просто: целое число будет делиться на 3 без остатка, если сумма входящих в его состав цифр делится на 3 . Если суммарное значение всех цифр, которые входят в состав целого числа, на 3 не делится, то и само исходное число на 3 не делится. Получить сумму всех входящих в целое число цифр можно с помощью сложения натуральных чисел.
Теперь рассмотрим примеры применения признака делимости на 3 .
Делится ли на 3 число — 42 ?
Решение
Для того, чтобы ответить на этот вопрос, сложим все цифры, входящие в состав числа — 42 : 4 + 2 = 6 .
Делим программу на потоки №3. Swift.GCD Синхронизация
Ответ: согласно признаку делимости, раз сумма цифр, входящих с восстав исходного числа, делится на три, то и само исходное число делится на 3 .
Для того, чтобы ответить на вопрос о том, делится ли на 3 число 0 , нам понадобится свойство делимости, согласно которому нуль делится на любое целое число. Получается, что нуль делится на три.
Существуют задачи, для решения которых прибегать в признаку делимости на 3 необходимо несколько раз.
Покажите, что число 907 444 812 делится на 3 .
Решение
Найдем сумму всех цифр, которые образуют запись исходного числа: 9 + 0 + 7 + 4 + 4 + 4 + 8 + 1 + 2 = 39 . Теперь нам нужно определить, делится ли на 3 число 39 . Еще раз складываем цифры, входящие в состав этого числа: 3 + 9 = 12 . Нам осталось провести сложение цифр еще раз для того, чтобы получить окончательный ответ: 1 + 2 = 3 . Число 3 делится на 3
Ответ: исходное число 907 444 812 также делится на 3 .
Делится ли на 3 число − 543 205 ?
Решение
Посчитаем сумму цифр, входящих в состав исходного числа: 5 + 4 + 3 + 2 + 0 + 5 = 19 . Теперь посчитаем сумму цифр полученного числа: 1 + 9 = 10 . Для того, чтобы получить окончательный ответ, найдем результат еще одного сложения: 1 + 0 = 1 .
Ответ: единица на 3 не делится, значит и исходное число на 3 не делится.
Для того, чтобы определить, делится ли данное число на 3 без остатка, мы можем провести деление данного числа на 3 . Если разделить число − 543 205 из рассмотренного выше примера столбиком на три, то в ответе мы не получим целого числа. Это точно также значит, что − 543 205 на 3 без остатка не делится.
Доказательство признака делимости на 3
Здесь нам понадобятся следующие навыки: разложение числа по разрядам и правило умножения на 10 , 100 и т.д. Для того, чтобы провести доказательство, нам необходимо получить представление числа a вида a = a n · 10 n + a n — 1 · 10 n — 1 + … + a 2 · 10 2 + a 1 · 10 + a 0 , где a n , a n − 1 , … , a 0 – это цифры, которые располагаются слева направо в записи числа.
Учимся считать — Учим сложение вычитание и умножение с Ежиком Жекой.
Приведем пример с использованием конкретного числа: 528 = 500 + 20 + 8 = 5 · 100 + 2 · 10 + 8 .
Запишем ряд равенств: 10 = 9 + 1 = 3 · 3 + 1 , 100 = 99 + 1 = 33 · 3 + 1 , 1 000 = 999 + 1 = 333 · 3 + 1 и проч.
А теперь подставим эти равенства вместо 10 , 100 и 1000 в равенства, приведенные ранее a = a n · 10 n + a n — 1 · 10 n — 1 + … + a 2 · 10 2 + a 1 · 10 + a 0 .
Так мы пришли к равенству:
a = a n · 10 n + … + a 2 · 100 + a 1 · 10 + a 0 = = a n · 33 . . . . 3 · 3 + 1 + … + a 2 · 33 · 3 + 1 + a 1 · 3 · 3 + 1 + a 0
А теперь применим свойства сложения и свойства умножения натуральных чисел для того, чтобы переписать полученное равенство следующим образом:
a = a n · 33 . . . 3 · 3 + 1 + . . . + + a 2 · 33 · 3 + 1 + a 1 · 3 · 3 + 1 + a 0 = = 3 · 33 . . . 3 · a n + a n + . . . + + 3 · 33 · a 2 + a 2 + 3 · 3 · a 1 + a 1 + a 0 = = 3 · 33 . . . 3 · a n + . . . + + 3 · 33 · a 2 + 3 · 3 · a 1 + + a n + . . . + a 2 + a 1 + a 0 = = 3 · 33 . . . 3 · a n + … + 33 · a 2 + 3 · a 1 + + a n + . . . + a 2 + a 1 + a 0
Выражение a n + . . . + a 2 + a 1 + a 0 — это сумма цифр исходного числа a . Введем для нее новое краткое обозначение А . Получаем: A = a n + . . . + a 2 + a 1 + a 0 .
В этом случае представление числа a = 3 · 33 . . . 3 · a n + . . . + 33 · a 2 + 3 · a 1 + A принимает такой вид, который нам будет удобно использовать для доказательства признака делимости на 3 .
Теперь вспомним следующие свойства делимости:
- необходимым и достаточным условием для того, чтобы целое число a делилось на целое число
b , является условие, по которому модуль числа a делится на модуль числа b ; - если в равенстве a = s + t все члены, кроме какого-то одного, делятся на некоторое целое число b , то и этот один член делится на b .
Мы заложили основу для того, чтобы провести доказательство признака делимости на 3 . Теперь же сформулируем этот признак в виде теоремы и докажем ее.
Для того, чтобы утверждать, что целое число a делится на 3 , нам необходимо и достаточно, чтобы сумма цифр, которая образует запись числа a , делилась на 3 .
Доказательство 1
Если взять значение a = 0 , то теорема очевидна.
Если ы возьмем число a , отличное от нуля, то модуль числа a будет натуральным числом. Это позволяет нам записать следующее равенство:
a = 3 · 33 . . . 3 · a n + . . . + 33 · a 2 + 3 · a 1 + A , где A = a n + . . . + a 2 + a 1 + a 0 — сумма цифр числа a .
Так как сумма и произведение целых чисел есть целое число, то
33 . . . 3 · a n + . . . + 33 · a 2 + 3 · a 1 — целое число, тогда по определению делимости произведение 3 · 33 . . . 3 · a n + . . . + 33 · a 2 + 3 · a 1 делится на 3 при любых a 0 , a 1 , … , a n .
Если сумма цифр числа a делится на 3 , то есть, A делится на 3 , то в силу свойства делимости, указанного перед теоремой, a делится на 3 , следовательно, a делится на 3 . Так доказана достаточность.
Если a делится на 3 , то и a делится на 3 , тогда в силу того же свойства делимости число
A делится на 3 , то есть, сумма цифр числа a делится на 3 . Так доказана необходимость.
Другие случаи делимости на 3
Целые числа могут быть заданы как значение некоторого выражения, которое содержит переменную, при определенном значении этой переменной. Так, при некотором натуральном n значение выражения 4 n + 3 n — 1 является натуральным числом. В этом случае непосредственное деление на 3 не может дать нам ответ на вопрос, делится ли число на 3 . Применение признака делимости на 3 также может быть затруднено. Рассмотрим примеры таких задач и разберем методы их решения.
Для решения таких задач может быть применено несколько подходов. Суть одного из них заключается в следующем:
- представляем исходное выражение как произведение нескольких множителей;
- выясняем, может ли хотя бы один из множителей делиться на 3 ;
- на основе свойства делимости делаем вывод о том, что все произведение делится на 3 .
В ходе решения часто приходится прибегать к использованию формулы бинома Ньютона.
Делится ли значение выражения 4 n + 3 n — 1 на 3 при любом натуральном n ?
Решение
Запишем равенство 4 n + 3 n — 4 = ( 3 + 1 ) n + 3 n — 4 . Применим формулу бинома Ньютона бинома Ньютона:
4 n + 3 n — 4 = ( 3 + 1 ) n + 3 n — 4 = = ( C n 0 · 3 n + C n 1 · 3 n — 1 · 1 + . . . + + C n n — 2 · 3 2 · 1 n — 2 + C n n — 1 · 3 · 1 n — 1 + C n n · 1 n ) + + 3 n — 4 = = 3 n + C n 1 · 3 n — 1 · 1 + . . . + C n n — 2 · 3 2 + n · 3 + 1 + + 3 n — 4 = = 3 n + C n 1 · 3 n — 1 · 1 + . . . + C n n — 2 · 3 2 + 6 n — 3
Теперь вынесем 3 за скобки: 3 · 3 n — 1 + C n 1 · 3 n — 2 + . . . + C n n — 2 · 3 + 2 n — 1 . Полученное произведение содержит множитель 3 , а значение выражения в скобках при натуральных n представляет собой натуральное число. Это позволяет нам утверждать, что полученное произведение и исходное выражение 4 n + 3 n — 1 делится на 3 .
Ответ: Да.
Также мы можем применить метод математической индукции.
Докажите с использованием метода математической индукции, что при любом натуральном
n значение выражения n · n 2 + 5 делится на 3 .
Решение
Найдем значение выражения n · n 2 + 5 при n = 1 : 1 · 1 2 + 5 = 6 . 6 делится на 3 .
Теперь предположим, что значение выражения n · n 2 + 5 при n = k делится на 3 . Фактически, нам придется работать с выражением k · k 2 + 5 , которое, как мы ожидаем, будет делиться на 3 .
Учитывая, что k · k 2 + 5 делится на 3 , покажем, что значение выражения n · n 2 + 5 при n = k + 1 делится на 3 , то есть, покажем, что k + 1 · k + 1 2 + 5 делится на 3 .
k + 1 · k + 1 2 + 5 = = ( k + 1 ) · ( k 2 + 2 k + 6 ) = = k · ( k 2 + 2 k + 6 ) + k 2 + 2 k + 6 = = k · ( k 2 + 5 + 2 k + 1 ) + k 2 + 2 k + 6 = = k · ( k 2 + 5 ) + k · 2 k + 1 + k 2 + 2 k + 6 = = k · ( k 2 + 5 ) + 3 k 2 + 3 k + 6 = = k · ( k 2 + 5 ) + 3 · k 2 + k + 2
Выражение k · ( k 2 + 5 ) делится на 3 и выражение 3 · k 2 + k + 2 делится на 3 , поэтому их сумма делится на 3 .
Так мы доказали, что значение выражения n · ( n 2 + 5 ) делится на 3 при любом натуральном n .
Теперь разберем подход к доказательству делимости на 3 , которых основан на следующем алгоритме действий:
- показываем, что значение данного выражения с переменной n при n = 3 · m , n = 3 · m + 1 и n = 3 · m + 2 , где m – произвольное целое число, делится на 3 ;
- делаем вывод о том, что выражение будет делиться на 3 при любом целом n .
Для того, чтобы не отвлекать внимание от второстепенных деталей, применим данный алгоритм к решению предыдущего примера.
Покажите, что n · ( n 2 + 5 ) делится на 3 при любом натуральном n .
Решение
Предположим, что n = 3 · m . Тогда: n · n 2 + 5 = 3 m · 3 m 2 + 5 = 3 m · 9 m 2 + 5 . Произведение, которое мы получили, содержит множитель 3 , следовательно само произведение делится на 3 .
Предположим, что n = 3 · m + 1 . Тогда:
n · n 2 + 5 = 3 m · 3 m 2 + 5 = ( 3 m + 1 ) · 9 m 2 + 6 m + 6 = = 3 m + 1 · 3 · ( 2 m 2 + 2 m + 2 )
Произведение, которое мы получили, делится на 3 .
Предположим, что n = 3 · m + 2 . Тогда:
n · n 2 + 5 = 3 m + 1 · 3 m + 2 2 + 5 = 3 m + 2 · 9 m 2 + 12 m + 9 = = 3 m + 2 · 3 · 3 m 2 + 4 m + 3
Это произведение также делится на 3 .
Ответ: Так мы доказали, что выражение n · n 2 + 5 делится на 3 при любом натуральном n .
Делится ли на 3 значение выражения 10 3 n + 10 2 n + 1 при некотором натуральном n .
Решение
Предположим что n = 1 . Получаем:
10 3 n + 10 2 n + 1 = 10 3 + 10 2 + 1 = 1000 + 100 + 1 = 1104
Если посчитать сумму цифр полученного числа, то получим 3 . Это позволяет нам утверждать, что полученное число делится на 3 .
Предположим, что n = 2 . Получаем:
10 3 n + 10 2 n + 1 = 10 6 + 10 4 + 1 = 1000 000 + 10000 + 1 = 1010001
Если посчитать сумму цифр этого числа, то мы снова получаем три. Это позволяет нам утверждать, что полученное число делится на 3 .
Так мы можем сделать вывод, что при любом натуральном n мы будем получать числа, которые делятся на 3 . Это значит, что 10 3 n + 10 2 n + 1 при любом натуральном n делится на 3 .
Ответ: Да
Источник: zaochnik.com
7 лучших приложений для разделения счетов для отслеживания общих расходов

Приложения для разделения счетов могут быть вашими лучшими друзьями во время групповых поездок или международных поездок, где требуется конвертация валюты в режиме реального времени. Больше никакой ментальной математики о конвертации валюты!
Встреча со старыми друзьями спустя долгое время? Какое чистое блаженство вы испытываете, не так ли? Внезапно ваша веселая вечеринка получает счета за все напитки и продукты, которые вы все выпили.
Постепенно все веселье улетучивается, и разговор начинает смещаться в сторону счетов и платежей. Все начинают опустошать свои кошельки, чтобы оплатить счета.
Что более отвратительно, так это то, что некоторые начинают обсуждать, как справедливо разделить счет между всеми участниками, чтобы никто не чувствовал себя обманутым. Хотя это рационально, но может привести к неловким ситуациям; предположим, что кто-то не в состоянии оплатить свою долю счета! Достаточно неловкости, чтобы испортить атмосферу!
Итак, как уберечь себя от этих неуклюжих ситуаций, связанных с разделением счетов после памятного вечера?
Переключитесь на одно из тех приложений для разделения счетов, которое позволяет легко оплачивать платежи, ежемесячные расходы и другие счета с другими участниками. Эти приложения могут стать вашим спасением в нескольких ситуациях, а не в одной.
Они обеспечивают прозрачность расходов с вашим соседом по комнате, чтобы узнать, какую долю счетов за коммунальные услуги они должны оплатить.
Приложения для разделения счетов кажутся осуществимыми? Слушайте нас чаще! Ниже приведены некоторые из приложений для разделения счетов, которые вы можете попробовать, чтобы окончательно отказаться от традиционного способа разделения счетов, чтобы каждый был уверен, что заплатил только то, на что имел право, и с ним не обошлись несправедливо.
Раздельно
Splitwise — это полнофункциональное приложение для разделения счетов, которое позволяет разделить расходы с членами вашей семьи или соседями по комнате и дает подробный обзор людей, которые занимали и одалживали деньги, что упрощает управление этими сведениями.
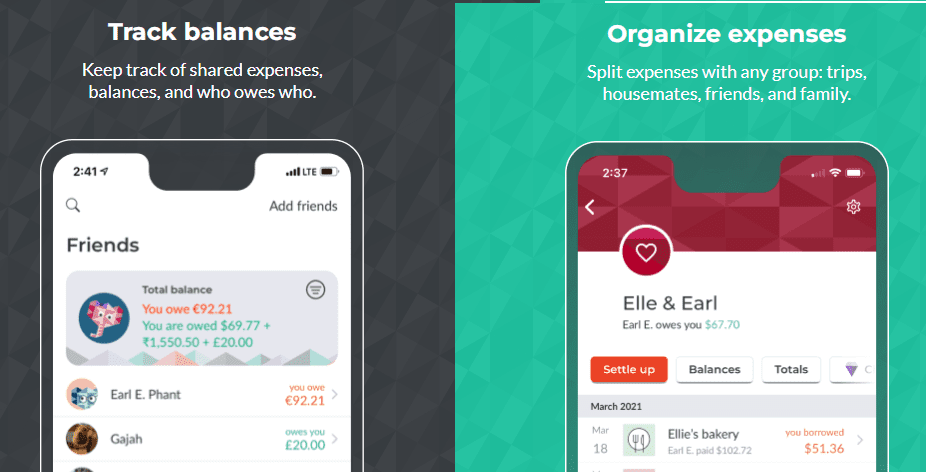
Приложение доступно в Интернете, на устройствах iOS и Android, и все участники могут легко присоединиться к группе, чтобы внести свой вклад в расходы.
Splitwise имеет очень простой интерфейс и предлагает богатый набор функций — вы можете классифицировать расходы, экспортировать отчеты в формате CSV, упростить долги и управлять повторяющимися расходами.
Существует также возможность разделить счета поровну или неравномерно между несколькими людьми, в зависимости от сценария. Splitwise поддерживает более семи языков и более 100 валют, что требует доказательства своей универсальности при разделении счета.
Приложение отправляет регулярные уведомления каждому члену группы, чтобы напомнить им о непогашенных остатках. Также можно совершать платежи через платформы PayPal и Venmo, а также наличными, которые необходимо записывать вручную.
Вкладка
Вкладка — лучший вариант, если вы хотите разделить счет за ужин между группой людей. Вы должны загрузить отсканированную копию квитанции, и все участники смогут получить доступ к счету в своем приложении. Затем пользователи могут нажать все, что они заказали, для оплаты, или несколько пользователей могут разделить стоимость одного заказа. Приложение автоматически рассчитывает налоги и чаевые и распределяет их пропорционально.
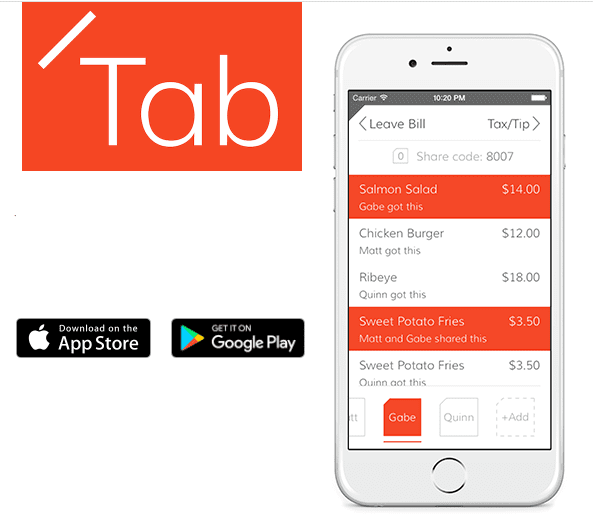
Приложение позволяет совершать цифровые платежи по счетам или просто платить наличными. Tab также поддерживает интеграцию с Venmo, поэтому вашу учетную запись Venmo также можно использовать для оплаты счета. Tab поддерживает облачную технологию для синхронизации всех действий в режиме реального времени и индивидуального подсчета суммы для каждого участника.
Tab, полезное обеденное приложение, доступно только для устройств Android и iOS. Более того, приложение доступно только в США из-за стандартного формата квитанций, налогов и родного языка.
Три счета
TriCount — это упрощенное приложение для смартфонов iPhone и Android, позволяющее управлять счетами путем явного распределения расходов между членами группы. Приложение пригодится в нескольких случаях — когда вы обедаете с друзьями или делите ежемесячные расходы с соседом по комнате. Пользователи должны создать группу и поделиться ссылками-приглашениями со своими друзьями.
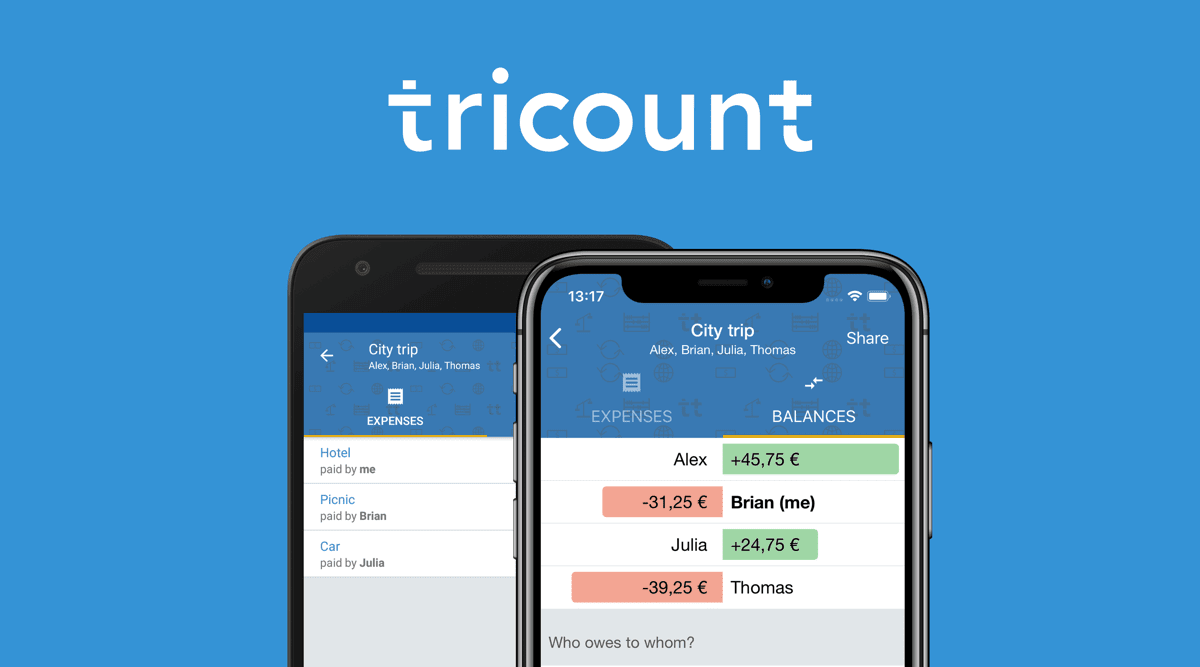
Как только все участники добавлены, они могут легко просмотреть свою долю расходов и оплатить себя. Вы найдете несколько методов разделения расходов, которые можно использовать, когда требуется неравномерное разделение.
Простой макет позволяет легко разделить расходы, а также приложение работает в автономном режиме. TriCount регулярно отправляет push-уведомления, чтобы держать всех в курсе предстоящих расходов, избавляя вас от стресса.
Опять же, регистрация в приложении необязательна, и приложение также работает в гостевом режиме. Некоторые базовые функции доступны бесплатно, а для доступа к расширенным функциям необходимо перейти на премиум-версию.
Венмо
Venmo — это одно из приложений, которое веками использовалось для оплаты счетов с соседом по комнате, оплаты обеда или оплаты ежемесячных расходов. Работа приложения проста; человек, которому должны деньги, может напрямую отправить деньги через Venmo. Точно так же другой человек может отправить платеж, чтобы потребовать, чтобы другой человек очистил ожидающие деньги.
Venmo предлагает несколько способов пополнения счета; оплата через дебетовую карту или банковский счет бесплатна. Оплату можно произвести из самого приложения или нажав на напоминание с помощью уникального кода.
Приложение Venmo доступно на устройствах Android и iOS для облегчения оплаты на ходу. Приложение намного изящнее, чем PayPal, и общее впечатление от него удовлетворительное. Venmo может быть легко интегрирован с другими приложениями, такими как SplitWise, и дает удобную возможность загружать изображения квитанций, чтобы упростить разделение счетов.
Акаса
Acasa — это не просто приложение для разделения счетов; он может предложить гораздо больше, чтобы сделать вашу жизнь проще. Он предназначен для настройки, управления, оплаты и разделения стоимости счетов с единой платформы. Бесплатное приложение выделяет ваши счета за домашнее хозяйство и пропорционально распределяет их между вами и вашим соседом по комнате.
Приложение Acasa доступно на устройствах Android и iOS; Вы можете загрузить его на свой смартфон и выбрать все счета за коммунальные услуги, которые вы хотите, чтобы Acasa обслуживала для вас: электроэнергия, широкополосный доступ, вода, телевидение и т. д.
Вы можете синхронизировать его со своим соседом по дому и проверить указанную цену в приложении. Также можно настроить автоматические ежемесячные платежи, и после включения Acasa разбивает счета на равные суммы и делает один платеж с банковского счета каждый месяц.
Управление ежемесячными расходами — это не только то, в чем Acasa хороша; Вы также можете использовать приложение, чтобы разделить счета, когда обедаете вне дома, наслаждаетесь вечерами пиццы, празднуете дни рождения и так далее.
Рассчитываться
SettleUp — отличный выбор для оплаты счетов и погашения долгов в простых и нестандартных ситуациях. Вы можете воспользоваться этим приложением, когда путешествуете за границу и вам приходится иметь дело с несколькими валютами. Как и TriCount, приложение также работает в автономном режиме и также предлагает бесплатную версию.
Курсы обмена валюты в режиме реального времени пригодятся, когда вам нужно разделить платеж в разных сценариях на международном уровне.
Разделение может быть сделано поровну или вы можете назначить определенную сумму для каждого человека в группе. Счета можно разделить напрямую по ссылке без регистрации в приложении.
SettleUp создает резервную копию всех разделений счетов, сделанных через приложение для Android и iOS, и синхронизирует их для участников группы. Бесплатная версия предлагает базовую функциональность, а премиум-версия усеяна функциями; вы можете загружать квитанции, управлять повторяющимися транзакциями, классифицировать расходы, разделять группы по цветовому коду и так далее.
Привязать и разделить
Наконец, у нас есть Snap Split доступно только для смартфонов Android и использует технологию OCR для сканирования квитанций и может читать квитанции OCR на 75 языках.
После сканирования квитанция также доступна в автономном режиме, и вы можете поделиться ею со своими друзьями, чтобы они могли оплатить расходы. Доступны несколько способов разделения счетов: получение квитанций или загрузка их из галереи, оплата по пунктам, внесение равных платежей, оплата пропорционально и многое другое.
Вы также найдете калькулятор чаевых, который принимает ввод и делит сумму чаевых между всеми участниками. Другие функции включают автоматическое определение налогов и скидок, совместное использование счетов и органайзер чеков.
Последние слова
Независимо от того, проводите ли вы ночь с друзьями или живете с соседом по комнате, сценарии, требующие от вас разделить счета, неизбежны. Интересно, что существует не одно, а множество приложений, которые упрощают запутанную задачу разделения счетов среди группы и гарантируют, что каждый хорошо знает, сколько им нужно внести, чтобы оплатить ожидающие счета.
Вы также можете изучить некоторые лучшие приложения для расчета чаевых для Android и iOS.
Источник: toadmin.ru
Написать функцию проверки делимости числа на 3
задача — Для делимости числа на 3 требуется, чтобы сумма цифр числа делились на 3. Написать функцию проверки делимости числа n, вводимого с клавиатуры, на 3.
__________________
Помощь в написании контрольных, курсовых и дипломных работ, диссертаций здесь
94731 / 64177 / 26122
Регистрация: 12.04.2006
Сообщений: 116,782
Ответы с готовыми решениями:
Написать функцию проверки делимости на 3 числа N, вводимого с клавиатуры
12.12. Для проверки делимости числа на 3, необходимо, чтобы сумма цифр числа делилась на 3.

Написать функцию для проверки символов
Написать функцию, которая возвращает значение True, если символ, полученный функцией в качестве.
Написать программу проверки умения складывать и вычитать числа в пределах 100.
Написать программу проверки умения складывать и вычитать числа в пределах 100. Программа должна.

Написать рекурсивную и нерекурсивную процедуры проверки наличия в списке заданного числа
Условие:Написать рекурсивную и нерекурсивную процедуры проверки наличия в списке заданного числа.
4341 / 1473 / 680
Регистрация: 12.03.2009
Сообщений: 5,310
1 2 3 4 5 6 7 8 9 10 11
function mod3(n:longint):boolean; var s:integer; begin s:=0; while n<>0 do begin s:=s+n mod 10; n:=n div 10; end; if s mod 3 = 0 then mod3:=true else mod3:=false; end;
Почетный модератор
64264 / 47564 / 32739
Регистрация: 18.05.2008
Сообщений: 115,182
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
uses crt; function Del3(n:longint):boolean; var s:byte; begin s:=0; while n>0 do begin s:=s+n mod 10; n:=n div 10; end; if s mod 3=0 then Del3:=true else Del3:=false; end; var k:longint; begin clrscr; write(‘Введите k=’); readln(k); if Del3(k) then write(‘число делится на 3’) else write(‘число не делится на 3’); readln end.
Источник: www.cyberforum.ru
2/3 часть. это сколько?
Вот вроде бы простой вопрос, но как часто люди теряются, встречая его в тексте. Например в кулинарных рецептах можно часто встретить- 2/3 или 1/3 стакана, или в строительстве 2/3 цемента.
Под этим подразумевается, что если мы берем вес, объем, размер, то делим на три равные части и затем из них забираем две части. Останется 1 часть.
То есть получается, что мы имеем 2/3 части от целого и остается 1/3 часть.
Из школьного курса — если у вас три яблока, то одно яблоко это 1/3 от общего количества, два яблока — это 2/3 от общего количества.
Если линейка 30 см, то 2/3 будет равно 20 см.
В математике в десятичном виде это будет равно 0,66666666(7).
система выбрала этот ответ лучшим
в избранное ссылка отблагодарить
Звездная пыль [17.5K]
Как интересно получилось с ответом, что невольно на память пришел момент из шоу Уральских пельменей:
Ведьма: -Это понимаешь ли, математика! А давайте ей голову отрежем чтобы не храпела!
Богатыри: -Хм.. если мы ей голову отрежем то, она ж умрет..
Колдунья: -А ты со своей анатомией в мою математику не лезь. — 7 лет назад
комментировать
Azama tik [55.2K]
6 лет назад
2/3 (две трети) — делим числители 2 на знаменатель 3 и получаем: 0,66666 (7).
Чему будет равно 2/3 года? — В году 12 месяцев. Делим 12 на 3 и получаем 4 месяца, которые мы умножаем на 2 и получаем 8 месяцев. Значит, 2/3 года равняется 8 месяцам;
А сколько будет 2/3 суток? — В сутках 24 часа. Совершаем те же самые действия и получаем результат 16 часов. Таким образом, 2/3 суток — это 16 часов;
2/3 минуты это сколько секунд? — В одной минуте 60 секунд. Делим на три равные части (20 секунд) и берем две таких равных частей (х2) и получаем 40 секунд. 2/3 минуты — это 40 секунд.
Это 2/3 круга:
Источник: www.bolshoyvopros.ru