Follow Us:
ADVERTISEMENT
Send Us Your Feedback / Suggestion
SEND FEEDBACK
For further assistance, please Contact Us
Обнаружен блокировщик рекламы
Ой! Похоже, вы используете Adblocker!
Поскольку мы изо всех сил пытались сделать для вас онлайн-расчеты, мы обращаемся к вам с просьбой предоставить нам разрешение, отключив Adblocker для этого домена.
Or
Disable your Adblocker and refresh your web page
ADVERTISEMENT
Имеется в наличии в приложении
Загрузите приложение Derivative Calculator для своего мобильного телефона, чтобы вы могли рассчитывать свои значения в своих руках.
калькулятор производных онлайн помогает найти производную функции онлайн по заданной переменной и показывает пошаговое дифференцирование. Для лучшего понимания вы можете взглянуть на приведенные примеры, чтобы различать функцию. Вы можете использовать этот калькулятор производной для упрощения первой, второй, третьей или до 5 производных.
Без сомнения, онлайн калькулятор производных – лучший способ получить производные в любой момент и даже поможет вам решить частные производные. Что ж, этот контекст предоставляет вам правила производной, как найти производную онлайн (шаг за шагом) и с онлайн калькулятор.
АЛГЕБРА С НУЛЯ — Что такое Производная?
Что такое производная?
В математике «производная» измеряет чувствительность к изменению выходного значения по отношению к изменению входного значения, но в расчетах производные являются центральными инструментами.
Пример:
В случае движущегося объекта по времени производной является изменение скорости за определенное время. Проще говоря, он измеряет, насколько быстро движущийся объект меняет свое положение с течением времени. Следовательно, производная – это «мгновенная скорость изменения» зависимой переменной по отношению к независимой переменной.
Процесс поиска производной известен как дифференциация. Следовательно, калькулятор производных будет большим подспорьем для быстрой идентификации производных.
Вы знали!
Многие статистики определяют производные просто по следующей формуле:
- (d / dx * f = f * (x) = limh → 0 f (x + h) – f (x) / h )
производная калькулятор функции f представлена как d / dx * f. «D» обозначает оператор производной, а x – переменную. Калькулятор деривативов позволяет вам находить деривативы без каких-либо затрат и ручных усилий. Однако производная от «производной функции» известна как вторая производная и может быть вычислена с помощью калькулятор производной второй производной. всякий раз, когда вам нужно обрабатывать до 5 деривативов вместе с последствиями правил дифференциации, просто попробуйте поискать деривативы, чтобы избежать риска ошибок.
Производные правила:
Есть определенные правила, по которым можно узнать производные. Эти полезные правила помогут вам вычислить деривативы. Следуя им, вы можете добавить вычитание и понять, как брать производную. Посмотрите ниже, чтобы узнать о них:
4. Вычисление производных примеры. Самое начало.
| Постоянный | c | |
| Линия | x | 1 |
| ax | a | |
| Квадрат | x 2 | 2x |
| Квадратный корень | √x | (½)x -½ |
| Экспоненциальный | e x | e x |
| a x | ln(a) a x | |
| Логарифмы | ln(x) | 1/x |
| loga(x) | 1 / (x ln(a)) | |
| Тригонометрия (x в радианах) | sin(x) | cos(x) |
| cos(x) | −sin(x) | |
| tan(x) | sec 2 (x) | |
| Обратная тригонометрия | sin -1 (x) | 1/√(1−x 2 ) |
| cos -1 (x) | −1/√(1−x 2 ) | |
| tan -1 (x) | 1/(1+x 2 ) |
| Умножение на константу | cf | cf’ |
| Правило власти | x n | nx n−1 |
| Правило суммы | f + g | f’ + g’ |
| Правило различия | f – g | f’ − g’ |
| Правило продукта | fg | f g’ + f’ g |
| Правило частного | f/g | (f’ g − g’ f )/g 2 |
| Взаимное правило | 1/f | −f’/f 2 |
| Правило цепи (как «Состав функций») |
f º g | (f’ º g) × g’ |
| Правило цепи (с помощью ‘ ) |
f(g(x)) | f’(g(x))g’(x) |
| Правило цепи (используя ( frac )) |
( frac = frac frac) | |
Как найти производную (решенные примеры)?
Здесь мы поможем вам решить производные задачи в соответствии с вышеупомянутыми правилами дифференциации. Итак, начнем!
Пример:
Какая производная от (cos (x) )?
Помимо ручных вычислений, вы можете посмотреть на приведенную выше таблицу, чтобы найти производную онлайн функции онлайн от (cos (x) )
Онлайн Вычислитель производных
Wolfram|Alpha отлично справляется с нахождением производных первого, второго или третьего порядка, значений производных в точке, а также с вычислением частных производных. Узнайте, что такое производные и как Wolfram|Alpha их находит.
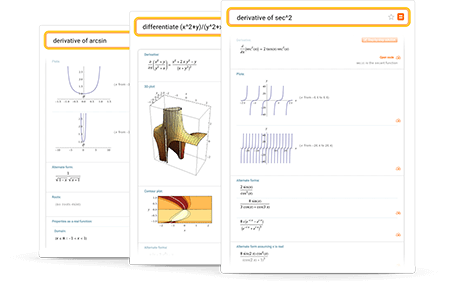
Рекомендации по составлению запросов
Вводите запросы на обычном английском языке. Использование скобок, в случае необходимости, позволяет избежать неоднозначностей в запросе. Вот некоторые примеры, иллюстрирующие запросы для вычисления производной.
Access instant learning tools
Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator
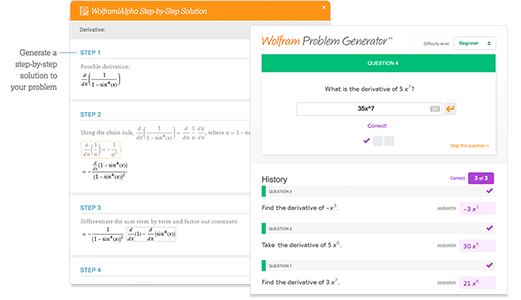
- Пошаговые решения »
- Wolfram Problem Generator »
Что такое производные?
Производная — это важный инструмент математического анализа, который отображает бесконечно малое изменение функции при изменении одной из её переменных.
Для функции , существует много способов обозначения производной относительно переменной . Наиболее распространенными являются обозначения и . Для обозначения кратной производной используют или . Кратные производные также называют производными старших порядков. Вторую производную также часто обозначают .
Производная в точке по определению равна . Этот предел не всегда определен, но когда он существует, о функции говорят, что она дифференцируема в точке . Говоря геометрически, дает тангенс угла наклона касательной к графику функции в точке .
Например, если , то и тогда мы можем найти вторую производную : . Производная является эффективным инструментом для решения многих прикладных задач. Например, она используется для определения локальных или глобальных экстремумов, точек перегиба, для решения задач оптимизации и описания траекторий движения объектов.
Каким образом Wolfram|Alpha находит производные
Wolfram|Alpha использует функцию D системы Mathematica, которая применяет таблицу тождеств, значительно превосходящую таблицы, приводимые в стандартных учебниках по математическому анализу. Она также использует ”хорошо известные” правила, такие как линейность производной, тождество Лейбница, правило дифференцирования степенной функции, правило дифференцирования сложной функции и т.п. Дополнительно, функция D использует ”менее известные” правила для вычисления производных широкого ряда специальных функций. Нахождение производных старших порядков использует некоторые правила, такие как общее тождество Лейбница, для увеличения быстродействия.
Источник: ru.wolframalpha.com
Калькулятор производных
Калькулятор производной поможет вам оценить производную онлайн. Калькулятор дифференцирования с шагами показывает промежуточные шаги, графики, корни, домен и т.д.
Калькулятор второй производной
Калькулятор частных производных
производная третьего порядка
Table of Contents
Get the Widget!
Introducing the Derivative Calculator. Add this tool to your site for easy and efficient derivative calculations.
Feedback
How easy was it to use our calculator? Did you face any problem, tell us!
Available on App
Download Weight loss Calculator App for Your Mobile.
Введение производного калькулятора с шагами
Исчисление — это раздел математики, который имеет дело с двумя основными понятиями: интегрированием и дифференцированием. Дифференцирование — это процесс нахождения скорости изменения функции по отношению к ее входной переменной. Это процесс, обратный интегрированию, то есть нахождению площади под кривой.
Расчет производных может быть техническим и требует надлежащего внимания и внимания. К счастью, калькулятор производных — это онлайн-инструмент, который предоставляет полное решение для дифференцирования. Калькулятор дифференциации с пошаговыми инструкциями помогает пользователям быстро и легко рассчитывать деривативы всего за несколько кликов.
онлайн калькулятор производных предоставляет полезные результаты в виде шагов, которые помогают пользователям и особенно учащимся подробно изучить эту концепцию. Пошаговые решения, предоставляемые калькулятором производных, также могут помочь пользователям понять правила и формулы, используемые при дифференцировании.
Помимо калькулятора дифференцирования, существуют и другие инструменты, такие как калькулятор второй производной, калькулятор третьей производной, калькулятор неявной дифференцировки и многие другие.
С помощьюпроизводный калькулятор и другие связанные инструменты и ресурсы, доступные на нашем веб-сайте, пользователи могут получить более глубокое представление об исчислении и о том, как оно используется в реальных приложениях. Итак, будь вы студентом, профессионалом или просто любителем математики, на нашем сайте есть, что вам предложить.
Чтобы максимально эффективно использовать наш веб-сайт и его инструменты, мы рекомендуем вам изучить все доступные ресурсы и узнать как можно больше об исчислении и дифференцировании.
Формулыиспользуется онлайн-калькулятором производных
Калькулятор производных обратных функций использует приведенную ниже формулу для нахождения производных функции. Формула производной:
Помимо стандартной формулы производной, существует множество других формул, с помощью которых можно найти производные функции. Эти расчетные формулы таковы:
$ frac(Sin x) = Cos x $ $ frac(Cos x) = -Sin x $ $ frac(tan x) = Sec ^2 x $ $ frac(Csx x) = -Csc x Cot x $ $ frac(Sec x) = Sec x Tan x $ $ frac< dx>(Cot x) = -Csc^2 x $
Производные правила, используемые калькулятором дифференцирования
С помощью производной мы можем найти наклон функции в любой заданной точке. Правила дифференцирования используются для вычисления производной функции. Наиболее важными правилами дифференциации являются:
$ frac[cf(x)] = c. fracf(x) $ Здесь c = действительное число
Как работает калькулятор производных?
Калькулятор производных — это онлайн-инструмент, который использует производные формулы и правила для вычисления точных результатов. Инструмент позволяет пользователям вводить данные в виде уравнения, которое можно вводить в различных форматах, включая стандартную алгебраическую запись, запись функции или даже графическое представление.
После ввода уравнения калькулятор производных применяет различные правила или формулы производных для его решения и вычисления производной. Эти правила и формулы могут включать правило мощности, правило произведения, правило частного и многие другие.
Калькулятор производных также предоставляет пошаговые решения, которые могут помочь пользователям понять процесс расчета производных. Это может быть особенно полезно для студентов, изучающих исчисление и нуждающихся в практике решения задач и понимания правил и формул, используемых при дифференцировании.
В целом, калькулятор производных — это простой в использовании и эффективный инструмент, который поможет вам быстро и точно рассчитать производные. Используя этот инструмент, вы можете сэкономить время и сосредоточиться на понимании концепций, лежащих в основе дифференцирования, вместо того, чтобы тратить часы на вычисление производных вручную.
Как найти производный калькулятор с шагами?
Калькулятор деривативов найти в сети несложно. Вы можете либо ввести полный URL-адрес этогокалькулятор дифференцирования в поисковой системе или вы можете выполнить поиск в Google по его названию. Вы можете выполнить поиск в Google с помощью «калькулятора производной» или «калькулятора обратной производной», и вы найдете наш новейший и точный онлайн-инструмент.
Как использовать производный калькулятор с шагами?
Нашдифференцировать калькулятор очень прост в эксплуатации, так как вам необходимо следовать приведенной ниже процедуре:
- Напишите свое уравнение в первом поле ввода или загрузите любое уравнение, нажав на кнопку.
- Выберите переменную, которую вы хотите дифференцировать.
- Выберите, сколько раз вы хотите различать.
- Нажать на «РАССЧИТАТЬ» кнопка.
Сразу после нажатия на кнопку расчета наш калькулятор дифференцирования решит ваше уравнение и предоставит подробные результаты. Эти результаты помогут вам понять и изучить концепцию, практикуясь во время выполнения.
Часто задаваемые вопросы
Как дифференцировать функцию f(x)=5,4x+2,4?
Дифференцирование с обеих сторон по «х»
Таким образом, мы можем дифференцировать эту простую функцию вручную. Кроме того, мы также можем выделить калькулятор функций для онлайн-расчетов.
Как вычислить производную функции?
Чтобы вычислить производную функции, необходимо выполнить следующие шаги:
- Помните, что производная — это расчет скорости изменения функции.
- Примените производную к функции по независимой переменной, участвующей в функции.
- Упростите функцию, чтобы получить точное значение производной.
Эту же процедуру использоваликалькулятор деривативов рассчитать скорость изменения функции онлайн.
Что такое производная х?
Производная x равна 1. Она относится к результату, полученному путем дифференцирования x различными способами. Нахождение скорости изменения функции включает в себя процесс дифференцирования. Таким образом, вы можете найти калькулятор производной для этого процесса.
Какова производная от cos2(x)?
Производная cos2(x) равна,
$ frac (cos^2x) ;=; -2 cos(x) cdot sin(x) ;=; -sin^2x $
Производная cos2x — это производная тригонометрической функции, которая несколько сложна для студентов, которые не могут запомнить тригонометрические тождества. Для таких студентов решатель производных является отличным инструментом для вычисления производной тригонометрической функции.
Как отличить бывшего?
Поскольку производная экспоненциальной функции с основанием «e» равна ex, дифференцирование e в степени x эквивалентно самому e в степени x. Математически это записывается как d/dx (ex) = ex.
Это можно оценить в решателе дифференцирования для перекрестной проверки ответа и его шагов в Интернете.
Источник: calculator-derivative.com