
Корзина
Программирование
Разработка ПО
Алгоритм — создание программ и игр самостоятельно
Разработчик: Трофимов Иван Васильевич
Создайте программу для себя или своего бизнеса!Алгоритм — среда для создания программ и игр пользователями, не имеющими навыков программирования.
Версии программы Алгоритм — создание программ и игр самостоятельно
Алгоритм — создание программ и игр самостоятельно 2.7.1
Новое в версии:
— Программа стала бесплатной, с открытым кодом (https://github.com/AlexVTro/Algorithm)
— Исправлены некоторые ошибки
Операционная система: Windows XP, Windows 2000, Windows 2003 Server, Windows 2000 Server, Windows, Windows Vista, Windows 2008 Server, Windows 7, Windows 8, Windows 2012 Server, Windows 8.1, Windows 10
Алгоритм — создание программ и игр самостоятельно 2.7.1
Пожертвовать на развитие программы 1200.00 руб.
Узнаём системные требования любой игры.
Лицензия: Поддержать проект
Скриншоты Алгоритм — создание программ и игр самостоятельно
 |
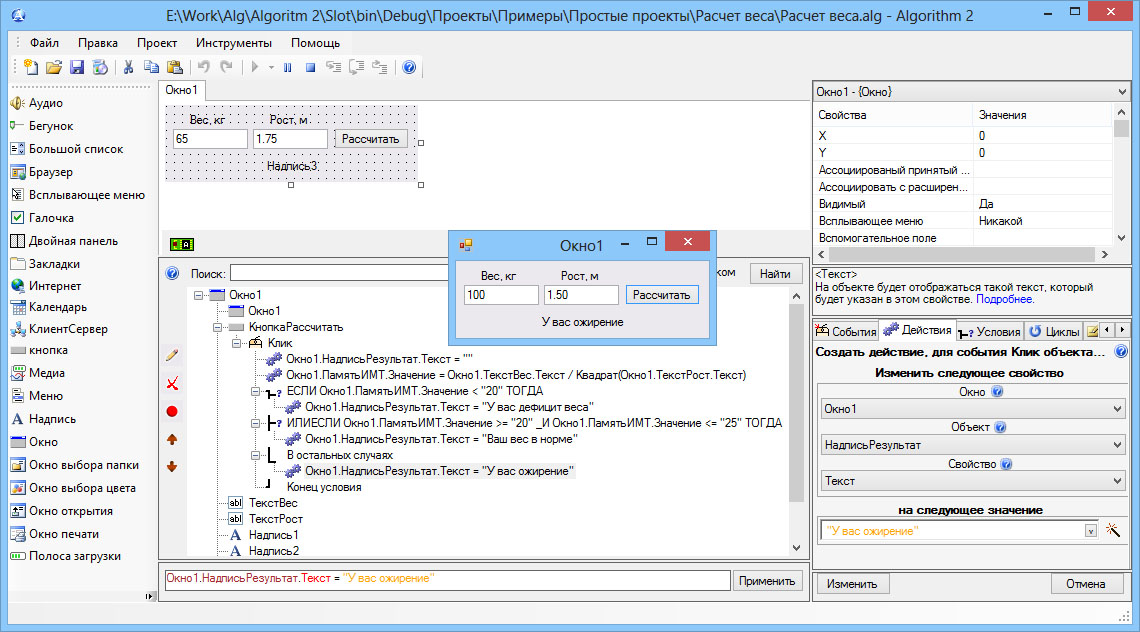 |
 |
Источник: programsmarket.ru
Программа «Алгоритм — создание программ и игр самостоятельно»
описание, версии, покупка, информация, цены, скриншоты

Создайте программу для себя или своего бизнеса!Алгоритм — среда для создания программ и игр пользователями, не имеющими навыков программирования.
Алгоритм — создание программ и игр самостоятельно
Список версий программы
Алгоритм — создание программ и игр самостоятельно 2.7
Новое в версии:
— ExcelAccess поддержка
— Автоматическое обновление программы.
— Раздел Ответы на все вопросы, помагающий в любых ситуациях в процессе создания собственной программы.
— Оптимизация программы под Windows 8, Windows 8.1.

Поддерживаемые операционные системы: Windows XP, Windows 2000, Windows 2003 Server, Windows 2000 Server, Windows Vista, Windows 2008 Server, Windows 7, Windows 8, Windows 2012 Server, Windows 8.1
Expo-Gamer: Программа Для Анализа Системных Требований Игровых Новинок
Цены
- Одна покупка на все ваши домашниерабочие компьютеры1190.00 руб. Максимальная версия с ограниченной технической поддержкой
- Одна покупка на все ваши домашниерабочие компьютеры2990.00 руб. Неограниченная версия с неограниченной технической поддержкой
Источник: www.orinksoft.ru
Системные требования алгоритмов

Различные алгоритмы могут требовать различного количества ресурсов вычислительной системы, на которых они реализованы:
· оперативной памяти (под промежуточные данные);
· постоянной памяти (под код программы и константы);
В целом, эти требования зависят от сложности и «интеллектуальности» алгоритма. Общая тенденция такова: чем эффективнее и универсальнее алгоритм, тем большие требования к вычислительным ресурсам он предъявляет. Тем не менее, в специфических случаях простые и компактные алгоритмы могут работать не хуже сложных и универсальных. Системные требования определяют их потребительские качества: чем менее требователен алгоритм, тем на более простой, а следовательно, компактной, надёжной и дешёвой системе он может быть реализован.
Так как алгоритмы сжатия и восстановления работают в паре, имеет значение соотношение системных требований к ним. Нередко можно усложнив один алгоритм значительно упростить другой. Таким образом, возможны три варианта:
Алгоритм сжатия требует больших вычислительных ресурсов, нежели алгоритм восстановления.
Это наиболее распространённое соотношение, характерное для случаев, когда однократно сжатые данные будут использоваться многократно. В качестве примера можно привести цифровые аудио- и видеопроигрыватели.
Алгоритмы сжатия и восстановления требуют приблизительно равных вычислительных ресурсов.
Наиболее приемлемый вариант для линий связи, когда сжатие и восстановление происходит однократно на двух её концах (например, в цифровой телефонии).
Алгоритм сжатия существенно менее требователен, чем алгоритм восстановления.
Такая ситуация характерна для случаев, когда процедура сжатия реализуется простым, часто портативным устройством, для которого объём доступных ресурсов весьма критичен, например, космический аппарат или большая распределённая сеть датчиков. Это могут быть также данные, распаковка которых требуется в очень малом проценте случаев, например запись камер видеонаблюдения.
Алгоритмы сжатия данных неизвестного формата
Имеется два основных подхода к сжатию данных неизвестного формата.
· На каждом шаге алгоритма сжатия очередной сжимаемый символ либо помещается в выходной буфер сжимающего кодера как есть (со специальным флагом, помечающим, что он не был сжат), либо группа из нескольких сжимаемых символов заменяется ссылкой на совпадающую с ней группу из уже закодированных символов. Поскольку восстановление сжатых таким образом данных выполняется очень быстро, такой подход часто используется для создания самораспаковывающихся программ.
· Для каждой сжимаемой последовательности символов однократно либо в каждый момент времени собирается статистика её встречаемости в кодируемых данных. На основе этой статистики вычисляется вероятность значения очередного кодируемого символа (либо последовательности символов). После этого применяется та или иная разновидность энтропийного кодирования, например, арифметическое кодирование или кодирование Хаффмана, для представления часто встречающихся последовательностей короткими кодовыми словами, а редко встречающихся — более длинными.
Код Хаффмана
Определение 1: Пусть A=1,a2,. ,an> — алфавит из n различных символов, W=1,w2,. ,wn> — соответствующий ему набор положительных целых весов. Тогда набор бинарных кодов C=1,c2,. ,cn>, такой что:
| (1) | ci не является префиксом для cj, при i!=j |
| (2) |  |
минимальна (|ci| длина кода ci) |
называется минимально-избыточным префиксным кодом или иначе кодом Хаффмана.
Замечания:
1. Свойство (1) называется свойством префиксности. Оно позволяет однозначно декодировать коды переменной длины.
2. Сумму в свойстве (2) можно трактовать как размер закодированных данных в битах. На практике это очень удобно, т.к. позволяет оценить степень сжатия не прибегая непосредственно к кодированию.
3. В дальнейшем, чтобы избежать недоразумений, под кодом будем понимать битовую строку определенной длины, а под минимально-избыточным кодом или кодом Хаффмана — множество кодов (битовых строк), соответствующих определенным символам и обладающих определенными свойствами.
Известно, что любому бинарному префиксному коду соответствует определенное бинарное дерево.
Определение 2: Бинарное дерево, соответствующее коду Хаффмана, будем называть деревом Хаффмана.
Задача построения кода Хаффмана равносильна задаче построения соответствующего ему дерева. Приведем общую схему построения дерева Хаффмана:
1. Составим список кодируемых символов (при этом будем рассматривать каждый символ как одноэлементное бинарное дерево, вес которого равен весу символа).
2. Из списка выберем 2 узла с наименьшим весом.
3. Сформируем новый узел и присоединим к нему, в качестве дочерних, два узла выбранных из списка. При этом вес сформированного узла положим равным сумме весов дочерних узлов.
4. Добавим сформированный узел к списку.
5. Если в списке больше одного узла, то повторить 2-5.
Приведем пример: построим дерево Хаффмана для сообщения S=»A H F B H C E H E H C E A H D C E E H H H C H H H D E G H G G E H C H H».
Для начала введем несколько обозначений:
1. Символы кодируемого алфавита будем выделять жирным шрифтом: A, B, C.
2. Веса узлов будем обозначать нижними индексами: A5, B3, C7.
3. Составные узлы будем заключать в скобки: ((A5+B3)8+C7)15.
1. A2 B1 C5 D2 E7 F1 G3 H15
2. A2 C5 D2 E7 G3 H15 (F1+B1)2
3. C5 E7 G3 H15 (F1+B1)2 (A2+D2)4
4. C5 E7 H15 (A2+D2)4 ((F1+B1)2+G3)5
В списке, как и требовалось, остался всего один узел. Дерево Хаффмана построено. Теперь запишем его в более привычном для нас виде.
Источник: megaobuchalka.ru