Программа 6 класса математика список тем

6 класс полностью посвящен изучению основ алгебры. Изучается делимость чисел, а также такие понятия как наибольший общий делитель и наименьшее общее кратное. Углубляются знания в области обыкновенных дробей. Изучается сложение и вычитание обыкновенных дробей с разными знаменателями. К тому же школьники учатся умножать и делить обыкновенные дроби.

Помимо натуральных чисел в 6 классе вводятся отрицательные числа, а также изучаются основные арифметические действия с ними. Особняком стоит раздел решения линейных уравнений с одной неизвестной. Он является центральной темой изучения математики в 6 классе.

Ниже представлены темы программы по математике 6 класса. Каждая тема написана репетитором по математике с нашего сайта и содержит развернутый ответ по данной теме с примерами и пояснениями.

Источник: nado5.ru

Математика 6 класс темы уроков

Математика 6 класс (Урок№1 — Повторение материала по темам «Обыкновенные дроби» и «Смешанные дроби»)

В математике 6 класса темы уроков посвящают характерным чертам делимости, делению, умножению, вычитанию и сложению рациональных и натуральных чисел и дробей с различными знаменателями. Изучают положительные и отрицательные числа, а также операции с ними. Заканчивают исследованием координат на плоскости. Кроме того, посвящают время на изучение круга и шара. 6 класс – последний год для математики, поэтому он является подготовкой к алгебре и геометрии.

Делимость чисел

В первую очередь проходят признаки делимости, делители и кратные. Эти знания помогут при решении последующих сложных задач. Можно выделить такие этапы изучения материала:

• Делители, множители и кратные
• Нечётные и чётные числа
• Простые и составные числа.
• Разложение на простые множители и отличия различных способов
• Главная теорема арифметики. Деление на 0 и 10, деление нуля
• Характерные черты делимости на 10, на 5 и на 2
• Характерные черты делимости на 9 и на 3
• Использование нескольких признаков делимости
• Наибольший общий делитель
• Наименьшее общее кратное

Вычитание и сложение дробей с отличающимися знаменателями

Программа 6 класса математика список тем

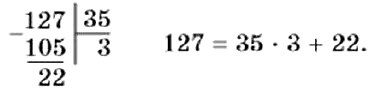
1. Если натуральное число а делится на натуральное число b, то а называют кратным b, а b — делителем а. Это означает, что а = bq, где q — натуральное число. Например, 62 кратно 31, 31 — делитель 62, так как 62 = 31 • 2.
2. Простым числом называется такое натуральное число, которое имеет только два делителя — единицу и само это число. Составным числом называется такое натуральное число, которое имеет более двух делителей.

Например, числа 2, 7, 43, 109 — простые, а числа 4, 12, 35 — составные. Число 1 не является ни простым, ни составным. Всякое составное число можно разложить на простые множители, и притом единственным способом. Например, 630 = 2 • 32 • 5 • 7.

Пропорция. Основное свойство пропорции. 6 класс.

1. Чтобы найти наименьшее общее кратное (НОК) нескольких чисел, надо разложить эти числа на простые множители и найти произведение всех получившихся простых множителей, взяв каждый из них с наибольшим показателем. Например, 72 = 2 3 • 3 2 ; 180 = 2 2 • 3 2 • 5 и 600 = 2 3 • 3 • 5 2 . Наименьшее общее кратное чисел 72, 180 и 600 равно 2 3 • 3 2 • 5 2 = 1800.

Чтобы найти наибольший общий делитель (НОД) нескольких чисел, надо разложить эти числа на простые множители и найти произведение общих простых множителей, взяв каждый из них с наименьшим показателем. Например, наибольший общий делитель чисел 72, 180 и 600 равен 2 2 • 3, т. е. числу 12.

1. Если число оканчивается цифрой 0 или цифрой 5, то оно делится на 5. Если число оканчивается любой другой цифрой, то оно не делится на 5.

• Если число оканчивается чётной цифрой, то оно делится на 2. Если число оканчивается нечётной цифрой, то оно не делится на 2.
• Если сумма цифр числа делится на 3, то и число делится на 3. Если сумма цифр числа не делится на 3, то число не делится на 3.
• Если сумма цифр числа делится на 9, то и число делится на 9. Если сумма цифр числа не делится на 9, то и число не делится на 9.

Обыкновенные дроби

1. Правильной дробью называется дробь, у которой числитель меньше знаменателя. Неправильной дробью называется дробь, у которой числитель больше знаменателя или равен ему.
2. Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
3. Чтобы привести дроби к наименьшему общему знаменателю, надо найти наименьшее общее кратное знаменателей дробей; вычислить дополнительные множители, разделив наименьшее общее кратное на каждый знаменатель; умножить числитель и знаменатель каждой дроби на соответствующий дополнительный множитель. Например, приведём к наименьшему общему знаменателю дроби 1/6, 7/12, 5/18. Наименьший общий знаменатель равен 36:

1. При сложении дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби и оставляют тот же знаменатель. При вычитании дробей с одинаковыми знаменателями из числителя первой дроби вычитают числитель второй дроби и оставляют тот же знаменатель. Например,

При сложении и вычитании дробей с разными знаменателями сначала их приводят к общему знаменателю.

1. Чтобы перемножить две дроби, надо перемножить отдельно их числители и знаменатели; первое произведение сделать числителем, а второе — знаменателем. Чтобы разделить одну дробь на другую, надо делимое умножить на дробь, обратную делителю.

Например,

Десятичные дроби

1. При округлении десятичной дроби до какого-нибудь разряда все следующие за этим разрядом цифры заменяют нулями, а если они стоят после запятой, то их отбрасывают. Если первая следующая за этим разрядом цифра 5, б, 7, 8 или 9, то к последней оставшейся цифре прибавляют 1. Если первая следующая за этим разрядом цифра 0, 1, 2, 3 или 4, то последнюю оставшуюся цифру не изменяют.

Например, 4,376 ≈ 4,4; 2,8195 ≈ 2,820; 10,1425 ≈ 10,14.

1. Сложение и вычитание десятичных дробей выполняют поразрядно. При этом дроби записывают одну под другой так, чтобы запятая оказалась под запятой.

Например:

1. Чтобы умножить одну десятичную дробь на другую, надо выполнить умножение, не обращая внимания на запятые, а затем в полученном произведении отделить запятой справа столько цифр, сколько их стоит после занятой в обоих множителях вместе.

• Чтобы разделить десятичную дробь на десятичную, надо в делимом и делителе перенести запятые вправо на столько цифр, сколько их после запятой в делителе, а затем выполнить деление на натуральное число.

Например:

1. Чтобы умножить десятичную дробь на 10n , надо в этой дроби перенести запятую на n цифр вправо. Чтобы разделить десятичную дробь на 10 n , надо в этой дроби перенести запятую на n цифр влево.

Например, 8,373 • 100 = 837,3; 3,4 : 1000 = 0,0034.

Положительные и отрицательные числа

1. Модулем положительного числа и нуля называется само это число. Модулем отрицательного числа называется противоположное ему положительное число. Модуль числа а обозначают |а|. Например, |3,6| = 3,6; |0| = 0; |–2,8| = 2,8.
2. Чтобы сложить два отрицательных числа, надо сложить их модули и перед полученным результатом поставить знак «минус».

• Чтобы сложить два числа с разными знаками, надо из большего модуля вычесть меньший и перед полученным результатом поставить знак того слагаемого, модуль которого больше.
• Сумма двух противоположных чисел равна нулю.

Например, –3,4+ (–1,8) = –5,2; 2,5 + (–4,1) = –1,6; –3,6 + 3,6 = 0.

1. Чтобы из одного отрицательного числа вычесть другое, достаточно к уменьшаемому прибавить число, противоположное вычитаемому.

Например, –5 – 1,9 = –5 + (–1,9) = –6,9.

1. Чтобы перемножить два отрицательных числа, надо перемножить их модули. Чтобы перемножить два числа с разными знаками, надо перемножить их модули и перед полученным результатом поставить знак «минус».

Например, –1,2 • (–8) = 9,6; –3 • 1,2 = –3,6.

1. Чтобы разделить отрицательное число на отрицательное, надо модуль делимого разделить на модуль делителя. Чтобы разделить два числа с разными знаками, надо модуль делимого разделить на модуль делителя и перед полученным результатом поставить знак «минус».

Например, –4,8 : (–2,4) = 2; 5,5 : (–5) = –1,1.

1. Средним арифметическим нескольких чисел называется частное от деления суммы этих чисел на число слагаемых.

Пропорции

1. Равенство двух отношений называют пропорцией. Например, равенство 2,5 : 5 = 3,5 : 7 — пропорция. Числа 2,5 и 7 — крайние члены пропорции. Числа 5 и 3,5 — средние члены пропорции. Если пропорция верна, то произведение её крайних членов равно произведению средних членов. В пропорции можно менять местами крайние члены или средние члены.
2. Две величины называются прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.

• Если величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.

1. Две величины называются обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз.

• Если величины обратно пропорциональны, то отношение значений одной из величин равно обратному отношению соответствующих значений другой величины.

Свойства действий над числами

1. Переместительное свойство сложения. От перестановки слагаемых значение суммы не изменяется.

Сочетательное свойство сложения. Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего.

Переместительное свойство умножения. От перестановки множителей значение произведения не изменяется.

Сочетательное свойство умножения. Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего.

Распределительное свойство умножения. Чтобы умножить число на сумму, можно умножить это число на каждое слагаемое и сложить полученные результаты.

Преобразование выражений

1. Слагаемые, которые имеют одинаковую буквенную часть, называются подобными слагаемыми.
2. Для того чтобы привести подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.

Например, 5а – 7а + 4а = 2а.

1. Если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки.

Например, 3х + (2а – у) = 3х + 2а – у.

1. Если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки.

Например, 5а – (2х – 3y) = 5а – 2х + 3y.

Проценты

1. Процентом называется сотая часть числа. Проценты используют для сравнения двух или более чисел. Обозначаются они символом «%». С помощью процентов удобно задавать пропорции. Если мы знаем две величины из трех — процентную долю, величину целого или величину доли, — третью легко вычислить.
2. Вычисление процентов. Этот пример показывает, как найти процентную долю от количества, а именно 25% от группы в 24 человека.
3. Найти процентное соотношение двух чисел, а именно: сколько процентов составят 48 человек в группе из 112 человек?
4. Представление числа в процентах от другого числа. Из 12 учеников в классе 9 играют на музыкальных инструментах. Чтобы найти процентную долю 9 от 12, делим величину доли на величину целого и умножаем на 100.
5. Нахождение целого из процентов. 7 учеников составляют 35% класса. Чтобы узнать, сколько всего учеников в классе, делим величину доли (7) на проценты (35) и умножаем на 100.

Окружность и круг

1. Окружность — это множество всех точек плоскости, находящихся на одном и том же расстоянии от данной точки. Круг — это часть плоскости, ограниченная окружностью. Круг можно разбить на две равные половины (полукруг): это означает, что он имеет зеркальную симметрию. Отрезок, который делит его пополам, называется диаметром.
2. Элементы окружности и круга:
   Радиус (r) – любой отрезок от центра окружности до любой точки на ней.
   Диаметр (d) – любой отрезок, соединяющий две точки окружности и проходящий через ее центр (d = 2r).
   Хорда – любой отрезок, соединяющий две точки окружности.
   Сегмент – меньшая из двух частей, на которые хорда делит круг.
   Окружность – является границей круга.
   Дуга – любая непрерывная часть окружности.
   Сектор – часть круга, ограниченная двумя радиусами и дугой. Похож на ломтик пирога.
   Площадь круга – размер пространства внутри окружности.
   Касательная – прямая, проходящая ровно через одну точку окружности.
3. Для того чтобы начертить окружность, вам нужны два инструмента — циркуль и линейка. Упираем ножку циркуля в бумагу, а грифелем описываем окружность. Радиус окружности равен раствору циркуля. Линейка нужна для точного измерения радиуса. Точку, в которую упирается остриё циркуля, называют центром окружности.
4. Длина окружности прямо пропорциональна её диаметру l = πd = 2πr. При вычислениях чаще всего используют приближённое значение числа π (пи) с точностью до сотых: π ~ 3,14.
5. Площадь круга зависит от его радиуса S = πr 2

Вы смотрели: «Математика 6 класс: все темы, правила и формулы» — это краткое повторение алгебры за 6 класс (основные понятия, формулы и определения). Краткий курс: вся информация, самое главное и всё, что нужно знать вкратце.

(с) В учебных целях использованы цитаты из следующих пособий:
1) учебник для общеобразовательных учреждений «Алгебра 7 класс» (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред.

С.А. Теляковского) — М.: Просвещение.
2) Как объяснить ребенку математику : иллюстрированный справочник для родителей / Кэрол Вордерман ; пер. с англ. Ю. Лукача, Н. Беловой ; [науч. ред. А. Н. Привалов, Ю. И. Богатырева]. — М.: Манн, Иванов и Фербер.

Выберите дальнейшие действия:

• Вернуться к Списку конспектов по математике и алгебре
• Онлайн-учебник математики 6 класс УМК Мерзляк Полонский Якир (с ответами)
• Онлайн-учебник алгебры 7 кл УМК Мерзляк Полонский Якир (с ответами)
• Онлайн-учебник алгебры 7 кл УМК Макарычев (с ответами)
• Онлайн-учебник алгебры 7 кл УМК Мордкович (с ответами)

Источник: uchitel.pro