Задание. Принадлежит ли точка с координатами x и y заштрихованной области?
Вывести об этом соответствующее сообщение.
Методические указания к выполнению задания:
1. Описать заштрихованную область с помощью логического выражения, значение которого присвоить логической переменной Р.
2. Применяя метод последовательной детализации, разделить заштрихованную область на две части и задать логическим переменным, описывающим каждую часть соответственно Р1 («полукруг») и Р2 («треугольник»).
3. Заданная точка может находиться либо в одной части заштрихованной области, либо в другой, потому Р = Р1 Ú Р2
4. Описать 1-й часть области – «полукруг»:
| уравнения, ограничивающие область: | неравенства, описывающие заштрихованную область: | логическое выражение, описывающие заштрихованную область: |
| x 2 + y 2 = 4 y = 0 | x 2 + y 2 ≤ 4 y > 0 | Р1=(x 2 + y 2 ≤ 4) Ù (y > 0) |
С++: Решение задачи 59 по Абрамову
1) Задать т. М (1; 1), x = 1, y = 1
Р1 = 1 2 + 1 2 £ 4 Ù 1 > 0
2 £ 4 Ù 1 > 0
ИСТИНА Ù ИСТИНА = ИСТИНА
2) Задать т. М (0; -1), x = 0, y = -1
Р1 = 0 2 + (-1) 2 £ 4 Ù -1 > 0
1 £ 4 Ù -1 > 0
ИСТИНА Ù ЛОЖЬ = ЛОЖЬ
не принадлежит » полукругу»
5. Описать 2-й часть области – «треугольник»:
| уравнения, ограничивающие область: | неравенства, описывающие заштрихованную область: | логическое выражение, описывающие заштрихованную область: |
| y = 0 x = 0 y = x – 3 | y £ 0 x ≥ 0 y ≥ x – 3 | P2 = (y £ 0)Ù(x ≥ 0)Ù(y ≥ x — 3) |
1) Задать т. М (1; -1), x = 1, y = -1
Р2 = (-1 £ 0) Ù (1 ≥ 0) Ù (-1 ≥ 1 — 3)
ИСТИНА Ù ИСТИНА Ù ИСТИНА = ИСТИНА
2) Задать т. М (0; 1), x = 0, y = 1
Р2 = ( 1 £ 0) Ù (0 ≥ 0) Ù (1 ≥ 0 — 3)
ЛОЖЬ Ù ИСТИНА Ù ИСТИНА = ЛОЖЬ
не принадлежит » треугольнику «
Вывод проверки: логические выражения, описывающие обе части заштрихованной области, составлены правильно.
6. Для всей области переменная Р будет истинной, если Р1 либо Р2, либо обе вместе — истинны: Р = Р1 Ú Р2
Проверку логического выражения всей области выполнить самостоятельно, задавая т. М(x,y) различные координаты (точка в 1-й области, точка в 2-й области, вне заштрихованной области).
7. Вывод сообщения выполняется с помощью развилки:
ЕСЛИ Р
ТО «т. принадлежит области»
«т. не принадлежит области»
8. Выполнить задание в Excel по разработанному алгоритму (рис.7)
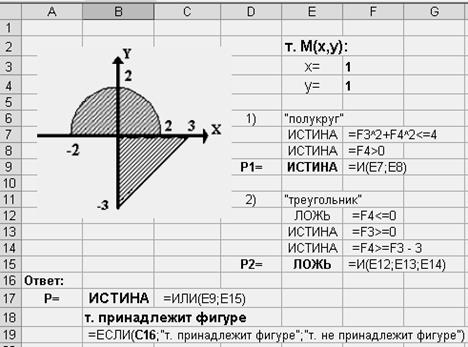
Рис. 7.
Пример выполнения задания по теме «Логические выражения»
Варианты заданий
по теме «Описание геометрического места точек»
2. Для описания отрезков (треугольников) следует вспомнить вывод уравнения прямой в отрезках:
Далее выразить y как функцию от x: y=f(x).
33 Задача: Принадлежит ли точка кругу с центром в начале координат?
2.2. Пример выполнения задания по теме «Развилки»
Задание. Вычислить заданное выражение G. Значения А и В заданы.
вариант а): вариант b):
Источник: mydocx.ru
Принадлежит ли точка заштрихованной области программа
Репутация: 571
Принадлежность точки заштрихованной области. Турбо Паскаль 7.0
Необходима программа, которая будет получать введенную координату (x и y ) и сравнивать эту координату с координатами заштрихованной области фигуры и на основании этого делать вывод о принадлежности/не принадлежности точки к заштрихованной области. Написал, программа корректно работает в пределах рисунка, но если, к примеру ввести x=100 и y=1000, она выдаст, что точка принадлежит Как задать приделы границ квадрата? Скажем, чтобы программа считала все координаты больше 3 по y и по x как невходящие. Помогите, уже идей совсем нет, похоже,что перемудрил с условиями
Program example1; Uses crt; Var x,y: real; Begin Clrscr; Writeln(‘vvedite x,y’); Readln (x,y); If ((sqr(x)+sqr(y))<=4) and (x>=-3) and (x<=3) and (y>=0) and (y<=3) then writeln(‘ne vxodit’) else writeln(‘vxodit’); readln; end.
Источник: www.tehnari.ru
Определить, попадает ли точка с заданными координатами ( x , y ) в заштрихованную область
Определить, попадает ли точка с заданными координатами ( x , y ) в заштрихованную область. Разработать алгоритм задачи и отобразить его по ГОСТ 19.701 – 90 /6/. Координаты x , y запросить функцией scanf (). Условие попадания точки в заштрихованную область записать одним предложением. Выполнить программу в режиме отладки по шагам с просмотром перехода на ветви «Да» и «Нет».
Изучить формат функции scanf (). Выполнить подробный анализ предложения объявления и инициализации. Проанализировать использованные элементы стиля программирования.
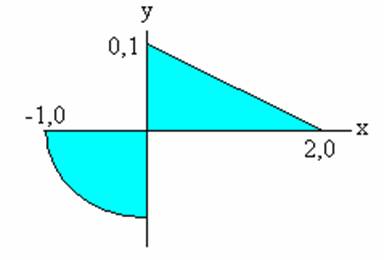
Уравнение прямой по двум точкам: Y =-1/2 X +1
Уравнение окружности: Y =
Отсюда получаем условия попадания точки в область:
Источник: dmtsoft.ru