Принадлежит ли точка плоскости программа

Для определения принадлежности точки и прямой плоскости, расположенной в пространстве, следует руководствоваться следующими ‘ положениями:

· точка принадлежит плоскости, если через нее можно провести линию, лежащую в плоскости;

· прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки;

· прямая принадлежит плоскости, если она проходит через точку данной плоскости параллельно прямой, принадлежащей этой плоскости.

Через одну точку на плоскости можно провести бесконечное множество линий. Это могут быть произвольные линии и линии, занимающие особое положение по отношению к плоскостям проекций П1 П2, П3.Прямая, принадлежащая рассматриваемой плоскости, проведенная параллельно горизонтальной плоскости проекций, называется горизонталью плоскости.

Прямая, принадлежащая рассматриваемой плоскости, проведенная параллельно фронтальной плоскости проекций, называется фронталью плоскости.

Горизонталь и фронталь являются линиями уровня.

Лекция 2. Плоскость. Точка и прямая в плоскости.

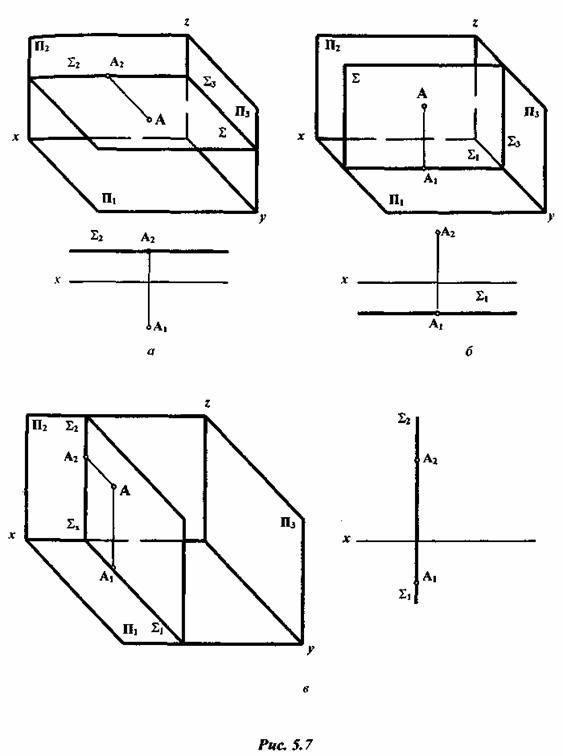
Горизонталь плоскости следует начинать строить с фронтальной проекции, т.к. она параллельна оси x, горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости.

А так как все горизонтали плоскости параллельны между собой, можно считать горизонтальный след плоскости нулевой горизонталью (рис. 5.8).

Фронталь плоскости следует начинать строить с горизонтальной проекции, т.к. она параллельна оси x, фронтальная проекция фронтали параллельна фронтальному следу. Фронтальный след плоскости -нулевая фронталь. Все фронтали плоскости параллельны между — собой (рис. 5.9).

К линии уровня относится и профильная прямая, лежащая в заданной плоскости и параллельная П3.

К главным линиям особого положения в плоскости, кроме линии уровня, относятся линии наибольшего наклонаплоскости к плоскости проекций.

Определение угла наклона плоскости

К плоскостям проекций

Плоскость общего положения, расположенная в пространстве
произвольно, наклонена к плоскостям проекций. Для определения величины двухгранного угла наклона заданной плоскости к какой-либо
плоскости проекции используются линии наибольшего наклона плоскости к плоскости проекций: к П1 — линия ската, к П2 — линия наибольшего наклона плоскости к плоскости П2.

Линии наибольшего наклона плоскости — это прямые, образующие с плоскостью проекций наибольший угол, проводятся в плоскости перпендикулярно к соответствующей линии уровня. Линии наибольшего наклона и ее соответствующая проекция образуют линейный угол, которым измеряется величина двухгранного угла, составленное данной плоскостью и плоскостью проекций (рис. 5.10).

Математика без Ху%!ни. Уравнение плоскости.

Последнее изменение этой страницы: 2016-12-10; Нарушение авторского права страницы

Рис. 3.2 Взаимное расположение прямых

Прямые в пространстве могут занимать относительно друг друга одно из трех положений:

1) быть параллельными;

Параллельными называются прямые, лежащие в одной плоскости и не имеющие общих точек.

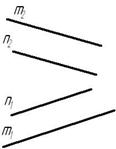
Если прямые параллельны друг другу, то на КЧ их одноименные проекции тоже параллельны (см. п. 1.2).

Пересекающимися называются прямые, лежащие в одной плоскости и имеющие одну общую точку.

У пересекающихся прямых на КЧ одноименные проекции пересекаются в проекциях точки А. Причем фронтальная () и горизонтальная ()проекции этой точки должны находиться на одной линии связи.

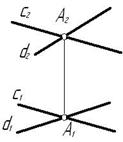
Скрещивающимися называются прямые, лежащие в параллельных плоскостях и не имеющие общих точек.

Если прямые скрещивающиеся, то на КЧ их одноименные проекции могут пересекаться, но точки пересечений одноименных проекций не будут лежать на одной линии связи.

На рис. 3.4 точка С принадлежит прямой b, а точка D – прямой а. Эти точки находятся на одинаковом расстоянии от фронтальной плоскости проекций. Аналогично точки E и F принадлежат разным прямым, но находятся на одном расстоянии от горизонтальной плоскости проекций. Поэтому на КЧ их фронтальные проекции совпадают.

Возможны два случая расположения точки относительно плоскости: точка может принадлежать плоскости или не принадлежать ей (рис. 3.5).

Признак принадлежности точки и прямой плоскости:

Точка принадлежит плоскости, если принадлежит прямой, лежащей в этой плоскости.

Прямая принадлежит плоскости, если имеет с ней две общие точки или имеет с ней одну общую точку и параллельна другой прямой, лежащей в этой плоскости.

На рис. 3.5 изображена плоскость и точки D и Е. Точка D принадлежит плоскости, т. к. принадлежит прямой l, имеющей с этой плоскостью две общие точки – 1 и А. Точка Е не принадлежит плоскости, т.к. через нее нельзя провести прямую, лежащую в данной плоскости.

На рис. 3.6 показана плоскость и прямая t, лежащая в этой плоскости, т.к. имеет с ней общую точку 1 и параллельна прямой а.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8828 — | 7538 — или читать все.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Принадлежность точки плоскости на комплексном чертеже определяется согласно аксиоме инцидентности или отношения принадлежности между элементами евклидова пространства, которая гласит: — если точка E принадлежит прямой k, а прямая k принадлежит плоскости α, то точка E принадлежит плоскости α: E ∈ k ∧ k ∈ α ⇒ E ∈ α.

Задача на принадлежность точки плоскости может быть выражена следующим образом: — заключить точку E(E`, E») в; — провести через точку E(E`, E») плоскость α общего положения

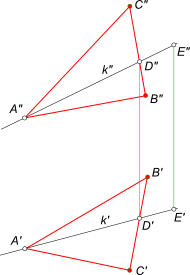
Положение плоскости α в пространстве определяется тремя точками — вершинами ΔABC. Здесь принадлежность точки плоскости α общего положения определяется ее принадлежностью прямой k, которая принадлежит плоскости α, потому что две ее точки A и D принадлежат этой плоскости. Проведя прямую в плоскости через точку E

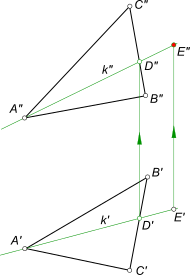
доказываем тем самым ее принадлежность заданной плоскости. Заключить точку M в плоскость α заданную параллельными прямыми a и b

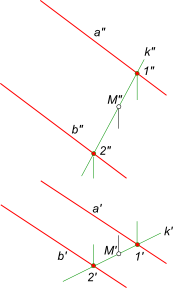
Здесь принадлежность точки плоскости α общего положения определяется ее принадлежностью прямой k, которая принадлежит плоскости α, потому что две ее точки 1 и 2 принадлежат этой плоскости. Построение искомой плоскости α: — проводим прямую через точку M; — через точки 1 и 2 взятые на прямой k проводим взаимно параллельные прямые a и b соответственно.

Через точку M провести плоскость α заданную следами

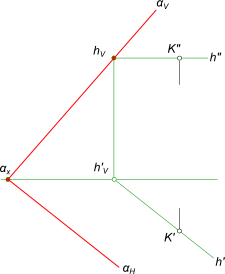
Здесь принадлежность точки плоскости α общего положения определяется ее принадлежностью прямой h, которая, в то же время, принадлежит плоскости α и является ее горизонталью. Построение искомой плоскости α: — проводим прямую h (горизонталь искомой плоскости) через точку K; — проводим горизонтальный след αH // h` ⇒ αx; — через точки αx и hV проводим фронтальный след αV.

Источник: planshet-info.ru

Определить принадлежит ли точка плоскости — Free Pascal

Здравстуйте, помогите пож-та с задачей, в паскале почти ноль, а решить как то надо, Точка с координатами (х, у) принадлежит части плоскости, лежащей между прямыми x=m, x=n, (m

Код к задаче: «Определить принадлежит ли точка плоскости»

Листинг программы

if mm) AND (x<=n) then WriteLn(‘Yes’) else writeLn(‘no’);

7 голосов , оценка 3.857 из 5

Похожие ответы

1. Определить, принадлежит ли точка заштрихованной области
2. Подпрограмма: в строке символов заменить каждую из групп стоящих рядом точек многоточием
3. Пересечение отрезков на плоскости
4. Задача на определение принадлежности точки области
5. Даны четыре точки. Определить, являются ли они вершинами параллелограмма
6. Определить, имеют ли отрезки, заданные координатами концов, общие точки
7. Определить число точек с (x;y) попадающих
8. Определить, какой минимальной длины стежка соединяет точки 1 и 2 земельного участка
9. Определить, на какой день улитка доползёт до вершины шеста?
10. Ввести x с клавиатуры и определить, сколько чисел в промежутке от 1 до 100 делятся без остатка на x, x-1 или x
11. Определить, сколько существует различных маршрутов, ведущих из левого верхнего в правый нижний угол

Все виды студенческих работ на заказ

Источник: studassistent.ru

Python-сообщество

• Начало
• » Центр помощи
• » Определить принадлежит ли точка заштрихованной части плоскости.

#1 Фев. 27, 2021 18:46:54

Определить принадлежит ли точка заштрихованной части плоскости.

Здравствуйте. Помогите, пожалуйста, решить задачу. Весь день потратил на решение, так и не смог ничего придумать.
В математике совсем не силен
Составить программу, определяющую принадлежит ли точка с координатами
(x; y) заштрихованной части плоскости. Координаты точки ввести с
клавиатуры. Для решения вам необходимо написать все уравнения прямых

Отредактировано Vasya343 (Фев. 27, 2021 18:48:36)

#2 Фев. 27, 2021 22:32:11

Определить принадлежит ли точка заштрихованной части плоскости.

Vasya343
В математике совсем не силен

дело не в математике.Перед тобой возникла какая-то проблема,и проблема она для тебя потому, что ты не знаешь как ее решить.Решение этой проблемы,этот нужный результат уже есть,и ты можешь представить в голове как ты решил эту проблему,ты видишь как ты радуешься своей победе,но не можешь вспомнить как ты пришел к этому нужному результату.Ты говоришь себе,как я это сделал. какими знаниями я обладал,которые сейчас не знаю,и это ключевой момент!Тебе нужно собрать все эти знания из которых строиться этот результат.Ты спрашиваешь себя,а что же я не знаю?

В твоем примере: что такое координаты? почитай про них если в школе не учил,интернет полон информации.
находится ли точка в заданных границах?так и пиши в поисковике “точка внутри многоугольника”, поверь от такого напора информации за раз голова может взорваться,но там знания которые приведут тебя к результату,их нужно впитать в себя,хочешь выборочно,хочешь все подряд.
Теперь когда у тебя есть нужная информация,ты можешь из нее лепить как из пластилина.Не знаешь как связать информацию или ее мало,опять ищешь, вникаешь,пробуешь,ошибаешься,снова читаешь,снова пробуешь,сравниваешь с результатом,так ты идешь к своему запланированному будущему,в котором твоя проблема решена,будущее которое ты придумал,а не которое выбрало тебя как наполнение для мира.
PS. твою задачу решали уже сотни раз. ссылка википедия

#3 Фев. 28, 2021 08:33:39

Определить принадлежит ли точка заштрихованной части плоскости.

Данную задачу нужно решать по этой формуле A x + B y + C = 0? Задача на знание разветвляющиеся процессы.

xam1816 спасибо, но по ссылке слишком мудрено, а задачка из предмета основ программирования.

Тема: Составление логических выражений. Программирование
разветвляющихся вычислительных процессов.
Цель: Научиться составлять логические выражения, использовать
условный оператор.

Отредактировано Vasya343 (Фев. 28, 2021 08:40:44)

#4 Фев. 28, 2021 11:17:11

Определить принадлежит ли точка заштрихованной части плоскости.

Vasya343
но по ссылке слишком мудрено, а задачка из предмета основ программирования.

ну тогда так
Как ты думаешь: может ли точка быть в пределах если x>6 или x < -6? или если y >6, yСоставь условия на листке бумаги, при которых точка может находится в фигуре.А когда составишь эти условия,можешь описать их средством какого-либо языка программирования.

Источник: python.su