Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.
В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.
Порядок вычисления простых выражений
В случае выражений без скобок порядок действий определяется однозначно:
- Все действия выполняются слева направо.
- В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.
Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Математика 3 класс (Урок№10 — Порядок выполнения действий в числовых выражениях.)
Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.
Условие: вычислите, сколько будет 7 − 3 + 6 .
Решение
В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:
7 − 3 + 6 = 4 + 6 = 10
Ответ: 7 − 3 + 6 = 10 .
Условие: в каком порядке нужно выполнять вычисления в выражении 6 : 2 · 8 : 3 ?
Решение
Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.
Условие: подсчитайте, сколько будет 17 − 5 · 6 : 3 − 2 + 4 : 2 .
Решение
Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:
Простой пример, в котором главное не запутаться. Порядок действий в выражениях
17 − 5 · 6 : 3 − 2 + 4 : 2 = 17 − 10 − 2 + 2
Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:
17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7
Ответ: 17 − 5 · 6 : 3 − 2 + 4 : 2 = 7 .
Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:
Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.
Что такое действия первой и второй ступени
Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.
К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.
Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:
В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).
Порядок вычислений в выражениях со скобками
Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:
Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.
Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.
Условие: вычислите, сколько будет 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 .
Решение
В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7 − 2 · 3 . Здесь нам надо умножить 2 на 3 и вычесть результат из 7 :
7 − 2 · 3 = 7 − 6 = 1
Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .
Теперь нам нужно подставить получившиеся значения в первоначальное выражение:
5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 5 + 1 · 2 : 2
Начнем с умножения и деления, потом выполним вычитание и получим:
5 + 1 · 2 : 2 = 5 + 2 : 2 = 5 + 1 = 6
На этом вычисления можно закончить.
Ответ: 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 6 .
Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.
Условие: вычислите, сколько будет 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) .
Решение
У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · ( 2 + 3 ) , а именно с 2 + 3 . Это будет 5 . Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5 . Мы помним, что сначала надо умножить, а потом сложить: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 . Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .
Ответ: 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) = 28 .
Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.
Допустим, нам надо найти, сколько будет ( 4 + ( 4 + ( 4 − 6 : 2 ) ) − 1 ) − 1 . Начинаем с выражения во внутренних скобках. Поскольку 4 − 6 : 2 = 4 − 3 = 1 , исходное выражение можно записать как ( 4 + ( 4 + 1 ) − 1 ) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению ( 4 + 5 − 1 ) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.
Разберем пример такого вычисления.
Условие: найдите, сколько будет ( 3 + 1 ) · 2 + 6 2 : 3 − 7 .
Решение
У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид ( 3 + 1 ) · 2 + 36 : 3 − 7 .
Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание.
( 3 + 1 ) · 2 + 36 : 3 − 7 = 4 · 2 + 36 : 3 − 7 = 8 + 12 − 7 = 13
Ответ: ( 3 + 1 ) · 2 + 6 2 : 3 − 7 = 13 .
В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.
Порядок действий в математике

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные операции в математике
Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше ( )
меньше (
Порядок вычисления простых выражений
Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:
- действия выполняются по порядку слева направо
- сначала выполняется умножение и деление, а затем — сложение и вычитание.
Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.
Что первое, умножение или деление? — По порядку слева направо.
Сначала умножение или сложение? — Умножаем, потом складываем.
Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Рассмотрим порядок арифметических действий в примерах.
Пример 1. Выполнить вычисление: 11- 2 + 5.
В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.
Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.
Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?
Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.
Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.
Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.
Например, в такой последовательности можно решить пример по действиям:
Действия первой и второй ступени
В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.
- Действиями первой ступени называют сложение и вычитание, а умножение и деление — действиями второй ступени.
С этими терминами правило определения порядка выполнения действий звучит так:
Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).
Порядок вычислений в выражениях со скобками
Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:
Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.
Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.
Рассмотрим порядок выполнения действий на примерах со скобками.
Пример 1. Вычислить: 10 + (8 — 2 * 3) * (12 — 4) : 2.
Как правильно решить пример:
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.
Начнем с первого 8 — 2 * 3. Что сначала, умножение или вычитание? Мы уже знаем правильный ответ: умножение, затем вычитание. Получается так:
8 — 2 * 3 = 8 — 6 = 2.
Переходим ко второму выражению в скобках 12 — 4. Здесь только одно действие – вычитание, выполняем: 12 — 4 = 8.
Подставляем полученные значения в исходное выражение:
10 + (8 — 2 * 3) * (12 — 4) : 2 = 10 + 2 * 8 : 2.
Порядок действий: умножение, деление, и только потом — сложение. Получится:
10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.
На этом все действия выполнены.
Ответ: 10 + (8 — 2 * 3) * (12 — 4) : 2 = 18.
Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.
Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).
Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:
Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:
5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.
Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.
Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции — их значения нужно вычислить до выполнения остальных действий. При этом важно учитывать правила из предыдущих пунктов, которые задают очередность действий в математике.
Другими словами, перечисленные функции по степени важности можно приравнивать к выражению в скобках.
И, как всегда, рассмотрим, как это работает на примере.
Пример 1. Вычислить (4 + 1) * 3 + 62 : 3 — 7.
В этом выражении есть степень 62. И нам нужно найти ее значение до выполнения остальных действий. Выполним возведение в степень: 62 = 36.
Подставляем полученное значение в исходное выражение:
(4 + 1) * 3 + 36 : 3 — 7.
Дальше нам уже все знакомо: выполняем действия в скобках, далее по порядку слева направо выполняем сначала умножение, деление, а затем — сложение и вычитание. Ход решения выглядит так:
(4 + 1) * 3 + 36 : 3 — 7 = 3 * 3 + 36 : 3 — 7 = 9 + 12 — 7 = 14.
Ответ: (3 + 1) * 2 + 62 : 3 — 7 = 14.
Закрепить на практике тему «Порядок действий» можно на курсах по математике в Skysmart!
Порядок действий
Для правильного вычисления значений числовых выражений, в которых нужно произвести более одного действия, необходимо знать установленный порядок выполнения арифметических действий.
Порядок действий без скобок
Установленный порядок арифметических действий без скобок:
-
Если выражение содержит только действия на сложение и вычитание, то они выполняются в порядке следования — слева направо:
Если выражение содержит только действия на умножение и деление, то действия выполняются в порядке следования — слева направо:
Если в выражении присутствуют и умножение с делением, и сложение с вычитанием, то сначала выполняются умножение и деление в порядке их следования (слева направо), а затем сложение и вычитание в порядке их следования (слева направо):
Порядок действий со скобками
Если выражение содержит скобки, то сначала выполняются все действия внутри скобок, а затем все действия, находящиеся за скобками.
В числовых выражениях со скобками порядок выполнения арифметических действий такой же, как и в выражениях без скобок.
Скобки применяются для обозначения действий, которые нужно произвести раньше остальных. Скобки не влияют на порядок остальных действий в выражении, остальные действия выполняются в указанном порядке.
Дробная черта
Дробная черта в выражении может быть заменена на знак деления, в этом случае, всё что было над и под дробной чертой надо взять в скобки. Например:
| 13 + 2 | = (13 + 2) : (10 — 7). |
| 10 — 7 |
Знак деления в выражении можно заменить дробной чертой только в том случае, если это не нарушает порядок действий. Например, выражение:
нельзя заменить на
| 20 | , |
| 4(2 + 3) |
потому что такая замена нарушит порядок действий в данном выражении.
| 20 : 4(2 + 3) ≠ | 20 | ; |
| 4(2 + 3) |
| 20 | = 20 : (4(2 + 3)). |
| 4(2 + 3) |
Дробная черта в выражении заменяет скобки и означает, что надо вычислить отдельно выражение, стоящее в числителе, и отдельно выражение, стоящее в знаменателе, и первый результат разделить на второй.
Источник: all-equa.ru
Примеры по действиям с многозначными числами для 4 класса
Подборка примеров со скобками на порядок действий для отработки вычислительных навыков.
Цель: формирование умения определять порядок выполнения действий в числовых выражениях со скобками.
Данную подборку примеров на порядок действий можно для удобства разделить на карточки по 5 штук. Чтобы достичь хороших результатов каждый день нужно решать именно такое количество. Ответы на примеры с многозначными числами даны для самоконтроля учащихся.
Ранее мы разбирали алгоритм решения примеров на порядок действий в 3-4 классе со скобками и без.
Вспомним алгоритм решения примеров на порядок действий со скобками:
Главное правило: если в примере есть скобки, то сначала выполняем действия в скобках, затем умножение и деление, и потом — сложение и вычитание начиная слева направо.
- При решении примера сначала избавьтесь от скобок.
- Вычислите и запишите полученный результат на месте скобок.
- Выполните действия по порядку.
Разберем порядок вычисления примера со скобками пошагово:
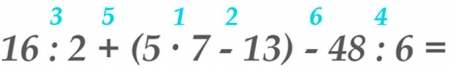
Пример
- Определим порядок действий и запишем их над арифметическими знаками.
- Найдём значение выражения, заключённого в скобках: сначала умножение или деление, потом сложение или вычитание слева направо.
- Приступим к действиям вне скобок/можно решать одновременно.
16 : 2 + (5 ⋅ 7 – 13) – 48 : 6 = 8 + (35 – 13) – 8 = 8 + 22 – 8 = 22.
Примеры на порядок действий со скобками (сложение, вычитание, умножение, деление)
Задание: расставь порядок действий и найди значение выражения.
- 9464 : 91 + (926 * 50 – 9601) =
- 3091 – 9 * (161 + 42) + 1791 =
- (349 + 636 : 6) + 9914 – 412 =
- (2340 : 5 + 932) : 50 =
- 801 + (8049 – 818) * 4 =
- 3402 + (1334 : 23 + 7026) =
- 81 * 13 + (6043 – 5711) : 2 =
- 71 * 38 + (322 * 2 + 7011) =
- (744 + 256) : 50 + 724 =
- (1561 + 2810) – (2004 + 2330 : 5) =
- 550 : (610 – 555) + 292 * 31 =
- (859 + 99) – 141 * 5 + 200 =
- 71 * 265 – (1554 : 74 + 375) =
- (2011 + 9411) + 6633 : 33 =
- 462 : (560 – 546) * 27 + 521 =
- 1908 : 12 * (1093 – 809) =
- (6105 : 5 — 450) + 613 – 105 =
- 964 + (6643 – 5963) * 155 =
- 112 * 49 – (1478 + 2411) – 322 =
- 9726 – (1430 – 86) : 42 – 2016 =
- 1390 : (528 – 518) + (9493 + 185) =
- 3012 + (3010 – 2110) * 6 + 411 =
- 8505 : 21 + (1585 – 914) : 61 =
- 351 * 0 + (1137 + 9120) : 3 =
- (7196 – 1750) + (5310 : 5 + 2822) =
- (4278 : 93 + 924 : 42) + 631 =
- 714 : 7 + (9756 – 4197) : 3 =
- (5861 + 14) : 25 + (234 + 390) =
- (1117 + 3250) – 132 * 13 =
- (96 * 214 – 14) + (4126 + 54) : 2 =
Ответы на примеры по действиям с многозначными числами:
Источник: koncpekt.ru
Контрольная работа «Примеры на порядок действий» 5 класс
После того как вы поделитесь материалом внизу появится ссылка для скачивания.
Получить код —>
Математика — еще материалы к урокам:
- Контрольная работа «Признаки делимости» 5 класс
- Контрольная работа «Площадь прямоугольника» 5 класс
- Контрольная работа «Площади и объёмы» 5 класс
- Контрольная работа «Обыкновенные дроби. Умножение и деление на 10, 100. Преобразование чисел, полученных при измерении» 5 класс
- Презентация «Использование различных приемов и методов обучения математике, способствующих развитию УУД»
- Презентация «Счёты»
Предметы
 Алгебра
Алгебра Английский язык
Английский язык Биология
Биология География
География Геометрия
Геометрия ИЗО
ИЗО Информатика
Информатика История
История Литература
Литература Математика
Математика Музыка
Музыка МХК
МХК Начальная школа
Начальная школа ОБЖ
ОБЖ Обществознание
Обществознание Окружающий мир
Окружающий мир ОРКСЭ
ОРКСЭ Педагогика
Педагогика Русский язык
Русский язык Технология
Технология Физика
Физика Физкультура
Физкультура Химия
Химия Экология
Экология
Похожие материалы
- 4-06-2017, 11:01 Контрольная работа «Порядок действий в выражениях со скобками и без»
- 29-05-2017, 22:39 Контрольная работа «Табличное умножение и деление, порядок действий
- 12-03-2017, 15:13 Контрольная работа «Употребление предлогов. Порядок слов в
- 13-07-2016, 15:23 Презентация «Порядок действий в выражениях» 2 класс
- 18-04-2016, 12:36 Разработка урока по математике в 5 классе «Порядок выполнения
- 3-08-2015, 16:38 Урок математики во 2 классе «Порядок действий в выражении»
- 1-08-2015, 10:37 Презентация «Порядок действий. Закрепление» 4 класс
- 17-07-2015, 11:50 Презентация «Порядок выполнения действий в выражениях» 3 класс
Источник: uchitelya.com