Примеры программ на рекурсию

Для решения некоторых задач рекурсия эффективнее циклов, однако она требует безошибочного кода и большего объема памяти. В противном случае возникнут ошибки или сбои во время выполнения функции. В этой статье вы узнаете о рекурсии, особенностях ее работы и увидите наглядные примеры.

Что такое рекурсия

Так называют поведение функции, когда она повторно вызывает саму себя. Рекурсия отличается от цикла тем, что не просто повторяется, а создает одну функцию внутри другой. Этот термин считается ключевым в программировании. Его можно сравнить с математической индукцией — функция выполнится после того, как получен ее результат при вызове с новыми данными.

Принцип работы рекурсии: функция А от двух запускает А от трех и т. д., пока не она достигнет завершающего условия. Они работают одновременно, а ответ выдается только после завершения последней вложенной функции и подсчета всех результатов.

Рекурсивный вызов поддерживается во всех распространенных языках программирования, включая Python, JavaScript, C. Он внедряется для решения задач, которые сложно или невозможно решить с помощью циклов.

Разбор задачи на рекурсию «Нумеролог»

• подобные решения чище и короче итерационных — вместо 40–50 строк программисту достаточно 5–10;
• подходит для выполнения крупных задач, т. к. разделяет их на части, что позволяет распараллелить задачи.

Резюмируя, рекурсивный процесс предполагает не поэтапную обработку, а деление чего-то большого на части до тех пор, пока решение не станет максимально простым.

Виды

Рекурсию подразделяют на 2 вида:

• прямая — функции вызывают сами себя, подставляя новые аргументы;
• косвенная — запуск происходит через сторонний блок кода, т. е. функция А вызывает Б, а последний снова А.

Последний вариант является менее очевидным и реже встречается. Его стоит использовать только при необходимости, т. к. такой код сложно воспринимать. Пример косвенного рекурсивного программирования:

• цикл — выполняется одно и то же действие, но много раз;
• рекурсия — функция, вызывающая саму себя с новыми аргументами.

1. Функция вызывает саму себя и приостанавливается.

2. Начинается выполнение “дочерней” и создается новый блок, который кладется поверх предыдущего. Повторение происходит вплоть до достижения останавливающего условия.

3. Функции начинают возвращать результат поэтапно и складывать их, т. е. первая выдает 1, а вторая — 2 + 1. После выполнения действия блок выходит из стека.

4. Программа выдает последний результат, полученный после завершения всех этапов.

• легко читаются — в коммерческом программировании над одним кодом работает целая команда, поэтому разработчики стараются максимально упростить его, чтобы коллеги смогли разобраться. Рекурсия получается короткой и емкой, благодаря чему проблемы с пониманием значения кода не возникнут;
• естественность — многие структуры данных и объектов ЯП рекурсивны по своей природе, например: фракталы, классовая иерархия, древовидные структуры;
• защита от ошибок — рекурсивные алгоритмы не сталкиваются с такими проблемами, как «действия выполнены в неверном порядке», «использована неинициализированная переменная».

• бесконечностью — эта частая проблема, когда не достигается базовый случай. Программа создает максимальное количество функций, зависает, а пользователь получает ошибку;
• переполнением стека — действия не выполняются, пока последний вызов не будет совершен. Из-за этого программа забирает много ресурсов, что может привести к падению производительности.

Алгоритм дифференцирует массив на 2 составляющие и выделяет 2 простых случая, которые не требуют дальнейшего упрощения, т. е. выполняется обработка всей совокупности или первая составляющая является искомой.

Примеры рекурсивных алгоритмов

Пример реального кода на JavaScript:

function look_for_key(box) < for (item in box) < if (item.is_a_box()) < look_for_key(item); >else if (item.is_a_key()) < console.log(«I found the key!») >> >

Последний вариант проще, т. к. в нем нужно найти только объект в одной из коробок. Она отражает человеческую логику — раскладываешь коробки, в которых возможно находится ключ, и осматриваешь их.

Поиск факториала

Если вам нужно посчитать факториал, на языке программирования Java это делается следующим образом:

public class Solution < public static int recursion(int n) < if (n == 1) < // Это базовый случай return 1; >return recursion(n — 1) * n; // Рекурсивный шаг > public static void main(String[] args) < System.out.println(recursion(5)); // Вызов функции >>

Палиндром

Так называют число, слово, текст, которые с разных сторон читаются одинаково, т. е. 101, топот или финское слово saippuakivikauppias. Пример определения палиндрома на Java:

public class Solution < public static String recursion(String s) < // Базовый случай if (s.length() == 1) < return «YES»; >else < if (s.substring(0, 1).equals(s.substring(s.length() — 1, s.length()))) < // Базовый случай if (s.length() == 2) < return «YES»; >// Шаг рекурсии return recursion(s.substring(1, s.length() — 1)); > else < return «NO»; >> > public static void main(String[] args) < System.out.println(recursion(«radar»)); // Вызов >>
Остались вопросы?
Укажите ваши данные, и мы вам перезвоним

Что выбрать: рекурсию или цикл

Выбор средств зависит от поставленной задачи и требований, например:

• если необходима большая скорость выполнения и минимальная нагрузка, или существует опасность перегрузки памяти — выбирают циклы;
• когда важна читаемость и лаконичность кода — рекурсию.

Последний вариант выбирают в задачах, когда нужно, например, обойти вложенные каталоги. Обычно в них есть свои переменные, асинхронные потоки. Их легче обработать, используя рекурсию, т. к. результат обхода одного каталога не влияет на итоги анализа следующего.

Также рекурсия эффективна, если функция кэшируема, т. е. запоминает данные и на следующих этапах возвращается сохраненная информация.

Выводы

Таким образом, рекурсия — функция, вызывающая сама себя. Она содержит базовый случай и передает новым уровням измененные данные. Информация хранится в стеке, поэтому возможно переполнение с последующей остановкой программы. Рекурсивные алгоритмы обычно работают медленнее итерационных, однако легче пишутся и читаются.

Источник: loftschool.com

Рекурсия в программировании. Анализ алгоритмов

Рекурсия — это свойство объекта подражать самому себе. Объект является рекурсивным если его части выглядят также как весь объект. Рекурсия очень широко применяется в математике и программировании:

• структуры данных:

• граф (в частности деревья и списки) можно рассматривать как совокупность отдельного узла и подграфа (меньшего графа);
• строка состоит из первого символа и подстроки (меньшей строки);

Статья посвящена анализу трудоемкости рекурсивных алгоритмов, приведены необходимые математические сведения, рассмотрены примеры. Кроме того, описана возможность замены рекурсии циклом, хвостовая рекурсия.

Содержание:

1. Примеры рекурсивных алгоритмов
2. Анализ рекурсивных алгоритмов

1. Метод подстановки (итераций)
2. Метод математической индукции
3. Основной метод

Примеры рекурсивных алгоритмов

Рекурсивный алгоритм всегда разбивает задачу на части, которые по своей структуре являются такими же как исходная задача, но более простыми. Для решения подзадач функция вызывается рекурсивно, а их результаты каким-либо образом объединяются. Разделение задачи происходит лишь тогда, когда ее не удается решить сразу (она является слишком сложной).

Например, задачу обработки массива нередко можно свести к обработке его частей. Деление на части выполняется до тех пор, пока они не станут элементарными, т.е. достаточно простыми чтобы получить результат без дальнейшего упрощения.

Поиск элемента массива

начало; search(array, begin, end, element) ; выполняет поиск элемента со значением element в массиве array между индексами begin и end если begin > end результат := false; элемент не найден иначе если array[begin] = element результат := true; элемент найден иначе результат := search(array, begin+1, end, element) конец; вернуть результат

Алгоритм делит исходный массив на две части — первый элемент и массив из остальных элементов. Выделяется два простых случая, когда разделение не требуется — обработаны все элементы или первый элемент является искомым.

В алгоритме поиска разделять массив можно было бы и иначе (например пополам), но это не сказалось бы на эффективности. Если массив отсортирован — то его деление пополам целесообразно, т.к. на каждом шаге количество обрабатываемых данных можно сократить на половину.

Двоичный поиск в массиве

Двоичный поиск выполняется над отсортированным массивом. На каждом шаге искомый элемент сравнивается со значением, находящимся посередине массива. В зависимости от результатов сравнения либо левая, либо правая части могут быть «отброшены».

начало; binary_search(array, begin, end, element) ; выполняет поиск элемента со значением element ; в массиве упорядоченном по возрастанию массиве array ; между индексами begin и end если begin > end конец; вернуть false — элемент не найден mid := (end + begin) div 2; вычисление индекса элемента посередине рассматриваемой части массива если array[mid] = element конец; вернуть true (элемент найден) если array[mid] < element результат := binary_search(array, mid+1, end, element) иначе результат := binary_search(array, begin, mid, element) конец; вернуть результат

Вычисление чисел Фибоначчи

Числа Фибоначчи определяются рекуррентным выражением, т.е. таким, что вычисление элемента которого выражается из предыдущих элементов: (F_0 = 0, F_1 = 1, F_n = F_ + F_, n > 2).

начало; fibonacci(number) если number = 0 конец; вернуть 0 если number = 1 конец; вернуть 1 fib_1 := fibonacci(number-1) fib_2 := fibonacci(number-2) результат := fib_1 + fib_2 конец; вернуть результат

Быстрая сортировка (quick sort)

Алгоритм быстрой сортировки на каждом шаге выбирает один из элементов (опорный) и относительно него разделяет массив на две части, которые обрабатываются рекурсивно. В одну часть помещаются элементы меньше опорного, а в другую — остальные.

Сортировка слиянием (merge sort)

В основе алгоритма сортировки слиянием лежит возможность быстрого объединения упорядоченных массивов (или списков) так, чтобы результат оказался упорядоченным. Алгоритм разделяет исходный массив на две части произвольным образом (обычно пополам), рекурсивно сортирует их и объединяет результат. Разделение происходит до тех пор, пока размер массива больше единицы, т.к. пустой массив и массив из одного элемента всегда отсортированы.

На каждом шаге слияния из обоих списков выбирается первый необработанный элемент. Элементы сравниваются, наименьший из них добавляется к результату и помечается как обработанный. Слияние происходит до тех пор, пока один из списков не окажется пуст.

начало; merge(Array1, Size1, Array2, Size2) ; исходные массивы упорядочены ; в результат формируется упорядоченный массив длины Size1+Size2 i := 0, j := 0 вечный_цикл если i >= Size1 дописать элементы от j до Size2 массива Array2 в конец результата выход из цикла если j >= Size2 дописать элементы от i до Size1 массива Array1 в конец результата выход из цикла если Array1[i] < Array2[j] результат[i+j] := Array1[i] i := i + 1 иначе (если Array1[i] >= Array2[j]) результат[i+j] := Array2[j] j := j + 1 конец; вернуть результат

Анализ рекурсивных алгоритмов

При анализе сложности циклических алгоритмов рассчитывается трудоемкость итераций и их количество в наихудшем, наилучшем и среднем случаях [4]. Однако не получится применить такой подход к рекурсивной функции, т.к. в результате будет получено рекуррентное соотношение. Например, для функции поиска элемента в массиве:

Рекуррентные отношения не позволяют нам оценить сложность — мы не можем их просто так сравнивать, а значит, и сравнивать эффективность соответствующих алгоритмов. Необходимо получить формулу, которая опишет рекуррентное отношение — универсальным способом сделать это является подбор формулы при помощи метода подстановки, а затем доказательство соответствия формулы отношению методом математической индукции.

Метод подстановки (итераций)

Заключается в последовательной замене рекуррентной части в выражении для получения новых выражений. Замена производится до тех пор, пока не получится уловить общий принцип и выразить его в виде нерекуррентной формулы. Например для поиска элемента в массиве:

Можно предположить, что (T^_n = T^_ + ktimesmathcal(1)), но тогда (T^_n = T^_ + ntimesmathcal(1) = mathcal(n)).

Рекурсия. Примеры решения задач. Преимущества и недостатки рекурсии

Любая функция (метод) в своем теле может вызывать сама себя. Рекурсия – это такой способ определения функции, при котором результат возврата из функции для данного значения аргумента определяется на основе результата возврата из той же функции для предыдущего (меньшего или большего) значения аргумента.

Если функция (метод) вызывает сам себя, то такой вызов называется рекурсивным вызовом функции. При каждом рекурсивном вызове запоминаются предыдущие значения внутренних локальных переменных и полученных параметров функции. Чтобы следующий шаг рекурсивного вызова отличался от предыдущего, значение как-минимум одного из параметров функции должно быть изменено. Остановка процесса рекурсивных вызовов функции происходит, когда изменяемый параметр достиг некоторого конечного значения, например, обработан последний элемент в массиве.

2. Объяснения к реализации задач на рекурсию. Как правильно организовать рекурсивный вызов функции?

Рекурсивное обращение к функции может быть осуществлено, если алгоритм определен рекурсивно.

Чтобы циклический процесс преобразовать в рекурсивный, нужно уметь определить (выделить) три важных момента:

• условие прекращения последовательности рекурсивных вызовов функции. Например, если счетчик или итератор с именем k изменяется от 1 до 10 в возрастающем порядке, то условие прекращения есть достижение значения k =10. Условие прекращения указывается в операторе return ;
• формулу следующего элемента или итератора, который используется в рекурсивном процессе. Эта формула указывается в операторе return ;
• список параметров, которые передаются в рекурсивную функцию. Один из параметров обязательно есть итератор (счетчик) изменяющий свое значение. Другие параметры являются дополнительными, например, ссылка на массив, над которым осуществляется обработка.

3. Поиск суммы элементов массива. Пример

По подобному примеру можно создавать собственные рекурсивные функции, которые определяют любые суммы элементов любых массивов.

Задача. Задан массив чисел A . Разработать рекурсивную функцию, которая находит сумму элементов массива:

где n – количество элементов массива. Программный код функции следующий:

// сумма элементов массива int Sum(int i, int A[], int n) < if (i==n-1) return A[i]; else return A[i]+Sum(i+1,A,n); >

Как видно из примера, в рекурсивную функцию Sum() передается 3 параметра:

• текущее значение итератора i ;
• массив A ;
• количество элементов массива n .

Выход из функции осуществляется, если будет обработан последний элемент массива. Условие прекращения рекурсивного процесса имеет вид:

if (i==n-1) return A[i];

Для суммирования текущего значения A[i] со следующими указывается строка:

return A[i]+Sum(i+1,A,n);

где рекурсивный вызов Sum(i+1, A, n) означает следующее значение массива A . Параметр i+1 указывает, что на следующем уровне вызова рекурсивной функции будет взят следующий после данного элемент массива.

Использование функции Sum() в другом программном коде может быть, например, таким:

int A[] = < 5, 7, 2, -1 >; int n = 4; int sum; sum = Sum(0,A,n); // sum = 13

4. Пример подсчета количества вхождений заданного символа в строке

В данном примере реализована рекурсивная функция Count() , которая определяет количество вхождений заданного символа c в строке s . Функция получает 3 параметра:

• символ c , который нужно сравнить с каждым символом строки s ;
• строка s ;
• дополнительная переменная i , которая есть счетчиком рекурсивного цикла.

Реализация функции Count() следующая:

// подсчет символа c в строке символов s int Count(char c, string s, int i) < if (i==s.length()) // условие окончания рекурсивного процесса — вся строка пройдена return 0; else < if (c == s[i]) // если символ найден return Count(c,s,i+1)+1; // увеличить количество найденных символов на 1 else return Count(c,s,i+1); // иначе, перейти к обработке следующего символа > >

5. Пример нахождения факториала числа – n!

Вычисление факториала числа методом рекурсии есть почти в каждом учебнике. Факториал числа вычисляется по формуле

Рекурсивный вызов можно организовать двумя способами:

• в порядке возрастания 1, 2, …, n ;
• в порядке убывания n , n -1, …, 2, 1.

В данном примере разработаны две функции, которые находят факториал обоими способами. Программный код функций следующий:

// вычисление факториала — способ 1 int Fact1(int n, int i) < if (i==n) return n; // условие завершения рекурсивного процесса else return i*Fact1(n, i+1); // переход к следующему числу i+1 > // вычисление факториала — способ 2 int Fact2(int n) < if (n==1) return 1; // условие завершения рекурсивного процесса else return n*Fact2(n-1); // переход к предыдущему числу n-1 >

В первую функцию Fact1() передаются 2 параметра. Первый параметр определяет максимально возможное значение n , которое может быть умножено. Второй параметр определяет текущее значение i которое умножается.

Во второй функции Fact2() передается 1 параметр – максимально возможное значение n , принимающее участие в рекурсивном умножении. Второго параметра здесь не нужно, поскольку условие прекращения рекурсивного процесса есть известно и равно 1. В функции Fact2() рекурсивный процесс завершается при n =1.

Использование функций в другом программном коде может быть следующим:

int f; // использование функции Fact1() f = Fact1(5,1); // f = 5! = 120 f = Fact1(7,1); // f = 7! = 5040 f = Fact1(2,1); // f = 2! = 2 // использование функции Fact2() f = Fact2(5); // f = 5! = 120 f = Fact2(8); // f = 8! = 40320

6. Программа нахождения наибольшего общего делителя (алгоритм Евклида). Пример

В примере определяется наибольший общий делитель по формуле Евклида:

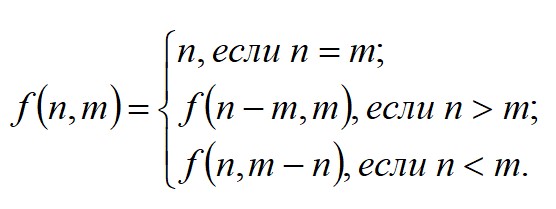
Программный код функции следующий:

// наибольший общий делитель по алгоритму Евклида int MaxDiv(int n, int m) < if (n==m) return n; else if (n>m) return MaxDiv(n-m, m); else return MaxDiv(n, m-n); >

Использование функции MaxDiv() может быть следующим:

int md; md = MaxDiv(8, 3); // md = 1 md = MaxDiv(24, 96); // md = 24 md = MaxDiv(9, 15); // md = 3

7. Подсчет количества элементов массива, больших заданного числа. Пример

Демонстрируется метод Count() , возвращающий количество элементов, больших заданного числа num . В метод передается 4 параметра:

• число num , которое нужно сравнивать с каждым элементом массива;
• массив чисел A[ ] ;
• количество элементов массива n ;
• текущее значение счетчика в массиве.

// подсчет количества элементов массива, больших заданного числа int Count(double num, double A[], int n, int i) < if (i==n) return 0; // условие окончания рекурсивного процесса else < if (numreturn Count(num, A, n, i+1) + 1; // добавить 1 к результату, и перейти далее else return Count(num, A, n, i+1); // перейти к следующему элементу массива > >

Использование метода Count() в другом методе

double A[] = < 2.8, 3.5, 1.9, 2.2, 3.6 >; int k; k = Count(2.3, A, 5, 0); // k = 3 k = Count(0.9, A, 5, 0); // k = 5

8. Преимущества использования рекурсии в программах. Пример

Рекурсию часто сравнивают с итерацией.

Организация циклического процесса с помощью рекурсии имеет свои преимущества и недостатки.

Можно выделить следующие взаимосвязанные преимущества рекурсии:

• естественность (натуральность) представления сложных, на первый взгляд, алгоритмов;
• рекурсивный алгоритм более читабелен в сравнении с итерационным;
• для многих распространенных задач рекурсию более легко реализовать чем итерацию. Рекурсия хорошо подходит для реализации алгоритмов обхода списков, деревьев, анализаторов выражений, комбинаторных задач и т.д.

Недостатки рекурсии состоят в следующем:

• по сравнению с итерацией многоразовый вызов рекурсивной функции требует больше времени. Это связано с тем, что при вызове рекурсивного метода его параметры копируются в стек. При завершении вызова рекурсивной функции предыдущие значения параметров вытягиваются из стека, что приводит к лишним операциям. Итерационный алгоритм для той же задачи работает быстрее;
• если рекурсивная функция содержит большие объемы локальных внутренних переменных и большое количество параметров, то использование рекурсии не является эффективным. Это связано с тем, что для каждого рекурсивного вызова нужно делать копии этих переменных и параметров. При большом количестве рекурсивных вызовов это приведет к чрезмерному использованию памяти.

Связанные темы

Источник: www.bestprog.net