23 июня 1912 года родился Алан Тьюринг – английский математик, логик, криптограф. Он внес большой вклад в развитие информатики , в его честь названа самая престижная в мире награда в области информатики – Премия Тьюринга . Во время Второй мировой Тьюринг активно занимался криптоанализом , в том числе криптоанализом немецкого шифратора Enigma (на портале Эрудит.Онлайн есть конкурс по криптографии «Энигма» ).
В этой статье остановимся подробнее на машине Тьюринга и попытаемся объяснить ее работу максимально простым языком.
Машина Тьюринга
Машина Тьюринга – это абстрактная вычислительная машина . Если совсем просто, то машина Тьюринга – это воображаемый компьютер с бесконечной памятью.
Художественное представление машины Тьюринга
Формально машина состоит из бесконечной ленты и управляющего устройства , которое может считывать и записывать символы в ячейки ленты. Управляющее устройство может двигаться влево и вправо по ленте.
Для чего это нужно?
Тьюринг предложил эту модель для формализации понятия алгоритма . То есть считается, что задачу можно решить с помощью некоторого алгоритма тогда и только тогда, когда ее решение можно представить в виде программы для машины Тьюринга (эта гипотеза называется тезисом Чёрча — Тьюринга).
Машина Тьюринга. Введение. Понятие машины тьюринга. Решение задачи
Так как устройство машины довольно простое, то, очевидно, что каждый шаг в такой программе должен быть элементарен.
Как работает машина Тьюринга?
Шаг машины можно представить так:
- Управляющее устройство , указывающее на конкретную ячейку на ленте, считывает значение в этой ячейке.
- По правилам, которые заданы заранее для решения задачи, управляющее устройство может изменить символ в ячейке (а может и не менять), а затем остаться на месте или сдвинуться на соседнюю ячейку вправо или влево. Также может измениться состояние управляющего устройства (а может и остаться прежним).
У управляющего устройства есть отдельный параметр, который называется состоянием . Набор таких состояний задается для каждой конкретной программы свой, но обязательно в этом наборе есть начальное состояние (в котором машина начинает работать) и конечные состояния (когда мы считаем, что программа завершилась, и машина останавливается). Эти состояния меняются в соответствии с правилами , которые заранее заданы.
Как записать простейшую программу?
Программа задается набором правил , которые еще называют правилами перехода. Для записи этих правил нет какого-то единого языка, поэтому в нашей статье запишем их в виде таблицы.
Итак, в качестве входных данных у нас есть последовательность символов 0 и 1 , и мы будем называть ее входным словом . Для простоты мы будем считать, что управляющее устройство указывает на первый слева символ нашего слова (если управляющее устройство указывает на произвольный символ слова, то эта проблема легко решается, но сейчас пропустим этот момент).
Источник: dzen.ru
Машина Тьюринга
В 1936 г. Аланом Тьюрингом для уточнения понятия алгоритма был предложен абстрактный универсальный исполнитель. Его абстрактность заключается в том, что он представляет собой логическую вычислительную конструкцию, а не реальную вычислительную машину. Термин «универсальный исполнитель» говорит о том, что данный исполнитель может имитировать любой другой исполнитель. Например, операции, которые выполняют реальные вычислительные машины можно имитировать на универсальном исполнителе. В последствие, придуманная Тьюрингом вычислительная конструкция была названа машиной Тьюринга.
Кроме того, предполагается, что универсальный исполнитель должен уметь доказывать существование или отсутствие алгоритма для той или иной задачи.
Что собой представляет машина Тьюринга?
Машина Тьюринга состоит из бесконечной в обе стороны ленты, разделенной на ячейки, и автомата (головки), которая управляется программой.
Программы для машин Тьюринга записываются в виде таблицы, где первые столбец и строка содержат буквы внешнего алфавита и возможные внутренние состояния автомата (внутренний алфавит). Содержимое таблицы представляет собой команды для машины Тьюринга. Буква, которую считывает головка в ячейке (над которой она находится в данный момент), и внутренне состояние головки определяют, какую команду нужно выполнить. Команда определяется пересечением символов внешнего и внутреннего алфавитов в таблице.
Чтобы задать конкретную машину Тьюринга, требуется описать для нее следующие составляющие:
- Внешний алфавит. Конечное множество (например, А), элементы которого называются буквами (символами). Одна из букв этого алфавита (например, а0) должна представлять собой пустой символ.
- Внутренний алфавит. Конечное множество состояний головки (автомата). Одно из состояний (например, q1) должно быть начальным (запускающим программу). Еще одно из состояний (q0) должно быть конечным (завершающим программу) – состояние останова.
- Таблица переходов. Описание поведения автомата (головки) в зависимости от состояния и считанного символа.
Автомат машины Тьюринга в процессе своей работы может выполнять следующие действия:
- Записывать символ внешнего алфавита в ячейку (в том числе и пустой), заменяя находившийся в ней (в том числе и пустой).
- Передвигаться на одну ячейку влево или вправо.
- Менять свое внутреннее состояние.
Одна команда для машины Тьюринга как раз и представляет собой конкретную комбинацию этих трех составляющих: указаний, какой символ записать в ячейку (над которой стоит автомат), куда передвинуться и в какое состояние перейти. Хотя команда может содержать и не все составляющие (например, не менять символ, не передвигаться или не менять внутреннего состояния).
Пример работы машины Тьюринга
Допустим, на ленте есть слово, состоящее из символов #, $, 1 и 0. Требуется заменить все символы # и $ на нули. В момент запуска головка находится над первой буквой слова слева. Завершается программа тогда, когда головка оказывается над пустым символом после самой правой буквы слова.
Примечание: длина слова и последовательность символов значения не имеют. На рисунке приводится пример последовательности выполнения команд для конкретного случая. Если на ленте будет другое слово, то и последовательность выполнения команд будет другой. Несмотря на это, данная программа для машины Тьюринга (на рисунке – таблица слева) применима к любым словам описанного внешнего алфавита (соблюдается свойство применимости алгоритма ко всем однотипным задачам – массовость).
Можно усложнить программу. Допустим, головка располагается не обязательно над первым, а над любым символом слова. Тогда программа для данной машины Тьюринга может быть такой (а могла бы быть и другой):
Здесь происходит сдвиг головки влево до тех пор, пока она не окажется над пустым символом. После этого машина переходит в состояние q2 (команды которого совпадают с командами q1 предыдущей программы).
Источник: inf1.info
Примеры программ для машины тьюринга
 8 марта, 2014
8 марта, 2014  Andrey K
Andrey K
(50 голос, значение: 3,92 из 5)

Один из важнейших вопросов современной информатики — существует ли формальный исполнитель, с помощью которого можно имитировать любого формального исполнителя. ответ на этот вопрос был получен почти одновременно двумя выдающимися учеными — А. Тьюрингом и Э. Постом. Предложенные ими исполнители отличались друг от друга, но оказалось, что они могут имитировать друг друга, а главное — имитировать работу любого формального исполнителя.
Что такое формальный исполнитель? Что значит — один формальный исполнитель имитирует работу другого формального исполнителя? Если Вы играли в компьютерные игры — на экране объекты беспрекословно подчиняются командам играющего. Каждый объект обладает набором допустимых команд. В то же время компьютер сам является исполнителем, причем не виртуальным, а реальным.
Вот и получается, что один формальный исполнитель имитирует работу другого формального исполнителя.
Рассмотрим работу Машины Тьюринга.
Машина Тьюринга представляет собой бесконечную ленту, поделенную на ячейки, и каретку (считывающе-печатающее устройство), которая движется вдоль ленты.
Таким образом Машина Тьюринга формально описывается набором двух алфавитов:
A= — внешний алфавит, служит для записи исходных данных
Q= — внутренний алфавит, описывает набор состояний считывающе-печатного устройства.

Каждая ячейка ленты может содержать символ из внешнего алфавита A = (В нашем случае A=)
Допустимые действия Машины Тьюринга таковы:
1) записать какой-либо символ внешнего алфавита в ячейку ленты (символ, бывший там до того, затирается)
2) сместиться в соседнюю ячейку
3) сменить состояние на одно из обозначенных символом внутреннего алфавита Q
Машина Тьюринга — это автомат, который управляется таблицей.
Строки в таблице соответствуют символам выбранного алфавита A, а столбцы — состояниям автомата Q = . В начале работы машина Тьюринга находится в состоянии q1. Состояние q0 — это конечное состояние, попав в него, автомат заканчивает работу.
В каждой клетке таблицы, соответствующей некоторому символу ai и некоторому состоянию qj, находится команда, состоящая из трех частей
· символ из алфавита A
· направление перемещения: «>» (вправо), « · новое состояние автомата

В приведенной выше таблице алфавит A = (содержит 3 символа), а внутренний алфавит Q=, q0 — состояние, заставляющее каретку остановиться.
Рассмотрим несколько задач решением. Скачать машину Тьюринга Вы можете на сайте в разделе СКАЧАТЬ.
Задача 1. Пусть A=. На ленте в ячейках находятся символы из алфавита в следующем порядке 0011011. каретка находится над первым символом. Необходимо составить программу, которая заменит 0 на 1, 1 на 0 и вернет каретку в первоначальное положение.
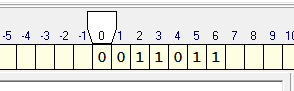
Теперь определимся с состояниями каретки. Я называю их — «желания каретки что-то сделать».
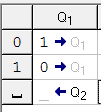
q1) Каретка должна пойти вправо: если видит 0 меняет его на 1 и остается в состоянии q1, если видит 1 — меняет его на 0 и остается в состоянии q1, если видит _ — ворачивается назад на 1 ячейку «желает что-то другое», т.е переходит в состояние q2. Запишем наши рассуждения в таблицу исполнителя. Синтаксис смотрите в справке к программе)
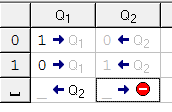
q2) Теперь опишем «желание каретки» q2. Мы должны вернуться в первоначальное положение. Для этого: если видим 1 оставляем ее и остаемся в состоянии q2 (с тем же желанием дойти до конца ряда символов); если видим 0 — оставляем его и продолжаем двигаться влево в состоянии q2; видим _ — сдвигается вправо на 1 ячейку. Вот вы оказались там, где требуется в условии задачи. переходим в состояние q0.
Посмотреть работу программы можно на видео:
Задача 2. Дано: конечная последовательность 0 и 1 (001101011101). Необходимо выписать их после данной последовательности, через пустую ячейку, а в данной последовательности заменить их на 0. Например:
Из 001101011101 получим 000000000000 1111111.
Как видите, семь единиц записались после данной последовательности, а на их местах стоят нолики.
Приступим к рассуждениям. Определим, какие состояния необходимы каретке и сколько.
q1) увидел 1 — исправь на нолик и перейди в другое состояние q2 (новое состояние вводится, чтобы каретка не поменяла на нули все единицы за один проход)
q2) ничего не менять, двигаться к концу последовательности
q3) как только каретка увидела пустую ячейку, она делает шаг вправо и рисует единичку, если она видит единичку — то движется дальше, чтобы подписать символ в конце. Как только нарисовал единицу, переходим в состояние q4
q4) проходим по написанным единицам, ничего не меняя. Как только доходим до пустой ячейки, разделяющей последовательность от единиц, переходим с новое состояние q5
q5) в этом состоянии идем начало последовательности, ничего не меняя. Доходим до пустой ячейки, разворачиваемся и переходим в состояние q1
Состояние q0 каретка примет в том случае, когда она пройдет в состоянии q1 до конца данной последовательности и встретит пустую ячейку.
Получим такую программу:
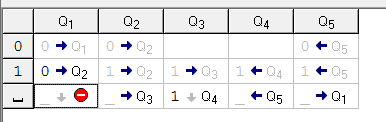
Работу Машины Тьюринга можете посмотреть на видео ниже.
(50 голос, значение: 3,92 из 5)
 Опубликовано в рубрике Теория и практика
Опубликовано в рубрике Теория и практика  Метки: алгоритмы, Машина Тьюринга, практическая работа
Метки: алгоритмы, Машина Тьюринга, практическая работа
Источник: krivaksin.ru