A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?
Cancel Create
ProgrammingManual / 4 / Лекция-4.md
- Go to file T
- Go to line L
- Copy path
- Copy permalink
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
Cannot retrieve contributors at this time
365 lines (274 sloc) 28.2 KB
- Open with Desktop
- View raw
- Copy raw contents Copy raw contents Copy raw contents
Copy raw contents
Использование программами компьютерной памяти
Полезный материал на эту тему в четком изложении имеется также здесь
Компьютерная программа, как последовательность машинных инструкций, представленная в памяти, сама по себе является пассивной, в этом смысле она не отличается от обычных данных.
Цикл с предусловием | Информатика Паскаль #15 | Инфоурок
В противоположность этому, программу которая исполняется на компьютере, называют процессом. Процесс характеризуется используемым адресным пространством памяти (и его содержимым), используемыми глобальными переменными, используемыми регистрами процессора, состоянием стека, открытыми файлами и так далее.
Дополнительно, о том, что такое процесс в вычислительной системе, можно посмотреть, например, здесь
Каждому процессу операционна система (ОС) выделяет своё собственноё виртуальное адресное пространство, начинающееся с нулевого байта, и заканчивающееся N-ым (число N — зависит от конкретной архитектуры компьтера).
В каждой ОС существует механизм трансляции (отображеия) виртуального адресного пространства в адресное пространство физической памяти таким образом, чтобы на компьютере одновременно могло выполняться множество различных процессов. При этом наличие виртуального адресного пространства позволяет мыслить процесс так, как будто бы он один владеет всей памятью компьтера. Не вдаваясь в подробности, отметим, что для реализации этого механизма используется так называемая страничная организация памяти.
Использование концепции виртуальной памяти в вычислительной сиситеме дает следующие преимущества
- освобождает программиста от необходимости вручную управлять загрузкой частей программы в память и согласовывать использование памяти с другими программами
- позволяет предоставлять программам больше памяти, чем физически установлено в системе (за счет использования дискового пространства, т.е. за счет так называемого свопинга)
- в многозадачных системах (таких как Windows, Linux) позволяет изолировать друг от друга одновременно выполняющиеся программы, путём назначения им непересекающихся адресных пространств
Дополнительно о концепции виртуальной памяти можно посмотреть, например, здесь
Виртуальное адресное пространство любого процесса подразделяется на:
- сегмент программного кода (в котором размещается двоичный код программы), непрерывно занимающий область пямяти с младшими адресами
- затем, следующую в порядке увеличения значений адресов, область статических данных
- затем, следующую в порядке увеличения значений адресов, область так называемой динамической памяти (или, по-другому, — кучи)
- старшие адреса виртуальной памяти занимает так называемый аппаратный стек (стек вызовов).
Циклы. Цикл while. Что это. Что делает. Пример. Синтаксис. Урок #14.
Графичестки виртуальную память компьютера, которая с логической точки зрения представляет собой одномерный массив байтов, можно пердставить так
Здесь имеется в виду, что каждый байт памяти имеет адрес, т.е. свой порядеовый номер, и на рисунке эти адреса увеличиваются снизу вверх.
Стек вызовов используется для размещения в нем локальных переменных функций. При вызове любой подпрограммы на вершину стека помещаются ее локальные переменные, а также — так называемый адрес возврата, по которому находится очередная инструкция программы, вызвавшей данную подпрограму. После завершения этой подпрограммы, соответствующие ей данные немедленно убираются с вершины стека. На самом деле просто указатель стека (это эдрес вершины стека), содержащийся в специальном регистре процессора, увеличиватся на соответствующую величину. А при вызове очередной подпрограммы и помещении на вершину стека очередной порции данных, указатель стека уменьшается (стек растет в сторону уменьшения адресов).
Стек также называют автоматической памятью, потому что описанный процесс использования стека происходит автоматически, и программисту, если только он не программирует на ассемблере, не нужно для этого ничего делать.
В статической памяти располагаются, в частности, данные соответствующие глобальным переменным (или только ссылкам на них: поскольку в языке Julia переменные динамические, то нет возможности сами их зачения помщать в статическую память).
В свою очередь, динамическая память может захватываться процессом по мере необходимости. Например, в динамической памяти размещают массивы, размеры которых заранее не были известны.
Стек имеет ограниченный размер (фактический предельный размер стека определяеися ОС), поэтому программисту необходимо заботиться о предотвращении переполнения стека. Чаще всего переполнение стека возникает при неправильном использовании рекурсии. Рекурсия — это когда, например, некоторая функция в своем теле осуществляет вызов самой себя.
В языке Julia (как и в Python, но только не в C/C++) реализован механизм так называемой автоматической сборки мусора, который автоматически освобождает фрагменты динамической памяти, после того как программа утрачивает ссылки на на эти фрагменты. Например,
r=Robot() r=0
здесь после второго присваивания ссылка на объект типа Robot будет утрачена.
Автоматическая сборка мусора исключает так называемую утечку памяти — очень неприятный эффект, возможный при программировании на языках, где управлеине памятью возлагается на программиста (как, например, в C/C++), если только программист допустит соответствующую ошибку.
Простейшие приемы доказательства и контроля правильности программного кода
Промежуточные утверждения
Каждая подпрограмма или даже просто участок кода предполагаю свое условие «ДАНО» и условие «РЕЗУЛЬТАТ». Поэтому если программный код включает последовательный вызов подпрограмм (или просто логически законченных участков код), то в промежутки между ними целесообразно включать комментарии, содержащие соответствующие утверждения.
Поэтому, если подпрограммы (или просто последовательные участки кода) работают правильно, то доказательство правильности всей программы сведется просто к прочтению этих утверждений.
Или, например, если требуется проверить, что Робот находится в юго-западном углу, то в соответствующее место программы нужно поместить
Если такого рода условия окажутся выполнеными, то выполнение программы просто будет продолжено. В противном же случае произойдет прерывание вычислительного процесса, и о том, что проверяемое условие не было выполнено, будет выведено сообщение.
Циклы
Участки кода программы, закрученые в циклы, зачастую бывают не столь простыми для анализа. Поэтому для анализа циклических участков кода требуются особый метод.
Cвойство цикла с предусловием
Для любого цикла с предусловием верно:
while Условие_продолжения_цикла == true . end #УТВ: Условие_продолжения_цикла == false
Инвариант цикла и метод доказательства правильности цикллического алгоритма
Инвариантом цикла с предусловием называется какое-либо условие (предикат), которое имеет значение true перед началом выполнения этого цикла и после любого числа его повторений.
Для того, чтобы инвариант цикла мог быть использован для доказательства правильности циклического алгоритма, он должен быть составлен подходящим для этого образом.
Пример использования инварианта в доказательстве правильности алгоритма: замаркировать ряд от начала до конца
function mark_beg_end(r,side) # — маркировать от начала до конца putmarker!(r) #ИНВАРИАНТ: В клетке с Роботм и во всех передыдущих (по ходу движения) стоят маркеры while isborder(r,aide)==false move!(r,side) putmarker!(r) end #УТВ: Робот — в последней (по ходу движения) клетке end
Имеем доказательство правильности алгоритма:
ИНВАРИАНТ УТВ => весь ряд замаркирован от начала до конца
function mark_beg_end(r,side) # — маркировать от начала до конца #ИНВАРИАНТ: Во всех передыдущих (по ходу движения) клетках стоят маркеры while isborder(r,aide)==false putmarker!(r) move!(r,side) end #УТВ: Робот — в последней (по ходу движения) клетке putmarker!(r) end
Имеем тоже самое доказательство правильности алгоритма: ИНВАРИАНТ УТВ => весь ряд замаркирован от начала до конца
Но, с точки зрения следования принципу повторного использования кода, лучше было бы так
mark_beg_end(r,side) = (putmarker!(r); putmarkers!(r,side))
function putmarkers!(r,side) #ИНВАРИАНТ: Во всех передыдущих (по ходу движения) клетках, за исключением начальной, стоят маркеры while isborder(r,side)==false move!(r,side) putmarker!(r) end end
ЗАМЕЧАНИЕ. Если в теле цикла с предусловием имеются операторы break или return , то они могут нарушать «естественный» порядок выполнения операторов, составляющих тело этого цикла, и, следовательно, метод доказательства правильности такого цикла на основе инварианта цикла будет не применим. Точно также для цикла с постусловием понятие инварианта цикла не работает.
Опасность и нежелательность цикла с постусловием*
В языке Julia, как и в языке Python специальной конструкции «цикл с постусловием», нет, но вот, например, в языке C/C++ она есть:
do . while(Условие_продолжения_цикла == true)
Но в Julia такой цикл тоже можно организовать
while true . if Условие_продолжения_цикла == false break end end
Но такие циклы таят в себе следующую опастность. Пусть, например, Робот находится на некотором удалении от перегородки на востотке и требуется переместить Робота вплотную к этой перегородке.
С помощью цикла с предусловием решение запищется так:
while isborder(r,Ost)==false move!(r,Ost) end
И это, очевидно, будет правильно во ВСЕХ возможных случаях. А вот если мы попытаемся записать решение с помощью цикла с постусловием, т.е. так:
while true move!(r,Ost) if isborder(r,Ost) == true break end end
то получимм код, который правильно работает во вех случаях КРОМЕ одного, а именно, кроме случая, когда Робот изначально стоит рядом с перегородкой. Опасность такого кода состоит в том, что его многократно можно тестировать и не обнаружить никакой ошибки, но она есть (!), и может проявиться в самый не подходящий момент.
Ровно та же ситуация возникает и во многих других подобных случаях. Пусть, например, требуется возвести число 2 в целую неотрицательную степень n.
С помощью цикла с предусловием это запишется так:
# n — заданое целое неотрицательное число p=1 while n>0 n -= 1 p *= 2 end #УТВ: p=2^n
А вот использование цикла с постусловием и в этом случае может породить ошибку:
# n — заданое целое неотрицательное число p=1 while true n -= 1 p *= 2 if n0 break end end #УТВ: p=2^n при n>0, НО ТОЛЛЬКО НЕ ПРИ n=0 (!)
При n=0 вместо требуемой 1 получится 2 (!).
Вывод: циклом с постусловием лучше всего никогда не пользоваться.
Пример: алгоритм подсчёта числа перегородок в ряду
Пусть требуется решить следующую задачу.
ДАНО: Робот — у западной или восточной границы не самого северного ряда. На поле имеются прямолинейные горизонтальные перегородки, не примыкающие к внешней рамке.
РЕЗУЛЬТАТ: Робот — противоположной грагицы поля и функция возвращает число горизонтальных перегородок, находящихся непосредственно над рядом с роботом
Поскольку перегородки могут иметь разную длину, то необходимо договориься, когда следует увеличивать счетчик числа перегородок: при обнаружении начал или концов этих перегородок. Допустим мы решили считать начала перегородок. Как обнаружить начало?
Тут очень просто, если сверху от Робота пергородки нет, а после перемещения Робота в соседнюю клетку она появилась, то надо увеличивать счетчик числа перегородо. A если сверху от Робота перегородка была, то независимо от ситуации после его перемещения делать будет ничего не надо. Т.е. действия будут зависеть от ситуации, которая была на предыдущем шаге соответствующего цикла.
Метод переменной состояния
Для фиксации этой ситуации можно использовать специальную переменную, в которой будет храниться соответствующее логическое значение.
Эту переменную назовем state, т.к. в ней будет фиксироваться состояние нашего алгоритма. Переменную, принимающую логические значения также обычно называют «флагом».
function num_borders(r::Robot,side::HorizonSide) state = false # по условию у границы перегородки сверху быть не может num=0 #ИНВАРИАНТ: num = число ранее (по ходу движения) обнаруженных перегородок while move!(r,side)==false move!(r,side) if state==false if isborder(r,Nord)==true num += 1 state = true end end end #УТВ: Робот — в конце ряда (следовательно, больше в этом ряду необнаруженных перегородок нет) return num end
Альтернативный способ
В этом решении состояние алгоритма фиксировалось в специальной переменной, однако для фиксации состояния можно обойтись и без перемнной. А именно, можно использовать две вспомогательные функции: пойти_промежуток и пройти_мимо_перегородки, и две ити функции выполнять в цикле поочередно в указанном порядке, пока не будет достигнут конец ряда. Тогда во время выполнения первой из вспомогательных функций алгороитм будет находиться в одном состоянии, а при выполнении второй функции, алгоритм будет находиься во втором состоянии. Вот реализация этой идеи.
function num_borders(r::Robot,side::HorizonSide) num=0 while isborder(r,side)==false if попытка_пройти_промежуток(r,side) = true #УТВ: Робот в начале очередной перегородки num += 1 пройти_мимо_перегородки(r,side) end end return num end function попытка_пройти_промежуток(r::Robot,side::HorizonSide) while isborder(r,Nord)==false if isborder(r,side) = true return false end move!(r,side) e end return true end пройти_мимо_перегородки(r::Robot,side::HorizonSide) = while isborder(r,Nord)==true move!(r,side) end
Источник: github.com
Цикл с предусловием
Рассмотренный цикл forвыполняет необходимую функциональность, когда число повторений тела цикла известно к моменту его начала. Однако часто приходится решать задачи, когда число повторений цикла заранее неизвестно. В ряде ситуаций это значение определяется по мере выполнения вычислительных действий. И тогда применяют другую разновидность цикла — цикл с условием. В языке предусмотрено два цикла с условием:
- условие цикла проверяется перед циклом (цикл с предусловием);
- условие цикла проверяется после цикла (цикл с постусловием).
На языке блок-схем цикл с предусловием показан на рис. 2.11. Здесь все организуется с помощью уже известных элементов. На языке C/C++ такая схема реализуется с использованием следующей синтаксической конструкции: while (логическое условие ) < тело цикла >Так же, как и при использовании цикла for без фигурных скобок можно использоватьтолько один оператор.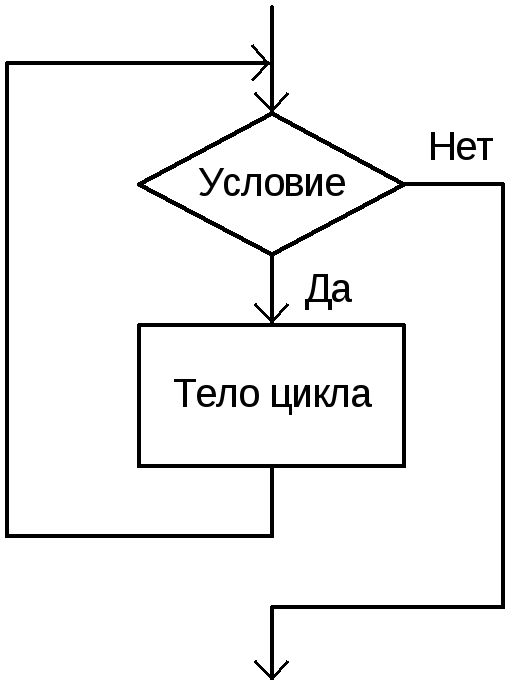 
Факториалом целого положительного числа N называется произведение всех целых чисел от 1 до N включительно. Условие задания таково: необходимо найти наименьшее целое положительное число, факториал которого не меньше 10 15 . Программное решение данной задачи приведено в листинге 2.14, а соответствующая блок-схема показана на рис. 2.12. Листинг 2.14. Пример использования цикла с предусловием #include using namespace std; #include #include void main() < int N; float Fact,A=1.0E+15; N=1; Fact=1; while (Fact < A ) < N=N+1; Fact= Fact*N; >cout cout _getch(); >
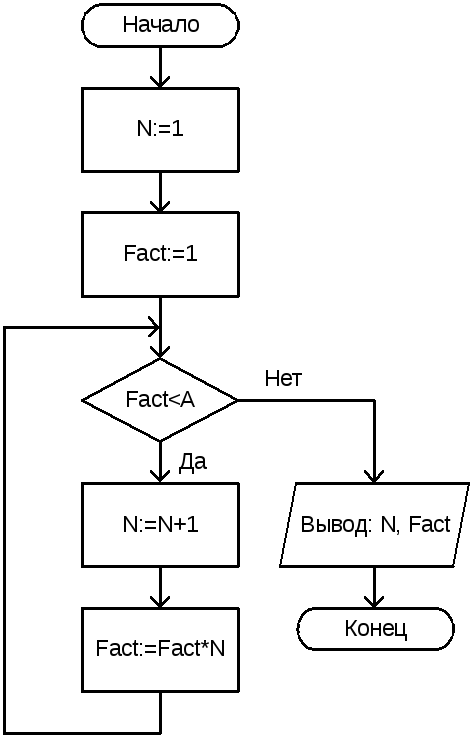Рис. 2.12. Блок-схема к программе листинга 2.14
Цикл с постусловием
В этом случае условие проверяется после цикла. Цикл повторяется до тех пор, пока проверка указанного условия будет давать результат «ложь», т. е. пока условие не выполнено. Важно отметить, что если условие сразу окажется истинным, то цикл все равно выполняется один раз. Блок-схема цикла с постусловием показана на рис. 2.13.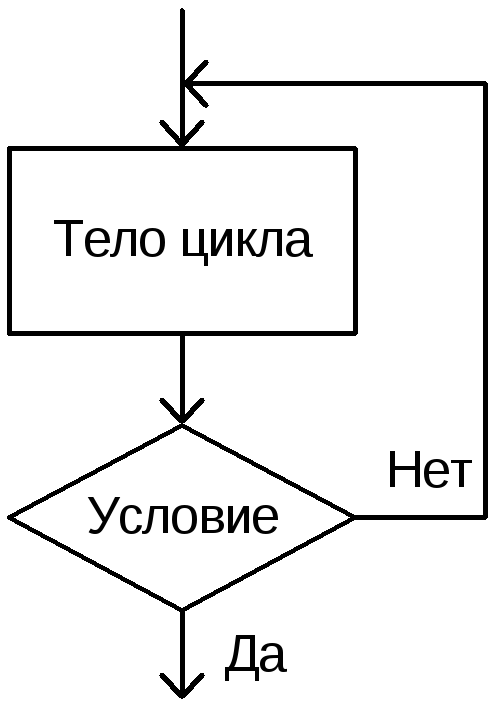 
Рис.
2.13. Блок-схема с постусловием Для цикла с постусловием сначала выполняется тело цикла, а затем управление передается на проверку условия. В зависимости от истинности или ложности условия тело цикла выполняется повторно или же происходит переход к оператору, следующему за телом цикла.
Основное различие двух рассмотренных вариантов циклов с условием: цикл с постусловием гарантированно выполняется хотя бы раз, а цикл с пред- условием может быть не выполнен ни разу, если условие сразу же окажется ложным. Выполнение цикла с постусловием продолжается, если проверка логического условия дает ложный результат.
Если же логическое условие выполняется, то происходит выход из цикла. На языке данный тип цикла реализуется с помощью следующей синтаксической конструкции: do < тело цикла >while ( логическое выражение); Рассмотрим пример, в котором пользователю предоставляется возможность ввода с клавиатуры целых чисел и их суммирования.
При вводе нуля суммирование заканчивается и на экране отображается результат. Блок-схема алгоритма показана на рис. 2.14, а текст программы приведен в листинге 2.15.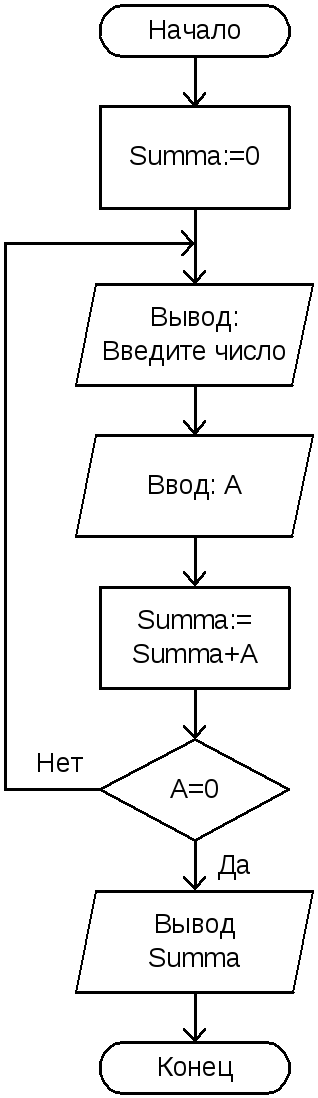 
Рис. 2.14. Блок-схема к программе листинга 2.15 Листинг 2.15.
Пример использования цикла с постусловием #include using namespace std; #include #include void main() < float Summa,A; Summa=0; do < cout >A; Summa=Summa+A; > while (A > 0 ); cout _getch(); > Метки В большинстве случаев алгоритмы требуют организации программных переходов. Такие переходы можно реализовать и с использованием уже рассмотренных ранее ресурсов.
Однако в C/C++ имеетсяоператор безусловного перехода, который весьма полезен на начальном этапе изучения программирования. Синтаксис оператора выглядит так: goto метка; В этом операторе ключевую роль играет метка— произвольный идентификатор, позволяющий именовать определенный оператор в программе. После метки необходимо поставить двоеточие.
В листинге 2.16 приведен текст программы, которая позволяет вычислить произведение чисел, вводимых с клавиатуры. При вводе нуля в качестве очередного числа программа завершает работу, а результат выводится на экран. Листинг 2.16. Пример использования меток в программе #include using namespace std; #include #include void main() < float Mul,A; Mul=1; M1: cout > A; if (A==0) goto M2; Mul= Mul*A; goto M1; M2: cout
Источник: studfile.net
Управляющие операторы языка
Операторы цикла используются для вычислений, повторяющихся многократно. В Паскале имеется три вида циклов: цикл с предусловием while , цикл с постусловием repeat и цикл с параметром for . Каждый из них состоит из определенной последовательности операторов.
Блок, ради выполнения которого и организуется цикл, называется телом цикла. Остальные операторы служат для управления процессом повторения вычислений: это начальные установки, проверка условия продолжения цикла и модификация параметра цикла ( рис. 2.5). Один проход цикла называется итерацией.
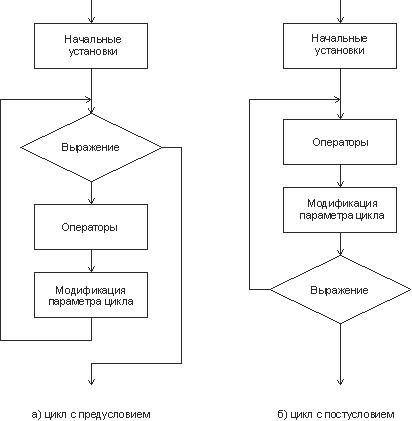
Рис. 2.5. Структурные схемы операторов цикла
Начальные установки служат для того, чтобы до входа в цикл задать значения переменных, которые в нем используются.
Проверка условия продолжения цикла выполняется на каждой итерации либо до тела цикла (тогда говорят о цикле с предусловием, см. рис. 2.5, а ), либо после тела цикла (цикл с постусловием, см. рис. 2.5, б ). Разница между ними состоит в том, что тело цикла с постусловием всегда выполняется хотя бы один раз, после чего проверяется, надо ли его выполнять еще раз. Проверка необходимости выполнения цикла с предусловием делается до тела цикла, поэтому возможно, что он не выполнится ни разу.
Параметром цикла называется переменная, которая используется при проверке условия цикла и принудительно изменяется на каждой итерации, причем, как правило, на одну и ту же величину. Если параметр цикла целочисленный, он называется счетчиком цикла. Количество повторений такого цикла можно определить заранее. Параметр есть не у всякого цикла. В так называемом итеративном цикле условие продолжения содержит переменные, значения которых изменяются в цикле по рекуррентным формулам 1 Рекуррентной называется формула, в которой новое значение переменной вычисляется с использованием ее предыдущего значения. .
Цикл завершается, если условие его продолжения не выполняется. Возможно принудительное завершение как текущей итерации, так и цикла в целом. Для этого служат операторы break , continue и goto . Передавать управление извне внутрь цикла не рекомендуется, потому что при этом могут не выполниться начальные установки.
Цикл с предусловием while
Формат оператора прост:
while выражение do оператор
Выражение должно быть логического типа. Например, это может быть операция отношения или просто логическая переменная. Если результат вычисления выражения равен true , выполняется расположенный после служебного слова do простой или составной оператор (напомню, что составной оператор заключается между begin и end ). Эти действия повторяются до того момента, пока результатом выражения не станет значение false . После окончания цикла управление передается на следующий за ним оператор.
ВНИМАНИЕ Если в теле цикла необходимо выполнить более одного оператора, необходимо заключить их в блок с помощью ключевых слов begin и end .
Пример. Программа, печатающая таблицу значений функции
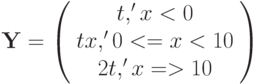
для аргумента, изменяющегося в заданных пределах с заданным шагом.
Опишем алгоритм в словесной форме.
- Ввести исходные данные.
- Взять первое значение аргумента.
- Определить, какому из интервалов оно принадлежит.
- Вычислить значение функции по соответствующей формуле.
- Вывести строку таблицы.
- Перейти к следующему значению аргумента.
- Если оно не превышает конечное значение, повторить шаги 3–6, иначе закончить.
Шаги 3–6 повторяются многократно, поэтому для их выполнения надо организовать цикл. Назовем необходимые нам переменные так: начальное значение аргумента — Xn , конечное значение аргумента — Xk , шаг изменения аргумента — dX , параметр — t . Все величины вещественные. Программа выводит таблицу, состоящую из двух столбцов — значений аргумента и соответствующих им значений функции ( пример 2.2).
program tabl_fun; var Xn, Xk : real; < начальное и конечное значение аргумента >dX : real; < шаг изменения аргумента >x, y : real; < текущие значения аргумента и функции >t : real; < параметр >begin writeln(‘Введите Xn, Xk, dX, t’); < приглашение ко вводу данных >readln(Xn, Xk, dX, t); < ввод исходных данных – шаг 1 >writeln(‘ ————————— ‘); < заголовок таблицы >writeln(‘| X | Y |’); writeln(‘ ————————— ‘); x := Xn; < первое значение аргумента = Xn – шаг 2 >while x if x < 0 then y := t; < вычисление значения функции — шаг 4 >if (x >= 0) and (x < 10) then y := t * x; < шаг 4 >if x >= 10 then y := 2 * t; < шаг 4 >writeln(‘|’, x:9:2,’ |’, y:9:2,’ |’); < вывод строки табл. – шаг 5 >x := x + dX; < переход к следующему значению аргумента — шаг 6 >end; writeln(‘ ————————— ‘); end.
Листинг 2.2. Таблица значений функции (оператор while)
Параметром этого цикла, то есть переменной, управляющей его выполнением, является х . Для правильной работы цикла необходимо присвоить параметру начальное значение до входа в цикл (шаг 2). Блок модификации параметра цикла представлен оператором, выполняющимся на шаге 6. Для перехода к следующему значению аргумента текущее значение наращивается на величину шага и заносится в ту же переменную.
Цикл с постусловием repeat
Тело цикла с постусловием заключено между служебными словами repeat и until , поэтому заключать его в блок не требуется.
repeat тело цикла until выражение
В отличие от цикла while , этот цикл будет выполняться, пока логическое выражение после слова until ложно. Как только результат выражения станет истинным, произойдет выход из цикла. Вычисление выражения выполняется в конце каждой итерации цикла.
Этот вид цикла применяется в тех случаях, когда тело цикла необходимо обязательно выполнить хотя бы один раз: например, если в цикле вводятся данные и выполняется их проверка.
Пример. Программа, вычисляющая квадратный корень вещественного аргумента X с заданной точностью eps по итерационной формуле:
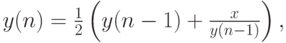
где y ( n –1) — предыдущее приближение к корню (в начале вычислений выбирается произвольно), y ( n ) — последующее приближение. Процесс вычислений прекращается, когда приближения станут отличаться друг от друга по абсолютной величине менее, чем на eps — величину заданной точности ( пример 2.3)..
program square_root; var X, eps, < аргумент и точность >Yp, Y : real; < предыдущее и последующее приближение >begin repeat writeln(‘Введите аргумент и точность (больше нуля): ‘); readln(X, eps); until (X > 0) and (eps > 0); Y := 1; repeat Yp := Y; Y := (Yp + X / Yp) / 2; until abs(Y — Yp) < eps; writeln(‘Корень из ‘, X:6:3, ‘ с точноcтью ‘, eps:7:5, ‘равен ‘, Y:9:5); end.
Источник: intuit.ru