1. На ленте машины Тьюринга содержится последовательность символов “+”. Напишите программу для машины Тьюринга, которая каждый второй символ “+” заменит на “–”. Замена начинается с правого конца последовательности. Автомат в состоянии q 1 обозревает один из символов указанной последовательности. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
2. Дано число n в восьмеричной системе счисления. Разработать машину Тьюринга, которая увеличивала бы заданное число n на 1. Автомат в состоянии q 1 обозревает некую цифру входного слова. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
3. Дана десятичная запись натурального числа n > 1. Разработать машину Тьюринга, которая уменьшала бы заданное число n на 1. Автомат в состоянии q 1 обозревает правую цифру числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
4. Дано натуральное число n > 1. Разработать машину Тьюринга, которая уменьшала бы заданное число n на 1, при этом в выходном слове старшая цифра не должна быть 0. Например, если входным словом было “100”, то выходным словом должно быть “99”, а не “099”. Автомат в состоянии q 1 обозревает правую цифру числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
Машина Тьюринга. Введение. Понятие машины тьюринга. Решение задачи
5. Дан массив из открывающих и закрывающих скобок. Построить машину Тьюринга, которая удаляла бы пары взаимных скобок, т.е. расположенных подряд “()”.
Например, дано “) (() (()”, надо получить “). ((”.
Автомат в состоянии q 1 обозревает крайний левый символ строки. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
6. Дана строка из букв “ a ” и “ b ”. Разработать машину Тьюринга, которая переместит все буквы “ a ” в левую, а буквы “ b ” — в правую части строки. Автомат в состоянии q 1 обозревает крайний левый символ строки. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
7. На ленте машины Тьюринга находится число, записанное в десятичной системе счисления. Умножить это число на 2. Автомат в состоянии q 1 обозревает крайнюю левую цифру числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
8. Даны два натуральных числа m и n, представленные в унарной системе счисления. Соответствующие наборы символов “|” разделены пустой клеткой. Автомат в состоянии q 1обозревает самый правый символ входной последовательности. Разработать машину Тьюринга, которая на ленте оставит сумму чисел m и n. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
9. Даны два натуральных числа m и n, представленных в унарной системе счисления. Соответствующие наборы символов “|” разделены пустой клеткой. Автомат в состоянии q 1 обозревает самый правый символ входной последовательности. Разработать машину Тьюринга, которая на ленте оставит разность чисел m и n. Известно, что m > n.
Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
10. На ленте машины Тьюринга находится десятичное число. Определить, делится ли это число на 5 без остатка. Если делится, то записать справа от числа слово “да”, иначе — “нет”. Автомат обозревает некую цифру входного числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.
Решения заданий
В состоянии q 1 машина ищет правый конец числа, в состоянии q 2 — пропускает знак “+”, при достижении конца последовательности — останавливается. В состоянии q 3машина знак “+” заменяет на знак “–”, при достижении конца последовательности она останавливается.
Задача 2
Решение этой задачи аналогично рассмотренному выше примеру.
Задача 3
Состояние q 1 — уменьшаем младшую (очередную) цифру на 1. Если она не равна нулю, то после уменьшения сразу — останов, если же младшая цифра равна 0, то вместо нее пишем 9, смещаемся влево и вновь выполняем вычитание. В клетку [ a 0, q 1] машина Тьюринга никогда не попадет, поэтому ее можно не заполнять.
Задача 4 (усложнение задачи 3)
Состояние q 1 — уменьшаем младшую (очередную) цифру на 1. Если она больше 1, то после уменьшения — сразу останов, если же младшая цифра равна 0, то вместо нее пишем 9, смещаемся влево и вновь выполняем вычитание. Если уменьшаемая цифра равна 1, то вместо нее пишем 0 и переходим в состояние q 2.
Состояние q 2 — после записи “0” в каком-либо разряде надо проанализировать, не является ли этот ноль старшей незначащей цифрой (т.е. не стоит ли слева от него в записи выходного слова a 0).
Состояние q 3 — если записанный “0” является старшей незначащей цифрой, то его надо удалить из записи выходного слова.
Те клетки, в которые машина Тьюринга никогда не попадает, оставляем пустыми.
Задача 5
Состояние q 1: если встретили “(”, то сдвиг вправо и переход в состояние q 2; если встретили “ a 0”, то останов.
Состояние q 2: анализ символа “(” на парность, в случае парности должны увидеть “)”. Если парная, то возврат влево и переход в состояние q 3.
Состояние q 3: стираем сначала “(”, затем “)” и переходим в q 1.
Задача 6
Решение этой задачи обычно вызывает у школьников затруднение. При разборе решения этой задачи можно пойти, например, следующим путем.
Рассмотрите со школьниками следующие варианты входных слов и попросите их сформулировать, что должна делать машина Тьюринга, каков внешний вид выходного слова, чем с точки зрения машины Тьюринга эти варианты различаются:
aaa —> выходное слово совпадает с входным, просматриваем входное слово до тех пор, пока оно не заканчивается.
a —> выходное слово совпадает с входным, просматриваем входное слово до тех пор, пока оно не заканчивается.
bbb —> выходное слово совпадает с входным, просматриваем входное слово до тех пор, пока оно не заканчивается.
b —> выходное слово совпадает с входным, просматриваем входное слово до тех пор, пока оно не заканчивается.
ab —> выходное слово совпадает с входным, просматриваем входное слово до тех пор, пока оно не заканчивается.
Результат обсуждения. Машина Тьюринга должна “понимать”, по цепочке каких букв она идет, т.е. у нее должно быть как минимум два состояния. Пусть состояние q 1 — движение по цепочке из букв “ a ”, а q 2 — состояние движения по цепочке из букв “ b ”. Заметим, что цепочка может состоять и из одной буквы. Если мы дошли до конца строки в состоянии q 1 или q 2, т.е. встретили a 0, машина должна остановиться, мы обработали всю строку.
Рассмотрим следующие варианты входных слов:
bba —> abb
bbbaab —> aabbbb
aabbbaab —> aaaabbbb
Результат обсуждения. Первый вариант входного слова можно последовательно обработать следующим образом: bba —> bbb —> вернуться к левому концу цепочки из букв “ b ” —> abb (заменить первую букву в этой цепочке на “ a ”). Для выполнения этих действий нам потребуется ввести два новых состояния и, кроме того, уточнить состояние q 2. Таким образом, для решения этой задачи нам нужно построить машину Тьюринга со следующими состояниями:
q 1 — идем вправо по цепочке букв “ a ”. Если цепочка заканчивается a 0, то переходим в q 0; если заканчивается буквой “ b ”, то переходим в q 2;
q 2 — идем вправо по цепочке букв “ b ”, если цепочка заканчивается a 0, то переходим в q 0; если заканчивается “ a ”, то заменяем букву “ a ” на “ b ”, переходим в состояние q 3(цепочку вида заменили на цепочку вида );
q 3 — идем влево по цепочке букв “ b ” до ее левого конца. Если встретили a 0 или “ a ”, то переходим в q 4;
q 4 — заменяем “ b ” на “ a ” и переходим в q 1 (цепочку вида заменяем на цепочку вида .
Задача 7
состояние q 1 — поиск правой (младшей) цифры числа;
состояние q 2—умножение очередной цифры числа на 2 без прибавления 1 переноса;
состояние q 3— умножение очередной цифры числа на 2 с прибавлением 1 переноса.
Задача 8
Машина Тьюринга для этой программы выглядит тривиально просто — в ней всего одно состояние. Такая машина Тьюринга выполняет следующие действия: стирает самый правый штрих, ищет разделитель (пустую ячейку) и в эту пустую ячейку помещает штрих, тем самым сформирована непрерывная последовательность штрихов длины n + m.
Однако, как ни странно, решение этой задачи вызывает большие трудности. Очень часто ученики строят машину Тьюринга, которая выполняет циклические действия: последовательно пододвигают правые n штрихов к левым.
В этом случае их программа выглядит следующим образом:
состояние q 1 —поиск разделителя;
состояние q 2—передвинули штрих;
состояние q 3—проверка на конец (все ли штрихи передвинули).
На примере этой задачи четко видно, как часто дети пытаются решить задачу уже знакомыми способами. Мне кажется, что, предлагая ученикам задачи на составление машин Тьюринга, мы развиваем способность к нахождению необычных решений, развиваем способность творчески думать!
Задача 9
Эта задача кажется школьникам достаточно легкой, но трудности возникают с остановом машины Тьюринга. Ниже приведен один из возможных вариантов машины Тьюринга для этой задачи.
Идея решения (условие останова). На ленте есть два исходных массива штрихов.
Штрихи начинаем стирать с левого конца массива m. И поочередно стираем самый левый штрих в массиве m и самый правый штрих в массиве n. Но прежде чем стереть правый штрих в массиве n, проверяем, единственный он (т.е. последний, который надо стереть) или нет.
Опишем сначала состояния машины Тьюринга, которые необходимы для решения нашей задачи, а затем составим программу-таблицу.
Состояние q 1 — поиск разделителя между массивами штрихов при движении справа налево;
состояние q 2 — поиск левого штриха в массиве m;
состояние q 3 — удаление левого штриха в массиве m;
состояние q 4 — поиск разделителя при движении слева направо;
состояние q 5 — поиск правого штриха в массиве n;
состояние q 6 — проверка единственности этого штриха в массиве n, т.е. определяем, был ли он последним;
состояние q 7 — если он был последним, то останов, иначе переход на новый цикл выполнения алгоритма.
Задача 10
При решении этой задачи следует обратить внимание на правильное выписывание алфавита:
A = < a 0, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, Д, А, Н, Е, Т>.
Состояние q 1—поиск правого конца числа;
состояние q 2—анализ младшей цифры числа; если она равна “0” или “5”, т.е. число делится на 5, то переход в состояние q 3, иначе переход в состояние q 5;
состояние q 3—запись буквы “Д” справа от слова на ленте;
состояние q 4—запись буквы “А” справа от слова и останов машины;
состояние q 5—запись буквы “Н” справа от слова;
состояние q 6—запись буквы “Е” справа от слова;
состояние q 7—запись буквы “Т” справа от слова и останов машины.
Источник: mydocx.ru
13.3. Правила функционирования машины Тьюринга
Работа машины представляет собой некоторую последовательность шагов. Шаг заключается в следующем. Головка считывает букву, записанную в ячейке, над которой она находится. В зависимости от своего состояния, представленного буквой алфавита состояний УУ, и прочтенной буквы она переходит в новое состояние (возможно подтверждение старого) и реализует команду.
В команде указано, какую букву записать и какие перемещения совершать. После выполнения команды машина готова к реализации следующего шага.
Принимая во внимание определение процесса путем задания его множества состояний (с выделением из него некоторого начального) и правил перехода из одного состояния в другое, нетрудно конкретизировать развивающийся в машине Тьюринга процесс следующим образом. Множество состояний процесса – это множество состояний УУ; в результате воздействия на процесс со стороны ленты, точнее буквы в конкретной ячейке ленты, процесс изменяет (либо сохраняет) свое состояние и откликается на внешнее воздействие записью в ячейку ленты конкретной буквы алфавита машины A. Благодаря таким действиям процесс переводит одно слово, присутствующее на ленте, в другое, причем слова представлены в одном и том же алфавите A.
Конкретная машина Тьюринга задается перечислением элементов множеств A и Q и набором правил, по которым работает машина. Они имеют вид: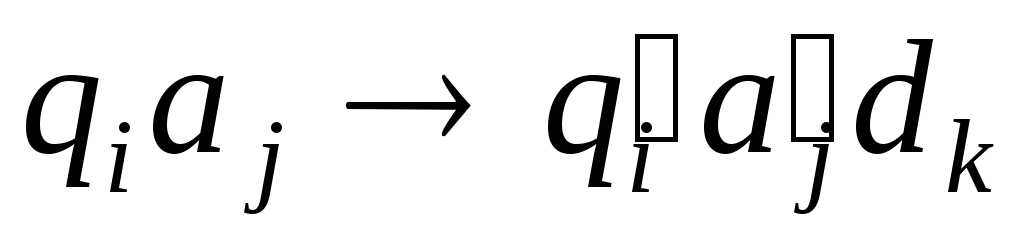 
, в ячейку вместоaj записывается 
, головка делает движениеdk, которое имеет три варианта: на ячейку влево, на ячейку вправо, остаться на месте). Для каждой возможной конфигурации qi, aj> имеется ровно одно правило. Правил нет только для заключительного состояния, попав в которое машина останавливается * . Поскольку различных множеств A и Q и правил может быть сколь угодно много, то и конкретных машин Тьюринга тоже бесконечно много.
Программой машины Тьюринга называется конечный непустой список команд (правил) машины Тьюринга, занумерованный последовательно числами 1, 2, 3, …, M. Естественно также потребовать, чтобы значения всех операндов в командах программы не выходили за пределы диапазона номеров, использованных для нумерации команд в этой программе.
Отметим также, что для представления слов, с которыми работает машина, можно без каких-либо ограничений общности рассматривать алфавит , содержащий лишь две буквы. Действительно, все, что можно записать в бесконечном алфавите 1, 2, …, можно воспроизвести и в алфавите : для этого достаточно закодировать буквы 1, 2, … словами вида , , … .
Если теперь, задавшись программой и какой-либо начальной конфигурацией (т.е. положением головки и словом на ленте), пустить машину в ход, то осуществится один из следующих трех вариантов:
- Произойдет рабочий шаг машины.
- Произойдет результативная остановка при выполнении команды СТОП. Соответствующая конфигурация машины представляет результат выполнения программы.
- Машина “зациклится”, т.е. работа машины продолжается бесконечно.
Источник: studfile.net
Программирование машины тьюринга
Машина Тьюринга — это строгое математическое построение, математический аппарат (аналогичный, например, аппарату дифференциальных уравнений), созданный для решения определенных задач. Этот математический аппарат был назван “машиной” по той причине, что по описанию его составляющих частей и функционированию он похож на вычислительную машину. Принципиальное отличие машины Тьюринга от вычислительных машин состоит в том, что ее запоминающее устройство представляет собой бесконечную ленту: у реальных вычислительных машин запоминающее устройство может быть как угодно большим, но обязательно конечным. Машину Тьюринга нельзя реализовать именно из-за бесконечности ее ленты. В этом смысле она мощнее любой вычислительной машины.
В каждой машине Тьюринга есть две части:
1) неограниченная в обе стороны лента, разделенная на ячейки;
2) автомат (головка для считывания/записи, управляемая программой).
С каждой машиной Тьюринга связаны два конечных алфавита: алфавит входных символов A = и алфавит состояний Q = . (С разными машинами Тьюринга могут быть связаны разные алфавиты A и Q.) Состояние q0называется пассивным. Считается, что если машина попала в это состояние, то она закончила свою работу. Состояние q1 называется начальным. Находясь в этом состоянии, машина начинает свою работу.
Входное слово размещается на ленте по одной букве в расположенных подряд ячейках. Слева и справа от входного слова находятся только пустые ячейки (в алфавит А всегда входит пустая буква а0 — признак того, что ячейка пуста).
Автомат может двигаться вдоль ленты влево или вправо, читать содержимое ячеек и записывать в ячейки буквы. Ниже схематично нарисована машина Тьюринга, автомат которой обозревает первую ячейку с данными.
Автомат каждый раз “видит” только одну ячейку. В зависимости от того, какую буквуai он видит, а также в зависимости от своего состояния qj автомат может выполнять следующие действия:
- · записать новую букву в обозреваемую ячейку;
- · выполнить сдвиг по ленте на одну ячейку вправо/влево или остаться неподвижным;
- · перейти в новое состояние.
То есть у машины Тьюринга есть три вида операций. Каждый раз для очередной пары (qj, ai) машина Тьюринга выполняет команду, состоящую из трех операций с определенными параметрами.
Программа для машины Тьюринга представляет собой таблицу, в каждой клетке которой записана команда.
Клетка (qj, ai) определяется двумя параметрами — символом алфавита и состоянием машины. Команда представляет собой указание: куда передвинуть головку чтения/записи, какой символ записать в текущую ячейку, в какое состояние перейти машине. Для обозначения направления движения автомата используем одну из трех букв: “Л” (влево), “П” (вправо) или “Н” (неподвижен).
После выполнения автоматом очередной команды он переходит в состояние qm(которое может в частном случае совпадать с прежним состоянием qj). Следующую команду нужно искать в m-й строке таблицы на пересечении со столбцом al (букву alавтомат видит после сдвига).
Договоримся, что когда лента содержит входное слово, то автомат находится против какой-то ячейки в состоянии q1. В процессе работы автомат будет перескакивать из одной клетки программы (таблицы) в другую, пока не дойдет до клетки, в которой записано, что автомат должен перейти в состояние q0. Эти клетки называются клетками останова. Дойдя до любой такой клетки, машина Тьюринга останавливается.
Несмотря на свое простое устройство, машина Тьюринга может выполнять все возможные преобразования слов, реализуя тем самым все возможные алгоритмы.
Машина Поста (МП) — абстрактная вычислительная машина, предложенная Эмилем Леоном Постом, которая отличается от машины Тьюринга большей простотой. Обе машины «эквивалентны» и были созданы для уточнения понятия «алгоритм».
Машина Поста состоит из каретки (или считывающей и записывающей головки) и разбитой на секции бесконечной в обе стороны ленты (см. пример ниже). Каждая секция ленты может быть либо пустой — 0, либо помеченной меткой 1. За один шаг каретка может сдвинуться на одну позицию влево или вправо, считать, поставить или стереть символ в том месте, где она стоит. Работа машины Поста определяется программой, состоящей из конечного числа строк. Для работы машины нужно задать программу и ее начальное состояние (т. е. состояние ленты и позицию каретки). Кареткой управляет программа, состоящая из строк команд. Каждая команда имеет следующий синтаксис:
где i — номер команды, K – действие каретки, j — номер следующей команды (отсылка).
Всего для машины Поста существует шесть типов команд:
1) V j — поставить метку, перейти к j-й строке программы.
2) X j — стереть метку, перейти к j-й строке программы.
a. j — сдвинуться вправо, перейти к j-й строке программы.
4) ? j1; j2 — если в ячейке нет метки, то перейти к j1-й строке программы, иначе перейти к j2-й строке программы.
5) ! – конец программы (стоп).
У команды «стоп» отсылки нет. После запуска возможны варианты:
— работа может закончиться невыполнимой командой (стирание несуществующей метки или запись в помеченное поле);
— работа может закончиться командой Stop;
— работа никогда не закончится.
Статьи к прочтению:
- Программирование обработки по дуге окружности
- Программирование операторов ассемблера
09 — Введение в алгоритмы. Машина Тьюринга
Похожие статьи:
- Модели вычислений: машина тьюринга, расп, рам, неветвящиеся программы, деревья решений Тренажёр «Машина Тьюринга» — это учебная модель универсального исполнителя (абстрактной вычислительной машины), предложенного в 1936 году А. Тьюрингом…
- Понятие машины тьюринга. формальные грамматики. Машина Тьюринга – математическая, воображаемая машина, а не машина физическая. Была предложена Аланом Тьюрингом в 1936 году для формализации понятия…
Источник: csaa.ru