Потоковый граф программы пример

Тест белого ящика — это метод разработки тестовых примеров, который использует структуру управления процедурным дизайном для получения тестовых примеров.
Тесты белого ящика проверяют, что:

• Все независимые пути каждого модуля выполняются хотя бы один раз.
• Решения используются в их истинной части и в их ложной части.
• Все циклы выполняются на пределе своих возможностей.
• Используются все внутренние структуры данных.

Базовый путь тестирование

Метод базового пути (предложенный МакКейбом) позволяет получить меру сложности процедурного дизайна и использовать эту меру в качестве руководства для определения серии базовых путей выполнения, разрабатывая тестовые примеры, которые гарантируют, что каждый путь запускается хотя бы один раз.

Обозначение потокового графа или графа программы

Представляет логический поток управления в следующих обозначениях:

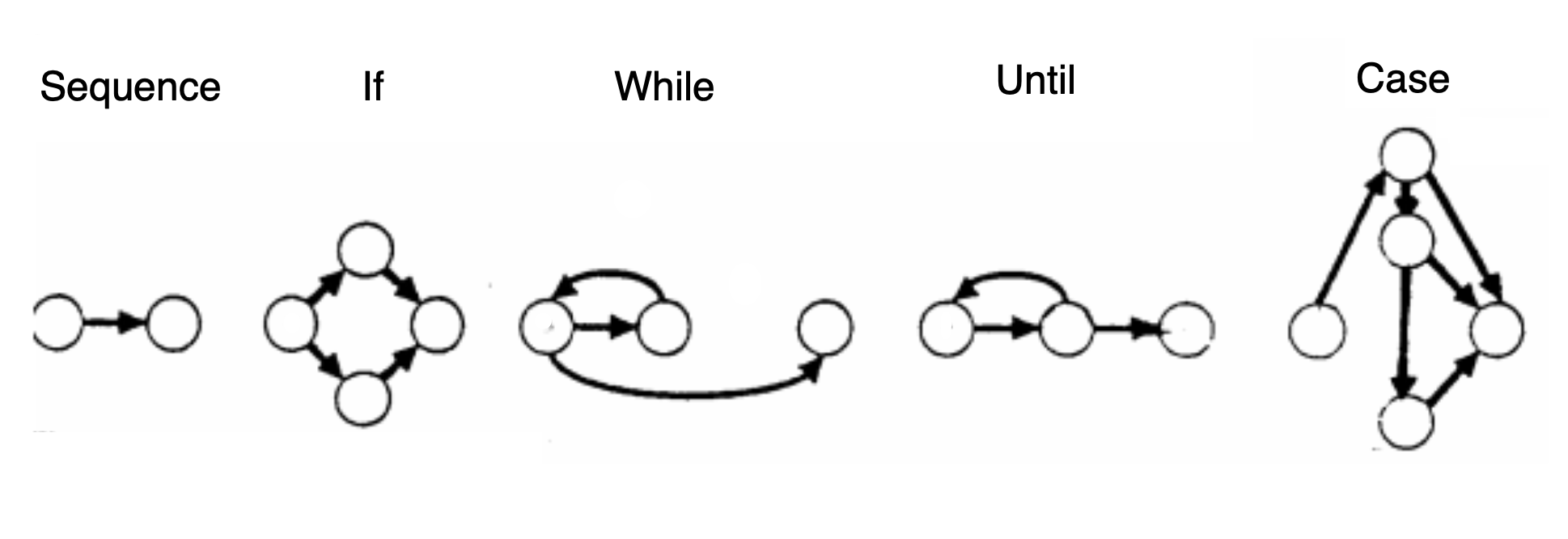
Потоковый ввод вывод в файл c++. Перегрузка операторов. Изучение С++ для начинающих. Урок #119

Вот пример, основанный на блок-схеме, представляющей управляющую структуру программы.

Цикломатическая сложность

Это мера, которая дает представление о логической сложности программы.

• Цикломатическая сложность совпадает с количеством областей потокового графа.
• Цикломатическая сложность V (G) потокового графа G определяется как V (G) = Ребра — Узлы + 2.
• Цикломатическая сложность V (G) потокового графа G также определяется как V (G) = узлы предиката + 1.

Исходя из потокового графа рисунка, цикломатическая сложность будет следующей:

• Поскольку на графике четыре области, V (G) = 4
• Поскольку в графе 11 ребер и 9 узлов, V (G) = 11 — 9 — 2 = 4.
• Поскольку в графе 3 узла предиката, V (G) = 3 + 1 = 4

Из значения цикломатической сложности мы получаем количество независимых путей, что дает нам предельное значение для количества тестов, которые мы должны разработать.
В этом примере количество независимых дорог равно 4, а независимых дорог находятся:

• 1–11
• 1–2–3–4–5–10–1–11
• 1–2–3–6–7–9–10–1–11
• 1–2–3–6–8–9–10–1–11

Этапы разработки теста по основному пути

• Получите блок-схему из кода проекта или модуля.
• Получите цикломатическую сложность потокового графа.
• Определите базовый набор независимых путей.
• Определите тестовые примеры, которые разрешают выполнение каждого из предыдущих путей.
• Выполните каждый тестовый пример и убедитесь, что результаты соответствуют ожидаемым.

Циклическое тестирование

Циклы являются краеугольным камнем подавляющего большинства алгоритмов, реализованных в программном обеспечении, поэтому мы должны уделять особое внимание при тестировании программного обеспечения.

Графы, вершины, ребра, инцидентность, смежность

Циклический тест — это метод тестирования белого ящика, который фокусируется на валидности построений цикла.

Можно определить четыре различных типа петель:

• Простые петли.
• Вложенные петли.
• Составные петли.
• Неструктурированные петли.

Простые петли

Следующий набор тестов необходимо применить к простым циклам (из n итераций):

• Пропустить петлю.
• Пропустить только один раз через петлю.
• Пройдите петлю дважды.
• Сделайте m шагов петли с помощью m ‹n
• Выполните n — 1, n и n + 1 шагов по циклу.

Вложенные циклы

Если мы расширим набор тестов с простых циклов до вложенных циклов, количество тестов вырастет геометрически, поэтому Бейзер предлагает следующий набор тестов для вложенных циклов:

• Начните с самого внутреннего цикла, установив для остальных циклов минимальные значения.
• Выполните простые тесты цикла для самого внутреннего цикла, сохраняя значения итераций самых внешних циклов на минимальных значениях.
• Переходите к следующему самому внешнему циклу, сохраняя минимальные значения самых внешних циклов.
• Продолжайте, пока все петли не будут проверены.

Составные циклы

Проверьте составные циклы, используя методы тестирования простых циклов, рассматривая их как независимые циклы.

Неструктурированные петли

Измените дизайн этих циклов, чтобы они соответствовали конструкциям структурного программирования.

Применяя теорию

Потоковый граф

Для представления программы используется потоковый граф. Перечислим его особенности.

1. Граф строится отображением управляющей структуры программы. В ходе отображения закрывающие скобки условных операторов и операторов циклов (end if; end loop) рассматриваются как отдельные (фиктивные) операторы.

2. Узлы (вершины) потокового графа соответствуют линейным участкам программы, включают один или несколько операторов программы.

3. Дуги потокового графа отображают поток управления в программе (передачи управления между операторами). Дуга — это ориентированное ребро.

4. Различают операторные и предикатные узлы. Из операторного узла выходит одна дуга, а из предикатного — две дуги.

4. Предикатные узлы соответствуют простым условиям в программе. Составное условие программы отображается в несколько предикатных узлов. Составным называют условие, в котором используется одна или несколько булевых операций (OR, AND).

5. Например, фрагмент программы

вместо прямого отображения в потоковый граф вида, показанного на рис. 6.4, отображается в преобразованный потоковый граф (рис. 6.5).

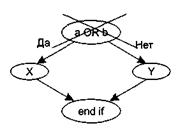
Рис. 6.4. Прямое отображение в потоковый граф

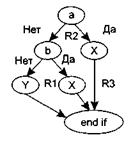
Рис. 6.5. Преобразованный потоковый граф

6. Замкнутые области, образованные дугами и узлами, называют регионами.

7. Окружающая граф среда рассматривается как дополнительный регион. Например, показанный здесь граф имеет три региона — Rl, R2, R3.

Пример 1. Рассмотрим процедуру сжатия:

1 выполнять пока нет EOF

1 читать запись;

2 если запись пуста

3 то удалить запись:

4 иначе если поле а >= поля b

6иначе удалить а;

7b конец выполнять;

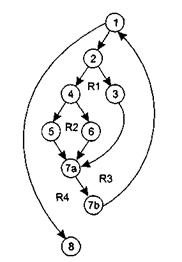
Рис. 6.6. Преобразованный потоковый граф процедуры сжатия

Она отображается в потоковый граф, представленный на рис. 6.6. Видим, что этот потоковый граф имеет четыре региона.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник: studopedia.ru

9. Потоковый граф и цикломатическая сложность программы. Примеры.

Для представления программы используется потоковый граф. Перечислим его особенности.

Граф строится отображением управляющей структуры программы. В ходе отображения закрывающие скобки условных операторов и операторов циклов (end if; end loop) рассматриваются как отдельные (фиктивные) операторы.

Узлы (вершины) потокового графа соответствуют линейным участкам программы, включают один или несколько операторов программы.

Дуги потокового графа отображают поток управления в программе (передачи управления между операторами). Дуга — это ориентированное ребро.

Различают операторные и предикатные узлы. Из операторного узла выходит одна дуга, а из предикатного — две дуги.

5. Предикатные узлы соответствуют простым условиям в программе. Составное условие программы отображается в несколько предикатных узлов. Составным называют условие, в котором используется одна или несколько булевых опера­ций (OR, AND).

Например, фрагмент программы

вместо прямого отображения в потоковый граф вида, показанного на рис. 5.3, отображается в преобразованный потоковый граф (рис. 5.4).

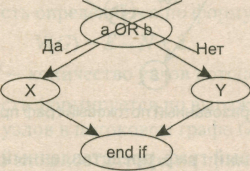
Рис. 5.3. Прямое отображение в потоковый граф

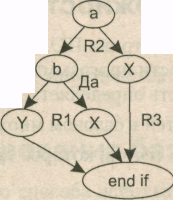
Рис. 5.4. Преобразованный потоковый граф

Замкнутые области, образованные дугами и узлами, называют регионами.

Окружающая граф среда рассматривается как дополнительный регион. Например, показанный здесь граф имеет три региона — Rl, R2, R3.

Цикломатическая сложность — метрика ПО, которая обеспечивает количествен­ную оценку логической сложности программы. В способе тестирования базового пути цикломатическая сложность определяет:

количество независимых путей в базовом множестве программы;

верхнюю оценку количества тестов, которое гарантирует однократное выполнение всех операторов.

Независимым называется любой путь, который вводит новый оператор обработки или новое условие. В терминах потокового графа независимый путь должен со­держать дугу, не входящую в ранее определенные пути.

Путь начинается в начальном узле, а заканчивается в конечном узле графа. Независи­мые пути формируются в порядке от самого короткого к самому длинному. Каждый новый путь включает новую дугу.

Все независимые пути графа образуют базовое множество.

Свойства базового множества:

1) тесты, обеспечивающие его проверку, гарантируют:

— однократное выполнение каждого оператора;

— выполнение каждого условия по True-ветви и по False-ветви;

2) мощность базового множества равна цикломатической сложности потокового графа.

Мощность базового множества дает априорную оценку коли­чества независимых путей, которое имеет смысл искать в графе.

Цикломатическая сложность вычисляется одним из трех способов:

цикломатическая сложность равна количеству регионов потокового графа;

цикломатическая сложность определяется по формуле: V(G)=E-N+2, где Е — количество дуг, N — количество узлов потокового графа;

цикломатическая сложность формируется по выражению V(G) = р + 1, где р — количество предикатных узлов в потоковом графе G.

Вычислим цикломатическую сложность графа из примера каждым из трех спо­собов:

потоковый граф имеет 3 региона;

V(G) = 7 дуг — 6 узлов + 2 = 3;

V(G) = 2 предикатных узла +1= 3.

Источник: studfile.net