Для построения графика функции одной переменной, прежде всего, необходимо задать множество (диапазон) значений независимой переменной и соответствующее множество значений зависимой (функциональной) переменной. После этого следует воспользоваться мастером построения диаграмм программы MS Excel для изображения графика заданной функциональной зависимости. При этом задание значений независимой переменной удобно выполнить с помощью рассмотренной ранее операции автозаполнения. Ниже приводится описание последовательности практических действий для примера построения графика функции: f(x) = 2x 2 — Зx — 5 в интервале изменения независимой переменной: х∈[-5, 5] .
Для начала рекомендуется создать новую книгу с именем Графики Функций. На отдельном листе в ячейку А1 введем текст «Значения переменной:», а в ячейку В1 введем текст «Значения функции:». Хотя исходная независимая переменная принимает значения из непрерывного интервала действительных чисел [-5, 5], для построения графика необходимо для этой независимой переменной задать дискретные значения. Для наших целей вполне достаточно рассмотреть последовательный диапазон значений от -5 до 5 с интервалом их изменения, равным 0,1.
Алгебра 7 класс. 3 октября. Строим график линейной функции
Для задания этого диапазона значений в ячейку А2 введем наименьшее значение интервала изменения независимой переменной: число -5, а в ячейку А3 — число -4,9. После чего вторым способом автозаполнения запишем диапазон значений независимой переменной в ячейки А2:А102. Далее в ячейку В2 введем формулу: =2*A2^2-3*A2-5 , которую с помощью первого способа автозаполнения запишем в ячейки В2:В102. Результат выполнения данной последовательности операций по подготовке исходных данных будет иметь следующий вид (рис. 1).
Рис. 1. Исходные данные для построения графика функции одной переменной
Для построения графика необходимо воспользоваться мастером диаграмм, который может быть вызван с помощью кнопки стандартной панели инструментов или операции главного меню: Вставка → Диаграмма (рис. 2). Мастер диаграмм представляет собой самостоятельное диалоговое окно с набором вкладок, обеспечивающих задание отдельных свойств элементам графического изображения.
Рис. 2. Внешний вид диалогового окна мастера диаграмм (шаг 1 из 4)
На первой из вкладок содержится список стандартных диаграмм, которые могут быть использованы дня графического представления рядов данных. На второй вкладке пользователю предлагается выбор диаграммы из списка нестандартных, часть которых появилась в последних версиях программы MS Excel.
На первом шаге построения диаграммы необходимо выбрать тип диаграммы и ее вид. С этой целью следует выделить на вкладке Все диаграммы в левом списке тип диаграммы График, а в правом списке с графическими миниатюрами — первый вид графика, который отражает развитие процесса во времени или по категориям. После выбора типа и разновидности диаграммы следует нажать кнопку Далее и перейти ко второму шагу построения диаграммы с помощью мастера диаграмм (рис. 3).
Построить график ЛИНЕЙНОЙ функции и найти:
Рис. 3. Спецификация источника данных для построения графика с помощью мастера диаграмм (шаг 2 из 4)
Первая из вкладок (рис. 3, а) служит для задания диапазона значений рядов данных, которые будут отображены на диаграмме. С этой целью на втором шаге построения диаграммы необходимо выбрать ячейки с данными, которые должны быть отображены на соответствующем графике. Применительно к рассматриваемому примеру это значения функции, которые содержатся в диапазоне ячеек В2:В102.
Для указания этих значений следует установить переключатель Строка / столбец так, чтобы в левом окне были Элементы легенды (ряды). После этого выполнить щелчок на строке «Значения функции:», и затем на расположенной выше кнопке Изменить или Добавить.
В результате будет открыто дополнительное небольшое окно, в строке Значения необходимо указать источник данных диаграммы. Для указания источника данных следует на рабочем листе «Квадратный трехчлен» с помощью мыши или клавиатуры выделить диапазон значений функции В2:В102.
Он будет иметь специальную рамку в форме мерцающей пунктирной линии, а в соответствующей строке появится надпись с указанием имени рабочего листа и абсолютных адресов ячеек этого диапазона (рис. 3, б). Далее на этом же шаге работы мастера диаграмм следует задать подписи по горизонтальной оси. С этой целью необходимо перейти на строку «Значения функции:» и выполнить щелчок на кнопке с именем Изменить и выбрать строку Имя ряда. Оба шага можно выполнить одновременно.
Рис. 4. Спецификация подписи горизонтальной оси X для построения графика с помощью мастера диаграмм (шаг 2 из 4)
В результате будет открыто дополнительное небольшое окно, в единственной строке которого необходимо указать источник данных для независимой переменной графика. Для указания соответствующего источника данных следует на рабочем листе «Квадратный трехчлен» с помощью мыши или клавиатуры выделить диапазон значений функции А2:А102.
Выделенный диапазон также приобретет специальную рамку в форме мерцающей пунктирной линии, а в соответствующей строке появится надпись с указанием имени рабочего листа и абсолютных адресов ячеек этого диапазона (рис. 4, б). После выбора спецификации рядов данных и подписей оси X для графика следует перейти к третьему шагу построения диаграммы с помощью мастера диаграмм (рис. 5).
Рис. 5. Спецификация названия диаграммы и выбор варианта ее размещения с помощью мастера диаграмм (шаги 3 и 4 из 4)
На третьем шаге на вкладке Работа с диаграммами можно задать заголовки и названия диаграммы и осей, подписи данных и линии сетки. Применительно к рассматриваемому примеру можно указать название графика в соответствующем поле ввода. После спецификации параметров диаграммы следует сохранить изменения и перейти к последнему четвертому шагу построения диаграммы с помощью мастера диаграмм (рис. 5).
На этом шаге следует выбрать один из двух вариантов размещения диаграммы: на отдельном рабочем листе или на текущем рабочем листе, где содержатся ячейки с данными диаграммы. При необходимости можно изменить имя диаграммы, предлагаемой мастером по умолчанию. После этого следует нажать кнопку Готово. В результате будет построена диаграмма в форме графика кривой квадратного трехчлена (рис. 6).
![Рис. 6. Результат построения графика функции: f(x) = 2x² - Зx - 5 в интервале изменения независимой переменной: х∈[-5, 5]](https://img-fotki.yandex.ru/get/194778/40446132.f7/0_cd323_a555bcec_orig.jpg)
Рис. 6. Результат построения графика функции: f(x) = 2x² — Зx — 5 в интервале изменения независимой переменной: х∈[-5, 5]
После построения диаграммы в случае необходимости можно редактировать отдельные ее свойства. Доступ к редактированию свойств построенной диаграммы можно получить либо с помощью контекстного меню диаграммы, либо с помощью операций меню Работа с диаграммами. Удобным оказывается способ получения доступа к выделенным элементам диаграммы с помощью комбинации клавиш: Ctrl+1 или двойного щелчка левой кнопкой мыши.
Так, например, для изменения цвета фона построенного графика квадратного трехчлена можно выполнить двойной щелчок левой кнопкой мыши на фоне соответствующего рисунка. В появившемся диалоговом окне выбрать желаемый цвет фона графика из предлагаемой палитры цветов. Аналогично можно изменить цвет линии кривой графика и интервал отображения промежуточных значений независимой и зависимой переменных. Изображенный на рис. 6 график функции получен после редактирования его свойств в результате изменения цвета фона диаграммы, линии кривой графика и интервала отображения промежуточных значений независимой переменной.
Источник: excelexpert.ru
4.8.4. Вычисление функций и построение графиков
Excel предоставляет широкие возможности как для выполнения вычислений различных уравнений и функций, так и для наглядного отображения полученных результатов в виде двух- и трехмерных графических изображений. Графики позволяют пользователю не только получить наглядное отображение, но и в ряде случаев получить приближенное графическое решение задачи. Решение задачи построения графика в Excel состоит из двух основных этапов:
- формирования данных и результата решения задачи в ячейках Excel для построения графика на плоскости;
- построения и оформление графика и другого графического объекта, например поверхностей в пространстве.
Вычисление функций одной переменной
Рассмотрим построение функции у=2х+1, представляющей собой уравнение линии для значений х= (0; +10) с шагом ∆х=1. Задача построения прямой, как и любой диаграммы в Excel разбивается на несколько этапов в соответствии. Этап 1. Ввод данных. Прежде, чем построить прямую, необходимо составить таблицу данных x и y в рабочем окне таблицы Excel.
Для этого значения x и y следует представить в виде таблицы, где столбцами являются соответствующие показатели. Пусть в рассматриваемом примере столбец А будет использоваться для аргументов x, а столбец В – для значений функции прямой y.
Для введения значений аргумента х в ячейку А2 вводится первое значение аргумента (0), а в ячейку A3 — второе значение аргумента с учетом заданного шага (1). Выделив блок ячеек А2:АЗ, и, используя режим автозаполнения, формируем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А12).
Затем в ячейку В2 вводим ее уравнение: =2*A2+1, а затем копируем эту формулу в диапазон В2:В12. В результате должна быть получена следующая таблица исходных данных (Рис.4.38.). Этап 2. Построение графика прямой.
После запуска программы Мастер диаграмм в появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы выбираем тип диаграммы — График, а вид — График с маркерами и нажимаем кнопку Далее в диалоговом окне. Этап 3. Указание диапазона.
В появившемся диалоговом окне Мастер диаграмм (шаг 2 из 4): источник данных диаграммы необходимо выбрать вкладку Диапазон данных и в поле Диапазон указать интервал данных, то есть ввести ссылку на ячейки, содержащие данные, которые необходимо представить на диаграмме.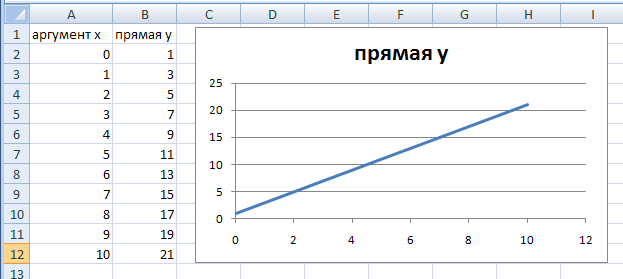 
Вычисление и построение функции у=2х+1 Определение диапазона данных является ответственным моментом построения диаграммы, необходимо указать только те данные, которые должны быть изображены на диаграмме. Кроме того, для введения поясняющих надписей (легенды), они также должны быть включены в диапазон (в примере – прямая у).
Этап 4. Ввод надписей по оси X (горизонтальной) и У (вертикальной). В диалоговом окне Мастер диаграмм (шаг 2 из 4): источник данных диаграммы необходимо выбрать вкладку Ряд (щелкнув на ней указателем мыши) и в поле Подписи оси X указать диапазон подписей (в примере — аргумент х).
Для этого следует активизировать поле Подписи оси х, щелкнув в нем указателем мыши, и, наведя его на левую верхнюю ячейку подписей (А2), нажать левую кнопку мыши, затем, не отпуская ее, протянуть указатель мыши к правой нижней ячейке, содержащей выносимые на ось X подписи (А12), затем отпустить левую кнопку мыши. После появления требуемой записи диапазона необходимо нажать кнопку Далее.
Этап 5. Введение заголовков. В третьем окне Мастер диаграмм (шаг 3 из 4): параметры диаграммы требуется ввести заголовок диаграммы и названия осей. Для этого необходимо выбрать вкладку Заголовки, щелкнув на ней указателем мыши. Щелкнув в рабочем поле Название диаграммы указателем мыши, ввести с клавиатуры в поле название: Прямая.
Затем аналогичным образом ввести в рабочие поля Ось X (категорий) и Ось Y (значений) соответствующие названия: Аргумент и Значения. Далее в данном окне необходимо выбрать вкладку Легенда и указать ее необходимость для обозначения функций, для чего устанавливаем флажок в поле Добавить легенду и нажимаем кнопку Далее.
Этап 6. Выбор места размещения. В четвертом окне Мастер диаграмм (шаг 4 из 4): размещение диаграммы необходимо указать место размещения диаграммы. Для этого переключатель Поместить диаграмму на листе необходимо установить в нужное положение: на отдельном или текущем листе.
Если диаграмма имеет желаемый вид, необходимо нажать кнопку Готово, иначе следует нажать кнопку Назад и изменить установки. В качестве второго примера рассмотрим построение функции одной переменной у=f(x) на примере уравнения параболы y=x 2 для значений х=(-5; +5) с шагом ∆х=0.5.
Задача построения параболы во многом аналогична построению прямой, поэтому рассмотрим основные этапы без излишней детализации. Этап 1. Ввод данных и вычисление функции. Для построения параболы необходимо составить таблицу данных (х и у).
В рассматриваемом примере столбец А будет использоваться для значений аргумента х, а столбец В – для значений функции у. В ячейку А1 вводим Аргумент, а в ячейку В1 — Парабола. Далее в ячейку А2 вводим первое значение аргумента (-5), в ячейку A3 вводится второе значение аргумента (–4,5) и затем, выделив блок ячеек А2:АЗ, автозаполнением вводим все значения аргумента.
Далее в ячейку В2 вводим уравнение параболы: =А2*А2 и копируем эту формулу в диапазон ячеек В2:В14. В результате должна быть получена следующая таблица исходных данных (рис.4.39).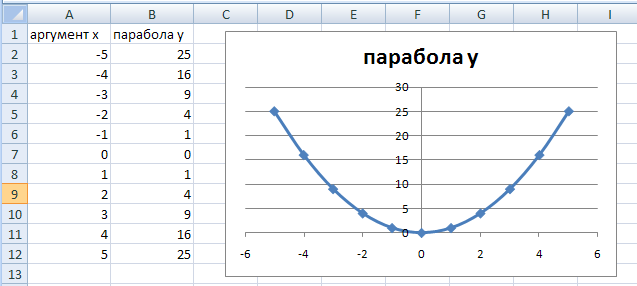 
Рис.4.39. Вычисление и построение параболы y=x 2 Этап 2. Выбор типа диаграммы.
На панели инструментов Стандартная необходимо нажать кнопку Мастер диаграмм. В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы указать тип диаграммы. В рассматриваемом примере выберем тип — График, вид — График с маркерами (левую среднюю диаграмму в правом окне). После чего нажимаем кнопку Далее в диалоговом окне.
Этап 3. Указание диапазона. В появившемся диалоговом окне Мастер диаграмм (шаг 2 из 4): источник данных диаграммы необходимо выбрать вкладку Диапазон данных и в поле Диапазон указать интервал данных, то есть ввести ссылку на ячейки, содержащие данные, которые необходимо представить на диаграмме.
Для этого с помощью клавиши Delete необходимо очистить рабочее поле Диапазон и, убедившись, что в нем остался только мигающий курсор, навести указатель мыши на левую верхнюю ячейку данных (В1), нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к правой нижней ячейке, содержащей выносимые на диаграмму данные (В12), затем отпустить левую кнопку мыши. В рабочем поле должна появиться запись: =Лист1!$В$1:$В$12.
Здесь наиболее важным для нас является указание диапазона В1:В12, что подтверждает правильное введение интервала данных. Если с первого раза не удалось получить требуемую запись в поле Диапазон, действия необходимо повторить. Далее необходимо указать в строках или столбцах расположены ряды данных.
В примере значения точек параболы расположены в столбце, поэтому переключатель Ряды в с помощью указателя мыши следует установить в положение столбцах (черная точка должна стоять около слова столбцах). Этап 4. Ввод подписей по оси X (горизонтальной).
В диалоговом окне Мастер диаграмм (шаг 2 из 4): источник данных диаграммы необходимо выбрать вкладку Ряд (щелкнув на ней указателем мыши) и в поле Подписи оси X указать диапазон подписей (в примере — Аргумент). Для этого следует активизировать поле Подписи оси X, щелкнув в нем указателем мыши, и, наведя указатель мыши на левую верхнюю ячейку подписей (А2), нажать левую кнопку мыши, затем, не отпуская ее, протянуть указатель мыши к правой нижней ячейке, содержащей выносимые на ось X подписи (А12), затем отпустить левую кнопку мыши.
В рабочем поле должна появиться запись: =Лист1!$А$2:$А$14. Здесь, как и для данных, наиболее важным для нас является указание диапазона А2:А14, что подтверждает правильное введение интервала подписей. После появления требуемой записи диапазона необходимо нажать кнопку Далее. Этап 5. Введение заголовков.
В третьем окне Мастер диаграмм (шаг 3 из 4): параметры диаграммы требуется ввести заголовок диаграммы и названия осей. Для этого необходимо выбрать вкладку Заголовки, щелкнув па ней указателем мыши. Щелкнув в рабочем поле Название диаграммы указателем мыши, ввести с клавиатуры в поле название График параболы.
Затем аналогичным образом ввести в рабочие поля Ось X (категорий) и Ось Y (значений) соответствующие названия и после чего нажать кнопку Далее. Этап 6. Выбор места размещения. В четвертом окне Мастер диаграмм (шаг 4 из 4): размещение диаграммы необходимо указать место размещения диаграммы.
Для этого переключатель Поместить диаграмму на листе установить в нужное положение (на отдельном или текущем листе). В примере устанавливаем переключатель в положение имеющемся (щелчком указателя мыши черную точку устанавливаем слева от слова имеющемся). Этап 7. Завершение. Если диаграмма в демонстрационном поле имеет желаемый вид параболы, необходимо нажать кнопку Готово. В противном случае следует нажать кнопку Назад и изменить установки.
Источник: studfile.net
Построение графика функции заданной формулой программой или таблицей значений
9 февраля, 2014 
Andrey K
(31 голос, значение: 3,84 из 5)
Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.
Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
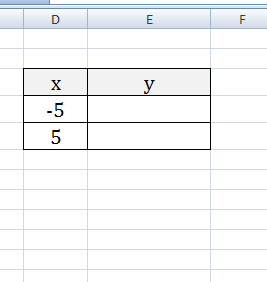
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
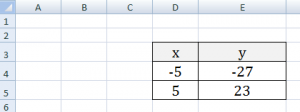
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
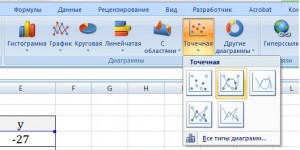
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
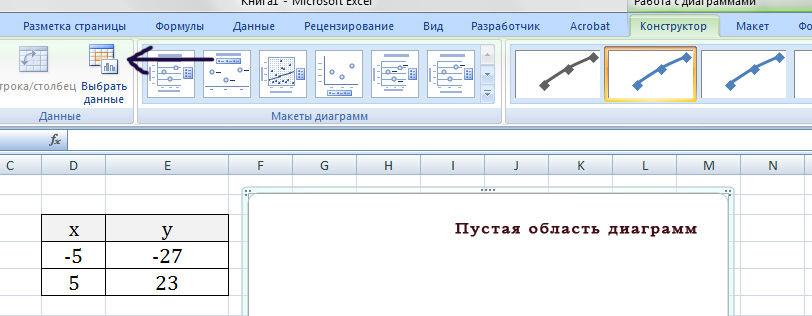
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
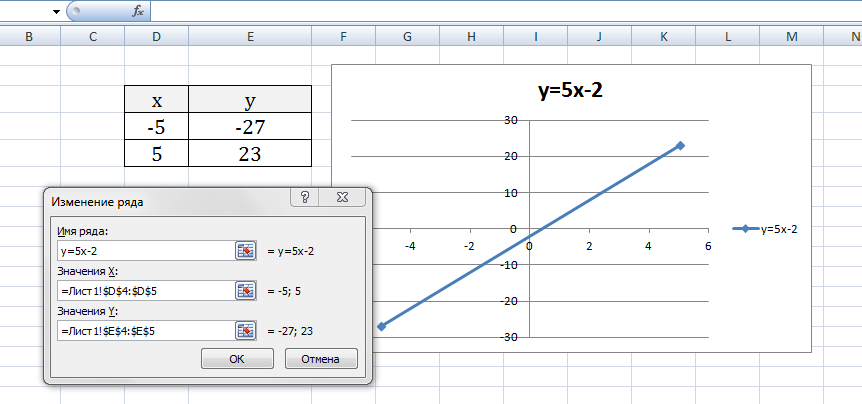
Нажимаем ОК. Перед нами график линейной функции.
2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2x 2 -2
Параболу по двум точкам уже не построить, в отличии от прямой.
Зададим интервал на оси x, на котором будет строиться наша парабола. Выберу [-5; 5].
Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу 0,2.
Заполняю столбец со значениями х, используя маркер автозаполнения до значения х=5.
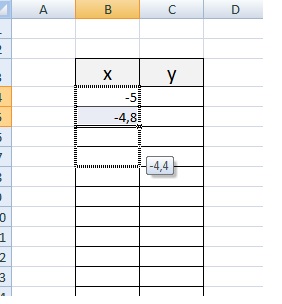
Столбец значений у рассчитывается по формуле: =2*B4^2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
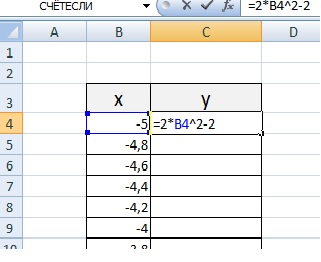
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.
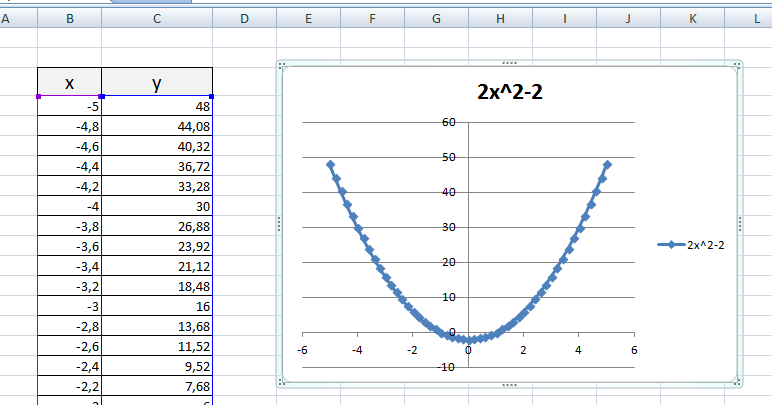
Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.
Рассмотрим это на примере функции у=1/х.
Функция определена на интервалах (- беск;0) и (0; +беск)
Создадим график функции на интервалах: [-4;0) и (0; 4].
Подготовим две таблички, где х изменяется с шагом 0,2:
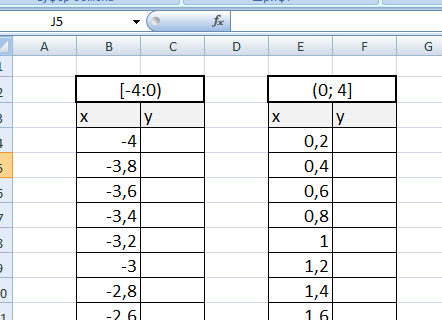
Находим значения функции от каждого аргумента х аналогично примерам выше.
На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно
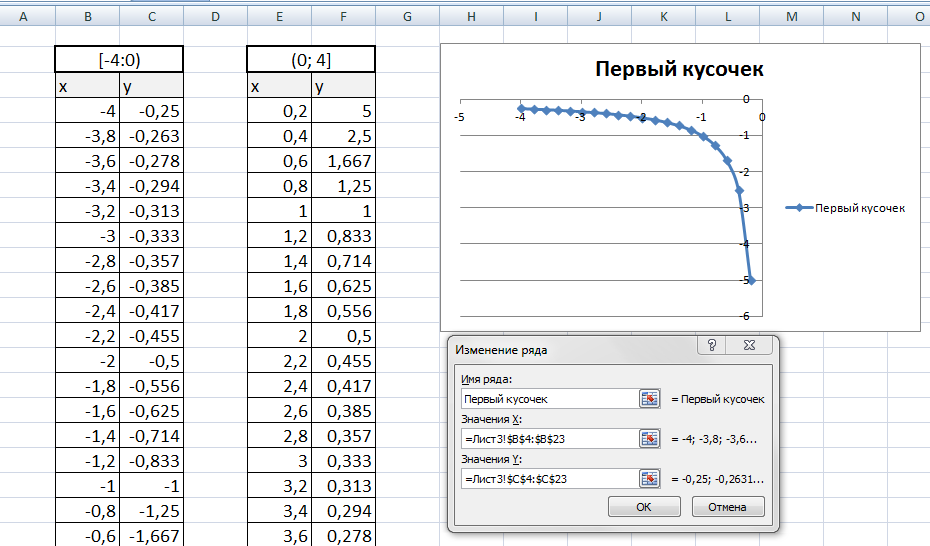
Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички
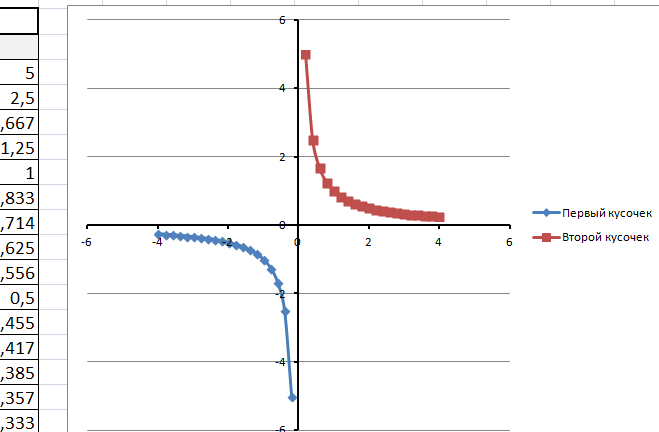
Получаем график функции y=1/x
В дополнение привожу видео — где показан порядок действий, описанный выше.
В следующей статье расскажу как создать 3-мерные графики в Excel.
Спасибо за внимание!
(31 голос, значение: 3,84 из 5)
Опубликовано в рубрике Теория и практика 
Метки: excel, графики в Excel
Вы можете оставить комментарий, или ссылку на Ваш сайт.
7 комментариев к записи “Построение графиков функций в Excel”
Пробовал зарегистрироваться, но поле с адресом эл. почты показывает, что адрес неправильный. Не знаю почему?
Вопрос к вам такой: как построить график в Excel по двум точкам?
Например,
точка А имеет координаты 3;5
точка В имеет координаты 2;7
точка С имеет координаты 4;9
точка D имеет координаты 5;8
и т.д.
Подскажите, пожалуйста.
Стоит Офис 2010
Окей, Андрей!
Действительно, получилось!
Еле нашёл тип «точечная, с отрезками». Слов нет — деревня! Это я про себя, конечно.
Андрей, спасибо большое!
PS. Только не пойму, как программа считает точки на отрезках? В какой последовательности она расставляет: ряд №…; точка»…(…)».
Никак не могу уловить закономерность.