Как вам уже известно, компьютер — это программно-управляемая система для работы с информацией, и именно программное управление делает его столь универсальным. Тому, как составляются программы, посвящена эта часть курса информатики и информационных технологий. А начнем мы ее с двух базовых понятий: «алгоритм» и «программа».
Алгоритм1 — одно из фундаментальных понятий информатики. Этим словом обозначают точное и безотказное предписание последовательности действий, переводящей автоматическое устройство из исходного состояния в результирующее. Т.е. мы можем считать алгоритмом любую инструкцию, если:
ее команды не допускают различных вариантов исполнения;
указания предусмотрены для всех возможных вариантов развития событий.
С этой точки зрения можно составить, к примеру, алгоритм переливания из пустого в порожнее. Однако, на практике алгоритмы составляют для решения тех или иных задач, т.е. получения необходимых результатов по заданным исходным данным. Вид алгоритма, да и сама возможность его написания зависят от исполнителя (это может быть и человек, и автоматическое устройство), или точнее, от его системы команд (т.е. набора инструкций, которые он «умеет» выполнять). Поэтому, в дальнейшем мы будем пользоваться следующим определением.
Теория и практика алгоритмов: понятие алгоритма
Алгоритм решения задачи — это последовательность допустимых команд исполнителя, определяющих его действия по переходу от исходных данных к искомому результату.
Какими свойствами должен обладать алгоритм? Перечислим их:
дискретность2 — алгоритм делится на отдельные элементарные шаги;
определенность — каждая команда однозначно определяет действие исполнителя;
конечность(результативность) — алгоритм должен завершаться за конечное число шагов.
Кроме этого, алгоритм может обладать еще одним полезным (но не обязательным) свойством — массовостью. Это значит, что он будет годиться не для одной конкретной задачи, а для целого класса похожих задач.
С определенностью непосредственно связана существенная особенность, о которой нельзя забывать: исполнитель выполняет алгоритм формально3, абсолютно не задумываясь над смыслом производимых действий. Поэтому не стоит обижаться на компьютер, «не догадавшийся», что вы подразумевали, — он честно делает то, что вы написали.
Существует много разных способов записи алгоритмов: графические (например, в виде блок-схем), с помощью естественного языка, какими-нибудь условными знаками идр. Но если мы хотим, чтобы алгоритм был исполнен компьютером, он должен быть обязательно записан на особом языке. Такая запись называется программой4, а язык — языком программирования.
Вы знаете, что вся информация в компьютере представляется в виде двоичных кодов. В кодах, каждый из которых обозначал одно простейшее действие (вроде, «перенести число из одной ячейки памяти в другую»), приходилось писать и программы для первых ЭВМ. Но это занятие очень сложное и кропотливое, а кроме того, требующее глубокого знания особенностей конкретной машины.
Вычислительная сложность алгоритма
Поэтому были придуманы языки программирования высокого уровня. Программа на таком языке — это последовательность команд, обозначаемых словами естественного языка или их сокращениями. Каждая из них соответствует последовательности из десятков, а то и сотен машинных команд. В результате запись получается гораздо более компактной и понятной.
Но процессор не понимает команд языков высокого уровня, поэтому их предварительно нужно «перевести». Для этого служат особые программы — трансляторы5.
Сейчас в мире существует множество языков программирования, рассчитанных на различные области применения. Мы в нашем курсе будем использовать Лого6 — язык, специально созданный для обучения основам программирования. Этот язык очень простой (кстати, в отличие от профессиональных языков программирования, он позволяет записывать команды на русском языке), но, в то же время, способствует формированию навыков, позволяющих затем, при желании, без особых проблем перейти к работе с такими популярными языками, как Си или Паскаль. Особо знаменит язык Лого своей «черепашьей графикой». О том, что это такое, мы и поговорим в следующей главе.
Algorithmi (лат.) — искаженное имя математика IX века аль-Хорезми, предложившего способ выполнения арифметических вычислений с многозначными числами.
Заметим, что подход к определению алгоритма как последовательности операций — не единственно возможный. Кроме такого — процедурного (императивного), возможен и функциональный подход, когда алгоритм рассматривается как система функций.
Discrete (англ.) — состоящий из отдельных частей
Formalis (лат.) — строго по установленным правилам
Programma (греч.) — распоряжение
Translator (англ.) — переводчик
Язык Лого (Logo, от греч. Logos — слово, мысль) разработан в 1972 г. Сеймуром Пейпертом (Массачусетский Технологический институт, США). «Прародителем» его был наиболее известный из языков функционального программирования — Лисп, однако, в процессе развития Лого приобрел ряд особенностей, позволяющих использовать при работе с ним как функциональный, так и процедурный подходы.
Источник: smekni.com
Алгоритмы и программы
Аннотация: Предмет науки программирования. Пример и свойства алгоритма. Парадигмы программирования (директивное, объектно-ориентированное и функционально-логическое программирование).
Эта глава, с которой начинается изучение курса, служит двум основным целям:
- подготовить необходимую теоретическую базу для последующего овладения различными методами обработки информации, навыками программирования в малом и построения правильных эффективных программ;
- дать минимально необходимые для практического программирования знания о языке Java и предоставить образцы небольших типовых программ.
В процессе знакомства с теоретическим материалом главы может возникнуть ощущение его оторванности от нужд практики — решения конкретных задач на языке Java. С другой стороны, именно решение задач на программирование должно привести к осознанному пониманию того факта, что написать правильную и эффективную программу совсем не так просто, как это кажется на первый взгляд.
Знание необходимых теоретических основ позволит во второй главе перейти к изучению методов построения программ и доказательства их правильности — теории, которая будет применяться для практического написания программ параллельно со знакомством с ней. Таким образом, два кажущиеся совершенно не связанными друг с другом потока изучения материала — теоретический и практический, сольются в один уже в следующей главе. Пока же читателю остается только поверить в то, что знание всего материала первой главы является необходимым условием для успешного перехода к изучению следующей.
И последнее замечание — чисто технологическое. На первой стадии изучения языка Java полезно отвлечься от того факта, что он является объектно-ориентированным, и сосредоточиться на содержательных проблемах корректной реализации алгоритма. Однако это не так просто сделать — написание даже самой простейшей программы на нем невозможно без понимания основных концепций ООП. Для частичного решения этой проблемы используется созданный специально для этих целей класс Xterm , ограждающий начинающего программиста от сложностей реального мира языка Java.
Предмет науки программирования
С давних пор человеку приходится создавать описания последовательностей действий, требуемых для достижения некоторой поставленной цели. Такие описания могут быть рассчитаны на их выполнение людьми или автоматическими устройствами. Тексты, написанные для людей, как правило, обладают известной степенью неопределенности и неформальности. Примером может служить фраза из кулинарного рецепта о щепотке соли. Только весьма опытный человек в состоянии правильно посолить блюдо в соответствии с подобной рекомендацией.
Этот пример вполне объясняет, почему описания последовательности действий, предназначенные для автоматического устройства, должны быть совершенно однозначны и заданы с помощью некоторой формальной системы обозначений. Очень часто создание таких описаний связано со значительными техническими и принципиальными трудностями. Данная проблема стала чрезвычайно актуальной в связи с повсеместным распространением электронных вычислительных машин (ЭВМ), часто используемых в качестве универсального исполнителя команд .
Описание последовательности действий, достаточно определенное для того, чтобы ее можно было выполнить при помощи некоторого автоматического устройства называют алгоритмом (algorithm) . Обычно эту последовательность записывают (кодируют) с помощью некоторых формальных обозначений. При этом формальная система, предназначенная для записи алгоритмов, называется алгоритмическим языком , сам текст алгоритма — программой , а процесс его создания — программированием .
Наука программирования (computer science) занимается исследованием свойств алгоритмов и разработкой методов построения программ. По своему положению и используемым методам она является областью прикладной математики. Все попытки подхода к программированию как к технической дисциплине, а к созданию программ как к промышленному производству, неизменно терпели неудачу.
Заметим, что данное выше «определение» алгоритма достаточно расплывчато и, фактически, определением не является. В математике существует несколько вполне четких определений алгоритма, эквивалентных между собой, и большинство из них не слишком трудны для понимания. Все они, однако, требуют хорошего знания определенных областей математики и поэтому в начале мы не будем отвлекаться на (весьма важные и интересные) подробности, необходимые для строгого изложения понятия алгоритма. Вместо этого мы рассмотрим пример алгоритма, а потом перечислим основные свойства, которыми должен обладать любой алгоритм.
Подход, когда некоторое не до конца четко определенное понятие активно используют, в науке весьма типичен. Например, точные определения натуральных и действительных чисел не рассматривают ни только в средней школе, но даже и в большинстве ВУЗов. Более того, говорят, что сороконожка даже ходить разучилась, когда задумалась над тем, в каком порядке она переставляет ноги.
Пример и свойства алгоритма
Пусть нам нужно решить задачу нахождения наименьшего простого делителя натурального числа , большего единицы. Напомним, что простым называется число, не имеющее делителей, отличных от единицы и его самого, причем единица в множество простых чисел не входит. Вот как в этой книге мы будем записывать формулировки задач и их решения:
Задача 1.1. Придумайте алгоритм, вводящий натуральное число, большее единицы,который находит наименьший простой делитель этого числа.
Алгоритм решения задачи.
П1: Положить целое число равным двум и перейти на шаг П2.
П2: Если делится нацело на , то завершить работу алгоритма, выдав в качестве результата ; иначе перейти на шаг П3.
П3: Увеличить значение на единицу и перейти на шаг П2.
Для того чтобы понять этот алгоритм, надо выступить в роли компьютера (или скорее даже универсального исполнителя команд ), выполняя вручную указанную в нем последовательность действий для некоторых небольших значений . Будем записывать значения величины после каждого шага алгоритма.
| k = 3 | k = 4 | k = 2 |
| П1: i = 2 | П1: i = 2 | П1: i = 2 |
| П2: i = 2 | П2: i = 2 | П2: i = 2 |
| П3: i = 3 | ||
| П2: i = 3 |
Подобное исследование дает основание полагать, что после завершения работы алгоритма переменная действительно будет содержать наименьший простой делитель исходного числа . В данном случае это не сложно доказать и совершенно строго. Обязательно сделайте это.
Основные свойства любого алгоритма — это конечность, определенность, вход (ввод), выход (вывод) и эффективность. Рассмотрим их последовательно более подробно.
Конечность . Алгоритм должен всегда заканчиваться после выполнения конечного числа шагов. Алгоритм П удовлетворяет этому условию, так как величина
, ее значение увеличивается на единицу к каждому очередному выполнению шага П2, и поэтому выполнение алгоритма будет прекращено на шаге П2 при 
, если — простое число, или ранее при составном .
Определенность . Действия, которые необходимо произвести на каждом шаге, должны быть определены строго и недвусмысленно в каждом возможном случае. В данном примере применена достаточно определенная, хотя и не вполне формальная система обозначений. Чаще алгоритмы записывают с использованием более формальных алгоритмических языков, называемых также языками программирования , в которых каждое утверждение имеет точный смысл.
В настоящее время существует несколько тысяч языков программирования, десятки из них используется весьма активно. Такое большое число языков обусловлено разнообразием областей применения, различием в аппаратуре, для которой пишутся программы, и в уровне подготовки людей, их пишущих, а также существованием нескольких учений о том, как надо писать программы (так называемых парадигм программирования ).
Вход (input) . Алгоритм всегда имеет некоторое (иногда равное нулю) количество входных данных, то есть величин, передаваемых ему до начала работы. В алгоритме П, например, одна входная величина — целое число , большее единицы. Примером алгоритма, имеющего пустое множество входных данных, может служить алгоритм, вычисляющий 1000-е простое число.
Выход (output) . Алгоритм всегда обязан иметь одну или несколько выходных величин. В случае алгоритма П такой величиной является число . Алгоритмы, не имеющие выходных данных, бесполезны на практике, и мы не будем их изучать.
Эффективность . От алгоритма требуется, чтобы он был эффективным. Это означает, что все операции, которые необходимо произвести в алгоритме, должны быть достаточно простыми, чтобы их в принципе можно было выполнить точно и за конечное время с помощью карандаша и бумаги. В алгоритме П выполняются лишь следующие операции: сравниваются два целых числа, одно положительное число делится на другое, переменной присваивается значение целого числа два, ее значение увеличивается на единицу.
Все эти операции являются эффективными в указанном выше смысле, так как целые числа можно записать на бумаге конечным образом и существует по крайней мере по одному способу для деления и сложения двух целых чисел. Но те же самые операции не были бы эффективными, если бы значениями величин, фигурирующих в алгоритме, были бы произвольные действительные числа, выраженные бесконечными десятичными дробями, так как подобные величины нельзя даже записать на бумаге за конечное время.
Из вышесказанного следует, что на ЭВМ практически невозможно работать с действительными числами, что, по всей видимости, может показаться вам неправдоподобным. На самом деле это так. Более того, даже с настоящими целыми числами на компьютере работают не так уж и часто.
Обычно вместо множеств целых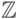 
и действительных 
чисел приходится работать с их заменителями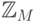 
и 
соответственно. Эти машинные аналоги часто вполне позволяют забыть о том, что мы имеем дело не с настоящими числами, но иногда особенности представления чисел в ЭВМ проявляются весьма неожиданным образом. Данной теме посвящена «лекция 4» курса.
Понятие эффективности алгоритма имеет и свои количественные характеристики. Различают временную и емкостную эффективности. Первая из них характеризует время выполнения алгоритма, а вторая — требуемый для этого объем памяти. Важнейшие для практики вопросы оценки временной эффективности или сложности (complexity) алгоритмов рассматриваются ниже, в «лекции 5» .
Источник: intuit.ru
Понятие алгоритма и программы. Принцип модульного программирования.
· один вход и один выход – на входе программный модуль получает определенный набор исходных данных, выполняет содержательную обработку и возвращает один набор результатных данных, т.е. реализуется стандартный принцип IPO (Input — Process — Output) – вход-процесс-выход;
· функциональная завершенность – модуль выполняет перечень регламентированных операций для реализации каждой отдельной функции в полном составе, достаточных для завершения начатой обработки;
· логическая независимость – результат работы программного модуля зависит только от исходных данных, но не зависит от работы других модулей;
· слабые информационные связи с другими программными модулями – обмен информацией между модулями должен быть по возможности минимизирован;
· обозримый по размеру и сложности программный элемент.
Принципы модульного программирования позволяют получать программные комплексы минимальной сложности, следующие:
· усиление внутренних связей в каждом модуле (иначе принцип называется повышением прочности модуля);
· ослабление взаимосвязи между модулями (иначе этот принцип называется ослаблением сцепления модулей).
Дата добавления: 2022-04-12 ; просмотров: 102 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник: poznayka.org