
1. Пример поэтапной разработки программы решения задачи
Информатика 10 класс
И. Г. Семакин
Е. К. Хеннер
Т. Ю. Шеина
Презентацию подготовила Камаева З. И.,
учитель информатики МБОУ гимназии №7
г. Красногорск Московской области
2.
Словом «задача» называют
проблему, которая требует решения
3.
Определение:
исходных данных
и
результатов
4.
Перевод задачи на язык математики –
формул, уравнений, систем неравенств и
т. п.
5.
Задача. Камень брошен вертикально вверх. Определить
через сколько секунд он достигнет высоты 60 м, если
начальная скорость камня была 40 м/с. Ускорение
свободного падения принять за 10 м/с ². Сопротивлением
воздуха пренебречь.
Постановка задачи
1.Постановка задачи.
Входные данные: высота(h),начальная скорость(υ₀),
ускорение свободного падения(¿);
результаты: время(t) .
2.Формализация задачи.
Движение камня равноускоренное, поэтому h = υ₀t — ¿ t ²/2
-¿ t ²/2 + υ₀t – h = 0 Подставим данные задачи в уравнение.
— 5t ²+ 40t – 60 = 0 Разделив его обе части на -5, получим
равносильное ему приведенное квадратное уравнение:
t ² — 8t + 12 = 0 .
6.
Определение всех вариантов множеств
значений исходных данных.
Определение для каждого варианта способа
решения и вида выходных данных
(результатов)
7.
Пример анализа решения квадратного
уравнения ax²+bx+c=0
8.
Определение структуры алгоритма,
последовательности команд.
Представление на каком-либо языке
описания алгоритмов (блок –схема,
учебный Алгоритмический язык)
9.
10.
Запись и отладка программы на
языке программирования.
Строгое соблюдение правил синтаксиса
языка.
11.
Программа решения квадратного уравнения на Паскале
Program Roots;
Var a,b,c,d,x1,x2: real;
Begin
Clrscr;
Write(‘введите коэффициенты кв. уравнения a,b,c:’);
readln(a,b,c);
If a=0
Then
If b=0
Then
If c=0
Then Writeln(‘Любое x — решение’)
Else Writeln(‘Нет решений’)
Else
Begin
x₁:=-cb;
Writeln(‘x=’, x)
End
Else
Begin
d:=b*b-4*a*c;
If d Then Writeln(‘Нет вещественных корней ‘)
Else
Begin
X1:=(-b+sqrt(d))/(2*a); x2:=(-b-sqrt(d))/(2*a);
Writeln(‘x1=’,x1′ x2=’,x2)
End
End
End.
12.
Экспериментальное доказательство
правильности алгоритма и работоспособности
программы.
Тест – вариант решения задачи с заданными
исходными данными, для которых известен
Решение задачи на компьютере. Последовательное конструирование алгоритма
результат.
План тестирования строится так, чтобы
наиболее полно проверить работу программы
13.
План и результаты тестирования
программы Roots
№
Исходные
значения
Верные
результаты
Результаты
тестирования
1
a=0, b=0, c=0
Любое x решение
Любое x решение
2
a=0, b=0, c=1
Нет решений
Нет решений
3
a=0, b=2, c=-6
X=3
X=3
4
a=2, b=1, c=-3
X1=1, x2=-1,5 X1=1, x2=-1,5
5
a=-1, b=-1, c=-2 Нет
Нет
вещественных вещественных
корней
корней
14. Сегодня узнали —
основные этапы разработки программы решения
задачи:
1.
2.
3.
4.
5.
6.
Постановка задачи
Формализация
Анализ математической задачи
Построение алгоритма
Составление программы
Тестирование
Источник: ppt-online.org
Информатика
Анализ, формальная постановка задачи и выбор метода решения

На данном этапе по результатам анализа условия задачи выбирают математические абстракции, адекватно, т.е. с требуемой точностью и полнотой, представляющие исходные данные и результаты, строят модель задачи и определяют метод преобразования исходных данных в результат (метод решения задачи). В этот раздел целесообразно включить два подраздела:
- Математическое описание возможных методов решения задачи, их ограничений и сравнительный анализ;
- Детального описание заданного метода, иллюстрация (если это возможно) на графике принципа его реализации, словесное описание последовательности действий, необходимых для получения результата, пример ручного счета для тестовой задачи.
На данном этапе по результатам анализа условия задачи выбирают математические абстракции, адекватно, т.е. с требуемой точностью и полнотой, представляющие исходные данные и результаты, строят модель задачи и определяют метод преобразования исходных данных в результат (метод решения задачи). Определив методы решения, следует для некоторых вариантов исходных данных вручную или на калькуляторе подсчитать ожидаемые результаты. Эти данные в дальнейшем будут использованы при тестировании программы. Кроме того, выполнение операций вручную позволяет точно уяснить последовательность действий, что упростит разработку алгоритмов. Целесообразно также продумать, для каких сочетаний исходных данных результат не существует или не может быть получен данным методом, что тоже необходимо учесть при разработке программы. ПримерМетодические указания не ставят целью приводить полное изложение примеров выполнения разделов. В приложении 1 приведено подробное описание методов решения для приведенного примера, которое после соответствующей переработки могут быть использованы в пояснительной записке курсовой работы. Подобные материалы имеются в рекомендованной литературе и в сети Интернет по всем вариантам заданий на выполнение курсовой работы. Разработать программу, которая с заданной точностью E находит значение аргумента х по заданному значению функции y(x) при известном значении n: y=(x+1) n +1/x, где n>1, x>0. Эта задача сводится к решению нелинейного уравнения вида y-(x+1) n +1/x=0. При n>1 данная функция является монотонно возрастающей. Для нахождения значения х можно применить метод половинного деления. Суть данного метода заключается в следующем. Вначале определяют отрезок [x1,x2] такой, что f(x1) < у < f(x2). Затем делят его пополам хt = (x1+x2)/2 и определяют, в какой половине отрезка находится х, для чего сравнивают f(хt) и у. Полученный отрезок опять делят пополам и так до тех пор, пока разность xj и x2 не станет меньше заданного значения E. Рассмотренный метод проиллюстрирован на рис.1. Рисунок 1. Графическое объяснение метода решения задачи Известно, что численное решение подобных задач выполняется в два этапа:
- Локализация корней;
- Уточнение корней.
Источник: studfile.net
Презентация, доклад на тему : Пример поэтапной разработки программы решения задачи
Слайд 1Пример поэтапной разработки программы решения задачи
Информатика 10 класс
И.
Г. Семакин
Е. К. Хеннер
Т. Ю. Шеина
Презентацию подготовила Камаева З. И.,
учитель информатики МБОУ гимназии №7
г. Красногорск Московской области

Слайд 2Словом «задача» называют проблему, которая требует решения

Слайд 31 этап

Слайд 42 этап
Перевод задачи на язык математики –
формул, уравнений,
систем неравенств и т. п.

Слайд 5Задача. Камень брошен вертикально вверх. Определить через сколько секунд он достигнет
высоты 60 м, если начальная скорость камня была 40 м/с. Ускорение свободного падения принять за 10 м/с ². Сопротивлением воздуха пренебречь.
1.Постановка задачи.
Входные данные: высота(h),начальная скорость(υ₀), ускорение свободного падения(¿);
результаты: время(t) .
2.Формализация задачи.
Движение камня равноускоренное, поэтому h = υ₀t — ¿ t ²/2 -¿ t ²/2 + υ₀t – h = 0 Подставим данные задачи в уравнение. — 5t ²+ 40t – 60 = 0 Разделив его обе части на -5, получим равносильное ему приведенное квадратное уравнение:
t ² — 8t + 12 = 0 .

Слайд 63 этап
АНАЛИЗ МАТЕМАТИЧЕСКОЙ ЗАДАЧИ
Определение всех вариантов множеств значений исходных данных.
каждого варианта способа решения и вида выходных данных (результатов)

Слайд 7Пример анализа решения квадратного уравнения ax²+bx+c=0

Слайд 84 этап
ПОСТРОЕНИЕ АЛГОРИТМА
Определение структуры алгоритма, последовательности команд.
Представление на каком-либо языке
описания алгоритмов (блок –схема, учебный Алгоритмический язык)

Слайд 9начало
конец
Ввод а,b,с
«Нет решений»
«Любое x»
«Нет вещественных корней»
Вывод x₁, x₂
а=0
d
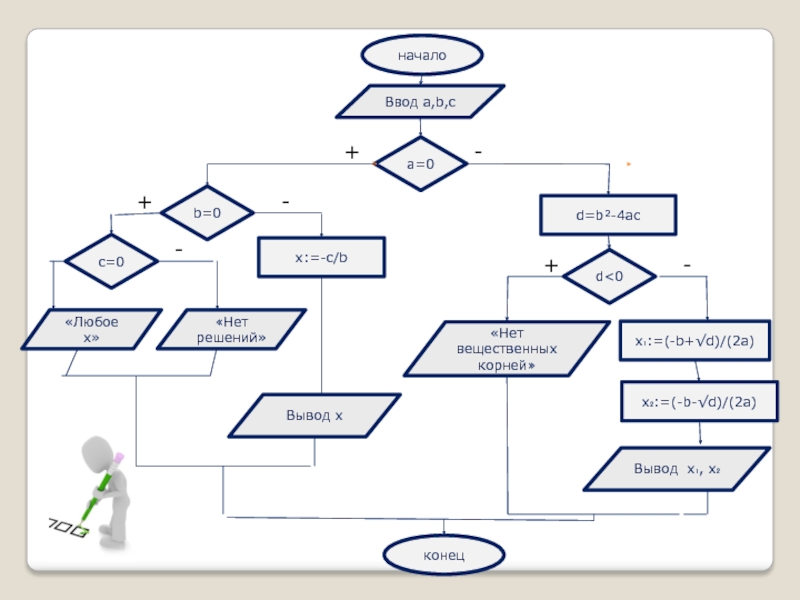
Слайд 105 этап
СОСТАВЛЕНИЕ ПРОГРАММЫ
Запись и отладка программы на языке программирования.
соблюдение правил синтаксиса языка.

Слайд 11Программа решения квадратного уравнения на Паскале
Program Roots;
Var a,b,c,d,x1,x2: real;
Begin
Clrscr;
Write(‘введите коэффициенты
кв. уравнения a,b,c:’);
readln(a,b,c);
If a=0
Then
If b=0
Then
If c=0
Then Writeln(‘Любое x — решение’)
Else Writeln(‘Нет решений’)
Else
Begin
x₁:=-cb;
Writeln(‘x=’, x)
End
Else
Begin
d:=b*b-4*a*c;
If d
Слайд 126 этап
ТЕСТИРОВАНИЕ
Экспериментальное доказательство правильности алгоритма и работоспособности программы.
вариант решения задачи с заданными исходными данными, для которых известен результат.
План тестирования строится так, чтобы наиболее полно проверить работу программы

Слайд 13План и результаты тестирования программы Roots
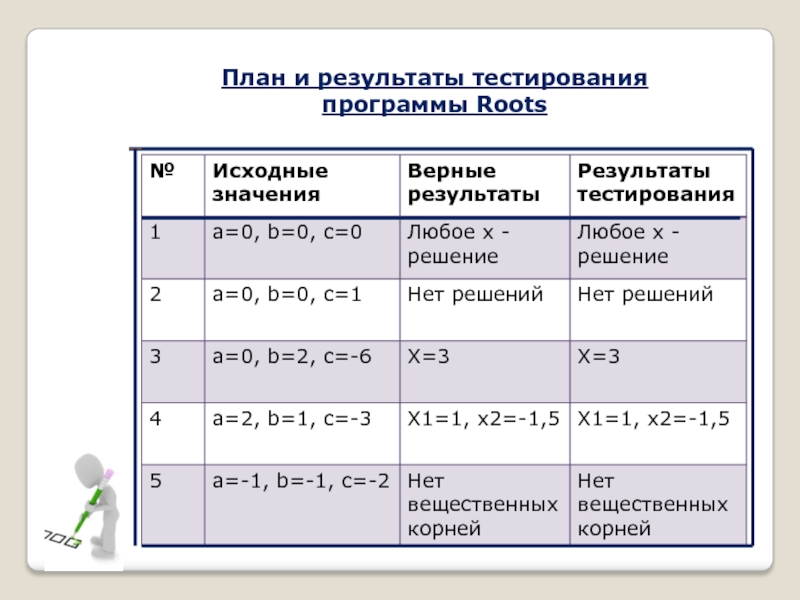
Слайд 14Сегодня узнали —
основные этапы разработки программы решения задачи:
1. Постановка задачи
2. Формализация
3. Анализ математической задачи
4. Построение алгоритма
5. Составление программы
6. Тестирование
Источник: shareslide.ru