Презентация на тему: » Проверка домашнего задания Нарисовать элементы блок-схем. 1.Начало или конец алгоритма 2.Ввод или вывод данных. 3.Процесс. 4.Проверка условия. 5.Направление.» — Транскрипт:
1 Проверка домашнего задания Нарисовать элементы блок-схем. 1.Начало или конец алгоритма 2.Ввод или вывод данных. 3.Процесс. 4.Проверка условия. 5.Направление.
2 Основные типы алгоритмическ их структур. 9 кл. Урок 3 17 сентября 2012 г.
3 Составить алгоритм для вычисления S Начало Ввод a,b.c Вывод S Конец
4 Составить алгоритм для вычисления k.Составить алгоритм для вычисления k. Начало Ввод a,b,c Вывод k Конец
5 Cсоставить алгоритм для вычисления k Начало Ввод a,b.c Вывод k Конец
6 Вычислить значение k для a=97 b=-4 с=3 c помощью калькулятора. 0, ,35233
7 Повторение. Написать алгоритм для вычисления площади трапеции.
8 Определите значение переменной a после выполнения фрагмента алгоритма. b:=b+1;a:=a*2; a:=1; b:=0; b = 4? да нет a:=1; b:=0; b:=b+1; a:=a*2; Задачи для тренировки:
Как по блок-схеме написать программу в python. Ветвление
9 Определите значение переменной m после выполнения фрагмента алгоритма. m:=54; 6 m=n? да нет m>n? да m:=m-n ; нет n:=n-m ; m:=54 n:=16
10 b:=b+1;a:=a*2; a:=1; b:=0; b = 4? a = 1? да нет a:=256; b:=0; a:=a/2; b:=b+a; Определите значение переменной b после выполнения фрагмента алгоритма.
11 Определите значения переменных x и y после выполнения фрагмента алгоритма. x:=10; y:=15; y
12 B З АДАНИЕ 1: З АПИШИТЕ ЗНАЧЕНИЕ ПЕРЕМЕННОЙ B ПОСЛЕ ВЫПОЛНЕНИЯ ФРАГМЕНТА АЛГОРИТМА. a:=a*2; b:=b+a; а:=1; b:=1; b>500? да нет
13 ab a:=1;1? b:=1;1 b > 500? нет a:=a*2; 2 b:=b+a; 3 b > 500? нет a:=a*2; 4 b:=b+a; 7 b > 500? нет a:=a*2; 8 b:=b+a; 15 b > 500? нет В ЫПОЛНИМ РУЧНУЮ ПРОКАТКУ.
14 ab a:=a*2; 256 b:=b+a; 511 b > 500? да
15 m:=54; n:=16; m = n ? да нет m > n? да m:=m-n; нет n:=n-m; З АДАНИЕ 3: О ПРЕДЕЛИТЬ ЗНАЧЕНИЕ ПЕРЕМЕННОЙ ПОСЛЕ ВЫПОЛНЕНИЯ ЦИКЛА
Источник: www.myshared.ru
Решение задач с блок схемами трассировка
Уроки 32 — 41
Оператор ветвления. Логические операции на Паскале
(§ 12. Алгоритмы с ветвящейся структурой. § 13. Программирование ветвлений на Паскале. § 14. Программирование диалога с компьютером)
Разработка программы на языке Паскаль с использованием оператора ветвления и логических операций
Уроки 32 — 33. Алгоритмы с ветвящейся структурой
Уроки 32 — 33
Алгоритмы с ветвящейся структурой





Блок-схемы

Представление ветвлений на АЯ. Трассировка ветвящихся алгоритмов
Рассмотрим несколько задач, решение которых на компьютере получается с помощью ветвящихся алгоритмов.
Первая задача: даны два числа; выбрать большее из них.
Пусть исходными данными являются переменные А и B. Их значения будут задаваться вводом. Значение большего из них должно быть присвоено переменной С и выведено на экран компьютера. Например, если А = 5, В = 8, то должно получиться: С = 8.
Блок-схема алгоритма решения этой задачи изображена на рис. 2.2.
Нетрудно понять смысл этого алгоритма. Если значение переменной А больше, чем В, то переменной С присвоится значение А. В противном случае, когда А ≤ B, переменной С присвоится значение B.
Условием, по которому разветвляется алгоритм, является отношение неравенства А > B. Изучая базы данных и электронные таблицы, вы узнали, что такое отношение является логическим выражением. Если оно справедливо, то результатом будет логическая величина «истина» и выполнение алгоритма продолжится по ветви «да»; в противном случае логическое выражение примет значение «ложь» и выполнение алгоритма пойдет по ветви «нет».
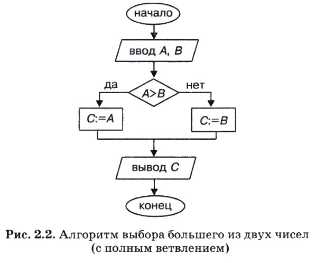
До выполнения на компьютере правильность алгоритма можно проверить путем заполнения трассировочной таблицы. Вот как будет выглядеть трассировка нашего алгоритма для исходных значений А = 5, В = 8.
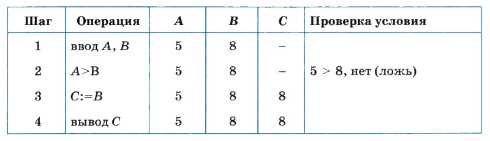
Ветвление является структурной командой. Его исполнение происходит в несколько шагов: проверка условия (выполнения логического выражения) и выполнение команд на одной из ветвей «да» или «нет». Поэтому в трассировочной таблице записываются не команды алгоритма, а отдельные операции, выполняемые компьютером на каждом шаге.
В алгоритме на рис. 2.2 используется полное ветвление. Эту же самую задачу можно решить, применяя структурную команду неполного ветвления. Блок-схема такого алгоритма изображена на рис. 2.3.
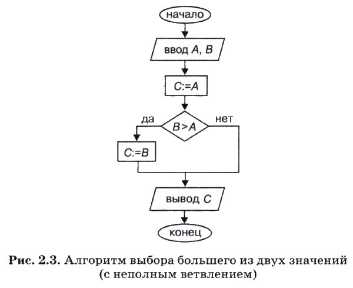
Выполните самостоятельно трассировку этого алгоритма для вариантов 1) А = 0,2, В = 0,3; 2) А = 7, Б = 4; 3) А = 5, В = 5. Если вы всё проделаете правильно, то убедитесь, что алгоритм верный.
А теперь запишем рассмотренные алгоритмы на АЯ. Во-первых, нужно решить вопрос о том, как описать переменные в этом алгоритме. Для всех переменных в алгоритме на АЯ необходимо указать их тип.
Переменные А, В, С — числовые величины. В этой задаче они могут принимать любые значения. В программировании числовые величины, которые могут иметь любые значения — целые, дробные, называются вещественными. Им ставится в соответствие вещественный тип. На АЯ этот тип указывается служебным словом вещ.
Как выглядит команда ветвления, вы уже знаете. Вот два алгоритма на АЯ, соответствующие блок-схемам на рис. 2.2 и 2.3.

Под сокращенным названием алгоритмов ВИД подразумевается «Большее из двух».
Для программирования характерно то, что одна и та же задача может быть решена с помощью разных алгоритмов. И чем сложнее задача, тем больше можно придумать различных алгоритмов ее решения. Для больших задач (производственных, научных) практически невозможно точное совпадение алгоритмов, составленных разными программистами.
Следующая задача: упорядочить значения двух переменных X и Y по возрастанию. Смысл этой задачи следующий: если для исходных значений переменных справедливо отношение X ≤ Y (например, X = 1, Y = 2), то оставить их без изменения; если же X > Y (например, X = 2, Y = 1), то выполнить обмен значениями.
Алгоритм обмена значениями двух переменных был рассмотрен в предыдущем параграфе. Вспомним, что для обмена мы использовали третью, вспомогательную переменную.
В алгоритме решения данной задачи используется неполное ветвление. Приведем блок-схему (рис. 2.4) и алгоритм на АЯ.
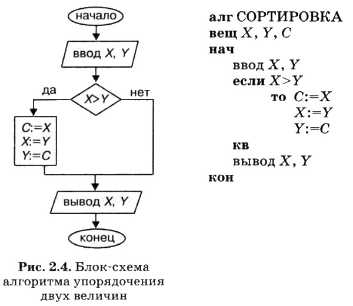
Здесь роль вспомогательной переменной для обмена выполняет С.


Следующая страница Уроки 32 — 33. Сложные ветвящиеся алгоритмы
Задачи на составление блок-схем алгоритмов

Задачи на составление блок-схем алгоритмов

Примеры определения результата выполнения алгоритма по заданной блок-схеме.
Пример 1. Дана блок-схема алгоритма

Определить результат выполнения алгоритма при определённых значениях исходных данных

Определить результат выполнения алгоритма при определённых значениях исходных данных
Например, при x= — 6 или x=0 или x=7
Проверка условия x>0 «Нет» y= -2*(-6)=12
Проверка условия x>0 «Нет» y=-2*0=0 Вывод: y=0
Проверка условия x>0 «Да» y=2*7=14 Вывод: y=14

Определить результат выполнения алгоритма при определённых значениях исходных данных
Например, при n=15 или n=0 или n=-7
Проверка условия n>0 «Нет» Проверка условия n 0 «Нет» Проверка условия n C «Нет» B=9+8=17; F=7+17=24 Вывод F=24
Проверка условия A=B «Да» С=6+6=12; F=6+12=18 Вывод F=18
Проверка условия A=B «Нет» Ю Проверка условия B>C «Да» Ю A=6+10=16; F=16+(-10)=6 Вывод F=6


Определить результат выполнения алгоритма при определённых значениях исходных данных
Алгоритмы с ветвящейся структурой Представление ветвлений на АЯ. Трассировка ветвящихся алгоритмов

Алгоритмы с ветвящейся структурой
Представление ветвлений на АЯ. Трассировка ветвящихся алгоритмов
Рассмотрим несколько задач, решение которых на компьютере получается с помощью ветвящихся алгоритмов.
Первая задача: даны два числа; выбрать большее из них.
Пусть исходными данными являются переменные А и В. Их значения будут задаваться вводом. Значение большего из них должно быть присвоено переменной С и выведено на экран компьютера. Например, если А = 5, В = 8, то должно получиться: С = 8.
Блок-схема алгоритма решения этой задачи изображена на рис. 3.6.

Рис. 3.6. Алгоритм выбора большего из двух чисел (с полным ветвлением)
Нетрудно понять смысл этого алгоритма. Если значение переменной А больше, чем В, то переменной С присвоится значение А. В противном случае, когда А В. Изучая базы данных и электронные таблицы, вы узнали, что такое отношение является логическим выражением. Если оно справедливо, то результатом будет логическая величина «истина» и выполнение алгоритма продолжится по ветви «да»; в противном случае логическое выражение примет значение «ложь» и выполнение алгоритма пойдет по ветви «нет».
До выполнения на компьютере правильность алгоритма можно проверить путем заполнения трассировочной таблицы. Вот как будет выглядеть трассировка нашего алгоритма для исходных значений А = 5, В = 8.
Ветвление является структурной командой. Его исполнение происходит в несколько шагов: проверка условия (выполнение логического выражения) и выполнение команд на одной из ветвей «да» или «нет». Поэтому в трассировочной таблице записываются не команды алгоритма, а отдельные операции, выполняемые компьютером на каждом шаге.
В алгоритме на рис. 3.6 используется полное ветвление. Эту же самую задачу можно решить, применяя структурную команду неполного ветвления. Блок-схема такого алгоритма изображена на рис. 3.7.

Рис. 3.7. Алгоритм выбора большего из двух значений (с неполным ветвлением)
Выполните самостоятельно трассировку этого алгоритма для вариантов 1) А = 0,2, В = 0,3; 2) А = 7, В = 4; 3) А = 5, В = 5. Если вы все проделаете правильно, то убедитесь, что алгоритм верный.
А теперь запишем рассмотренные алгоритмы на Алгоритмическом языке (АЯ). Во-первых, нужно решить вопрос о том, как описать переменные в этом алгоритме. Вспомним, что для всех переменных в алгоритме на Алгоритмическом языке необходимо указать их тип.
Переменные А, В, С — числовые величины. В этой задаче они могут принимать любые значения. В программировании числовые величины, которые могут иметь любые значения — целые, дробные, — называются вещественными. Им ставится в соответствие вещественный тип. На Алгоритмическом языке этот тип указывается служебным словом вещ.
Как выглядит команда ветвления, вы уже знаете. Вот два алгоритма на АЯ, соответствующие блок-схемам на рис. 3.6 и 3.7:
алг БИД1
вещ А, В, С
нач ввод А, В
если А>В
то С:=А
иначе С:=В
кв
вывод С
кон
алг БИД2
вещ А, В, С
нач ввод А, В
С:=А
если В>А
то С:=В
кв
вывод С
кон
Под сокращенным названием алгоритмов ВИД подразумевается «Большее из двух».
Для программирования характерно то, что одна и та же задача может быть решена с помощью разных алгоритмов. И чем сложнее задача, тем больше можно придумать различных алгоритмов ее решения. Для больших задач (производственных, научных) практически невозможно точное совпадение алгоритмов, составленных разными программистами.
Следующая задача: упорядочить значения двух переменных X и Y по возрастанию. Смысл этой задачи следующий: если для исходных значений переменных справедливо отношение X Y (например, X = 2, Y = 1), то выполнить обмен значениями.
Алгоритм обмена значениями двух переменных был рассмотрен в предыдущем параграфе. Вспомним, что для обмена нужна третья вспомогательная переменная.
В алгоритме решения данной задачи используется неполное ветвление. Приведем блок-схему (рис. 3.8) и алгоритм на АЯ.
алг СОРТИРОВКА
вещ X, Y, С
нач ввод X, Y
если X>Y
то С:=Х
Х:=Y
Y:=С
кв
вывод X, Y
кон

Рис. 3.8. Блок-схема алгоритма упорядочения двух величин
Здесь роль вспомогательной переменной для обмена выполняет С.
Решение задач с блок схемами трассировка
Трассировка
Для понимания чужой программы и для проверки правильности написания своей используют метод пошагового выполнения программы с отслеживанием значений всех переменных.
Пример 6.4.
Вычисление суммы чисел от 6 до 10
Рис. 6.3. Блок-схема алгоритма вычисления суммы чисел от 6 до 10
Для проверки правильности работы программы рекомендуется пошагово отслеживать изменение всех переменных после выполнения каждого оператора программы.
Такой процесс называется трассирввкой. Продемонстрируем этот прием (табл. 6.1).
В результате работы программы на экране получим число 40.
Таблица 6.1. Трассировка программы из примера 6.4
Для операторов, выполняющих проверку условий (if, for и т. п.) в столбце «Условие» принято указывать результат проверки. В данном случае в цикле for проверяется условие продолжения цикла.
Символы «. » подчеркивают, что значение счетчика цикла по выходе из цикла считается неопределенным.
Метод трассировки очень помогает при отладке программы, когда программа выдает не тот результат, который должна выдать. Осуществляя пошаговую трассировку, мы вникаем в логику работы программы и на каждом шаге проверяем, правильны ли были наши рассуждения при ее написании.
Вычисление суммы ряда
Рассмотрим задачу вычисления суммы ряда:
1/(1*1) + 1/(2*2) + 1/(3*3) + 1/(4*4) + 1/(5*5)
Здесь мы имеем ряд дробей, у которых в знаменателях записаны квадраты чисел от 1 до 5.
Рассмотрим каждую дробь как произведение двух дробей, например:
1/(3*3) = 1/3 * 1/3
В общем виде это можно записать так:
1/(N * N) = 1/N * 1/N
Блок-схема алгоритма решения задачи представлена на рис. 6.4.
Рис. 6.4. Блок-схема алгоритма вычисления суммы ряда
Задание 6.5.
Написать программу вычисления n! (факториал числа n), где n положительно. Определение факториала:
Другими словами, n! — это произведение первых n натуральных чисел.
Каждый следующий результат (обозначим его Р) получается путем умножения предыдущего результата (предыдущего Р) на счетчик, который пробегает значения от 1 до n.
Обозначим значение счетчика буквой k.
Получаем общий вид выражения: Р = Р * k (то есть воспользуемся рекуррентной формулой вычисления факториала: n! = (n — 1)! * n).
Программа должна быть организована так: с клавиатуры вводится число n (n— положительно), а затем на экран выдается таблица факториалов чисел до n включительно.
Задание 6.6.
Написать программу вычисления суммы ряда S=1 + 2 + 3 + 4 + 5 + 6. Нарисовать блок-схему и заполнить таблицу трассировки. Убедиться при трассировке, что сумма равна 21.
Таблица 6.2. Заготовка для таблицы трассировки алгоритма из задания 6.6
Источник: remnabor.net
Изображение алгоритма в виде блок-схемы

Блок-схемой называется наглядное графическое изображение алгоритма.
В блок-схеме отдельные этапы алгоритма изображают при помощи различных геометрических фигур – блоков.
Последовательность выполнения этапов указываются при помощи стрелок, соединяющих эти фигуры. Блоки сопровождаются надписями.
Типичные действия алгоритма изображаются следующими геометрическими фигурами:
Блок начала (конца) алгоритма
Надпись: «начало» («конец»).
Блок ввода-вывода данных
Надпись: «ввод» («вывод»)
и список переменных вводимых (выводимых).
Блок решения (арифметический)
Надпись: операция или группа операций.
Надпись: логическое условие.
2.3. Составной оператор
Это группа операторов, отделенных друг от друга точкой с запятой, начинающихся с открывающей фигурной скобки < и заканчивающихся закрывающейся фигурной скобкой >.
Транслятор воспринимает составной оператор как один оператор.
2.4. Операторы ветвления
Алгоритмы разветвленной структуры применяются, когда в зависимости от некоторого условия необходимо выполнить либо одно, либо другое действие.
Условный оператор, соответствующий приведенной блок-схеме, имеет вид:
if (выражение) оператор_1;
Вычисляется выражение. Если оно не равно нулю, т.е. имеет значение true, выполняется оператор_1, в противном случае (выражение равно нулю, т.е. false) – оператор_2.
Если в зависимости от некоторого условия выполняется некоторое действие, а в противном случае ничего не происходит, то алгоритм имет вид:
Условный оператор в этом случаеимет конструкцию:
if (выражение) оператор;
Эту запись можно назвать «пропуск оператора else».
Здесь оператор либо выполняется, либо пропускается, в зависимости от значения выражения.
Если в какой-либо ветви условного процесса требуется выполнить несколько операторов, следует использовать составной оператор.
2.5. Примеры программ
Задача 2. Известны коэффициенты а, b и с квадратного уравнения ax2+bx+c=0. Вычислить корни квадратного уравнения.
Входные данные: a, b, c.
Выходные данные: х1, х2.
printf(n vvedite a n);
Источник: csaa.ru