По традиционной программе натуральная последовательность вводится как

В начальном курсе математики под нумерацией будем понимать совокупность приемов обозначения и наименование натуральных чисел.

Натуральные числа изучаются по концентрам. Концентр – это объединенная по общим признакам область рассматриваемых чисел. В начальном курсе выделяют следующие концентры: десяток, сотня (2 этапа — от 11 до 20; от 21 до 100); тысяча, многозначные числа.

Конечная цель изучения нумерации – усвоение ряда общих принципов, лежащих в основе десятичной системы счисления, устной и письменной нумерации, подведение учащихся к систематическим обобщениям, умение выделять и подчеркивать то общее что обнаруживается в новой области чисел и рассмотрение нового на основе и в сравнении с ранее изученным.

Основными образовательными задачами изучения нумерации можно назвать:

1.Сформировать систему знаний:

— о натуральной последовательности;

— об устной и письменной нумерации;

2.Ознакомить с вычислительными приемами, основанными на знании нумерации.

Последовательности как найти закономерность.

При изучении данной темы у учащихся должны быть сформированы следующие умения:

1. читать любое число;

2. обозначать число письменно;

3. сравнивать любые числа разными способами;

4. заменять число суммой разрядных слагаемых;

5. дать характеристику любого числа.

Преемственность между концентрами увеличивает долю само­стоятельности учащихся при изучении нумерации чисел в каждом новом концентре.

Число тесно связано с измерением величин.

Понятие числа, разряда, класса формируется в процессе дей­ствий с различными множествами предметов. В качестве нагляд­ных пособий используются предметы, модели геометрических фигур, палочки, счеты, таблицы, абак.

Рассмотрим методику ознакомления с основными математическими понятиями, изучаемыми в данной теме.

Понятие натурального числа дается на эмпирическом уровне.

Число обозначается в порядке установления взаимно однозначного соответствия между предметами данной совокупности и словами – числительными.

В начальной школе:

1. Число – это количественная характеристика класса эквивалентных множеств.

2. Число – это элемент упорядоченного множества, член натуральной последовательности

3. При изучении действий число выступает как объект, над которым выполняется арифметическое действие.

У учащихся необходимо сформировать следующие знания и умения:

1.Выделить число из других понятий.

2.Правильно назвать число.

3.Знать способы образования числа (в результате счета; в результате измерения; в результате выполнения арифметических действий).

4.Знать способы обозначения чисел с помощью цифр.

Цифра – это знак для обозначения числа.

5.Знать различные функции числа. (Количественная функция, функция порядка, измерительная функция.)

Число и цифра 0.

1. Нуль рассматриваем как количественную характеристику класса пустых множеств (2-2, 4-4), т.е. множества, не содержащего ни одного элемента.

Порядок выполнения действий в выражениях. Числовые выражения

2. Нуль рассматриваем как цифру, обозначающую на линейке начало измерения (отмеривания).

3. Нуль рассматриваем как компонент действий I и II ступени (5+0, 0 ∙ 5).

4. Число нуль используется в том случае, если отсутствуют единицы какого-либо разряда (но не отсутствует разряд).

Например, в числе 300 отсутствуют единицы I и II разряда, т.е. единицы и десятки, обозначим число единиц и десятков нулями.

По традиционной программе натуральная последовательность вводится как ряд чисел, по которому ведется счет.

Свойства отрезка натурального ряда:

1. Натуральный ряд чисел начинается с единицы.

2. Каждое число имеет свое место. Каждое следующее число на единицу больше предыдущего; каждое предыдущее на единицу меньше последующего.

3. Все числа, стоящие до выделенного числа меньше его; все стоящие после – больше изученного числа.

4. Бесконечность натурального ряда чисел.

В натуральном ряду чисел учащиеся должны уметь выделить конечные последовательности: однозначных, двузначных, n-значных чисел.

9, 99, 999, 9999… — наибольшие однозначное, двузначное, трехзначное, четырехзначное, n-значное числа.

Почему? Если прибавим к каждому из них 1, то получим наименьшее число следующей последовательности.

10, 100, 1000, 10000 … — наименьшее двузначное, трехзначное, n – значное число, т. к. при вычитании из каждого единицы получим наибольшее число предыдущей последовательности.

Различают устную и письменную нумерацию.

Устная нумерация – совокупность правил, дающих возможность с помощью немногих слов составлять названия для многих чисел.

В ходе изучения устной нумерации необходимо раскрыть правила счета, чтения, образования чисел; знать цифры от 0 до 9, слова – числительные – сорок, девяносто, сто, тысяча, миллион, миллиард.

1. Считать надо все предметы, не пропуская ни одного и не повторяя один дважды.

2. Конечное число при счете относить ко всему множеству.

Экономика как подсистема общества: Может ли общество развиваться без экономики? Как побороть бедность и добиться.

Основные признаки растений: В современном мире насчитывают более 550 тыс. видов растений. Они составляют около.

В концентре «Сотня» изучаются следующие вопросы: нумерация чисел, сложение и вычитание, умножение и деление. Эти вопросы выделяются в особый концентр по следующим причинам:
— учащиеся знакомятся с новой счетной единицей — десятком и новым понятием — понятием разряда;
— учащиеся овладевают приемами устных и письменных вычислений на основе свойства арифметических действий, связи между их компонентами и результатом;
— учащиеся усваивают таблицы сложения и умножения и соответствующие случаи обратных действий — вычитания и деления;
— вводятся составные задачи и продолжается работа над простыми задачами;
— изучаются математические выражения, продолжается изучение геометрического материала.
В результате изучения нумерации в пределах 100, учащиеся должны овладеть следующими знаниями, умениями и навыками:
— научиться считать предметы десятками и усвоить образование, название двузначных чисел;
— усвоить порядок следования чисел при счете, используя предшествующее и последующее число;
— уметь сравнивать числа, опираясь на их место в натуральной последовательности, а также на десятичный состав чисел;
— уметь читать и записывать числа в пределах 100.
Нумерация в концентра «Сотня» изучается в два этапа: 1) устная нумерация; 2) письменная нумерация.
Подготовительной работой к изучению нумерации в пределах 10 является повторение нумерации в пределах 10: образование числа (присчитывание и отсчитывание по 1), последовательность чисел от 1 до 10, прямой и обратный счет. Каждый раз учитель говорит: эти же приемы мы будем использовать при изучении нумерации чисел больше 10, но там вместо единиц мы будем употреблять десятки.
Изучение устной нумерации в пределах 100 начинается с формирования у учащихся понятия о десятке. Предлагается отсчитать десять палочек и завязать их в пучок. Можно сказать «десять», «десяток» — т.е. десять единиц образуют десяток. Отсчитав по 10 палочек, мы получим еще 1 десяток и будет 2 десятка и т.д. Практически выясняем, что эти десятки можно сложить и вычитать как простые единицы.
После ознакомления с понятием «десяток», повторяем основные упражнения по образованию чисел в пределах 10 и то же самое проделываем используя термин «десяток»: считаем 1 десяток, 2 десятка, . и наоборот, выясняем: к 1 десятку прибавим 3 десятка, получим 4 десятка; из 7 десятков вычитаем 2 десятка, получим 5 десятков и т.д. Учащиеся должны понять, что при изучении
нумерации принципы и приемы работы с числами переходят из одного концентра в другое.
При изучении образования чисел от 11 до 20 из десятков и единиц может быть проведена такая практическая работа с дидактическим материалом: отсчитайте10 палочек, как сказать иначе, сколько у вас палочек? (1 десяток.) Завяжите палочки в пучок. Положите 1 палочку на десяток палочек. Сколько стало всего палочек? (Один – на — дцать.) Сколько здесь десятков палочек?

Возьмите десяток в левую руку и покажите. Покажите, сколько еще есть отдельных палочек. Значит, сколько десятков и единиц содержится в числе 11? Положите на десяток еще 1 палочку. Сколько палочек лежит на десятке? (Две.) Сколько всего палочек? Сколько десятков и сколько от дельных палочек?

Сколько единиц и сколько десятков в числе «две – на — дцать»?

ДОКЛАД ПО ДИСЦИПЛИНЕ

Направление 44.03.05 Педагогическое образование (с двумя профилями подготовки)

Направленность программы бакалавриата/магистратуры

Форма обучения заочная

В концентре «Сотня» изучаются следующие вопросы: нумерация чисел, сложение и вычитание, умножение и деление. Эти вопросы выделяются в особый концентр по следующим причинам:
— учащиеся знакомятся с новой счетной единицей — десятком и новым понятием — понятием разряда;
— учащиеся овладевают приемами устных и письменных вычислений на основе свойства арифметических действий, связи между их компонентами и результатом;
— учащиеся усваивают таблицы сложения и умножения и соответствующие случаи обратных действий — вычитания и деления;
— вводятся составные задачи и продолжается работа над простыми задачами;
— изучаются математические выражения, продолжается изучение геометрического материала.
В результате изучения нумерации в пределах 100, учащиеся должны овладеть следующими знаниями, умениями и навыками:
— научиться считать предметы десятками и усвоить образование, название двузначных чисел;
— усвоить порядок следования чисел при счете, используя предшествующее и последующее число;
— уметь сравнивать числа, опираясь на их место в натуральной последовательности, а также на десятичный состав чисел;
— уметь читать и записывать числа в пределах 100.
Нумерация в концентра «Сотня» изучается в два этапа: 1) устная нумерация; 2) письменная нумерация.
Подготовительной работой к изучению нумерации в пределах 10 является повторение нумерации в пределах 10: образование числа (присчитывание и отсчитывание по 1), последовательность чисел от 1 до 10, прямой и обратный счет. Каждый раз учитель говорит: эти же приемы мы будем использовать при изучении нумерации чисел больше 10, но там вместо единиц мы будем употреблять десятки.
Изучение устной нумерации в пределах 100 начинается с формирования у учащихся понятия о десятке. Предлагается отсчитать десять палочек и завязать их в пучок. Можно сказать «десять», «десяток» — т.е. десять единиц образуют десяток. Отсчитав по 10 палочек, мы получим еще 1 десяток и будет 2 десятка и т.д. Практически выясняем, что эти десятки можно сложить и вычитать как простые единицы.
После ознакомления с понятием «десяток», повторяем основные упражнения по образованию чисел в пределах 10 и то же самое проделываем используя термин «десяток»: считаем 1 десяток, 2 десятка, . и наоборот, выясняем: к 1 десятку прибавим 3 десятка, получим 4 десятка; из 7 десятков вычитаем 2 десятка, получим 5 десятков и т.д. Учащиеся должны понять, что при изучении
нумерации принципы и приемы работы с числами переходят из одного концентра в другое.
При изучении образования чисел от 11 до 20 из десятков и единиц может быть проведена такая практическая работа с дидактическим материалом: отсчитайте10 палочек, как сказать иначе, сколько у вас палочек? (1 десяток.) Завяжите палочки в пучок. Положите 1 палочку на десяток палочек. Сколько стало всего палочек? (Один – на — дцать.) Сколько здесь десятков палочек?

Возьмите десяток в левую руку и покажите. Покажите, сколько еще есть отдельных палочек. Значит, сколько десятков и единиц содержится в числе 11? Положите на десяток еще 1 палочку. Сколько палочек лежит на десятке? (Две.) Сколько всего палочек?

Сколько десятков и сколько от дельных палочек? Сколько единиц и сколько десятков в числе «две – на — дцать»?

1. Подготовительный период к изучению нумерации чисел (вводные уроки математики).

2. Методика изучения нумерации чисел первого десятка.

3. Методика изучения нумерации чисел в пределах 100:

а) числа от 11 до 20;

б) числа от 21 до 100.

4. Методика изучения нумерации чисел в пределах 1000.

5. Методика изучения нумерации многозначных чисел.

Из курса математики известно, что системой счисления называют язык для наименования чисел, их записи и выполнения действий над ними. Различают позиционные и непозиционные системы счисления. В позиционных системах один и тот же знак (из принятых в данной системе) может обозначать различные числа в зависимости от места (позиции), занимаемого этим знаком в записи числа.

Например, в числе 29 цифра 9 обозначает количество единиц, а в числе 97 – количество десятков.

В непозиционных системах каждый знак обозначает одно и то же число, независимо от позиции (например, римские цифры: I – 1, V – 5, X – 10, L – 50, C – 100, D – 500, M – 1000).

Умения, а затем и навыки, читать и записывать числа в десятичной системе счисления формируется у младших школьников поэтапно и тесно связано с такими понятиями, как число, цифра, разряд, класс, разрядные единицы, разрядные десятки, разрядные сотни и т.д., разрядные слагаемые.

После разложения предметов на две группы устанавливается количество элементов в каждом подмножестве путем пересчета. Количество элементов в каждой группе обозначается цифрой и обобщается: как можно получить число 4? Действия математизируются.

После изучения чисел от 1 до 10 вводится число 0. Число 0 является характеристикой пустого множества, т.е. множества, не содержащего ни одного элемента. Для того чтобы учащиеся могли представить себе такое множество, предлагаются упражнения в отсчитывании предметов по одному до тех пор, пока не останется ни одного предмета (облетают листья с ветки, улетают птицы из гнезда, ученик отдает тетради и т.д.).

— На веточке 3 листочка. Подул ветер и один листочек улетел. Сколько осталось? (3-1=2).

— Увеличилось или уменьшилось количество листочков? (уменьшилось).

— Сколько листочков останется, если упадет еще один? (число листочков уменьшится еще на один. 2-1=1).

— Сколько листочков останется, если и последний улетит? (нисколько, 0, 1-1=0).

— Число, которое записывают при помощи цифры 0, показывает, что ни одного листочка не осталось.

Таким образом, 0 вводится как результат вычитания.

Другой методический прием связан с установлением соответствия между числовой фигурой (или рисунком) и цифрой, обозначающей количество предметов.

Этим подходом можно воспользоваться до изучения сложения и вычитания, на этапе формирования представлений о количественном числе.

Возможен и такой подход, при котором 0 является не только результатом вычитания, но выступает компонентом действия сложения. Для этой цели предлагается задание:

Что изменилось?

Дети обычно отвечают: ничего не изменилось.

— Может, кто-нибудь догадается, какую математическую запись можно использовать для этого случая? (5+0=5, 5-0=5).

После знакомства с числом 0 переходят к его сравнению с другими числами. Например, опираясь на решение задачи про листья, выясняют, сколько листьев было, сколько упало, больше или меньше листьев стало после того, как один упал. Результат сравнения записывают:

2 99). Этим самым сравнение чисел в пределах 1000 сводится к сравнению трехзначных чисел.

На примерах выясняется, что из двух трехзначных чисел то больше, у которого цифра сотен больше (321 > 285, 505 > 396 и т. п.). Если же цифры сотен двух сравниваемых чисел равны, то сравниваются цифры десятков, и то число больше, у которого цифра десятков больше (485 > 478, 315 > 308 и т. п.). Если же и цифры десятков равны, то сравниваются цифры единиц, и то число больше, у которого цифра единиц больше (576 > 572, 105 > 101 и т. п.).

Два трехзначных числа равны тогда и только тогда, когда цифры их одноименных разрядов (сотен, десятков, единиц) равны (одинаковы).

Описанный алгоритм можно представить (для учителя, конечно) в виде схемы.

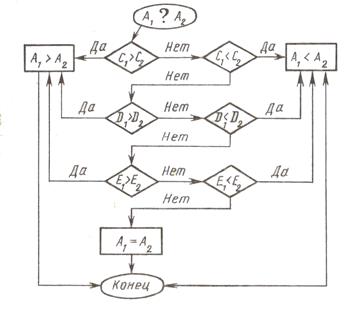
Пусть необходимо сравнить два трёхзначных числа:

цифры сотен, десятков и единиц числа А2

Однако эта схема алгоритма построена нерационально, хотя по дидактическим соображениям более понятна. Циклический характер процесса сравнения отражается в более простой схеме

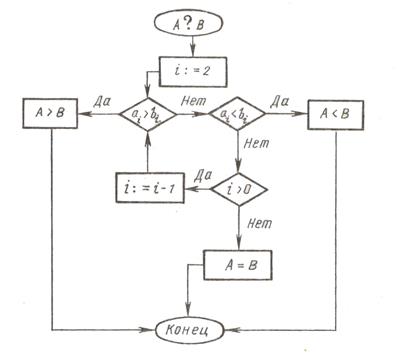
Введем следующие обозначения: А и В — сравниваемые числа

Этот алгоритм легко обобщается для сравнения двух многозначных чисел: А = апап-1. а0, B = bmbm-1. b1b0

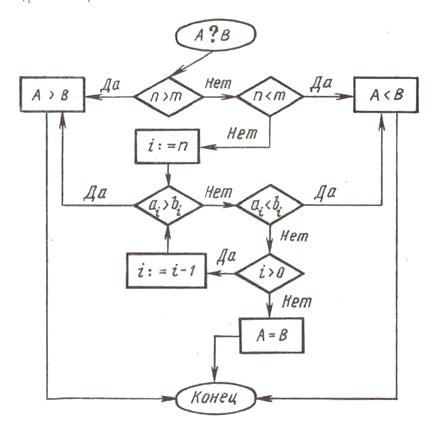
Методика изучения нумерации целых неотрицательных чисел

1. Подготовительный период к изучению нумерации чисел (вводные уроки математики).

2. Методика изучения нумерации чисел первого десятка.

3. Методика изучения нумерации чисел в пределах 100:

а) числа от 11 до 20;

б) числа от 21 до 100.

4. Методика изучения нумерации чисел в пределах 1000.

5. Методика изучения нумерации многозначных чисел.

Из курса математики известно, что системой счисления называют язык для наименования чисел, их записи и выполнения действий над ними. Различают позиционные и непозиционные системы счисления. В позиционных системах один и тот же знак (из принятых в данной системе) может обозначать различные числа в зависимости от места (позиции), занимаемого этим знаком в записи числа.

Например, в числе 29 цифра 9 обозначает количество единиц, а в числе 97 – количество десятков.

В непозиционных системах каждый знак обозначает одно и то же число, независимо от позиции (например, римские цифры: I – 1, V – 5, X – 10, L – 50, C – 100, D – 500, M – 1000).

Умения, а затем и навыки, читать и записывать числа в десятичной системе счисления формируется у младших школьников поэтапно и тесно связано с такими понятиями, как число, цифра, разряд, класс, разрядные единицы, разрядные десятки, разрядные сотни и т.д., разрядные слагаемые.

Подходы к построению урока математики. Количественная характеристика натуральных чисел. Изучение десятичной системы счисления. Формирование представлений о смысле сложения и вычитания целых неотрицательных чисел. Изучение действий умножения и деления.

Рубрика	Педагогика
Вид	контрольная работа
Язык	русский
Дата добавления	04.05.2009
Размер файла	27,1 K

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

• Система трансцендентального идеализма шеллинга кратко
• Требования к мебели зала микробиология кратко
• Справка о работе школьного музея боевой славы
• Сценарий юбилея детского сада 55 лет интересный
• Религия древней месопотамии кратко презентация

Источник: obrazovanie-gid.ru

Вопрос 3

В начальном курсе математики под нумерацией будем понимать совокупность приемов обозначения и наименования натуральных чисел.

Натуральные числа изучаются по концентрам. Концентр — это объединенная по общим признакам область рассматриваемых чисел. В начальном курсе выделяют следующие концентры: десяток, сотня (2 этапа — от 11 до 20; от 21 до 100); тысяча, многозначные числа.

Конечная цель изучения нумерации — усвоение ряда общих принципов, лежащих в основе десятичной системы счисления, устной и письменной нумерации, подведение учащихся к систематическим обобщениям, умение выделять и подчеркивать то общее, что обнаруживается в новой области чисел, и рассмотрение нового на основе и в сравнении с ранее изученным.

Основными образовательными задачами изучения нумерации можно назвать:

1. Сформировать систему знаний:

— о натуральном числе и числе «0»;

— о натуральной последовательности;

— об устной и письменной нумерации.

2. Ознакомить с вычислительными приемами, основанными на знании нумерации.

При изучении данной темы у учащихся должны быть сформированы следующие умения:

— читать любое число;

— обозначать число письменно;

— сравнивать любые числа разными способами;

— заменять число суммой разрядных слагаемых;

— дать характеристику любого числа.

Рассмотрим методику ознакомления с основными математическими понятиями, изучаемыми в данной теме.

Понятие натурального числа дается на эмпирическом уровне.

Число обозначается в порядке установления взаимно-однозначного соответствия между предметами данной совокупности и словами — числительными.

В начальной школе:

1. Число — это количественная характеристика класса эквивалентных множеств.
2. Число — это элемент упорядоченного множества, член натуральной последовательности.
3. При изучении действий число выступает как объект, над которым выполняется арифметическое действие.

1. Натуральный ряд чисел начинается с единицы.
2. Каждое число имеет свое место. Каждое следующее число на единицу больше предыдущего; каждое предыдущее на единицу меньше последующего.
3. Все числа, стоящие до выделенного числа, меньше его; стоящие после — больше изученного числа.
4. Бесконечность натурального ряда чисел.

1. Считать надо все предметы, не пропуская ни одного и не повторяя один дважды.
2. Конечное число при счете относить ко всему множеству.

1. Непозиционная система, которая характеризуется тем, что каждому знаку независимо от формы записи числа приписывается одно вполне определенное значение (например, римская нумерация).
2. Позиционная система (например, десятичная система счисления), которая характеризуется следующими свойствами:

• Каждая цифра принимает различные значения в зависимости от ее положения в записи числа (позиционный принцип записи).
• Каждая цифра в зависимости от ее положения называется разрядной единицей; разрядные единицы следующие: единицы, десятки, сотни и т.д.
• 10 единиц одного разряда составляют одну единицу следующего разряда, т.е. соотношение разрядных единиц равно десяти (10 ед. = 1 дес.; 10 дес. = 1 сот. и т.д.).
• Начиная справа налево и подряд, каждые 3 разрядные единицы образуют разрядные классы (единиц, тысяч, миллионов и др.).
• Прибавление к девяти единицам еще одной единицы данного разряда дает единицу следующего, более высшего (старшего) разряда.

1. Счетная единица — то, что берем за основу счета. Каждая следующая счетная единица больше предшествующей в 10 раз.
2. Разряд — место цифры в записи числа.

1. сначала рассматривается образование счетной единицы, ведется счет предметов с помощью этой счетной единицы;
2. на основе счета вводятся новые разрядные числа, раскрывается их образование и названия;
3. на основе счета с помощью всех известных счетных единиц показывается образование и устное обозначение неразрядных чисел; их состав из разрядных;
4. включаются упражнения в счете предметов с использованием новых чисел; усваивается натуральная последовательность чисел;
5. на основе знания десятичного состава и поместного значения цифр раскрывается письменная нумерация чисел;
6. во всех концентрах наряду со счетом рассматривается измерение таких величин, как длина, масса, стоимость; единицы измерения этих величин и их соотношение изучаются в сопоставлении с соответствующими счетными единицами и помогают их усвоению, (например, 1 дм = 10 см; 1 р. = 100 к.; 1 кг = 1000 г и т.д.);
7. вводятся способы сравнения чисел на основе:

• принципа образования натуральной последовательности;
• установления взаимно-однозначного соответствия между элементами множеств;
• знания разрядного состава чисел;

• знания классового состава;

1. в каждом концентре вводятся вычислительные приемы, основанные на знании нумерации:

1. Чтение числа.
2. Место числа при счете.
3. Десятичный состав.
4. Запись числа с помощью цифр.

Источник: studfile.net

Тема: Изучение целых неотрицательных чисел.

В начальном курсе математики под нумерацией будем понимать совокупность приемов обозначения и наименование натуральных чисел.

Натуральные числа изучаются по концентрам. Концентр – это объединенная по общим признакам область рассматриваемых чисел. В начальном курсе выделяют следующие концентры: десяток, сотня (2 этапа — от 11 до 20; от 21 до 100); тысяча, многозначные числа.

Конечная цель изучения нумерации – усвоение ряда общих принципов, лежащих в основе десятичной системы счисления, устной и письменной нумерации, подведение учащихся к систематическим обобщениям, умение выделять и подчеркивать то общее что обнаруживается в новой области чисел и рассмотрение нового на основе и в сравнении с ранее изученным.

Основными образовательными задачами изучения нумерации можно назвать:

1.Сформировать систему знаний:

— о натуральном числе и числе «0»;

— о натуральной последовательности;

— об устной и письменной нумерации;

2.Ознакомить с вычислительными приемами, основанными на знании нумерации.

При изучении данной темы у учащихся должны быть сформированы следующие умения:

1. читать любое число;

2. обозначать число письменно;

3. сравнивать любые числа разными способами;

4. заменять число суммой разрядных слагаемых;

5. дать характеристику любого числа.

Изучение нумерации чисел в курсе математики начальных клас­сов строится по концентрам: «Десяток», «Сотня», «Тысяча», «Многозначные числа». Это позволяет неоднократно возвращаться к основным вопросам темы, совершенствуя тем самым знания и умения учащихся.

Преемственность между концентрами увеличивает долю само­стоятельности учащихся при изучении нумерации чисел в каждом новом концентре.

В основе чтения и записи чисел лежит усвоение таких поня­тий, как «число», «цифра», «разряд», «класс».

В основе формирования понятия числа в школе лежит счет предметов. Счет служит для определения количества. Число выс­тупает как результат счета, т. е. число, названное последним при счете, характеризует количество предметов данной совокупности (количественное число).

В основе операции счета лежит установ­ление взаимно однозначного соответствия между предметами дан­ной совокупности и словами-числительными, которые называются в определенном порядке. Поэтому каждое число, названное при счете, характеризует не только количество предметов данной совокупности, но и порядок их при счете (порядковое число). Поэто­му число как общая характеристика класса эквивалентных множеств осознается ребенком в процессе установления взаимно однознач­ного соответствия между элементами различных множеств. Ответы на вопросы: «Больше?», «Меньше?», «Столько же?» — могут быть получены с помощью счета и при помощи установления взаимно однозначного соответствия между предметами.

Число тесно связано с измерением величин.

Центральным вопросом темы «Нумерация» является усвоение принципа образования чисел в натуральном ряду, суть которого разъясняется учащимся на наглядном материале в тесной взаимосвя­зи с операцией счета.

Понятие цифры как знака для записи чисел вводится в кон­центре «Десяток» и используется для записи чисел в последующих концентрах.

Понятие разряд разъясняется детям в концентре «Сотня» и используется в последующих концентрах. При изучении нумера­ции многозначных чисел учащиеся знакомятся с понятием класс.

Понятие числа, разряда, класса формируется в процессе дей­ствий с различными множествами предметов. В качестве нагляд­ных пособий используются предметы, модели геометрических фигур, палочки, счеты, таблицы, абак.

Рассмотрим методику ознакомления с основными математическими понятиями, изучаемыми в данной теме.

Понятие натурального числа дается на эмпирическом уровне.

Число обозначается в порядке установления взаимно однозначного соответствия между предметами данной совокупности и словами – числительными.

В начальной школе:

1. Число – это количественная характеристика класса эквивалентных множеств.

2. Число – это элемент упорядоченного множества, член натуральной последовательности

3. При изучении действий число выступает как объект, над которым выполняется арифметическое действие.

У учащихся необходимо сформировать следующие знания и умения:

1.Выделить число из других понятий.

2.Правильно назвать число.

3.Знать способы образования числа (в результате счета; в результате измерения; в результате выполнения арифметических действий).

4.Знать способы обозначения чисел с помощью цифр.

Цифра – это знак для обозначения числа.

5.Знать различные функции числа. (Количественная функция, функция порядка, измерительная функция.)

Число и цифра 0.

1. Нуль рассматриваем как количественную характеристику класса пустых множеств (2-2, 4-4), т.е. множества, не содержащего ни одного элемента.

2. Нуль рассматриваем как цифру, обозначающую на линейке начало измерения (отмеривания).

3. Нуль рассматриваем как компонент действий I и II ступени (5+0, 0 ∙ 5).

4. Число нуль используется в том случае, если отсутствуют единицы какого-либо разряда (но не отсутствует разряд).

Например, в числе 300 отсутствуют единицы I и II разряда, т.е. единицы и десятки, обозначим число единиц и десятков нулями.

По традиционной программе натуральная последовательность вводится как ряд чисел, по которому ведется счет.

Свойства отрезка натурального ряда:

1. Натуральный ряд чисел начинается с единицы.

2. Каждое число имеет свое место. Каждое следующее число на единицу больше предыдущего; каждое предыдущее на единицу меньше последующего.

3. Все числа, стоящие до выделенного числа меньше его; все стоящие после – больше изученного числа.

4. Бесконечность натурального ряда чисел.

В натуральном ряду чисел учащиеся должны уметь выделить конечные последовательности: однозначных, двузначных, n-значных чисел.

9, 99, 999, 9999… — наибольшие однозначное, двузначное, трехзначное, четырехзначное, n-значное числа.

Почему? Если прибавим к каждому из них 1, то получим наименьшее число следующей последовательности.

10, 100, 1000, 10000 … — наименьшее двузначное, трехзначное, n – значное число, т. к. при вычитании из каждого единицы получим наибольшее число предыдущей последовательности.

Различают устную и письменную нумерацию.

Устная нумерация – совокупность правил, дающих возможность с помощью немногих слов составлять названия для многих чисел.

В ходе изучения устной нумерации необходимо раскрыть правила счета, чтения, образования чисел; знать цифры от 0 до 9, слова – числительные – сорок, девяносто, сто, тысяча, миллион, миллиард.

1. Считать надо все предметы, не пропуская ни одного и не повторяя один дважды.

2. Конечное число при счете относить ко всему множеству.

Источник: poisk-ru.ru