Площадь треугольника программа какого класса

Учебник: Математика. 5 класс: учебник для учащихся общеобразовательных учреждений / И.И. Зубарева, А.Г. Мордкович. — М.: Мнемозина, 2013.

Тема урока: Площадь треугольника

Тип урока: Урок ознакомления с новым материалом.

Скачать:

Предварительный просмотр:

Предмет: математика, 5 класс

Учитель: Васильева Елена Викторовна, учитель математики, М.О. г. Лобня МБОУ СОШ №9

Учебник : Математика. 5 класс: учебник для учащихся общеобразовательных учреждений / И.И. Зубарева, А.Г. Мордкович. — М.: Мнемозина, 2013.

Тема урока : Площадь треугольника

Тип урока : Урок ознакомления с новым материалом.

Содержательная цель: расширение знаний учащихся за счет знакомства с новой формулой.

Деятельностная цель: формирование у учащихся навыков нахождения площади треугольника при помощи формулы S = (ah) : 2.

Планируемые результаты: обучающиеся научатся находить площадь треугольника по формуле: S = (ah):2 ; строить высоты, выходящие из всех углов треугольника, составлять алгоритм действий, рассуждать и делать выводы; слушать собеседника и вести диалог; работать в паре; излагать свою точку зрения; аргументированно отвечать на вопросы собеседников, оценивать себя и товарищей.

8 класс, 14 урок, Площадь треугольника

— формирование познавательных УУД :

научить в процессе реальной ситуации использовать определения следующих понятий: «площадь треугольника», вычислять площади треугольников по формуле. Решать задачи.

— формирование коммуникативных и личностных УУД :

умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, воспитывать ответственность и аккуратность.

— формирование регулятивных УУД:

1. развивать умение анализировать, сравнивать, обобщать, делать выводы, развивать внимание, формировать коммуникативную компетенцию учащихся; выбирать способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.
2. Используемые технологии: проблемное обучение, технология сотрудничества, уровневая дифференциация

• по источникам знаний: словесные, наглядные;
• по степени взаимодействия учитель-ученик: эвристическая беседа;
• относительно дидактических задач: подготовка к восприятию;
• относительно характера познавательной деятельности: репродуктивный, частично-поисковый.

Формы работы учащихся: фронтальная, парная, индивидуальная.

Организация деятельности учащихся на уроке:

-самостоятельно выходят на проблему и решают её;

-самостоятельно определяют тему, цели урока;

-выводят правило вычисления площади треугольника, алгоритм вычисления площади треугольника;

-работают с текстом учебника;

-отвечают на вопросы;

-решают самостоятельно задачи;

-оценивают себя и друг друга;

Необходимое техническое оборудование: Компьютер, проектор, учебники по математике, раздаточный материал (карточки с дополнительным заданием, карточки с домашним заданием), электронная презентация, выполненная в программе Power Point

ФОРМУЛА ГЕРОНА. Площадь треугольника #shorts

1. Организационный момент (1 минута)

Добрый день, ребята!

Французский писатель XIX века Анатоль Франц однажды заметил, что:
«Учиться можно только весело. Чтобы переваривать эти знания, нужно поглощать их с аппетитом».

Давайте сегодня на уроке будем следовать этому совету. Будем активны, будем поглощать знания с большим желанием, потому что они пригодятся вам в дальнейшей жизни.

1. Актуализация опорных знаний (6 минут)

Давайте вспомним, чем мы с вами занимались на последних занятиях, какую геометрическую фигуру изучали? / Треугольник/

1. Что называют треугольником? / треугольник – геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, последовательно соединяющих эти точки/
2. Какие виды треугольников вы знаете? / остроугольный, тупоугольный, прямоугольный/
3. Что называется периметром треугольника? / Сумма длин его сторон/
4. Верно ли, что треугольник, у которого все углы прямые, называется прямоугольным? /нет , неверно /
5. Объясните, какой треугольник называют прямоугольным? / Прямоугольный треугольник – это треугольник, в котором есть прямой угол/
6. Как найти площадь прямоугольного треугольника? / Площадь прямоугольного треугольника равна половине произведения катетов (сторон, образующих прямой угол).

Математический диктант по вариантам с взаимопроверкой в парах.

1. Определите вид треугольника
2. Найдите периметр треугольника
3. Вычислите площадь прямоугольного треугольника

1. Изучение нового материала (15 минут)

— Внимание на экран. Здесь изображена аппликация парусника из цветной бумаги. Из каких частей он состоит? /Из лодки и паруса/

-А из каких геометрических фигур? / Из прямоугольника, прямоугольных треугольников и произвольного треугольника/

-Поработайте в парах и попробуйте найти площадь его частей, а затем и общую площадь этого парусника. Его образец лежит у вас на столах.

-Какие результаты у вас получились?

-Где возникло затруднение? / при вычислении площади паруса/

-Какими способами можно вычислить площадь этого треугольника?

/ Могут предложить достроить до прямоугольника и посчитать по клеткам/.

-Всегда ли так удобно вычислять площадь фигур? / Не всегда удобно /

-Что использовали при вычислении площади прямоугольника и прямоугольного треугольника (лодки)? / Использовали формулы/

-Можем ли мы использовать эти формулы при вычислении площади паруса?

/ Нет, т.к. нет прямого угла/

-Как вы думаете, чем мы будем заниматься сегодня на уроке / учиться вычислять площадь произвольного треугольника/

-Сформулируйте тему нашего урока

Тема урока: « Площадь произвольного треугольника»

-Откройте тетрадь. Число, тема урока. Положите авторучки.

— А из какого источника мы будем «добывать» наши новые знания / читать учебник /

— Откройте учебник на стр.156 и выполните №568

Площадь треугольника равна половине площади прямоугольника, длина которого равна стороне АС треугольника, а ширина- отрезку ВD.

Как вычислить площадь треугольника, не достраивая каждый раз его до прямоугольника? Какие будут ваши предложения? /Разобьем треугольник на два прямоугольных треугольника с помощью отрезка BD, проведенного под прямым углом к отрезку АС/

Да, и этот отрезок, проведенный к стороне под прямым углом, называют высотой.

Прочитайте определение на стр.156.

Сделаем рисунок в тетрадях:

Нарисуйте треугольник ABC. Из вершины В к противоположной стороне проведем отрезок BD под прямым углом.

— Каким чертежным инструментом надо воспользоваться для построения прямого угла? /Угольником/

Высоту обозначим буквой h . Длину отрезка АС обозначим буквой а. Как известно площадь обозначается буквой S . Используя эти обозначения, постарайтесь записать формулу площади треугольника.

(один учащийся пишет на доске)

Проговорите . Возможен вариант:

Площадь треугольника равна произведению высоты на сторону, к которой проведена высота, деленному на два.

Записать: Площадь треугольника равна половине произведения стороны и высоты, проведенной к этой стороне.

А теперь попробуйте сформулировать алгоритм действий для нахождения площади треугольника, т.е. пошаговую инструкцию. Этот алгоритм соответствует тому алгоритму, который лежит у вас на столах.

1. Выбрать вершину треугольника, из которой будем проводить высоту
2. Проводим высоту к противоположной стороне
3. Измеряем высоту
4. Измеряем сторону, к которой проведена высота
5. Вычисляем по формуле S= (a∙h):2

1. Закрепление изученного материала (7 минут)

1. Физкультминутка (2 минуты)

А сейчас, ребята, немного отвлечемся и поиграем в «истинно – ложно». Встаньте, пожалуйста.

Если утверждение истинно, то поднимаем руки вверх, если ложно, то руки в стороны.

• Делить на нуль нельзя
• Развернутый угол равен 90°

• В слове биссектриса три буквы «с»
• 6∙6=46
• Острый угол меньше 90°

Отдохнули? Садитесь. Продолжим работу.

-Давайте теперь вернемся к нашему паруснику. Сможем ли мы теперь вычислить площадь паруса, а затем и площадь всего парусника? /Сможем/

-Что необходимо сделать?

/Нужно провести высоту к известной стороне и вычислить по формуле. А затем сложить все найденные площади. (Проводят вычисления)/

1. Самостоятельная работа по вариантам с самопроверкой (6 минут)

Время ограничено. Думаем быстро. Готовы?

Источник: nsportal.ru

Конспект урока по математике «Площадь треугольника», 4 класс

Урок математики в 4 классе. Тема: Площадь треугольника. Плоскостное моделирование и конструирование. аппликация из геометрических фигур — треугольников

Цели:

– вывести формулу нахождения площади прямоугольного треугольника;

– закрепить представления учащихся о разных видах треугольников (по углам, по сторонам);

– развивать наблюдательность, внимание, познавательные способности, логическое мышление, пространственное воображение;

– развивать умения и навыки конструирования, умение использовать геометрические термины, понятия;

– формировать художественно-творческую личность; творчески использовать жизненные наблюдения и собственную фантазию в процессе создания изображений;

– воспитывать коллективизм, взаимовыручку, любознательность.

Оборудование: конверты с представленными геометрическими фигурами, наборы цветной бумаги и картона, ножницы, клей, чертёжные инструменты, палетка.

Ход занятия

I. Организационный момент. Проверка готовности учащихся к уроку. Психологический настрой класса.

II. Интеллектуальная разминка.

Учитель. На уроке вам необходимо будет работать в группах. Но для того чтобы групповая работа была эффективной, каждый в отдельности должен уметь проявить себя.

— Разгадайте кроссворд и постарайтесь определить тему урока.

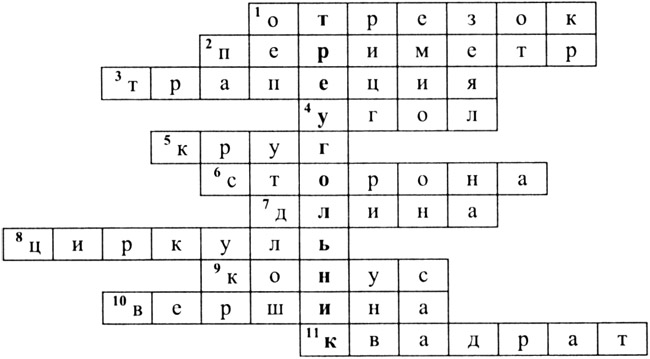
1. Если две точки соединить прямой линией, то получится. (отрезок).

2. Как называется сумма длин сторон многоугольника? (Периметр.)

3. От треугольника вершину

Вмиг отрезав ножницами,

Увидим новую фигуру

И назовём её. (трапеция).

4. Что получится, если из одной точки провести два луча? (Угол.)

5. Какую геометрическую фигуру ограничивает окружность? (Круг.)

6. От вершины по лучу,

Словно с горки, покачу.

Только луч теперь — «она»

И зовется. («сторона»).

7. Как называется большая сторона прямоугольника? (Длина.)

8. Сговорились две ноги

Делать дуги и круги. (Циркуль.)

9. Это — колпачок клоуна.

Я воронка, закрытая крышкой.

10. Как называется точка, из которой выходят два луча и образуют угол? (Вершина.)

11. Не овал я и не круг,

Треугольнику не друг.

Прямоугольнику я брат,

А зовут меня. (квадрат).

— Прочитайте по выделенным буквам название фигуры, представление о которой мы сегодня будем углублять.

III. Развитие психических механизмов.

— Что отличает треугольники от других фигур?

Варианты заданий для групп

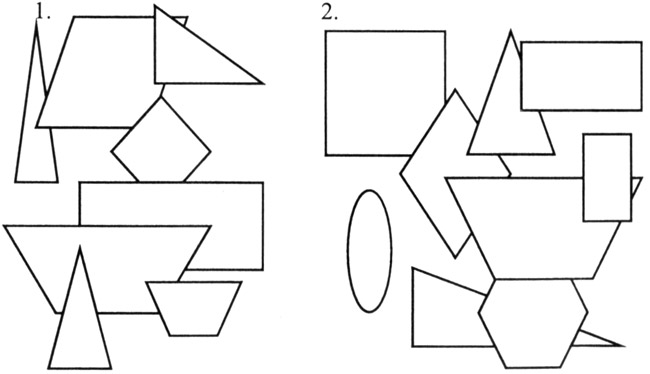
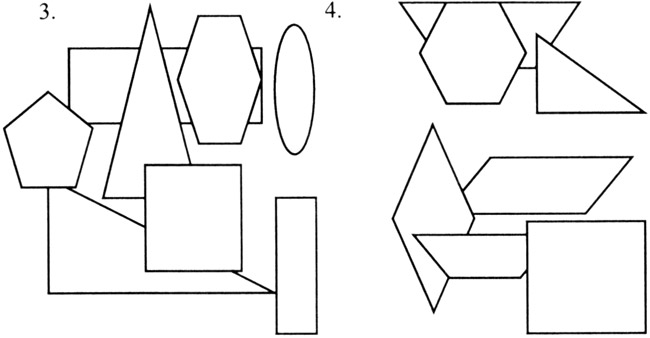
IV. Решение частично-поисковых задач разного уровня.

— Какой треугольник «лишний» и почему?

I группа: №3 — тупоугольный треугольник, остальные — прямоугольные.

II группа: №2 — разносторонний треугольник, остальные — равнобедренные.

III группа: № 4 — прямоугольный треугольник, остальные — остроугольные.

IV группа: №1 — равносторонний треугольник, остальные — равнобедренные.

— На какие группы мы можем разбить треугольники?

Физкультминутка

(отрывок из стихотворения)

Треугольник с Квадратом.

Старший был квадратный,

Добродушный и приятный.

Стал расспрашивать Квадрат:

«Почему ты злишься, брат?»

Тот кричит ему: «Смотри,

Ты полней меня и шире;

У меня углов лишь три,

У тебя же все четыре».

Но квадрат ответил: «Брат,

Я же старше, я — квадрат».

И сказал ещё нежней:

«Неизвестно, кто нужней!»

Но настала ночь, и к брату,

Натыкаясь на столы,

Младший лезет воровато

Срезать старшему углы.

Уходя, сказал: «Приятных

Я тебе желаю снов!

Спать ложился ты квадратным,

А проснёшься без углов!»

Дети инсценируют стихотворение.

— Какими фигурами являются отрезанные у квадрата углы? (Прямоугольными треугольниками.)

— Почему? (У квадрата все углы прямые.)

— Начертите на листке прямоугольный треугольник со сторонами 3 см и 4 см, образующими прямой угол.

— Найдите периметр этого прямоугольного треугольника. (Р = 3 см + 4 см + 5 см = 12 см.)

— А теперь найдите площадь. Как можно найти площадь данного треугольника? (Используя палетку.)

— Достройте данный треугольник до прямоугольника. Подумайте над тем, как еще, более простым способом, найти площадь прямоугольного треугольника. (Предположения детей.)

— Как проверить, что данные треугольники равны? (Наложением фигур.)

Вывод: чтобы найти площадь прямоугольного треугольника, нужно перемножить катеты и полученный результат разделить на 2.

V. Решение творческих задач.

— Составьте фигуру-силуэт «Танграм».

— Я предлагаю вам надеть «волшебные очки», через которые мы будем видеть наш мир треугольным.

— Вам поручили проиллюстрировать русскую народную сказку «Колобок». Подумайте, какими должны быть сказочные герои.

Итак, желаю вам удачи.

VI. Итог урока.

— Представляем свои работы.

Организуется выставка поделок.

— Замечательные работы. Молодцы!

Домашнее задание.

1. Дома поиграть в игру «Давай пофантазируем». (Желающие могут взять домой листок, на котором изображены пять треугольников, и дорисовать их, объединив одной темой или картиной.)

2. Сочинить свою сказку или историю по полученной картинке.

Источник: kladraz.ru

1. Площадь прямоугольного треугольника

Прямоугольный треугольник можно достроить до прямоугольника. Площадь этого прямоугольника будет в два раза больше площади треугольника.

Как найти площадь прямоугольного треугольника?
Известно, что площадь прямоугольника равна произведению длин его сторон:
S пр = a ⋅ b .

Поэтому для определения площади прямоугольного треугольника необходимо это произведение a ⋅ b разделить на (2).

Чтобы найти площадь прямоугольного треугольника, нужно произведение его катетов разделить на (2).
S = ( a ⋅ b ) : 2

найти площадь прямоугольного треугольника, если его катеты равны (10) см и (15) см .
S = ( a ⋅ b ) : 2 ;
S = ( 10 ⋅ 15 ) : 2 = 75 см 2 .
Ответ: 75 см 2 .

Если треугольник не имеет прямого угла, то можно разделить его на два прямоугольных треугольника, как показано на рисунке. Площадь треугольника будет равна сумме площадей двух полученных прямоугольных треугольников.

Площадь фигуры равна сумме площадей её частей.

Заметим, что если нужно найти площадь части фигуры, то можно из площади всей фигуры вычесть площадь другой его части.

Источник: www.yaklass.ru