Пид регулятор программа код

Содержание

Эту тему я решил выложить, потому, что долго искал простое описание и практическую реализацию ПИД регулятора. Толкового описания для “чайников” я так и не нашел, а практическая реализация сводится либо к использованию библиотек, либо сравнима с запуском ракеты на луну. Про подбор коэффициентов для регулятора вообще скромно умолчу, потому что это сродни танцам с бубном. Причем в каждом конкретном случае и недай бог изменятся какие-то начальные условия…

Выношу на ваш суд своё видение и реализацию ПИД регулятора. Может я и изобрел влосипед… Но если все попробуют и протестируют предложенный тип регулятора, а потом выскажут свое мнение, будет очень интересно. Возможно это облегчит кому-нибудь жизнь.

Алгоритм работы ПИД регулятора.

Теория:

Работа регулятора основана на пропорциональном регулировании, которое зависит от разности заданной и реальной величины регулирования и скорости нарастания реальной величины.

Предлагаемый регулятор имеет следующие особенности и характеристики;

Уроки Ардуино. ПИД регулятор

Высокая скорость нарастания выхода мощности регулирования при большой разнице между заданной величиной и измеренной.
Высокая точность и плавность изменения мощности при небольшой разнице между заданной величиной и измеренной.
Стабильность работы на всех краях диапазона регулирования.
Простота математического расчёта.
Малая зависимость от способа и типа прикладываемой мощности и количества или обьема регулируемого тела.

Можно представить, что величиной регулирования управляет оператор, который основывается только на показаниях измеряемой величины. Например: необходим нагрев тела неизвестной массы нагревательным элементом неизвестной мощности. Из величин, мы имеем измеренную, текущую температуру нагреваемой массы и заданную температуру.

Мощность нагревательного элемента оператор может регулировать или включать и выключать по своему усмотрению. Если реальная температура ниже заданной, то оператор будет постепенно добавлять мощность нагрева следя за показаниями реальной температуры.

Если разность заданной и реальной температур будет оставаться относительно большой, а скорость нарастания температуры маленькой или не меняться, то оператор постепенно доведет мощность нагрева до максимума. После начала повышения температуры, оператор начнет экстраполировать скорость нарастания температуры, чтобы вовремя уменьшить мощность нагрева, так чтобы при существующей скорости нарастания температуры, реальная температура была-бы близка к заданной. Таким образом наступит баланс между мощностью нагревательного элемента и реальной температурой, которая будет стремиться к заданной. Чем точнее будут измерения реальной температуры и чем чаще оператор будет производить экстраполяцию и регулирование мощьности нагревателя, тем точнее будет поддерживаться заданная температура. Из за того, что в реальности скорость нарастания температуры всегда разная, то частота экстраполирования и регулирования мощности подбирается соответственно такой, что-бы получить приемлемое приближение к заданной температуры и минимальное ее изменение по величине (синусойда).

В классическом ПИД регуляторе применяются три вычисляемых коэффициента, не считая временных переменных. Это П – пропорциональная составляющая, И – интегральная составляющая, Д – интегральная составляющая.

В предлагаемом регуляторе применяются два вычисляемых коэффициента. П – пропорциональная составляющая указывающая на разность заданной и реальной величины регулирования, И — интегральная составляющая указывающая на скорость изменения реальной величины. П – дает приращение величины регулирования. И – ограничивает приращение величины регулирования.

Практическое описание:

Рассмотрим классический пример регулировании температуры от 0 до 100* при регулировании прилагаемой мощности от 0 до 100% с временем интегррования 1сек. При регулировании неважно количество, масса, теплоемкость и тепло потери нагреваемого тела, а также прилагаемая мощность нагрева. Главное условие, что при прилагаемой мощности нагрева равной 100% , нагрев нагреваемого обьекта достигает или превышает заданное значение температуры, а при прилагаемой мощьности равной 0% происходит остывание обьекта.

При начальных условия температура нагреваемого объекта относительно мала, а заданная температура относительно высокая. Поэтому пропорциональная составляющая — П будет высокой. П = (Т.заданная-Т.реальная)*П.коэффицент

Приращение температуры – И, сначала будет небольшое и будет проверяться с начала времени интервала интегррования и по окончании. В нашем случае время интегрирования принято 1 сек. И = (Т.нач.интегр. — Т.кон.интегр.)*И.коэффициент

Выходная мощность Р.вых будет рассчитываться через каждый интервал времени интегррования, в нашем случае это 1 сек. Она будет равна приращению пропорциональной составляющей – П и вычитанию интегральной составляющей – И.

Полная формула расчета будет выглядеть следующим образом:

Р.вых = Р.вых + П – И

Р.вых = Р.вых + (Т.зад-Т.реал)*П.коэф – (Т.нач.интегр. — Т.кон.интегр.)*И.коэф

Вычисления будут проводиться каждый интервал времени интегрирования, в нашем случае это 1 сек.

При превышении выходной мощности Р.вых установленного максимального значения, оно приравнивается максимальному значению (при Р.вых > 100 тогда Р.вых = 100). При уменьшении выходной мощности Р.вых меньше минимального значения, оно приравнивается минимальному значению (при Р.вых < 0 тогда Р.вых = 0). Таким образом ограничивается минимальная и максимальная мощность.

При приближении реальной температуры к заданной, коэффициенты П и И будут стремится к нулю и изменяться только при нарушении реальной и заданной температуры. Поэтому после достижения реальной температуры и заданной, регулятор останется в покое, пока разница температур не изменит коэффициенты в формуле расчёта. Причем если интегральная составляющая будет отрицательной, тоесть температура будет падать, то минус в формуле будет давть плюс и интегральная составляющая уже будет не ограничивать, а увеличивать приращение выхода регулятора, тем самым увеличивая скорость реагирования. При повышении реальной температуры над заданной, коэффициент П уже будет с отрицательным значением и уменьшать величину выхода. Коэффициент И в этом случае тоже поменяет значение с минуса на плюс и будет ограничивать скорость уменьшения выхода регулятора.

Таким образом скорость нарастания выходной мощности будет варьироваться пропорциональной составляющей – П и ограничиваться интегральной составляющей – И и вписываться в установленные рамки минимальной и максимальной мощности. Расчёт текущей мощности будет верен в пределах установленного интервала времени, в нашем случае это 1 сек.

Математика работы этого регулятора тоже очень простая, и позволяет легко регулировать мощность в указанных пределах и необходимой скоростью. Также регулятор легко позволяет динамически менять диапазон пределов и скорость регулирования прямо в процессе работы.

Предварительные испытания с различными мощностями нагрева и разными объёмами нагреваемого тела, показали, что регулятор настраивается один раз. Коэффициенты были взяты следующим образом П.коэф – 0,21 И.коэф – 2,9 . Коэффициенты были выбраны таким образом, чтобы обеспечить приемлемую скорость нарастания при относительно большой разнице между реальной и заданной температурой, а также примерно одинаковую компенсацию параметров «П» и «И» в диапазоне примерно равных значений между реальной и заданной температурой. Регулятор уверенно регулирует нагрев, независимо от объёма нагреваемого тела и при различных мощностях нагревательных элементов. Также для настроенного регулятора нет разницы, какой тип мощности прикладывается для организации нагрева. Это может быть 1- аналоговый тип мощности, 2- широтно импульсный тип мощности, 3- дискретно импульсный тип мощности.

При дискретном регулировании мощности, регулятор показал высокую стабильность, точность и скорость регулирования температуры нагреваемого тела. Был применен следующий метод дискретным регулированием нагрева. Общий интервал сигнала был выбран равным 10 сек.

ПИД-регулятор

После добавления интегральной составляющей, картинка станет такой:

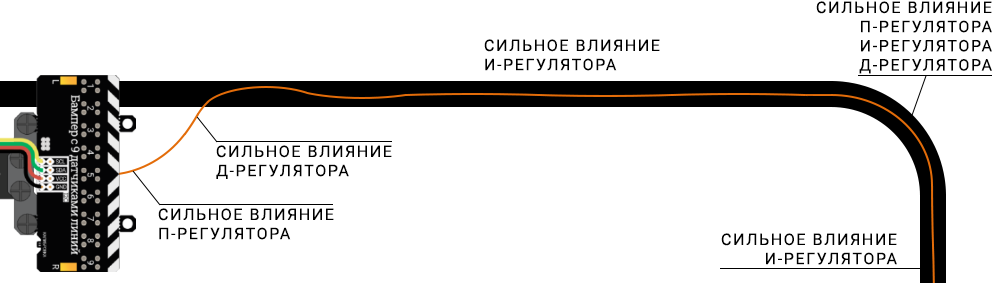
И-регулятор накапливает ошибки и оценивает их сумму. Это позволяет ему справляться со статическими или слабыми ошибками. Теперь машина едет по прямой и на повороте ровнее

Код ПИД-регулятора:

float ERR[10] = ; // Определяем массив последних ошибок // void loop()< // i++; if( i>=10 ) < i=0; >// Переходим к следующему элементу массива «ERR» ERR[i] = bum.getErrPID(); // Получаем текущую ошибку SUM = 0; for( auto a:ERR ) < SUM+=a; >// Получаем сумму последних ошибок P = ERR[i] * kP; // Определяем пропорциональную составляющую регулятора I = SUM * kI; // Определяем интегральную составляющую регулятора D = ( ERR[i]-ERR[j] ) * kD; // Определяем дифференциальную составляющую регулятора PID = P + I + D; // Получаем результат ПИД-регулятора j = i; // Сохраняем номер элемента массива «ERR» в котором хранится текущая ошибка, > // на следующем проходе цикла она станет предыдущей ошибкой

До цикла определяем массив ERR для хранения 10 последних ошибок;
Предполагается, что остальные переменные кода также объявлены;
Первая строка цикла увеличивает значение i на 1, со сбросом в 0 при достижении 10;
Вторая строка сохраняет текущую ошибку в элемент ERR[i];
Третьей строкой мы получаем в переменную SUM сумму последних 10 ошибок;
Следующие три строки определяют составляющие ПИД регулятора;
Предпоследняя строка получает результат PID как сумму составляющих P + I + D;
Последней строкой значение i сохраняется в j . Значит, при каждом новом проходе цикла элемент ERR[i] хранит текущую ошибку, а ERR[j] хранит предыдущую ошибку.

Настройка ПИД-регулятора:

Настройка ПИД-регулятора сводится к поиску коэффициентов для пропорциональной, интегральной и дифференциальной составляющих.
Сброс любого из коэффициентов в 0 приводит к отключению его составляющей:

Спрос kP в ПИД-регуляторе приведёт к получению ИД-регулятора;
Спрос kI в ПИД-регуляторе приведёт к получению ПД-регулятора;
Спрос kD в ПИД-регуляторе приведёт к получению ПИ-регулятора.

Слишком высокий kD приведёт к тому, что машина начнёт «дрожать» на прямой линии;
Слишком низкий kD не избавит от «виляний» машины на прямых участках и не улучшит прохождение крутых поворотов;
Оптимальным является kD, при котором бампер машины не покидает линию на всех поворотах трассы. При этом машина не «виляет» и не «дрожит» на прямых участках;
После настройки kD можно снизить kP, если это не ухудшит движение машины;

Слишком высокий kI похож на перерегулировку kP — машина начнёт «вилять»;
В процессе настройки kI можно снизить подобранные ранее kP и kD.

Коэффициент регулятора определяет силу воздействия регулятора.

Чем больше коэффициент, тем сильнее меняется выходная величина.

Обычно kD >kP, так как разность ошибок меньше одной ошибки, значит, коэффициент больше.
Обычно kI< kP, так как сумма ошибок больше одной ошибки, значит, коэффициент меньше.

Скетч для одной скорости:

Скорость колёс в скетче задаётся функцией setSpeed () в процентах.
Выберем скорость машины, равную 60%. Именно эту скорость мы и указываем обоим колёсам.
Предположим, что при kI = 0, kD = 0, kP = 8 машина не покидает повороты трассы.
Предположим, что при kI = 0, kD = 14.4, kP = 8 машина перестала «вилять» на прямых участках.
Предположим, что при kI = 0.1, kD = 14.4, kP = 8 бампер не покидает центр линии на поворотах.

#include // Подключаем библиотеку для работы с аппаратной шиной I2C #include // Подключаем библиотеку для работы с мотором I2C-flash #include // Подключаем библиотеку для работы с бампером I2C-flash // iarduino_I2C_Motor mot_R (0x0A); // Объявляем объект mot_R для правого мотора, указав адрес модуля на шине I2C iarduino_I2C_Motor mot_L (0x0B); // Объявляем объект mot_L для правого мотора, указав адрес модуля на шине I2C iarduino_I2C_Bumper bum(0x0C); // Объявляем объект bum для работы с бампером I2C-flash, указав адрес модуля на шине I2C // float speed = 60; // Скорость машины в % float kP = 8; // Коэффициент пропорциональной составляющей float kI = 0.1; // Коэффициент интегральной составляющей float kD = 14.4; // Коэффициент дифференциальной составляющей float ERR[10] = ; // Определяем массив последних ошибок uint8_t i; // Объявляем переменную указывающую на элемент массива «ERR» хранящий текущую ошибку // void setup() < // mot_R.begin(); // Инициируем работу с левым мотором I2C-flash mot_L.begin(); // Инициируем работу с правым мотором I2C-flash bum.begin(); // Инициируем работу с бампером I2C-flash mot_R.setDirection(true); // Указываем правому мотору, что его вращение должно быть прямым (по часовой стрелке при положительных скоростях) mot_L.setDirection(false); // Указываем левому мотору, что его вращение должно быть обратным (против часовой стрелки при положительных скоростях) >// // void loop()< // i++; if( i>=10 ) < i=0; >// Переходим к следующему элементу массива «ERR» ERR[i] = bum.getErrPID(); // Получаем текущую ошибку float SUM = 0; for(auto j:ERR) // Получаем сумму последних ошибок float P = ERR[i] * kP; // Определяем пропорциональную составляющую регулятора float I = SUM * kI; // Определяем интегральную составляющую регулятора float D = (ERR[i]-ERR[(i+9)%10]) * kD; // Определяем дифференциальную составляющую регулятора float PID = P + I + D; // Получаем результат ПИД-регулятора mot_R.setSpeed( speed — PID, MOT_PWM ); // Устанавливаем скорость правого мотора mot_L.setSpeed( speed + PID, MOT_PWM ); // Устанавливаем скорость левого мотора >

Скетч для диапазона скоростей:

В предыдущем скетче все коэффициенты были найдены для скорости 60%. Если уменьшить скорость движения машины speed с 60% до 30%, то найденные ранее коэффициенты будут слишком велики, и мы получим перерегулирование.

Выход из положения — найти коэффициенты для минимальной и максимальной скоростей машины, после чего вывести формулы зависимости коэффициентов от скорости. Мы уже так делали в предыдущих уроках с коэффициентами kP и kD. Коэффициент kI обычно столь мал, что не сильно зависит от скорости.

Теперь можно написать скетч, у которого скорость можно менять от 20 до 60%:

#include // Подключаем библиотеку для работы с аппаратной шиной I2C #include // Подключаем библиотеку для работы с мотором I2C-flash #include // Подключаем библиотеку для работы с бампером I2C-flash // iarduino_I2C_Motor mot_R (0x0A); // Объявляем объект mot_R для правого мотора, указав адрес модуля на шине I2C iarduino_I2C_Motor mot_L (0x0B); // Объявляем объект mot_L для правого мотора, указав адрес модуля на шине I2C iarduino_I2C_Bumper bum(0x0C); // Объявляем объект bum для работы с бампером I2C-flash, указав адрес модуля на шине I2C // float speed = 60; // Скорость машины в %. float kP = 3 + 0.125*(speed-20); // Коэффициент пропорциональной составляющей float kI = 0.1; // Коэффициент интегральной составляющей float kD = speed*speed/250; // Коэффициент дифференциальной составляющей float ERR[10] = ; // Определяем массив последних ошибок uint8_t i; // Объявляем переменную, указывающую на элемент массива «ERR», который хранит текущую ошибку // void setup() < // mot_R.begin(); // Инициируем работу с левым мотором I2C-flash mot_L.begin(); // Инициируем работу с правым мотором I2C-flash bum.begin(); // Инициируем работу с бампером I2C-flash mot_R.setDirection(true); // Указываем правому мотору, что его вращение должно быть прямым (по часовой стрелке при положительных скоростях) mot_L.setDirection(false); // Указываем левому мотору, что его вращение должно быть обратным (против часовой стрелки при положительных скоростях) >// // void loop()< // i++; if( i>=10 ) < i=0; >// Переходим к следующему элементу массива «ERR» ERR[i] = bum.getErrPID(); // Получаем текущую ошибку float SUM = 0; for(auto j:ERR) // Получаем сумму последних ошибок float P = ERR[i] * kP; // Определяем пропорциональную составляющую регулятора float I = SUM * kI; // Определяем интегральную составляющую регулятора float D = (ERR[i]-ERR[(i+9)%10]) * kD; // Определяем дифференциальную составляющую регулятора float PID = P + I + D; // Получаем результат ПИД-регулятора mot_R.setSpeed( speed — PID, MOT_PWM ); // Устанавливаем скорость правого мотора mot_L.setSpeed( speed + PID, MOT_PWM ); // Устанавливаем скорость левого мотора >

Этот скетч отличается от предыдущего только тем, что значения kP и kD определены не числами, а формулами.

При изменении значений скорости speed в пределах от 20% до 60%, будут автоматически пересчитываться коэффициенты kP и kD, и машина продолжит корректно двигаться по линии

Итак, мы получили ПИД-регулятор — зачастую самый оптимальный способ регулирования. При грамотной настройке можно добиться невероятно точной и в то же время быстрой езды. Обязательно «поиграйтесь» с коэффициентами, если Вы этого еще не делали.

Недостаток ПИД-регулятора:

ПИД-регулятор настраивается дольше, чем П-регулятор или ПД-регулятор, так как нужно подобрать все три коэффициента;
ПД-регулятор позволяет развивать более высокую скорость, чем ПИД-регулятор.

Источник: robotraffik.ru

ПИД регулятор

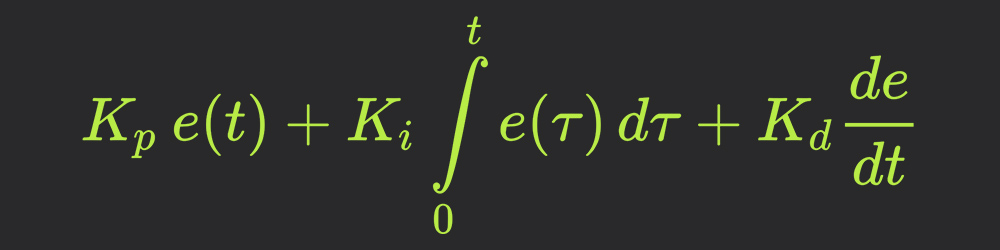
ПИД регулятор – один из самых распространенных автоматических регуляторов. Он настолько универсален, что применяется практически везде, где нужно автоматическое управление. Например температурой: специальные печи, холодильники, инкубаторы, паяльники, сопло и стол 3D принтера, ИК паяльные станции и прочее. Поддержание частоты оборотов мотора, например для станков.

Всевозможные балансирующие штуки, гироскутеры, сигвеи, левитирующие магнитные платформы, и конечно же квадрокоптеры и самолёты с автопилотом. Это всё ПИД регулятор. Почему именно ПИД? Существуют и другие регуляторы, превосходящие ПИД по адаптивности к управляемой системе и стабильности, например линейно квадратичный. Но, чтобы грамотно синтезировать такой регулятор, нужно быть гораздо больше чем “семи пядей” во лбу, а настройка ПИД регулятора дело хоть и неприятное, но фактически очень простое и под силу любому, а сам ПИД регулятор универсален для почти любого процесса.

Система управления

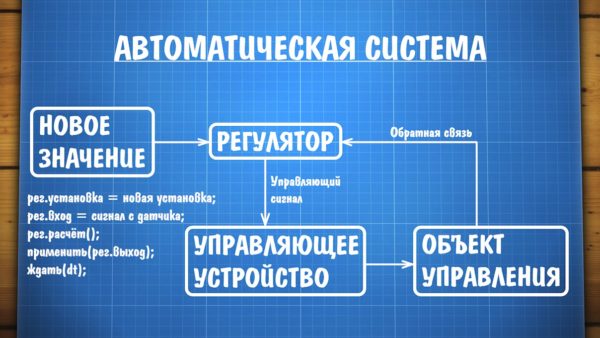
blank

Прежде чем переходить непосредственно к пиду, очень важно понять и запомнить несколько базовых понятий, из которых состоит автоматическая система. В первую очередь это регулятор, который всем заправляет и находится в центре системы. Регулятор в данном понимании – математический алгоритм или часть программы, которая крутится на микроконтроллере.

Регулятор, как алгоритм, работает с обычными числами. Объект управления – это девайс, которым мы управляем, например печка или мотор. Для этого у нас есть управляющее устройство, например диммируемый тен или драйвер мотора. Управляющее устройство получает от регулятора управляющий сигнал, то есть конкретное число.

Это может быть заполнение шим сигнала, от 0 до 255, а может быть угол поворота сервомашинки от 0 до 180, потому что регулятору без разницы чем управлять. В объекте управления у нас стоит датчик, с которого регулятор получает управляемую величину, то есть текущий сигнал с датчика. Это – обратная связь, которая и даёт возможность системе ирчно поддержать заданное значение.

В случае с печкой это температура, а с мотором – частота оборотов. Ну и наконец регулятор получает установку (уставку), то есть число, к которому он должен привести текущее значение с датчика. Установка может задаваться каким угодно образом: крутилкой, ползунком, энкодером, кнопками, да хоть смской или голосовым вводом. Регулятору это неважно, для него это просто цифра.

Задача регулятора состоит в том, чтобы сравнивать текущее значение с установкой и выдавать управляющий сигнал на управляющее устройство. То есть в программе это будет выглядеть условно так: регулятор получил установку, регулятор получил значение с датчика, регулятор выполнил вычисления и выдал нам управляющий сигнал, опять же число. Если это шим – мы его подаём через функцию генерации шим. Есть ещё один момент – регулятор должен делать расчёты и применять управляющий сигнал через равные промежутки времени, то есть с равным периодом или частотой. Эта частота называется частотой дискретизации системы, а период обозначается как dt, прямо как период интегрирования.

Под капотом у ПИД регулятора

ПИД регулятор состоит из трёх составляющих: пропорциональной P, интегрирующей I и дифференциирующей D, формируется просто как сумма трёх значений, умноженных каждая на свой коэффициент. Эта сумма после вычислений становится управляющим сигналом, который подаётся на управляющее устройство, обозначим его как out.

out = P*kP + I*kI + D*kD

kP, kI и kD это и есть те самые коэффициенты, которые нужно настроить для работы ПИДа. Значения тут могут быть самые разные, от 0.001 то десятков и тысяч, это зависит от конкретной системы. Тут есть ещё один момент: любой коэффициент может быть равен нулю, и в таком случае обнуляется вся его компонента.

P составляющая

Пропорциональная составляющая предоставляет собой разность текущего значения с датчика и установки.

P = setpoint — input

Данная разность называется ошибкой регулирования, то есть насколько далеко находится система от заданного значения. Получается чем больше ошибка, тем больше будет управляющий сигнал и тем быстрее система будет приводить управляемую величину к заданному значению. Коэффициент kP тут влияет роль усиления ошибки и настраивается вручную.

Но в то же время, если система пришла к заданной величине, ошибка станет равной нулю, и управляющий сигнал тоже! Другими словами, п регулятор никогда не сможет привести к заданному значению, всегда будет некая ошибка. П составляющая является основной в ПИД регуляторе и так сказать тянет самую большую лямку, регулятор может неплохо работать только лишь на ней одной. P составляющая исправляет ошибку в текущий момент времени.

I составляющая

Интегральная составляющая просто суммирует в саму себя ту же самую ошибку, разность текущего и заданного значения, умноженную на период дискретизации системы, то есть на время, прошедшее с предыдущего расчёта dt – фактически берёт интеграл от ошибки по времени.

I = I + (setpoint — input) * dt

В самом регуляторе это ещё умножается на коэффициент kI, которым настраивается резкость данной составляющей. В интегральной составляющей буквально копится ошибка, что позволяет регулятору с течением времени полностью её устранить, то есть привести систему ровно к заданному значению с максимальной точностью. I составляющая исправляет прошлые, накопившиеся ошибки.

D составляющая

Дифференциальная составляющая представляет собой разность текущей и предыдущей ошибки, поделенную на время между измерениями, то есть на ту же dt, которая общий период регулятора. Иными словами – это производная от ошибки по времени.

err = setpoint — input D = (err — prevErr) / dt prevErr = err

Фактически D составляющая реагирует на изменение сигнала с датчика, и чем сильнее происходит это изменение, тем большее значение прибавляется к общей сумме. Иными словами, D позволяет компенсировать резкие изменения в системе и при правильной настройке предотвратить сильное перерегулирование и уменьшить раскачку.

Коэффициент д позволяет настроить вес, или резкость данной компенсации, как и остальные коэффициенты регулируют свои составляющие. D составляющая в первую очередь нужна для быстрых систем, то есть для систем с резкими изменениями, такие как квадрокоптер или шпиндель станка под переменной нагрузкой. D составляющая исправляет возможные будущие ошибки, анализируя скорость.

Настройка регулятора

Для настройки регулятора нужно варьировать коэффициенты:

При увеличении kP увеличивается скорость выхода на установленное значение, увеличивается управляющий сигнал. Чисто математически система не может прийти ровно к заданному значению, так как при приближении к установке П составляющая пропорционально уменьшается. При дальнейшем увеличении kP реальная система теряет устойчивость и начинаются колебания.
При увеличении kI растёт скорость компенсации накопившейся ошибки, что позволяет вывести систему точно к заданному значению с течением времени. Если система медленная, а kI слишком большой – интегральная сумма сильно вырастет и произойдёт перерегулирование, которое может иметь характер незатухающих колебаний с большим периодом. Поэтому интегральную сумму в алгоритме регулятора часто ограничивают, чтобы она не могла увеличиваться и уменьшаться до бесконечности.
При увеличении kD растёт стабильность системы, она не даёт системе меняться слишком быстро. В то же время kD может стать причиной неадекватного поведения системы и постоянных скачков управляющего сигнала, если значение с датчика шумит. На каждое резкое изменение сигнала с датчика Д составляющая будет реагировать изменением управляющего сигнала, поэтому сигнал с датчика нужно фильтровать (читай урок по фильтрам).

Вот так выглядит процесс стабилизации при изменении коэффициентов: Настройка регулятора – дело не очень простое. Начальные коэффициенты для подбора можно получить по следующему алгоритму: сначала выставляем все коэффициенты в 0. Плавно увеличиваем kP до появления незатухающих колебаний. Значение kP, при котором они появились, запишем и обозначим как kP1. Далее замеряем период колебаний системы в секундах, обозначим как T. Итоговые коэффициенты получим так:

kP = 0.6 * kP1
kI = kP / T * 2 * dt
kD = kP * T / 8 / dt

Например, незатухающие колебания появились при kP 20, период колебаний составил 3 секунды. Период dt в системе будет 50 мс (0.05 с). Считаем:

kP: 0.6*20=12
kI: 12/3*2*0.05=0.4
kD: 12*2/8/0.05=60

На полученных коэффициентах должны более-менее работать большинство систем, но не все. Также можно воспользоваться автоматическим тюнером коэффициентов, например два разных алгоритма встроены в библиотеку GyverPID.

Реализация на C++

Соединяя все рассмотренные выше уравнения, получим:

// (вход, установка, п, и, д, период в секундах, мин.выход, макс. выход) int computePID(float input, float setpoint, float kp, float ki, float kd, float dt, int minOut, int maxOut) < float err = setpoint — input; static float integral = 0, prevErr = 0; integral = constrain(integral + (float)err * dt * ki, minOut, maxOut); float D = (err — prevErr) / dt; prevErr = err; return constrain(err * kp + integral + D * kd, minOut, maxOut); >

Это готовая функция, которая принимает значение с датчика, установку, три коэффициента и время, а также ограничение выхода с регулятора.

Как пользоваться этой функцией: функция должна вызываться с некоторым периодом, причем длительность этого периода нужно будет передать в функцию в секундах. Если попроще, можно использовать задержку. Но делать так не рекомендуется, лучше сделать таймер на миллис и работать с ним. Функция возвращает управляющий сигнал, то есть можно подать его например как ШИМ.

Период dt имеет такой смысл: чем инерционнее у нас система, тем реже можно вычислять пид. Например для обогрева комнаты период можно поставить 1 секунду или больше, а для контроля за оборотами двигателя надо будет поставить пару десятков миллисекунд, то есть около сотни раз в секунду.

Библиотеки

GyverPID – моя библиотека со встроенным тюнером коэффициентов
QuickPID – хорошая библиотека с интересными возможностями (оптимизация интегральной суммы, смешанный режим пропорционально ошибке/измерению)
sTune – тюнер коэффициентов, несколько алгоритмов

Видео

Полезные страницы

Набор GyverKIT – большой стартовый набор Arduino моей разработки, продаётся в России
Каталог ссылок на дешёвые Ардуины, датчики, модули и прочие железки с Aliexpress у проверенных продавцов
Подборка библиотек для Arduino, самых интересных и полезных, официальных и не очень
Полная документация по языку Ардуино, все встроенные функции и макросы, все доступные типы данных
Сборник полезных алгоритмов для написания скетчей: структура кода, таймеры, фильтры, парсинг данных
Видео уроки по программированию Arduino с канала “Заметки Ардуинщика” – одни из самых подробных в рунете
Поддержать автора за работу над уроками
Обратная связь – сообщить об ошибке в уроке или предложить дополнение по тексту ([email protected])

Источник: alexgyver.ru

ПИД-регулятор

Код ПИД-регулятора:

Настройка ПИД-регулятора:

Скетч для одной скорости:

Скетч для диапазона скоростей:

Недостаток ПИД-регулятора:

ПИД регулятор

Система управления

Под капотом у ПИД регулятора

P составляющая

I составляющая

D составляющая

Настройка регулятора

Реализация на C++

Библиотеки

Видео

Полезные страницы

Составьте блок схему и программу вычисления значения функции вариант 3

Напиши программу которая в последовательности натуральных чисел определяет количество чисел кратных

Как записать музыку на сд диск в формате сд программа

Какая нужна программа на телефон чтобы скачивать музыку на телефон

Если не хватает места на диске с для установки программы

Как расширение имени файла связано с форматом файла и программой обработки

Что программа 12111 переводит число 50 в число 20 определите значение b

Задачи по ознакомлению с формой и геометрическими фигурами в программе радуга