Параметрическое программирование
Общая задача линейного программирования содержит постоянные величины: коэффициенты , и свободные члены . С одной стороны, при определении этих величин на практике встречаются с тем, что в действительности они не являются постоянными, а их значения изменяются в некоторых интервалах; с другой, найдя оптимальный план некоторой экономической задачи при фиксированных значениях ,, , полученных из опыта, необходимо знать, в каких допустимых пределах можно их изменять, чтобы план оставался оптимальным.
Поэтому возникает необходимость исследовать поведение оптимального решения задачи линейного программирования при изменении ее коэффициентов и свободных членов. Исследования подобного рода составляют предмет параметрического линейного программирования. Параметрическое программирование возникло в связи с изучением задач планирования производства и дает возможность управлять оптимальным планированием различных экономических процессов, которые могут быть описаны линейной математической моделью.
Параметрическая мебель за пару минут в 3d max и rayfire | Урок 3Ds MAX #5.15
Задача с параметром в целевой функции



Предположим, что коэффициенты линейной функции могут изменяться в некоторых допустимых пределах , тогда для удобства исследования коэффициенты линейной функции можно заменить выражением , где — постоянные, а t — параметр, изменяющийся в некоторых пределах. В этом случае математическая задача может быть поставлена следующим образом.

Дана линейная функция

и система линейных ограничений

Считая значение параметра равным некоторому числу , находим симплексным методом или методом искусственного базиса решение, полученной таким образом задачи линейного программирования.

В результате при данном значении либо найдем оптимальный план задачи, либо установим ее неразрешимость. В первом случае, используя элементы — й строки последней симплекс — таблицы решения задачи, в которой записаны числа , находим:

Для всех задача имеет один и тот же оптимальный план, что и при .






В том случае, если задача при неразрешима, — в строке последней симплекс — таблицы ее решения имеется число , где . Тогда:
1) если , то задача неразрешима для любого ;
2) если , то задача неразрешима для всех ;
3) если , то задача неразрешима для всех .
Определив все значения параметра , для которых задача имеет один и тот же оптимальный план или для которых задача неразрешима, получаем промежуток изменения параметра , который исключаем из рассмотрения. Снова полагаем значение параметра равным некоторому числу, принадлежащему промежутку, и находим решение полученной задачи.
После каждой итерации определяется либо промежуток, в котором для всех значений параметра задача имеет один и тот же оптимальный план, либо промежуток, в котором для всех значений параметра задача не имеет решения.
Процесс нахождения решения задачи включает следующие этапы:
1. Считая значение параметра равным некоторому числу , находят оптимальный план или устанавливают неразрешимость полученной задачи линейного программирования.
2. Определяют множество значений параметра , для которых найденный оптимальный план является оптимальным или задача неразрешима. Эти значения параметра исключают из рассмотрения.
3. Полагают значения параметра равным некоторому числу, принадлежащему оставшейся части промежутка , и находят решение полученной задачи линейного программирования.
4. Определяют множество значений параметра , для которых новый оптимальный план остается оптимальным или задача неразрешима. Вычисления повторяют до тех пор, пока не будут исследованы все значения параметра .
Пример 3.1.1. Для всех значений параметра найти максимальное значение функции

Решение. Возьмем (число 0 выбрано произвольно) и найдем симплекс-методом оптимальный план.
Определим значения , при которых план, соответствующий таблице 3.1.3, останется оптимальным:

Следовательно, при задача имеет оптимальное решение: Возьмем . Тогда столбец — разрешающий. Переходим к новому опорному плану:
Этот план оптимален при условии:

Следовательно, при При имеем:
Этот план оптимален при условии: . Следовательно, при
2. Задача с параметром в свободных членах системы ограничений
Дана линейная функция и система линейных ограничений


Алгоритм решения задачи (3.2.1)-(3.2.2) подобен рассмотренному выше алгоритму решения задачи (3.1.1)-(3.1.2). Полагая значение параметра равным некоторому числу , находим решение полученной задачи линейного программирования. При данном значении параметра либо определяем оптимальный план задачи, либо установим ее неразрешимость. В первом случае найденный план является оптимальным для любого , где






и числа и определены компонентами оптимального плана и зависят от :
Если при задача (3.2.1) — (3.2.2) неразрешима, то либо целевая функция задачи (3.2.1) не ограничена на множестве планов, либо система уравнений (3.2.2) не имеет неотрицательных решений. В первом случае задача неразрешима для всех , а во втором случае определяем все значения параметра , для которых система уравнений (3.2.2) несовместна, и исключаем их из рассмотрения. После определения промежутка, в котором задача (3.2.1) — 3.2.2) имеет один и тот же оптимальный план или неразрешима, выбираем новое значение параметра , не принадлежащее найденному промежутку, и находим решение полученной задачи линейного программирования. При этом решение новой задачи ищем с помощью двойственного симплекс-метода. Продолжая итерационный процесс, после конечного числа шагов получаем решение задачи (3.2.1) — (3.2.2). Итак, процесс нахождения решения задачи (3.2.1) — (3.2.2) включает следующие основные этапы:
1. Считая значение параметра равным некоторому числу , находят оптимальный план или устанавливают неразрешимость полученной задачи линейного программирования.
2. Находят значения параметра , для которых задача (3.2.1) — (3.2.2) имеет один и тот же оптимальный план или неразрешима. Эти значения параметра исключают из рассмотрения.
3. Выбирают значения параметра из оставшейся части промежутка и устанавливают возможность определения нового оптимального плана. В случае существования оптимального плана находят его двойственным симплекс-методом..
4. Определяют множество значений параметра , для которых задача имеет один и тот же новый оптимальный план или неразрешима. Вычисления проводят до тех пор, пока не будут исследованы все значения параметра .
Пример 3.2.1. Для каждого значения параметра найти максимальное значение функции

Решение. Считая , находим решение:
Источник: studbooks.net
Параметрическое программирование
Одним из самых интересных и эффективных методов программирования обработки является параметрическое программирование. Удивительно, но большинство технологов-программистов хоть и слышали об этом методе, но совершенно не умеют его использовать. В этом уроке вы познакомитесь с теорией параметрического программирования и коснетесь основ макроязыка системы ЧПУ современного станка.
Оглавление
- Основы числового программного управления
- Автоматическое управление
- Особенности устройства и конструкции фрезерного станка с ЧПУ
- Функциональные составляющие (подсистемы) ЧПУ
- Языки для программирования обработки
- Процесс фрезерования
- Режущий инструмент
- Вспомогательный инструмент
- Основные определения и формулы
- Рекомендации по фрезерованию
- Прямоугольная система координат
- Написание простой управляющей программы
- Создание УП на персональном компьютере
- Передача управляющей программы на станок
- Проверка управляющей программы на станке
- Советы по технике безопасности при эксплуатации станков с ЧПУ
- Нулевая точка станка и направления перемещений
- Нулевая точка программы и рабочая система координат
- Компенсация длины инструмента
- Абсолютные и относительные координаты
- Комментарии в УП и карта наладки
- G- и М-коды
- Структура программы
- Слово данных, адрес и число
- Модальные и немодальные коды
- Формат программы
- Строка безопасности
- Ускоренное перемещение – G00
- Линейная интерполяция – G01
- Круговая интерполяция – G02 и G03
- Введение
- Останов выполнения управляющей программы – М00 и М01
- Управление вращением шпинделя – М03, М04, М05
- Управление подачей СОЖ – М07, М08, М09
- Автоматическая смена инструмента – М06
- Завершение программы – М30 и М02
- Основные принципы
- Использование автоматической коррекции на радиус инструмента
- Активация, подвод и отвод
- Подпрограмма
- Работа с осью вращения (4-ой координатой)
- Параметрическое программирование
- Методы программирования
- Что такое CAD и САМ?
- Общая схема работы с CAD/САМ-системой
- Виды моделирования
- Уровни САМ-системы
- Геометрия и траектория
- Алгоритм работы в САМ-системе и постпроцессор
- Ассоциативность
- Пятикоординатное фрезерование и ЗD-коррекция
- Высокоскоростная (ВСО) и высокопроизводительная обработка
- Критерии для оценки, сравнения и выбора CAM-систем
Источник: www.planetacam.ru
Временные и параметрические программы управления
Одной из задач САУ является поддержание требуемого значения управляемой величины хВЬ1Х или ее программное изменение (программа может быть заранее задана или поступать во время работы в зависимости от определенных условий).
Программы управления могут задаваться как функции времени (временные):

или в определенных текущих координатах (параметрические):

где Si, S2, . Sn — какие-либо физические величины (параметры, координаты), характеризующие в процессе управления текущее состояние объекта регулирования.
На рис. 1.10 показаны примеры программ управления. Временная программа (рис. 1.10, а) обеспечивает правильный режим разгона мощного двигателя при его запуске до наступления режима нормальной эксплуатации. В этом случае хВЬ1Х — частота вращения двигателя, а автоматический регулятор частоты вращения предназначен не только для поддержания постоянной скорости хВЬ1Х.о (режим нормальной эксплуатации), но и для обеспечения заданного режима увеличения скорости во времени при запуске двигателя.

Рис. 1.10. Программы управления: а, б- временные программы; в — параметрическая программа
Если в некоторых процессах требуется обеспечить определенный режим скорости нагревания материала до нужной температуры хВЬ1Х.о, а затем выдержать его в печи, то подобная программа управления во времени может обеспечивать термическую обработку (на рис. 1.10, а, хВЬ1Х — температура в печи).
В отдельных случаях в процессе нормального режима работы объекта управления происходит непрерывное программное изменение управляемой величины во времени (рис. 1.10, б), например хВЬ1Х — угол тангажа на активном участке полета вертикально взлетающей ракеты.
Для обеспечения работы объекта по временной программе необходимо заложить ее в автоматический регулятор (систему управления), в котором имеется программное (задающее) устройство.
Пример параметрической программы регулирования показан на рис. 1.10, в, где хВЬ1Х — высота полета летательного аппарата, a S — пройденный путь. Такая программа позволяет снизиться в определенную точку координат независимо от времени снижения (посадка). Если в качестве хВЬ1Х возьмем давление, a S будет высотой, то получим программу управления переменным давлением в гермокабине летательного аппарата в зависимости от текущего значения высоты полета.
Типичным примером параметрической программы управления является закон наведения в системах самонаведения ракет. Закон наведения — это особая программа управления, которая задается через текущие значения координат и скоростей управляемого объекта независимо от того, в какой момент времени они имеют место в процессе движения объекта. Уравнение закона наведения:

где р — первая производная координаты по времени (скорость); f(p) — некоторая функция координаты; р — координата, изменяющаяся во времени.
Например, в задаче сближения двух тел с целью их мягкого контакта приемлемым оказывается нелинейный закон наведения с функцией
f (р) = kp b при значении степени b в интервале J/^ [5].
Контрольные вопросы
- 1. Приведите примеры различных автоматических систем. На какие классы можно разделить эти системы?
- 2. Дайте определения терминам: «объект управления», «управляющее устройство», «управляемые величины», «задающее воздействие», «управляющее воздействие», «возмущающее воздействие».
- 3. По каким принципам можно построить САУ? Приведите функциональные схемы САУ, назовите их достоинства и недостатки.
- 4. Изобразите функциональную схему типовой замкнутой САУ. Из каких основных элементов состоит САУ и какие ее основные задачи?
- 5. Приведите классификацию САУ по следующим основным признакам (сопровождая определениями и примерами): принцип управления, назначение, ошибка в установившемся режиме, характер сигналов на входе и выходе, вид дифференциального уравнения, число управляемых величин, вид используемой энергии.
- 6. Что называется законом наведения? Какой вид имеет закон наведения для случая сближения двух тел для мягкого контакта?
Источник: bstudy.net
ПРИНЦИПЫ ПАРАМЕТРИЧЕСКОГО СТАНОЧНОГО ПРОГРАММИРОВАНИЯ
Сам термин «параметрическое программирование» вошел в оборот недавно в связи с растущими требованиями, предъявляемыми к станкам с ЧПУ. Параметрическое программирование — метод программирования перемещений исполнительных органов станка, основанный на задании этих перемещений с помощью математических функций (параметров), а также с использованием логических выражений.
Современный станок с ЧПУ должен иметь стандартный набор функций для создания программ в стандартном коде, но помимо этого каждый производитель систем ЧПУ стремится создать свой диалоговый, интуитивно понятный интерфейс, дополненный различными функциями и процедурами, позволяющими облегчить программирование и обеспечить удобный контроль за программой, а также визуализацию ее работы.
Технологию параметрического программирования мы покажем на примере выбранного в качестве оборудования для изготовления фасонных борфрез шлифовально-заточного станка мод. ВЗ-392Ф4, оснащенного системой ЧПУ SIEMENS Sinumeric 810Z).
Как и любой современный программный станок, шлифовальнозаточной станок мод. ВЗ-392Ф4 имеет определенный набор подготовительных и вспомогательных функций, позволяющий:
- • программировать движения в режимах линейной и круговой интерполяций, а также в режимах позиционирования (перемещение в заданные координаты с максимально возможной скоростью);
- • применять вычисления с использованием набора стандартных арифметических и тригонометрических функций;
- • программировать в абсолютной и относительной системах координат;
- • применять условные и безусловные переходы;
- • применять подпрограммы до двенадцати уровней вложенности. Для составления программы в системе ЧПУ зарезервированы следующие символы и операторы:
- • буквы A. Z;
- • цифры 0. 9;
- • специальные символы:
% — процент, означает начало и конец программы;
( — открытая скобка, применяется для определения очередности выполнения математических операций;
) — закрытая скобка, применяется для определения очередности выполнения математических операций;
— знак сравнения «больше»;
$ — знак символьной переменной и др.;
• операторы Sin (синус угла), Cos (косинус угла), Asin (арксинус угла), Acos (арккосинус угла), Sqrt (вычисление квадратного корня), Abs (вычисление абсолютной величины), If (оператор условного перехода по программе), GotoB (оператор безусловного перехода по программе вверх), GotoF (оператор безусловного перехода по программе вниз).
Текст управляющей программы для современного станка с ЧПУ представляет собой последовательность кадров. В каждом из кадров могут задаваться вспомогательные, подготовительные или специальные функции, а также буквенный код координаты и значение перемещения по этой координате.
Подготовительные и вспомогательные станочные функции могут быть модальными, когда их действие распространяется на все последующие кадры программы вплоть до их выключения, или немодальными, когда они действуют только в том кадре, где они записаны.
Основные подготовительные, вспомогательные и специальные функции станков с ЧПУ приведены в табл. 1.4.
Основные функции станков с ЧПУ
Перемещение исполнительных органов станка на максимально быстром ходу в указанные координаты. Модальная
Перемещение исполнительных органов станка на рабочей подаче в указанные координаты. Значение подачи указывается в конце кадра. Модальная
Программирование перемещений исполнительных органов станка в абсолютных значениях от начальной точки. Модальная
Программирование перемещений исполнительных органов станка в приращениях от предыдущей точки. Модальная
Перемещение исполнительных органов станка в указанные координаты, используя круговую интерполяцию по часовой стрелке (против часовой стрелки). Модальные
Программируемый останов (с подтверждением). Рабочие органы станка останавливаются до подтверждения продолжения программы с пульта оператора. Немодальные
Включение главного движения станка (шпинделя) по часовой стрелке (против часовой стрелки). Модальные
Включение (выключение) охлаждения. Модальные
Конец программы (с переходом на первый кадр). Модальные
Переход к подпрограмме с номером 01 и т.п.
Выход из подпрограммы. Немодальная
Функция сглаживания. Применяется для сглаживания перемещений и уменьшения динамических нагрузок на координаты станка
Таким образом, задавая последовательность кадров с подготовительными и вспомогательными функциями, а также значения перемещений по станочным координатам, получим текст управляющей программы.
В табл. 1.5 в качестве примера приводится текст управляющей программы для станка с ЧПУ мод. ВЗ-452Ф4 при изготовлении сфероцилиндрической борфрезы.
Рассмотрим более подробно составляющие приведенного текста УП с позиций параметрического программирования.
При запуске программы на станке с ЧПУ сначала производится считывание исходных данных и блока корректоров из подпрограммы
Управляющая программа для станка мод. ВЗ-452Ф4
Кадры управляющей программы
Вызов подпрограммы с исходными данными и корректорами
GOO G90 Х=0 Y=120 Z=0 GOO G90 A=DC(0) B=0
Позиционирование рабочих органов в безопасную зону по координатам X, Y, Z, А, В
Включение шлифовального круга и СОЖ
Включение функции сглаживания перемещений
Вызов подпрограммы расчета исходных данных
R60=R01*R21 R61=R03-(R01*R22) R62=R46*R44 R63=R46*R45 R64=R01*R52 R65=R03-(R01*R53) R07 = R39
Расчет статических данных
Выход из подпрограммы
Вызов подпрограммы выхода исполнительных органов в начальную точку обработки
Организация цикла счетчика обработанных стружечных канавок
GOO G90 X=R60+R28+R08-R29-5 Z=R61 +R10
G01 G90 Y=R30+R09 F3000 G01 G91 X=5 F=R34
Вывод исполнительных органов станка в начальную точку обработки борфрезы
Вызов подпрограммы обработки стружечной канавки
G01 G90 Y=R33/2+R26/2 + 10 F3000 G00G91 A=((360/R27)-R31)
Вывод шлифовального круга из стружечной канавки и деление на следующую стружечную канавку
If R101 <>R27 GotoB Met1
Закрытие цикла счетчика обработанных стружечных канавок
Выход из подпрограммы
X=2.681 Y= 16.824 Z=-0.012 A=0.522 X=2.685 Y=6.673 Z=-0.012 A=0.226 X=2.690 Y=4.914 Z=-0.012 A=0.180 X=2.694 Y=3.964 Z=-0.012 A=0.158 X=2.698Y=3.331 Z=-0.012 A=0.145 X=2.702 Y=2.861 Z=-0.012 A=0.137 X=2.706 Y=2.489 Z=-0.012 A=0.132 X=2.710 Y=2.181 Z=-0.012 A=0.129
Формирование стружечной канавки борфрезы
Окончание табл. 1.5
Кадры управляющей программы
Х=2.714 Y=1.916 Z=-0.012 А=0.126 Х=2.718 Y= 1.683 Z=-0.012 А=0.126 Х=2.722 Y= 1.474 Z=-0.012 А=0.126 Х=2.726 Y=1.283 Z=-0.012 А=0.126 Х=2.730 Y= 1.105 Z=-0.012 А=0.128 Х=2.733 Y=0.939 Z=-0.012 A=0.130 X=2.737 Y=0.780 Z=-0.012 A=0.133 X=2.740 Y=0.629 Z=-0.012 A=0.137 X=2.744 Y=0.481 Z=-0.012 A=0.141 X=2.747 Y=0.338 Z=-0.012 A=0.146 X=2.750 Y=0.196 Z=-0.012 A=0.152 X=2.753 Y=0.056 Z=-0.012 A=0.159 X=22.629 Z=-7.111 A=100.874
Выход из подпрограммы
R04=0;Diametr opravki kasania R05=1 ;Priznak obrabotki kanavki R07=0;Priznak obrabotki strugkoloma R08=0;Korrektor kanavki po X R09=0;Korrektor kanavki po Y R10=0;Korrektor kanavki po Z R20=17.446 R21 =0.954 R22=0.300 R23=0.770 R24=1 R25=0.000 R26=10.000 R27=18.0 R28=4.770 R29=54.382 R30=0.000 R31 =104.133 R32=0.766 R33=100.0000
R34=100.00 R35 = 100.00 R36=300.00 R37=0.00
Модуль исходных данных (параметров) и блок корректоров
Выход из подпрограммы
Выключение шлифовального шпинделя и С0Ж
G01 G90 X=0 Y= 120 Z=0 F7000
Вывод исполнительных органов в безопасную
GOO G90 A=DC(0) B=0
с номером L99. Далее параметры R21 и R22 используются при расчете параметров R60 и R61 (в подпрограмме L01), которые, в свою очередь, характеризуют точку начала профилирования стружечной канавки (см. блок «вывод исполнительных органов станка в начальную точку обработки борфрезы»). Также в подпрограмме L99 можно, изменяя параметр R09, изменить глубину стружечной канавки (. G01 G90 Y=R30+R09 F3000. ; см. блок «вывод исполнительных органов станка в начальную точку обработки борфрезы»), а изменяя параметр R34 — изменить рабочую подачу (. G01 G91 Х=5 F=R34. ; см. тот же блок).
Таким образом, изменяя (корректируя) параметры в подпрограмме L99 (R08, R09, R10), можно влиять на профилирование изготавливаемого инструмента как в отношении геометрических параметров (глубина канавки, начальная точка и т.п.), так и в отношении технологических параметров (подача, число проходов при профилировании и т.п.).
Источник: studref.com
Параметрическое линейное программирование.
Параметрическое программирование представляет собой один из разделов математического программирования, изучающий задачи, в которых целевая функция или ограничения зависят от одного или нескольких параметров.
Необходимость рассмотрения подобных задач обусловлена различными причинами. Одной из основных является та, что исходные данные для численного решения любой реальной задачи оптимизации в большинстве случаев определяются приближенно или могут изменяться под влиянием каких-то факторов, что может существенно сказаться на оптимальности выбираемой программы (плана) действий. Соответственно, разумно указывать не конкретные данные, а диапазон возможного изменения данных, чтобы в результате решения иметь наилучшие планы для любого варианта исходных данных.
С математической точки зрения параметрическое программирование выступает как одно из средств анализа чувствительности решения к вариации исходных данных, оценки устойчивости решения.
Заметим, что существуют различные подходы к подобному анализу (например, на основе постановки двойственной задачи). Здесь мы, не ссылаясь на двойственные оценки, рассмотрим самые простейшие варианты решения для самых простейших параметрических программ.
1) Рассмотрим задачу параметрического линейного программирования, в которой только коэффициенты целевой функции линейно зависят от некоторого единственного параметра λ (времени, температуры и т. п.):
Отыскать максимум (или минимум) функции:
Если обратиться к геометрической интерпретации задачи, то можно заметить, что вектор-градиент линейной формы определяется её параметром. Например, для целевой функции
при различных значениях параметра λ градиент определяет различные направления роста функции.
На рисунке нетрудно видеть, что, если при некотором значении параметра максимум достигается в вершине A, то небольшая вариация этого значения несколько изменит направление градиента, но не изменит положение точки максимума. Отсюда напрашивается вывод, что некоторый план, оптимальный при при оптимален и в окрестности , т. е. при , где .
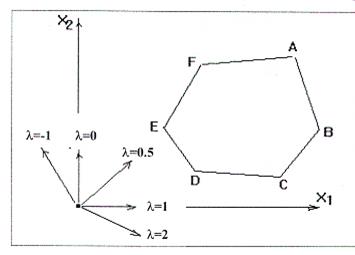
Можно заметить, что при градиенте, ставшем перпендикулярным некоторой стороне многоугольника планов, имеем два разных оптимальных опорных плана с одним и тем же значением линейной формы, откуда можно утверждать непрерывность экстремума линейной формы по λ.
В случае неограниченности множества планов можно утверждать, что если линейная форма не ограничена при , то она не ограничена при всех λ, больших или меньших .
Алгоритм для решения задач параметрического линейного программирования в случае зависимости от параметра коэффициентов целевой функции (примеры решения подобных задач приведены ниже):
1. Вначале решается задача (12.1)-(12.2) прямым симплекс методом, и вместо подставляем удобное нам число из заданного промежутка , но не заменяем конкретным числом.
2. Получив оптимальный план (все ), отбрасываем промежуток, для которого этот план оптимален. И продолжаем решение полученной симплекс таблицы для тех , для которых план не является оптимальным. Получив оптимальный план , отбрасываем промежуток, для которого этот план оптимален. Решение продолжается до тех пор, пока для всех не будет найден оптимальный план или установлено, что задача не разрешима.
2) В случае зависимости от параметра компонент вектора правых частей ограничений, т. е. решения задачи поиска экстремума функции
Алгоритм решения задачи в случае зависимости от параметра компонент вектора правых частей ограничений:
1. Вначале решается задача (12.3)-(12.4) двойственным симплекс методом, и вместо подставляем удобное нам число из заданного промежутка , но не заменяем конкретным числом.
2. Получив оптимальный план (все ), отбрасываем промежуток, для которого этот план оптимален. И продолжаем решение полученной симплекс таблицы для тех , для которых план не является оптимальным. Получив оптимальный план , отбрасываем промежуток, для которого этот план оптимален. Решение продолжается до тех пор, пока для всех не будет найден оптимальный план или установлено, что задача не разрешима.
Во избежание сложностей, связанных с требованием сохранения неотрицательности компонент плана при любых λ (сохранения неотрицательности правой части системы уравнений при всех ее тождественных преобразованиях), достаточно постановить двойственную задачу, воспользоваться вышеупомянутым алгоритмом решения задач параметрического линейного программирования при зависимости от параметра коэффициентов целевой функции и с помощью известных двойственных соотношений находить решение исходной задачи.
Пример 12.1.Рассмотрим задачу минимизации
Решение. Как обычно, приводим задачу к канонической форме и с использованием метода искусственного базиса отыскиваем начальный опорный план c .
| С баз | Базис 1 | План Хбаз | λ | -λ | -1 | М |
| А1 | А2 | А3 | А4 | А5 | А6 | А7 |
| М | А7 | -3 | -1 | -1 | ||
| А6 | -2 | -1 | ||||
| Δk | 5М | 3М- λ | -3М+ λ | -М+1 | М-1 | -М |
Так как определяющую роль на этом шаге решения играет величина M, превышающая все величины задачи, то не обращаем внимания на и, обнаружив невыполнение критерия оптимальности для , вводим в базис вместо (переходим к следующему опорному плану):
| С баз | Базис 2 | План Хбаз | λ | -λ | -1 |
| А1 | А2 | А3 | А4 | А5 | А6 |
| А4 | -3 | -1 | -1 | ||
| А6 | -5 | -1 | |||
| Δk | 3 — λ | -3 + λ | -1 |
Полученный опорный план c будет оптимальным, если все значения неположительны, т. е.
Решаем систему двух линейных неравенств и обнаруживаем, что найденный план оптимален при .
Исследуем оставшиеся из заданного диапазона значения λ.
Пусть . Тогда и вектор подлежит вводу в базис, но в силу неположительности его компонент приходим к выводу, что при линейная форма задачи не ограничена снизу.
Пусть . Тогда и в базис вводится вектор :
| С баз | Базис 3 | План Хбаз | λ | -λ | -1 |
| А1 | А2 | А3 | А4 | А5 | А6 |
| А4 | 1/5 | -1 | -2/5 | -3/5 | |
| λ | А1 | 8/5 | -1 | -1/5 | 1/5 |
| Δk | (8λ+1)/5 | -(λ+2)/5 | (λ-3)/5 |
Полученный опорный план является оптимальным, если все значения неположительны, т. е.
Решая эту систему линейных неравенств, обнаруживаем, что найденный план c оптимален при .
Пусть . Тогда и вектор подлежит вводу в базис; в силу неположительности его компонент приходим к выводу, что при линейная форма задачи не ограничена снизу.
Таким образом, мы получили решение задачи:
Пример 12.2. Рассмотрим задачу максимизации
Решение. Чтобы решить эту задачу, достаточно решить двойственную к ней задачу, имеющую вид:
Данная задача будет решаться с помощью прямого симплекс метода. Приводим двойственную задачу к канонической форме (умножив предварительно второе и третье неравенства на (-1)) и начинаем обычное решение обычным симплексным методом. Заметьте, что указанное умножение тождественно смене знака у переменных и исходной задачи.
| С баз | Базис 1 | План Yбаз | 3+λ | 5-λ | M |
| А1 | А2 | А3 | А4 | А5 | А6 |
| M | А6 | -1 | |||
| А4 | -1 | ||||
| А5 | -1 | -1 | |||
| Δk | M | M-3-λ | 2M-5+λ | -M |
| С баз | Базис 2 | План Yбаз | 3+λ | 5-λ | M |
| А1 | А2 | А3 | А4 | А5 | А6 |
| 3+λ | А1 | -1 | |||
| А4 | -1 | ||||
| А5 | -1 | ||||
| zk | 3+λ | 3+λ | 6+2λ | -(3+λ) | 3+λ |
| Δk | 1+3λ | -(3+λ) | 3+λ-M |
Найденный план оптимален, если и , т. е. при , .В строке (в позициях 6, 4, и 5 в соответствии с начальным базисом) находим решение прямой задачи: , .
Пусть . Попытка ввода в базис вектора обнаруживает, что в этом случае линейная форма решаемой (двойственной) задачи не ограничена снизу и, следовательно, ограничения исходной задачи противоречивы.
| С баз | Базис 3 | План Yбаз | 3+λ | 5-λ | M |
| А1 | А2 | А3 | А4 | А5 | А6 |
| 5-λ | А2 | 1/2 | 1/2 | -1/2 | 1/2 |
| А4 | 1/2 | -3/2 | 1/2 | -1/2 | |
| А5 | 5/2 | -1/2 | -1/2 | 1/2 | |
| zk | (5-λ)/2 | (5-λ)/2 | 5-λ | -(5-λ)/2 | (5-λ)/2 |
| Δk | -(3λ+1)/2 | -(5-λ)/2 | -M+… |
Решаем систему неравенств , . Обнаруживаем, что при , , .
Продолжаем решение задачи при . Получаем:
| С баз | Базис 4 | План Yбаз | 3+λ | 5-λ | M |
| А1 | А2 | А3 | А4 | А5 | А6 |
| 5-λ | А2 | -1 | |||
| А4 | -3 | -1 | |||
| А5 | -2 | ||||
| zk | 5-λ | -(5-λ) | 5-λ | 5-λ | |
| Δk | -8 | 5-λ | -M |
Видим, что при , , , . Задача решена:
| Диапазон λ | Сопряженная задача | Исходная задача |
| λ | L(y, λ)→ — ∞ | Ограничения противоречивы |
| -3≤λ≤-1/3 | yopt = (1,0) | xopt = (3+ λ,0,0), L(xopt) =3+ λ |
| -1/3≤λ≤5 | yopt = (0,1/2) | xopt =((5- λ)/2,0,0), L(xopt)=(5- λ)/2 |
| λ≥5 | yopt = (0,1) | xopt = (0,-5+ λ,0) , L(xopt)=5- λ |
Увы, в случае зависимости от параметра компонент матрицы ограничений столь простого универсального подхода к решению не существует. Нет простых решений и в случае зависимости характеристик задачи от нескольких параметров.
Варианты заданий для самостоятельной работы
Решить задачу параметрического линейного программирования. Объяснить полученные результаты.
Источник: studopedia.ru