Mathcad — это популярная система компьютерной математики, предназначенная для автоматизации решения массовых математических задач в самых различных областях науки, техники и образования. Название системы происходит от двух слов -MATHematica (математика) и CAD (Computer Aided Design — системы автоматизированного проектирования, или САПР). Так что вполне правомерно считать Mathcad математическими САПР.
Основные возможности
Mathcad содержит сотни операторов и встроенных функций операторов для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции с скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие.
Среди возможностей Mathcad можно выделить:
Решение дифференциальных уравнений, в том числе и численными методами
Построение двумерных и трёхмерных графиков функций (в разных системах координат, контурные, векторные и т. д.)
Использование греческого алфавита как в уравнениях, так и в тексте
0 Базовые возможности MathCad
Выполнение вычислений в символьном режиме
Выполнение операций с векторами и матрицами
Символьное решение систем уравнений
Поиск корней многочленов и функций
Проведение статистических расчётов и работа с распределением вероятностей
Поиск собственных чисел и векторов
Вычисления с единицами измерения
Интеграция с САПР системами, использование результатов вычислений в качестве управляющих параметров
С помощью Mathcad инженеры могут документировать все вычисления в процессе их проведения.
Из чего состоит библиотека встроенных функций.
Мощная библиотека встроенных функций позволяет решать широкий круг инженерных и математических задач:
- Решение задач с использованием численных методов
- Решение систем уравнений, обыкновенных дифференциальных уравнений, уравнений в частных производных с помощью различных методов
- Поиск корней многочленов и функций
- Символьные вычисления выражений, в том числе систем уравнений
- Работа с единицами измерения, автоматическая проверка единиц измерения
- Создание 2D, 3D, полярных и контурных графиков
- Работа с векторами и матрицами
- Инструменты программирования
- Возможность вставки ссылок на другие листы Mathcad для повторного использования общих инженерных методов
- Интеграция с другими инженерными приложениями и инструментами моделирования, такими как Autocad, Creo, Pro/ENGINEER, Ansys, Excel
Типы данных.

Для ввода числа в других системах счисления: двоичной (binary), восьмеричной (octal) или шестнадцатеричной (hexadecimal), сделайте следующее:
1. Введите его представление в соответствующей системе, применяя лишь корректные символы (для двоичной системы допустимы только цифры О и 1; для восьмеричной — цифры от 0 до 7, для шестнадцатеричной — цифры от 0 до 9 и буквы от а до f) Например, число 34 в двоичной системе представлено такой последовательностью: 100010.
Основные возможности программы MatCAD
2. После ввода последнего символа числа введите ь (для двоичного числа), о (для восьмеричного числа), или h (для шестнадцатеричного).
Использование чисел в других системах счисления иллюстрируется листингом 4.2. Обратите внимание, что вывод осуществляется все равно в десятичной системе.
Листинг 4.2. Ввод чисел в других системах исчисления
Примечание
В логических функциях используются битовые числа (ложь или истина). Они в MathCAD обозначаются обычными действительными числами о и 1.
4.1.2. Комплексные числа
Большинство операций в среде MathCAD по умолчанию осуществляются над комплексными числами. Комплексное число является суммой действительного и мнимого числа, получающегося путем умножения любого действительного числа на мнимую единицу (imaginary unit) i. По определению,
i = корень -l ИЛИ i 2 =-l.
Чтобы ввести мнимое число, например 3i:
1. Введите действительный сомножитель (з).
2. Введите символ «i» или «j» непосредственно после него.
Для ввода мнимой единицы надо нажать клавиши , . Если просто ввести символ «i», то MathCAD интерпретирует его как переменную i. Кроме того, мнимая единица имеет вид 1i, только когда соответствующая формула выделена. В противном случае мнимая единица отображается просто как i (рис. 4.1).

Рис. 4.1. Ввод мнимой единицы
Комплексное число можно ввести в виде обычной суммы действительной и мнимой частей, или в виде любого выражения, содержащего мнимое число. Примеры ввода и вывода комплексных чисел иллюстрируются листингом 4.3.
Листинг 4.3. Комплексные числа

Для работы с комплексными числами имеются несколько простых функций и операторов (см. разд. «Функции работы с комплексными числами» гл. 10), действие которых показано в листинге 4.4.
Листинг 4.4. Функции работы с комплексными числами

Примечание
Можно выводить мнимую единицу в результатах вычислений не как i, а как j. Для смены представления выберите нужное в списке Imaginary Value (Мнимое значение) диалогового окна Result Format (Формат результата), доступного по команде Format / Result / Display Options (Формат / Результат / Опции отображения).
4.1.3. Встроенные константы
Некоторые имена в MathCAD зарезервированы под системные перемени которые называются встроенными константами (built-in constants). Встроные константы делятся на два типа: математические, хранящие значение некоторых общеупотребительных специальных математических СИМВОЛОВ системные, определяющие работу большинства численных алгоритмов, реализованных в MathCAD.
Математические константы (math constants)
— символ бесконечности (вводится клавишами ++
— е — основание натурального логарифма (клавиша );
— число «пи» (вводится клавишами ++
);
— i, j — мнимая единица (вводится клавишами , или , );
— % — символ процента, , эквивалентный o.o1
Математические константы по-разному интерпретируются при численны символьных вычислениях. Вычислительный процессор просто воспринимает их как некоторые числа (листинг 4.5), а символьный распознает каждое из них, исходя из математического контекста, и способен выдавать матемаческие константы в качестве результата.
Листинг 4.5. Значения математических констант

При желании можно изменить значение любой из перечисленных констант или использовать их в качестве переменных в расчетах (см. листинг 4.1, в котором переопределена константа е). Разумеется, если присвоить константе новое значение, прежнее станет недоступным.
Системные переменные (system variables)
-TOL — точность численных методов (см. часть III);
-CTOL — точность выполнения выражений, используемая в некоторых численных методах (см. часть III);
-ORIGIN — номер начального индекса в массивах (см. разд. 4.3.1);
-PRNPRECISION — установка формата данных при выводе в файл (см. гл.15);
— PRNCOLWIDTH — установка формата столбца при выводе в файл (см. гл. 15);
— CWD — строковое представление пути к текущей рабочей папке.
Предустановленные значения системных переменных перечислены в листинге 4.6. Их можно поменять в любой части документа, присвоив соответствующей переменной новое значение. Кроме того, переопределение значения переменной для всего документа производится при помощи команды Math / Options / Built-in Variables (Математика / Опции / Встроенные переменные) в диалоговом окне Math Options (Опции математики), приведенном на рис. 4.2. Чтобы в любой момент вернуть значения по умолчанию, нажмите кнопку Restore Defaults (Восстановить установки по умолчанию).
Листинг 4.6. Предустановленные значения системных переменных


Рис. 4.2. Вкладка Built-in Variables диалога Math Options
4.1.4. Строковые выражения
Значением переменной или функции может быть не только число, но и строка, состоящая из любой последовательности символов, заключенной в кавычки (листинг 4.7). Для работы со строками в MathCAD имеется несколько встроенных функций (см. разд. «Строковые функции» гл. 10).
Листинг 4.7. Ввод и вывод строк

Примечание
Совершенно аналогичным образом можно определять пользовательские функции строкового типа.
Источник: infopedia.su
Основные возможности MathCad
Mathcad содержит сотни операторов и встроенных функций для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции с скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие.
Среди возможностей Mathcad можно выделить:
· Решение дифференциальных уравнений, в том числе и численными методами
· Построение двумерных и трёхмерных графиков функций (в разных системах координат, контурные, векторные и т. д.) (Рисунок 2.2)
Рисунок 2.2 – Трёхмерный график, построенный в Mathcad
· Использование греческого алфавита как в уравнениях, так и в тексте
· Выполнение вычислений в символьном режиме
· Выполнение операций с векторами и матрицами
· Символьное решение систем уравнений
· Поиск корней многочленов и функций
· Проведение статистических расчётов и работа с распределением вероятностей
· Поиск собственных чисел и векторов
· Вычисления с единицами измерения
· Интеграция с САПР системами, использование результатов вычислений в качестве управляющих параметров
С помощью Mathcad инженеры могут документировать все вычисления в процессе их проведения.
Mathcad относится к системам компьютерной алгебры, то есть средств автоматизации математических расчетов. В этом классе программного обеспечения существует много аналогов различной направленности и принципа построения. Наиболее часто Mathcad сравнивают с такими программными комплексами, как Maple, Mathematica, MATLAB, а также с их аналогами MuPAD, Scilab, Maxima и др. Впрочем, объективное сравнение осложняется в связи с разным назначением программ и идеологией их использования.
Maple, MATLAB и Mathematica — это языки программирования. Языки программирования гибкие и мощные, но трудные в использовании и требующие длительного времени на изучение. Поэтому, пользовательский интерфейс сложен, в нем легко допускать ошибки, которые вынуждают проверять и отлаживать весь код. Программирование не визуально и не интерактивно.
Невозможно поменять несколько строк в программе и автоматически увидеть результаты. Для этого вам потребуется перекомпилировать и перезапустить программу. Кроме этого, существуют сложности в понимании и использовании программистами чужих вычислений, для чего требуется вникать вглубь процесса.
Разработчики Mathcad сделали ставку на расширение системы в соответствии с потребностями пользователя. Для этого назначены дополнительные библиотеки и пакеты расширения, которые можно приобрести отдельно и которые имеют дополнительные функции, встраиваемые в систему при установке, а также электронные книги с описанием методов решения специфических задач, с примерами действующих алгоритмов и документов, которые можно использовать непосредственно в собственных расчетах. Кроме того, в случае необходимости и при условии наличия навыков программирования в C, есть возможность создания собственных функций и их прикрепления к ядру системы через механизм DLL (Рисунок 2.3).
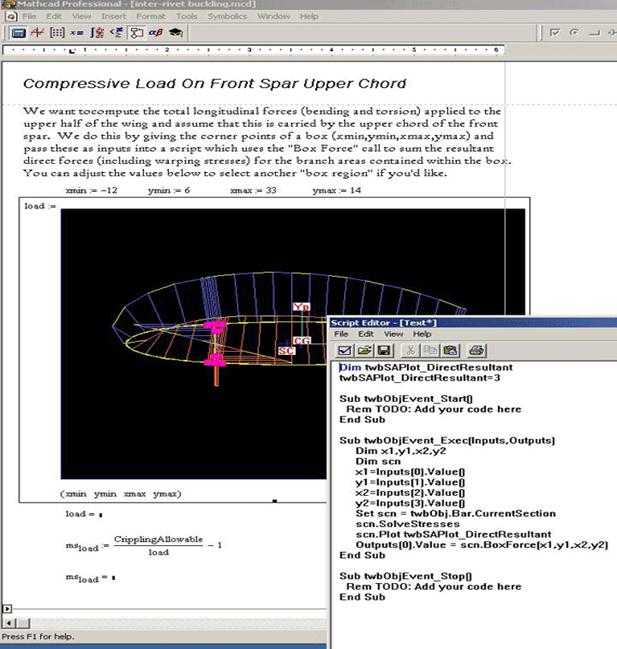
Рисунок 2.3 – Пример рабочего окна программы
Mathcad, в отличие от Maple, изначально создавался для численного решения математических задач, он ориентирован на решение задач именно прикладной, а не теоретической математики, когда нужно получить результат без углубления в математическую суть задачи. Впрочем, для тех, кому нужны символьные вычисления и предназначено интегрированное ядро Maple (с версии 14 — MuPAD). Особенно это полезно, когда речь идет о создании документов образовательного назначения, когда необходимо продемонстрировать построение математической модели, исходя из физической картины процесса или явления. Символьное ядро Mathcad, в отличие от оригинального Maple (MuPAD) искусственно ограничено (доступно около 300 функций), но этого в большинстве случаев вполне достаточно для решения задач инженерного характера.
Более того, опытные пользователи Mathcad обнаружили, что в версиях до 13 включительно есть возможность не слишком сложным способом задействовать почти весь функциональный арсенал ядра Maple (так называемые «недокументированные возможности»), что приближает вычислительную мощность Mathcad к Maple.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник: studopedia.ru
Основные возможности:
Mathcad содержит сотни операторов и встроенных функций для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции со скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие.
Среди возможностей Mathcad можно выделить:
- Решение дифференциальных уравнений, в том числе и численными методами
- Построение двумерных и трёхмерных графиков функций (в разных системах координат, контурные, векторные и т. д.)
- Использование греческого алфавита как в уравнениях, так и в тексте
- Выполнение вычислений в символьном режиме
- Выполнение операций с векторами и матрицами
- Символьное решение систем уравнений
- Аппроксимация кривых
- Выполнение подпрограмм
- Поиск корней многочленов и функций
- Проведение статистических расчётов и работа с распределением вероятностей
- Поиск собственных чисел и векторов
- Вычисления с единицами измерения
- Интеграция с САПР-системами, использование результатов вычислений в качестве управляющих параметров
Назначение:
Mathcad относится к системам компьютерной алгебры, то есть средствавтоматизацииматематических расчетов. В этом классепрограммного обеспечениясуществует много аналогов различной направленности и принципа построения. Наиболее часто Mathcad сравнивают с такими программными комплексами, какMaple,Mathematica,MATLAB, а также с их аналогамиMuPAD,Scilab,Maximaи др.
Впрочем, объективное сравнение осложняется в связи с разным назначением программ и идеологией их использования. Система Maple, например, предназначена главным образом для выполнения аналитических (символьных) вычислений и имеет для этого один из самых мощных в своем классе арсенал специализированных процедур и функций (более 3000).
Такая комплектация для большинства пользователей, которые сталкиваются с необходимостью выполнения математических расчетов среднего уровня сложности, является избыточной. Возможности Mapleориентированы на пользователей — профессиональныхматематиков; решения задач в среде Maple требуют не только умения оперировать какой-либо функции, но и знания методов решения, в неё заложенных: во многих встроенных функциях Maple фигурирует аргумент, задающий метод решения.
То же самое можно сказать и о Mathematica. Это одна из самых мощных систем, имеет чрезвычайно большую функциональную наполненность (есть даже синтезированиезвука).Mathematicaобладает высокой скоростью вычислений, но требует изучения довольно необычногоязыка программирования. Разработчики Mathcad сделали ставку на расширение системы в соответствии с потребностями пользователя.
Для этого назначены дополнительные библиотеки и пакеты расширения, которые можно приобрести отдельно и которые имеют дополнительные функции, встраиваемые в систему при установке, а также электронные книги с описанием методов решения специфических задач, с примерами действующих алгоритмовидокументов, которые можно использовать непосредственно в собственных расчетах. Кроме того, в случае необходимости и при условии наличия навыков программирования вC, есть возможность создания собственных функций и их прикрепления к ядру системы через механизмDLL.
Mathcad, в отличие от Maple, изначально создавался для численного решения математических задач, он ориентирован на решение задач именноприкладной, а не теоретической математики, когда нужно получить результат без углубления в математическую суть задачи. Впрочем, для тех, кому нужны символьные вычисления и предназначено интегрированное ядроMaple(с версии 14 —MuPAD). Особенно это полезно, когда речь идет о создании документов образовательного назначения, когда необходимо продемонстрировать построение математической модели, исходя из физической картины процесса или явления. Символьное ядро Mathcad, в отличие от оригинального Maple (MuPAD), искусственно ограничено (доступно около 300 функций), но этого в большинстве случаев вполне достаточно для решения задачинженерногохарактера. Более того, опытные пользователи Mathcad обнаружили, что в версиях до 13 включительно есть возможность не слишком сложным способом задействовать почти весь функциональный арсенал ядра Maple(так называемые «недокументированные возможности»), что приближает вычислительную мощность Mathcad кMaple
Источник: studfile.net