Часто при решении задач приходится многократно вычислять значение по одним и тем же алгоритмам. Такие многократно повторяемые алгоритмы называются циклами. Различают циклы с заданным и неизвестным числом повторений. К последним относятся итерационные циклы, характеризующиеся последовательным приближением к искомому значению с заданной точностью.
Для организации цикла необходимо выполнить следующие действия: 1) задать перед циклом начальное значение переменной, изменяющейся в цикле; 2) изменять переменную перед каждым новым повторением цикла; 3) проверять условие окончания или повторения цикла; 4) управлять циклом, т.е. переходить к его началу, если он не закончен, или выходить из него по окончании. Последние три функции выполняются многократно.
Переменная, изменяющаяся в цикле, называется параметром цикла.
1. Вычислить значения функции , если Х задано массивом, состоящим из 40 элементов.
2. Вычислить и вывести на печать положительные значения функции у=sin (nx) ‑ cos (n/x) при n = 1, 2, …, 50.
Передача массива в функцию. Как передать массив в функцию. C++ для начинающих. Урок #35.
3. Вычислить значения функции z = x k /k, большие а, если k=1, 2, ….
4. Вычислить значения функции у = а 3 /(а 2 + х 2 ) при х, изменяющемся от 0 до 3 с шагом 0,1.
5. Напечатать таблицу значений аргумента х и функции
у(х) = а 3 /(а 2 + х 2 ) при значении х, изменяющихся от 0 до 3 с шагом 0,1.
6. Составить программу для вычисления значения функции у = при одновременном изменении аргументов t от 2 до 3 с шагом 0,2 и х от 1 до 2 для а = ‑2,1.
7. Составить программу вычисления n! (1 . 2 . 3 . 4 . . . n):
8. Составить программу, вычисляющую экстремальное значение функции при изменении аргумента х от 0 до 4 с шагом h.
9. Вычислить:
а) у = (2n ‑1)! = … , n >0;
10. Вычислить: у = .
11. Определить, является ли заданное натуральное число совершенным, т.е. равным сумме всех своих делителей, кроме самого этого числа (например, число 6 совершенно: 6=1+2+3).
12. Дано целое n >2. Напечатать простые числа из диапазона [2, n].
13. Найти сумму цифр заданного натурального числа.
14. Вычислить k ‑ количество точек с целочисленными координатами, попадающих в круг радиуса R (R>0) с центром в начале координат.
15. Напечатать в возрастающем порядке все трехзначные числа, в десятичной записи которых нет одинаковых цифр.
16. Даны целое n и вещественные числа Рассматривая пары как координаты точек на плоскости, определить радиус наименьшего круга (с центром в начале координат), внутрь которого попадают все эти точки.
17. Напечатать все простые делители натурального числа.
18. Уравнение (предложена М.В. Дякиным).
Дана последовательность , ‑ натуральное число. Квадратные скобки обозначают в формуле взятие целой части (округление до ближайшего меньшего целого числа). Обозначим .
Написать программу, которая для заданного натурального решает уравнение ,
где — обозначение числа — факториал: .
Программа должна найти и сообщить:
Возврат нескольких значений функции через ссылки. Как вернуть несколько значений функции. Урок #52
1) точное значение x в виде несократимой дроби;
2) сумму цифр числителя и сумму цифр знаменателя этой дроби.
Образец вывода результата:
Число 6, числитель дроби X=10, знаменатель дроби X=63.
Сумма цифр числителя =1, сумма цифр знаменателя =9.
19. Задача « Кучи и яма»(предложена А.Б. Дернятиным).
Имеются яма и несколько куч (не более пяти) кирпичей. Разрешается перекладывать кирпичи из куч в яму по следующему правилу: если количество кирпичей в куче больше, чем в яме, то можно переложить столько кирпичей, сколько находится в яме в данный момент. Требуется разработать алгоритм, который позволяет уложить в яму как можно больше кирпичей.
Образец вывода результатов:
К1=150001 К2=81234 Я=70000 было
К1=150001 К2=11234 Я=140000 в яму из кучи 2‑й
К1=10001 К2=11234 Я=280000 в яму из кучи 1‑й
20. Представления натурального числа (предложена Д.Я.Шараевым).
Пример. N=4. S=2. (1 2 +1 2 +1 2 +1 2 =4, 2 2 =4)
21. Задача «Многоугольник»(предложена Н.Ю. Лукояновым).
На плоскости декартовыми координатами своих вершин дан выпуклый -угольник. Его вершины пронумерованы от 1 до n в порядке следования против часовой стрелки. Задан номер . Требуется провести через -вершину -угольника два луча (назовем их a и b) так, чтобы эти лучи делили -угольник на три равновеликие по площади части.
Входные данные: — число вершин; (х1, y1), (x2, y2), …, (xn, yn) — координаты 1-й, 2-й, и т.д. -й вершины соответственно; — номер выделенной вершины.
Выходные величины: координаты (ха, ya) и (xb, yb) точек пересечения лучей a и b с границей -угольника.
Алгоритмы работы с рядами
При работе с рядами обычно составляют рекуррентную формулу, которая задает значение i+1-го члена ряда (Y(i+1)) через значения предыдущих членов, чаще ‑ i-го члена ряда (Y(i)). Обычно используют отношение i+1-го члена к i-му члену, подставляют их значения, и после преобразований получается рекуррентная формула.
Пример. Вычислить значение членов бесконечного ряда точностью до члена . Считать, что требуемая точность (ε) достигнута, если очередное слагаемое по модулю меньше указанной точности и все последующие слагаемые можно уже не учитывать. Определим рекуррентную формулу Y(i+1)/Y(i)=(x ( i+1) /(i+1)!)/(x i /i!)=x/i. Получим рекуррентную формулу Y(i+1)=Y(i)*x/(i+1).
1. Вычислить сумму членов для следующих рядов с точностью до 10 -4 :
Для вычисления текущего значения члена ряда использовать рекуррентную формулу , где n ‑ номер члена ряда. Начальное значение у принять равным ;
Текущий член ряда вычислять, используя рекуррентную формулу.
2. Составить программу вычисления значений членов убывающей последовательности … с точностью до10 -4 .
3. Составить программу вычисления членов бесконечного ряда
с точностью до10 -4 .
4. Не используя стандартные функции (за исключением abs), вычислить с точностью до 10 -4 :
5. Вычисление f = 10!
6. Вычислить:
а) у = cos(x)+ cos(x 2 ) + cos(x 3 ) +…+cos(x 30 );
б) у = 1! + 2! + 3! + …+ n! (n>1);
в) у ‑ первое из чисел sin(x), sin(sin(x)), sin(sin(sin(x,…))), меньшее по модулю 10 -4 .
7. Числа Фибоначчи («fn») определяются по формулами f0 = f1 = 1;
а) определить четвертое число Фибоначчи;
б) вычислить первое число Фибоначчи, большее m (m > 1);
в) вычислить s ‑ сумму всех чисел Фибоначчи, которые не превосходят 1000.
Источник: megalektsii.ru
Вычисление значения функции при изменении аргумента в указанном диапазоне и с заданным шагом — Turbo Pascal
Составить программу вычисления значения функции при изменении аргумента в указанном диапазоне и с заданным шагом. Организовать вывод значения аргумента и вычисленного значения функции в виде таблицы и проверить правильность выполнения программы с помощью тестового варианта. Переменные даны в прикрепленном файле
Код к задаче: «Вычисление значения функции при изменении аргумента в указанном диапазоне и с заданным шагом»
Листинг программы
uses crt; var x,y,a,xn,xk,dx:real; begin clrscr; a:=2.3; xn:=0.2; xk:=2.8; dx:=0.2; x:=xn-dx; while x begin x:=x+dx; if x1)and(x <2)then y:=sqr(x-2)+6 else y:=3*sin(x)/cos(x); writeln(‘x=’,x:4:1,’ y=’,y:5:2);<выводим>end; readln end.
Источник: studassistent.ru
Программа вычисления функции для заданных значений аргументов с использованием рядов

Составить программу вычисления функции для заданных значений аргумен-тов с использованием рядов. Суммы рядов вычислить с погрешностью e.
В программе предусмотреть защиту от зацикливания итерационного процесса, подсчет и вывод на печать числа итераций, за которое удается найти сумму ряда с заданной погрешностью. Для проверки программы вывести на печать значения функций f1 и f2, вычисленные с помощью рядов и соответствующих им аналитических зависимостей.








1- x 2 /2!+. +(-1) n* x 2n /(2n)!+
-1/2ln(1-2xcos p/3+x 2
Погрешность: 10 -3
Теоретическая часть
При вычислении значения функции с использованием функционального ряда
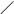

 fn (x) = f1(x) + f2(x) + . + fn(x) + . , (1)
fn (x) = f1(x) + f2(x) + . + fn(x) + . , (1)

n=1
задача сводится к последовательному вычислению частичных сумм S1(x), S2(x), . , Sn(x). , где



 Sn(x) = fi (x).
Sn(x) = fi (x).
Для сходящегося ряда существует предел
lim Sn(x) = S(x), где S(x) — сумма функционального ряда. При вычислении суммы равномерно сходящегося ряда с заданной погрешностью E в качестве окончательного результата принимается значение частичной суммы Sn (x), для которой выполняется условие
т.е. абсолютная величина очередного слагаемого не превышает значения E.
В общем случае начальное значение номера члена ряда в формуле (1) может быть отличным от единицы (например, равным нулю). Обозначив его через k, получим

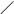

 S(x) = f n(x). (3)
S(x) = f n(x). (3)
Процесс вычисления суммы ряда (1) определяется рекуррентным соотношением
суммирование считается законченным при выполнении условия достижения заданной точности (2). Начальное значение суммы принимается равным нулю. Алгоритм вычисления суммы функционального ряда приведен на рис. 1.
В схеме алгоритма на рис. 1 и последующих алгоритмах данной темы входными параметрами для алгоритма вычисления суммы ряда являются значения x и e (блок 1), выходными — значение суммы S (блок 7). Переменная f представляет собой значение очередного члена ряда. Поскольку в вычислениях по рекуррентной формуле (3) одновременно участвуют лишь два значения: Sn-1(x) и Sn (x), в схеме алгоритма для их обозначения используется одна переменная S (блок 4). Значение S изменяется при прибавлении очередного члена суммы: справа от знака присваивания значение переменной S соответствует предыдущему значению суммы Sn-1 (x), слева — текущему Sn(x).
При составлении алгоритма вычисления суммы конкретного ряда в блоке (3) параметр k заменяется значением номера начального члена этого ряда, в блоке 4 величина fn(x) — формулой общего члена данного ряда.

1

Вход (x,e)

S=0

3

n=k



 4
4

5

n=n+1


 6
6

 — f > e
— f > e




7 +

Выход (S)
Обычно формула общего члена ряда принадлежит к одному из следующих типов:
а) cos nx / n; sin(2n-1)x / 2n-1; cos 2nx / 4n 2 — 1;
б) x n / n!; (-1) n x 2n+1 / (2n+1); x 2n / (2n)!;
в) n 2 +1 / n! (x / 2) n ; (-1) n cos nx / n 2 ; x 4n+1 / 4n+1.
В случае “а” вычисления будут наиболее эффективными, если каждый член ряда вычислять по его общей формуле. Вычисление суммы ряда в этом случае организуется по схеме, приведенной на рис. 1.
В случае “б” в формулу общего члена ряда входят целые степени и факториалы. Для вычисления fn (x) при этом целесообразно использовать рекуррентные соотношения, т.е. вычислять последующий член ряда через предыдущий. Это позволяет существенно сократить объем вычислений. Кроме того, непосредственное вычисление члена ряда по общей формуле в ряде случаев невозможно, например, из-за наличия факториала. Очередной член ряда можно определить через предыдущий следующим образом:
Похожие материалы
- Запросы — в центре внимания рынок сбыта. Конструирование запросов. Режимы представления запроса
- Отработка ассемблером ошибочных ситуаций. Команды управления процессом ассемблирования
- Архивирование данных. Назначение программ-архиваторов. Резервирование данных
Источник: vunivere.ru