На этом уроке мы напишем программу на си для решения уравнения перебором Ищем решение уравнения в целых числах методом полного перебора При написании программы полезным бует урок Циклы в Си.Описание алгоритм программы решения уранения методом перебора.В программе вводится функция, которая определяет левую часть уравнения.Подробно о функции в Си
// задаем уравнение
int ur(int x, int y)
Задается диапазон для обоих переменных,в котором будет производиться поиск решения. Диапазон задается с клавиатуры. Подробно о вводе информации в Си с клавиатуры
printf («Задайте диапазон поискаn»);
printf(«Левая границаn»);
scanf(«%d»,
printf(«Правая границаn»);
scanf(«%d»,
Чтобы перебрать все значения переменных используются вложенные циклы for . Первый цикл отвечает за перебор для переменной x, второй вложенный цикл для переменной y.
// пробегаем все возможные x
for (i=a;i
Задание 27 (Подпоследовательности) // ЕГЭ по информатике 2022
Пример полного решения программа на си решение уравнения перебором
//решение уравнения в целых числах с двумя переменными
#include
#include
#include
// задаем уравнение
int ur(int x, int y)
int main()
Название или описание блога (изменить)
Навигация
Звонки
Новое в блогах
10 класс. П.70 Практическая работа №61. Решение уравнений методом перебора
Учебник. К.Ю Поляков, Е.А. Ерёмин. Информатика. 10 класс. Углублённый уровень. §70 Решение уравнений
Практическая работа №61. Решение уравнений методом перебора
Напишите программу, которая находит все решения заданного вам уравнения на интервале [-5;5]. Программа должна выполнить следующие действия:
1. Определяет и выводит на экран интервалы, на которых расположены корни уравнения.
2. На каждом интервале, используя метод перебора, ищет решение с точностью 0,001 и выводит полученные решения на экран.
Вычисление функции, стоящей в левой части уравнения, оформите в виде подпрограммы.
Уровень A. Интервалы, на которых расположены корни, можно найти с помощью электронных таблиц. Программа запрашивает левую границу очередного интервала и выводит найденный корень уравнения.
Введите левую границу интервала:
Уровень B. Составить две программы, одна из которых выделяет все интервалы, на которых находятся корни, а вторая запрашивает левую границу очередного интервала и выводит найденный корень уравнения.
Уровень C. Составить одну программу, которая работает полностью автоматически: достаточно ввести в программу функцию и запустить. Программа находит все интервалы, на которых расположены корни и уточняет решения. После того, как очередной интервал найден, программа выводит его на экран и, применяя метод перебора с нужным шагом, уточняет решение.
Интервал [- 2;- 1 , 5]
Вариант 1. x 3 — 8*x + 1 = sin(x)
program pr61ABC;
function f(x: real): real;
begin
f := x * x * x — 8 * x + 1 — 5 * sin(x);
end ;
const
var
begin
writeln(‘Введите левую границу интервала:’);
while (f(x) * f(x + delta) > 0) and (k
if k
then writeln(‘x = ‘, (x + eps):6:3)
else writeln(‘Возможно корни находятся левее введённой границы’);
while a
begin
while (f(a) * f(a + 0.1) > 0) and (a
if (f(a) * f(a + 0.1)
then begin
writeln(‘Интервал [‘, a, ‘;’, a + 0.1, ‘]’);
while f(x) * f(x + delta) > 0 do x := x + delta;
writeln(‘Решение: ‘, (x + eps):6:3)
end;
end;
end .
using namespace std;
double f(double x)
return x * x * x — 8 * x + 1 — 5 * sin(x);
double eps = 0.001;
double x, delta, a;
while ((f(x) * f(x + delta) > 0) (k
else cout Возможно корни находятся левее введённой границы»
while (a
while ((f(a) * f(a + 0.1) > 0) (a
if (f(a) * f(a + 0.1)
while ( f(x) * f(x + delta) > 0 ) x += delta;
ЕГЭ по информатике 2022 — Задание 6 (Метод перебора)
Сегодня посмотрим 6 задание из ЕГЭ по информатике 2022.
В этом уроке мы будем использовать метод перебора для решения различных задач из 6 задания ЕГЭ по информатике 2022.
Решать задачи будем на языке Python.
Определите, при каком наименьшем введённом значении переменной s программа выведет число 23. Для Вашего удобства программа представлена на трёх языках программирования.
Источник задачи: https://kpolyakov.spb.ru/
Решим задачу с помощью перебора.
Будем подставлять каждое число в диапазоне от 1 до 1000 в наш алгоритм с помощью цикла for. Узнаем, при каких значениях на выходе программа будет печатать число 23.
Вместо команды input() присваиваем в переменную n очередное число. В конце программы вместо команды print() пишем условие. Печатаем только те значения переменной i, которые приводят к тому, что в переменной n будет нужный результат (число 23).
Программа напечатает следующие числа:
Самое маленькое число, которое подходит, это 256.
Ещё одна задача-ловушка из 6 задания ЕГЭ по информатике 2022.
Определите, сколько существует целых положительных значений, подаваемых на вход программе, при которых программа выведет 27.
В этой программе подвох заключается в том, что, если мы будем перебирать числа от 1 до 1000, то программа зависнет и ничего не напечатает.
В таких случаях можно попробовать перебрать числа с 1000 до 1.
Третий параметр «-1» для цикла for означает, что мы перебираем числа с 1000 до 1 в обратном порядке.
Программа напечатает числа с 80 до 27.
Если проверить на небольших числа, то мы должны прибавить 1 к разнице двух чисел.
Закрепим метод перебора в 6 задании из ЕГЭ по информатике 2022.
(А.Г. Минак) Определите, при каком введённом значении переменной s программа выведет число 16.
Источник задачи: https://kpolyakov.spb.ru/
Здесь справляется стандартный перебор от 1 до 1000.
Источник: al-shell.ru
Входные и выходные данные.
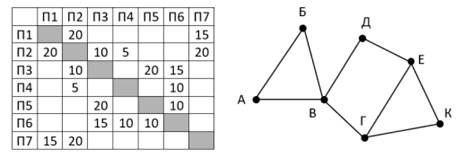
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину кратчайшего пути между пунктами В и К. Передвигаться можно только по указанным дорогам.
Задание 2
Логическая функция F задаётся выражением
((x → z) ∧ (z → w)) ∨ (y ≡ (x ∨ z)).
На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
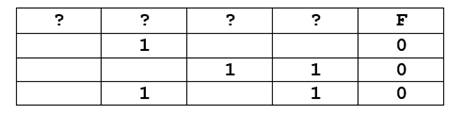
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Задание 3
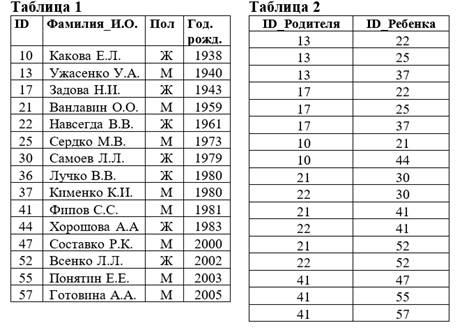
В фрагменте базы данных представлены сведения о родственных отношениях. На основании приведённых данных определите сколько племянников и племянниц старше хотя бы одного из своих дядей или хотя бы одной из своих тетей (дядя или тетя — это родные брат или сестра матери или отца).
Задание 4
Для кодирования некоторой последовательности, состоящей из букв Л, М, Н, П, Р, решили использовать неравномерный двоичный код, удовлетворяющий условию, что никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Для букв Л, М, Н использовали соответственно кодовые слова 00, 01, 11.
Для двух оставшихся букв – П и Р – кодовые слова неизвестны. Укажите кратчайшее возможное кодовое слово для буквы П, при котором код будет удовлетворять указанному условию. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Задание 5
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописывается (дублируется) последняя цифра.
3) Затем справа дописывается 0, если в двоичном коде числа N чётное число единиц, и 1, если нечётное.
4) К полученному результату дописывается ещё один бит чётности так, чтобы количество единиц в двоичной записи полученного числа стало чётным.
Полученная таким образом запись (в ней на три разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите минимальное число R, большее 105, которое могло получиться в результате работы автомата. В ответе это число запишите в десятичной системе.
Задание 6
Определите, сколько существует целых положительных значений, подаваемых на вход программе, при которых программа выведет 80.

Задание 7 (№140).
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 1024 на 512 пикселей при условии, что в изображении могут использоваться 64 различных цвета? В ответе запишите только целое число, единицу измерения писать не нужно.
Задание 8
Алексей составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Алексей использует 5-буквенные слова, в которых есть только буквы A, B, C, X, причём буква X может появиться на последнем месте или не появиться вовсе. Сколько различных кодовых слов может использовать Алексей?
Задание 9
В файле электронной таблицы содержатся вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Найдите среднее значение измерений в апреле во второй половине дня (с 12:00), в которых температура не превышала 19 градусов.
В ответе запишите только целую часть получившегося числа.
Задание 10
С помощью текстового редактора определите, сколько раз, встречается слово «футляр» или «Футляр» в тексте рассказа А.П. Чехова «Человек в футляре». Другие формы слова «футляр», такие как «футляры», «футляре» и т.д., учитывать не следует. В ответе укажите только число.
Задание 11
Задание 12
Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (1111)
Заменить (1111, 7)
Заменить (77, 1)
КОНЕЦ ПОКА
КОНЕЦ
Какая строка получится в результате применения приведённой программы к строке вида 1…17…7 (95 единиц и 31 семёрка)?
Задание 13
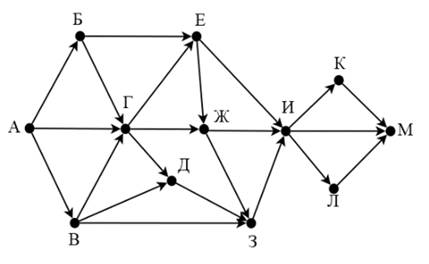
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует маршрутов длиной 8 из пункта А в пункт М? Длиной пути считать количество дорог, составляющих этот путь.
Задание 14
Значение выражения 7 202 + 49 102 — 7 20 записали в семеричной системе счисления. Сколько цифр 6 в такой записи?
Задание 15
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».
Для какого наибольшего натурального числа А формула
ДЕЛ(x, А) → (ДЕЛ(x, 6) → ДЕЛ(x, 9))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Задание 16
Алгоритм вычисления функции F(n) задан следующими соотношениями:
F(n) = F(n – 1) + 3*F(n – 3) + 2, при n > 10,
F(n) = -F(n – 1) для остальных случаев.
Чему равно значение функции F(20)?
Задание 17
Рассматривается множество целых чисел, принадлежащих числовому отрезку [8800; 55535], которые удовлетворяют следующим условиям:
− произведение разрядов больше 35;
− один из разрядов равен 7.
Найдите наибольшее из таких чисел и их количество.
Для выполнения этого задания можно написать программу или воспользоваться редактором электронных таблиц.
Задание 18
Нам важно, чтобы Дружище съел как можно меньше конфет и при этом добрался из левой верхней клетки в правую нижнюю.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
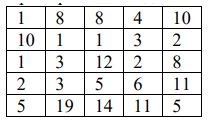
Для указанных входных данных ответом должно быть число – минимально возможное съедаемое количество конфет – 53.
Задание 19
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
а) добавить в кучу один камень;
б) увеличить количество камней в куче в два раза;
в) увеличить количество камней в куче в три раза.
Игра завершается в тот момент, когда количество камней в куче становится не менее 36. Если при этом в куче оказалось не более 60 камней, то победителем считается игрок, сделавший последний ход. В противном случае победителем становится его противник. В начальный момент в куче было S камней, 1 ≤ S ≤ 35.
Найдите минимальное значение S, при котором Ваня выигрывает своим первым ходом при любой игре Пети.
Задание 20.
Для игры, описанной в задании 19, определите сколько существует значений S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Задание 21.
Для игры, описанной в задании 19, найдите минимальное и максимальное значения S, при которых одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Найденные значения запишите в ответе в порядке возрастания.
Задание 22
Ниже записана программа. Получив на вход число x, эта программа печатает два числа, L и M. Укажите наибольшее из таких чисел x, при вводе которых алгоритм печатает сначала 4, а потом 8.

Задание 23
У исполнителя Калькулятор три команды, которым присвоены номера:
3. возведи в квадрат
Сколько есть программ, которые число 5 преобразуют в число 154?
Задание 24 (№505).
Текстовый файл состоит не более чем из 10 6 десятичных цифр. Найдите максимальную длину последовательности, каждые две соседние цифры в которой в сумме дают значение не меньшее 10.
Например, в последовательности 1567543853 есть две такие последовательности 5675 и 385.
В качестве ответа укажите максимальную длину найденной последовательности.
Для выполнения этого задания следует написать программу.
Задание 25
Уникальным назовём число, если у него первые две цифры нечётные. Для интервала [33333;55555] найдите числа, которые делятся на 7, 11, 13. В качестве ответа приведите пары чисел – порядковый номер по возрастанию найденного числа и само число.
Задание 26
Каждый день Петр ест некоторое количество конфет. Так как Петр любит фантики от конфет, то он каждый такой фантик откладывает. Таким образом каждый день у него набирается некоторое количество фантиков.
Нашему герою интересно, какое максимальное количество фантиков он сможет собрать за K дней (необязательно идущих подряд) и минимальное количество фантиков, собранных за день. Помогите нашему герою узнать эту информацию.
Входные и выходные данные.
В первой строке входного файла находятся два числа: N – Общее количество дней, на протяжении которых Петр собирал фантики (натуральное число, не превышающее 10 000) и K – количество дней, на протяжении которых Петр собрал максимально возможное количество фантиков (натуральное число, не превышающее 1000).
В следующих N строках находятся значения количества собранных фантиков (все числа натуральные, не превышающие 100), каждое в отдельной строке.
Гарантируется, что N > K.
Запишите в ответе два числа: максимальное число фантиков, собранных Петей за K дней и минимальное количество собранных главным героем за один день
Пример входного файла:
При таких исходных данных Петр может собрать суммарно максимум 150 фантиков за 3 дня (40+50+60 = 150)
Наименьшие количество собранных главным героем фантиков за один день оказалось – 10
Задание 27
Дан набор данных, состоящий из неотрицательных целых чисел. Из данного набора выбрали пары четных элементов, между которыми находится четное количество единиц (не меньше 2). Программа должна напечатать одно число – количество пар, которые удовлетворяет условию выбора.
Даны два входных файла: файл A и файл B, каждый из которых содержит в первой строке количество чисел N (1 ≤ N ≤ 100000). Каждая из следующих N строк содержит одно целое положительное число.
Пример входного файла:
Для указанных входных данных количество пар с четными значениями 2 – (8, 6), (2, 6).
В ответе укажите два числа: сначала количество троек для файла А, затем для файла B.
Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.
Источник: poisk-ru.ru
Информатика 11 класс пробный вариант №3 ЕГЭ 2022 задания с ответами
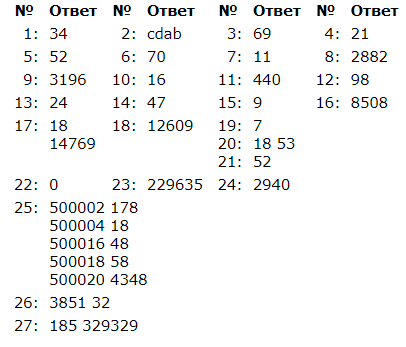

1)На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице числами обозначены длины дорог в километрах. Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Найдите номера пунктов в таблице, соответствующие пунктам А и В на схеме, если известно, что дорога между А и В длиной 10 километров. В качестве ответа запишите без разделителей два числа – номера пунктов в таблице, соответствующие пунктам А и В на схеме, в порядке возрастания.
Ответ: 34
2)Логическая функция F задаётся выражением (a → b) ∧ ¬(b ≡ c) ∧ (d → a). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся наборы аргументов, при которых функция F истинна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d. В ответе напишите буквы a, b, c, d в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Ответ: cdab
Ответ: 69
4)По каналу связи передается сообщение «ПИРАНЬЯ». Для передачи используется двоичный код, допускающий однозначное декодирование. Укажите минимально возможную длину закодированной последовательности, если известно, что в сообщении могут встречаться и другие буквы, кроме тех, которых входят в передаваемое слово.
Ответ: 21
Ответ: 52
6)Определите, сколько существует целых положительных значений, подаваемых на вход программе, при которых программа выведет 80. s = int(input()) n = 10 while s — n < 1000: s = s + n n = n + 5 print(n)
Ответ: 70
7)Найдите битовую глубину кодирования растрового изображения размером 2048×8 пикселей, которое занимает 22 Кбайт? В ответе запишите только целое число, единицу измерения писать не нужно.
Ответ: 11
8)Стасик выписывает все пятисимвольные комбинации, составленные из букв Ш, К, О, Л, А. При этом упорядочивая их по алфавиту. Вот начало списка: 1. ААААА 2. ААААК 3. ААААЛ 4. ААААО 5. ААААШ … Определите, сколько слов хотя бы с одной гласной напишет Стасик.
Ответ: 2882
Ответ: 3196
Ответ: 16
Ответ: 440
12)Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки символов. 1. заменить (v, w) 2. нашлось (v) Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Если цепочки v в строке нет, эта команда не изменяет строку. Вторая команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Дана программа для исполнителя Редактор: ПОКА нашлось(43) ИЛИ нашлось(53) ЕСЛИ нашлось(43) ТО заменить(43, 33) ИНАЧЕ заменить(53, 433) КОНЕЦ ПОКА Определите максимально возможное количество цифр 3, которое может получиться в результате применения этой программы к строке, состоящей из 17 цифр 3, 23 цифр 4 и 29 цифр 5, идущих в произвольном порядке.
Ответ: 98
13)На рисунке – схема дорог, связывающих пункты A, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует круговых маршрутов из А в А? Пустой маршрут без движения из пункта А не считать.
Ответ: 24
14)Значение выражения 16 44 • 16 30 – (32 5 • (8 40 – 8 32 ) • (16 17 – 32 4 )) записали в системе счисления с основанием 16. Затем в шестнадцатеричной записи этого числа все цифры F заменили на 0, а цифры в разрядах 0, 1 и 2 удалили. Найдите количество значащих нулей в шестнадцатеричной записи числа после изменения. Ответ запишите в десятичной системе счисления.
Ответ: 47
15)На числовой прямой даны два отрезка: P=[5,30] и Q=[14,23]. Укажите наибольшую возможную длину такого отрезка A, что формула ((x ∈ P) ≡ (x ∈ Q)) → (x ∉ A) тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
Ответ: 9
16)Алгоритм вычисления значения функции F(n), где n – целое число, задан следующими соотношениями: F(n) = n + 3, при n ≤ 3 F(n) = F(n – 2) + n, при n > 3 и четном значении F(n-1), F(n) = F(n – 2) + 2•n, при n > 3 и нечетном значении F(n-1). Определите сумму значений, являющихся результатом вызова функции для значений n в диапазоне [40; 50].
Ответ: 8508
17)В файле 17-202.txt содержится последовательность целых чисел, которые принимают значения от -10000 до 10000 включительно. Тройка идущих подряд чисел последовательности называется уникальной, если только второе из них является положительным трёхзначным числом, заканчивающимся на 5. Определите количество уникальных троек чисел, а затем – максимальную из всех сумм таких троек.
Ответ: 18, 14769
Ответ: 12609
19)Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может а) добавить в кучу один камень; б) увеличить количество камней в куче в три раза. Игра завершается в тот момент, когда количество камней в куче становится не менее 56.
Если при этом в куче оказалось не более 80 камней, то победителем считается игрок, сделавший последний ход. В противном случае победителем становится его противник. В начальный момент в куче было S камней, 1 ≤ S ≤ 55. Ответьте на следующие вопросы: Вопрос 1. Известно, что Ваня выиграл своим первым ходом после первого хода Пети. Назовите мини-мальное значение S, при котором это возможно.
Вопрос 2. Определите, два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия: − Петя не может выиграть за один ход; − Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания. Вопрос 3. Найдите значение S, при которых одновременно выполняются два условия: – у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети; – у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
22)Получив на вход натуральное число x, этот алгоритм печатает два числа: a и b. Сколько существует натуральных чисел, цифры в которых расположены в порядке невозрастания, при вводе которых алгоритм печатает сначала 9, а потом 5.
23)Исполнитель Калькулятор преобразует число, записанное на экране. У исполнителя есть три команды, которым присвоены номера: 1. Прибавь 1 2. Умножь на 2 3. Сделай нечётное Первая команда увеличивает число на 1, вторая – вдвое, третья прибавляет к четному числу 1, к нечетному – 2. Сколько существует таких программ, которые исходное число 3 преобразуют в число 25 и при этом траектория вычислений программы содержит число 9 и число 17?
24)Текстовый файл 24-157.txt состоит не более чем из 10 6 символов и содержит только заглавные буквы латинского алфавита (A..Z). Определите максимальное количество идущих подряд символов, среди которых нет сочетания стоящих рядом букв P и R (в любом порядке).
25)Найдите 5 чисел больших 500000, таких, что среди их делителей есть число, оканчивающееся на 8, при этом этот делитель не равен 8 и самому числу. В качестве ответа приведите 5 наименьших чисел, соответствующих условию. Формат вывода: для каждого из найденных чисел в отдельной строке запишите само число, а затем минимальный делитель, оканчивающийся на 8, не равный 8 и самому числу.
26)Администратор написал скрипт для раскладки N архивов на K дисков, каждый объемом V. Алгоритм скрипта обрабатывает файлы в порядке убывания их размера. Если файл помещается на диск, то следующий по размеру файл стараются поместить на следующий диск. Если не помещается, то на следующий, и так по кругу. Если файл не поместился ни на один диск, то он откладывается в локальную папку.
Укажите в ответе два числа: объем всех отложенных файлов и их количество. Входные данные представлены в файле 26-56.txt следующим образом. В первой строке входного файла записаны значения V (объём диска), K (количество дисков) и N (количество архивов). Каждая из следующих N строк содержит одно целое число – размер очередного архива. В ответе запишите два числа – объем всех отложенных файлов и их количество.
27)Дана последовательность из N натуральных чисел. Рассматриваются все её непрерывные подпоследовательности, такие что сумма элементов каждой из них кратна k = 43. Найдите среди них подпоследовательность с максимальной суммой, определите её длину. Если таких под последовательностей найдено несколько, в ответе укажите количество элементов самой короткой из них. Входные данные.
Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество чисел N (2 ≤ N ≤ 10 8 ). Каждая из следующих N строк содержит натуральное число, не превышающее 10000.
Источник: 100ballnik.com