Информатика 11 класс пробный вариант №6 решу ЕГЭ 2022 задания с ответами

1)На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице приведены длины дорог между пунктами. Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину кратчайшего пути из пункта Б в пункт Е, если передвигаться можно только по указанным дорогам. В ответе запишите целое число – длину пути в километрах.
Правильный ответ: 20
2)Логическая функция F задаётся выражением (x ≡ y) → (z ≡ w). Ниже приведён частично заполненный фрагмент таблицы истинности этой функции, содержащий неповторяющиеся строки. Сколькими способами можно поставить в соответствие переменные w, x, y, z столбцам таблицы истинности функции F, опираясь на информацию из данного фрагмента? Пример. Функция F задана выражением x ∨ y ∨ z, а фрагмент таблицы истинности имеет вид: в этом случае переменные можно расставить любым способом, значит, ответом будет число 6.
ЕГЭ 2023 1-й день 19.06.23 Задачи 1 — 27 | ЕГЭ 2023 Информатика
Правильный ответ: 12
Правильный ответ: CHINA
4)По каналу связи передаются сообщения, содержащие только семь букв: О, К, Т, Я, Б, Р, Ь. Для передачи используется двоичный код, допускающий однозначное декодирование. Кодовые слова для некоторых букв известны: К – 1010, Т – 100, Б – 0101, Р – 110, Ь – 001. Укажите минимальную возможную сумму длин кодов всех букв.
Правильный ответ: 22
Правильный ответ:103
6)Определите наибольшее введённое значение переменной n, при котором программа выведет число 45.
Правильный ответ: 99
7)Каким может быть максимальное количество цветов в палитре, чтобы растровое изображение размером 512х415 пикселей можно было сохранить, используя 256 Кбайт памяти? В ответе запишите только целое число, единицу измерения писать не нужно.
Правильный ответ: 512
8)Петя составляет список из 5-буквенных слов, в состав которых входят только буквы А, О, У. Петя расположил слова в обратном алфавитном порядке. Вот начало списка: 1. УУУУУ 2. УУУУО 3. УУУУА 4. УУУОУ … Запишите слово, которое стоит в этом списке под номером 100.
Правильный ответ: ОУАУУ
Правильный ответ: 1114
Правильный ответ: 44
12)Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки символов. 1. заменить (v, w) 2. нашлось (v) Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Если цепочки v в строке нет, эта команда не изменяет строку.
Вторая команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Дана программа для исполнителя Редактор: НАЧАЛО ПОКА нашлось(01) ИЛИ нашлось(02) ИЛИ нашлось(03) заменить(01, 30) заменить(02, 3103) заменить(03, 1201) КОНЕЦ ПОКА КОНЕЦ Известно, что исходная строка начиналась с нуля, а далее содержала только единицы, двойки и тройки. После выполнения данной программы получилась строка, содержащая 59 единиц, 40 двоек и 66 троек. Сколько единиц было в исходной строке?
Разбор 6 задания | ОГЭ по информатике 2023
Правильный ответ: 7
13)На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько маршрутов идет из В в Ж?
Правильный ответ: 5
14) Значение выражения (7 160 • 7 90 ) – (14 150 + 2 13 ) записали в системе счисления с основанием 7. Найдите сумму всех цифр семеричной записи числа, исключая шестерки.
Правильный ответ: 145
15)На числовой прямой даны два отрезка: P=[35,55] и Q=[45,65]. Определите наименьшую возможную длину отрезка A, при котором формулы (x ∈ P) → (x ∈ А) (x ∉ A) → (x ∉ Q) тождественно истинны, то есть принимают значение 1 при любом значении переменной х.
Правильный ответ: 30
16)Алгоритм вычисления значения функции F(n), где n – целое число, задан следующими соотношениями: F(0) = 0 F(n) = F(n/2), при чётном n > 0 F(n) = F(n — 1) + 3, при нечётном n > 0 Сколько существует значений n, принадлежащих отрезку [1; 1000], для которых F(n) равно 18?
Правильный ответ: 209
17)В файле 17-199.txt содержится последовательность целых чисел, которые принимают значения от -10000 до 10000 включительно. Тройка идущих подряд чисел последовательности называется уникальной, если только второе из них является положительным двузначным чётным числом. Определите количество уникальных троек чисел, а затем – максимальную из всех сумм таких троек.
Правильный ответ: 7, 12441
Правильный ответ: 137, 7
19-21)Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может а) добавить в кучу один камень; б) увеличить количество камней в куче в два раза. Игра завершается в тот момент, когда количество камней в куче становится не менее 25.
Если при этом в куче оказалось не более 45 камней, то победителем считается игрок, сделавший последний ход. В противном случае победителем становится его противник. В начальный момент в куче было S камней, 1 ≤ S ≤ 24. Ответьте на следующие вопросы: Вопрос 1. Известно, что Ваня выиграл своим первым ходом после первого хода Пети. Назовите минимальное значение S, при котором это возможно.
Вопрос 2. Определите, два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия: − Петя не может выиграть за один ход; − Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания. Вопрос 3. Найдите значение S, при которых одновременно выполняются два условия: – у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети; – у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
22)Ниже записана программа, которая вводит натуральное число x, выполняет преобразования, а затем выводит результат. Укажите наименьшее значение x, при вводе которого программа выведет число 96.
Правильный ответ: 411
23)Исполнитель Калькулятор преобразует число, записанное на экране в троичной системе счисления. У исполнителя есть две команды, которым присвоены номера: 1. Прибавь 3 2. Умножь на 2 и прибавь 1 Сколько различных результатов можно получить из исходного числа 2 после выполнения программы, содержащей ровно 13 команд?
Правильный ответ: 973
24)Текстовый файл 24-174.txt состоит не более чем из 10 6 символов и содержит только заглавные буквы латинского алфавита (ABC…Z). Файл разбит на строки различной длины. Замкнутой цепочкой называется подстрока (часть одной строки файла) длиной не менее трёх символов, которая начинается и заканчивается на одну и ту же букву, но внутри этих букв не содержит.
Нужно определите длину самой длинной замкнутой цепочки в строках, содержащих менее 30 букв R, а также общее количество замкнутых цепочек во всех таких строках. Пример. Исходный файл PRIVET INFORMATIKA AWERTYUIOPAZXCA В этом примере во всех строках меньше 30 букв R. В третьей строке повторяются буквы А с порядковыми номерами 1, 11, 15. Самое большое расстояние будет между позициями 1 и 11. В ответе для данного примера нужно вывести число 10 (наибольшее расстояние) и 4 (число замкнутых цепочек: INFORMATI, ATIKA, AWERTYUIOPA, AZXCA).
25)Пифагоровой тройка назовём тройку чисел (a, b, c), такую что a ≤ b ≤ с и a2+b 2=c2 . Найдите все пифагоровы тройки, в которых все числа находятся в диапазоне [1; 5000]. Запишите в ответе количество подходящих троек, а затем – значение c для тройки, в которой сумма a+b+c максимальна.
26)В текстовом файле записан набор натуральных чисел. Гарантируется, что все числа различны. Необходимо определить, сколько в наборе таких пар нечётных чисел, что их среднее арифметическое тоже присутствует в файле, и чему равно наибольшее из средних арифметических таких пар. Входные данные представлены в файле 26-53.txt следующим образом.
Первая строка содержит целое число N – общее количество чисел в наборе. Каждая из следующих N строк содержит одно число, не превышающее 10 9 . В ответе запишите два целых числа: сначала количество пар, затем наибольшее среднее арифметическое.
27)Набор данных представляет собой последовательность натуральных чисел. Необходимо найти количество подпоследовательностей подряд идущих чисел, сумма которых делится на 71. Гарантируется, что такие подпоследовательности существуют. Входные данные. Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество чисел N (2 ≤ N ≤ 10 8 ). Каждая из следующих N строк содержит натуральное число, не превышающее 10000.
Источник: 100ballnik.com
Подготовка к ЕГЭ Информатика. Задание 16






 «ИНФОРМАТИКА» 11 КЛАС С
«ИНФОРМАТИКА» 11 КЛАС С
Рабочая тетрадь
РАЗДЕЛ: Программирование
ТЕМА: Решение задач 16 ЕГЭ
Ворона Елена Дмитриевна,

Задачи для самостоятельного решения
Рекурсия. Рекурсивные процедуры и функции
16.1 Простая:
(П1) Алгоритм вычисления функции F( n ) задан следующими соотношениями:
F ( n ) = 1 при n = 1
F ( n ) = 2· F ( n – 1) + n + 3, если n > 1
Чему равно значение функции F(19)?
(П9) Алгоритм вычисления функции F( n ) задан следующими соотношениями:
F ( n ) = n – 3 при n > 16
F ( n ) = 2· F ( n +1) + 2 n + 3, если n £ 16
Чему равно значение функции F(2)?
16.2 Четность:
(П11) Алгоритм вычисления функции F( n ) задан следующими соотношениями:
F ( n ) = 1 при n = 1
F ( n ) = 2· F ( n – 1), если n чётно,
F ( n ) = 5 n + F ( n – 2), если n нечётно.
Чему равно значение функции F(64)?
(П13) Алгоритм вычисления функции F( n ) задан следующими соотношениями:
F ( n ) = 2· n при n < 3
F ( n ) = 3 n + 5 + F ( n – 2), если n чётно,
F ( n ) = n + 2· F ( n – 6), если n нечётно.
Чему равно значение функции F(61)?
(П14) Алгоритм вычисления функции F( n ) задан следующими соотношениями:
F ( n ) = – n при n < 0
F ( n ) = 2 n + 1 + F ( n – 3), если n чётно,
F ( n ) = 4 n + 2· F ( n – 4), если n нечётно.
Чему равно значение функции F(33)?
16.3 Кратность:
(П16) Алгоритм вычисления функции F( n ) задан следующими соотношениями:
F ( n ) = 1+2 n при n < 5
F ( n ) = 2·( n + 1)· F ( n – 2), если n делится на 3,
F ( n ) = 2· n + 1 + F ( n – 1) + 2· F ( n – 2), если n не делится на 3.
Чему равно значение функции F(15)?
(П45 Амеличев) Алгоритм вычисления функции F( n ) задан следующими соотношениями:
F(n) = n при n ≤ 3;
F(n) = n * n * n + F(n – 1), если n > 3 и дает остаток 0 при делении на 3
F(n) = 4 + F(n // 3), если n > 3 и дает остаток 1 при делении на 3
F(n) = n * n + F(n – 2), если n > 3 и дает остаток 2 при делении на 3
Здесь // обозначает деление нацело. В качестве ответа на задание выведите значение F (100).
16.4 Две функции:
(П20) Алгоритм вычисления функций F( n ) и G ( n ) задан следующими соотношениями:
F (1) = G (1) = 1
F ( n ) = 3· F ( n – 1) + G ( n – 1) – n + 5, если n > 1
G ( n ) = F ( n – 1) + 3· G ( n – 1) – 3· n , если n > 1
Чему равно значение F(14) + G(14)?
16.5 Количество (сумма) простые:
(П21) Определите, сколько символов * выведет эта процедура при вызове F(28):
(П24) Определите, сколько символов * выведет эта
процедура при вызове F(280):
(7756)(11) Чему равна сумма всех чисел, напечатанных на экране при выполнении вызова F(5)?
16.6 Мин(макс) с неизвестным числом элементов
(П26) Определите наименьшее значение n , при котором сумма чисел, которые будут выведены при вызове F( n ), будет больше 1000000. Запишите в ответе сначала найденное значение n , а затем через пробел – соответствующую сумму выведенных чисел.
(П31 Муфаззалов) Определите наименьшее значение n , при котором значение F( n ), будет больше числа 320. Запишите в ответе сначала найденное значение n , а затем через пробел – соответствующее значение F( n ).
(П32 Муфаззалов) Определите наибольшее трехзначное значение n , при котором значение F( n ), будет больше числа 7. Запишите в ответе сначала найденное значение n , а затем через пробел – соответствующее значение F( n ).
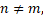
(П35 Муфаззалов) Определите наименьшее значение суммы n + m такое, что значение F( n , m ) больше числа 15 и выполняется условие n и m – натуральные числа. Запишите в ответе сначала значения n и m , при которых указанная сумма достигается, в порядке неубывания, а затем – соответствующее значение F( n , m ). Числа в ответе разделяйте пробелом.
if n != m: return F(n-m,m)
16.7 Количество чисел по условию
(П47) Алгоритм вычисления функции F( n ) задан следующими соотношениями:
F ( n ) = n при n ≤ 3;
F ( n ) = F ( n – 1) + 2 · F ( n / 2) при чётных n > 3;
F ( n ) = F ( n – 1) + F ( n – 3) при нечётных n > 3;
Определите количество натуральных значений n , при которых F ( n ) меньше, чем 10 8 .
16.8 Сумма цифр числа, без цифры (с цифрой)…
(П54) Алгоритм вычисления функции F( n ) задан следующими соотношениями:
F ( n ) = 2 · n · n · n + n · n при n > 25
F ( n ) = F ( n +2) + 2 · F ( n +3), если n £ 25
Чему равна сумма цифр значения функции F(2)?
(П56) Алгоритм вычисления функции F( n ) задан следующими соотношениями:
F (n) = n · n · n + n при n > 20
F (n) = 3 · F(n+1) + F(n+3), при чётных n £ 20
F (n) = F(n+2) + 2 · F(n+3), при нечётных n £ 20
Определите количество натуральных значений n из отрезка [1; 1000], при которых значение F ( n ) не содержит цифру 1.
(П59) Алгоритм вычисления функции F( n ) задан следующими соотношениями:
F ( n ) = n · n + 5 · n + 4, при n > 30
F ( n ) = F ( n +1) + 3 · F ( n +4), при чётных n £ 30
F ( n ) = 2 · F ( n +2) + F ( n +5), при нечётных n £ 30
Определите количество натуральных значений n из отрезка [1; 1000], для которых сумма цифр значения F ( n ) равна 27.
(П62) Алгоритм вычисления функции F( n ) задан следующими соотношениями:
F ( n ) = 2 · n · n + 4 · n + 3, при n £ 15
F ( n ) = F ( n – 1) + n · n + 3, при n > 15, кратных 3
F ( n ) = F ( n – 2) + n – 6, при n > 15, не кратных 3
Определите количество натуральных значений n из отрезка [1; 1000], для которых все цифры значения F ( n ) нечётные.
(П66) Алгоритм вычисления функции F( n ) задан следующими соотношениями:
F ( n ) = n · n + 11, при n £ 15
F ( n ) = F ( n // 2) + n · n · n – 5 · n , при чётных n > 15
F ( n ) = F ( n – 1) + 2 · n + 3, при нечётных n > 15
Здесь «//» обозначает деление нацело. Определите количество натуральных значений n из отрезка [1; 1000], для которых значения F ( n ) содержит не менее трёх цифр 6.
16.9 Что будет выведено
(10501) (4321021) Что выведет программа при вызове F(4)? В ответе запишите последовательность выведенных цифр слитно (без пробелов).
16.10 Задачи с бесконечными выражениями
(П71) (Е. Джобс) Алгоритм вычисления функции F ( n ), где n – натуральное число, задан следующими соотношениями:
F ( n ) = 5 при n = 0,
F ( n ) = 3 × F ( n – 4) , когда n > 0,
F ( n ) = F ( n + 3), когда n < 0 .
Чему равно значение F (43) ?
(81П) Алгоритм вычисления функции F ( n ), где n – натуральное число, задан следующими соотношениями:
F ( n ) = n , при n £ 5 ,
F ( n ) = n + F ( n / 5 + 1), когда n > 5 и делится на 5,
F ( n ) = n + F ( n + 6) , когда n > 5 и не делится на 5.
Назовите минимальное значение n , для которого F (n) определено и больше 1000.
(П76) Алгоритм вычисления функции F ( n ), где n – натуральное число, задан следующими соотношениями:
F ( n ) = 1, при n £ 1 ,
F ( n ) = 3 + F ( n / 2 – 1), когда n > 1 и чётное,
F ( n ) = n + F ( n + 2) , когда n > 1 и нечётное.
Назовите минимальное значение n , для которого F (n) = 19.
Источник: znanio.ru