Рабочая программа учебной дисциплины разработана на основе Федерального государственного образовательного стандарта среднего профессионального образования по специальности 09.02.07 Информационные системы и программирование и примерной программы учебной дисциплины «Численные методы».
Нураева Э.В., преподаватель
Рабочая программа учебной дисциплины рассмотрена
на заседании цикловой комиссии
Протокол № 11 от « 22 » июня 2022 г.
Председатель _________________ / Э.В. Нураева
Рассмотрено на заседании методического Совета
Протокол № __ от « __ » июня 2022 г.
Методист _____________________ Л.П. Антюфеева
1. ПАСПОРТ ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ — 4
2. СТРУКТУРА И СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ — 6
3. УСЛОВИЯ РЕАЛИЗАЦИИ ПРОГРАММЫ ДИСЦИПЛИНЫ — 9
4. КОНТРОЛЬ И ОЦЕНКА РЕЗУЛЬТАТОВ ОСВОЕНИЯ ДИСЦИПЛИНЫ — 10
1. ПАСПОРТ ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ
«Численные методы»
1.1. Область применения программы
Программа учебной дисциплины является частью основной профессиональной образовательной программы в соответствии с Федеральными государственными стандартами по специальности СПО 09.02.07 Информационные системы и программирование укрупнённой группы специальностей 09.00.00 Информатика и вычислительная техника.
10 Численные методы решения нелинейных уравнений
1.2. Место дисциплины в структуре основной профессиональной образовательной программы:
Учебная дисциплина «Численные методы» принадлежит к общепрофессиональному циклу (ОП.00)
1.3. Цели и задачи дисциплины – требования к результатам освоения дисциплины:
В результате освоения дисциплины обучающийся должен уметь:
использовать основные численные методы решения математических задач;
выбирать оптимальный численный метод для решения поставленной задачи;
давать математические характеристики точности исходной информации и оценивать точность полученного численного решения;
разрабатывать алгоритмы и программы для решения вычислительных задач, учитывая необходимую точность получаемого результата.
В результате освоения дисциплины обучающийся должен знать:
методы хранения чисел в памяти электронно-вычислительной машины (далее – ЭВМ) и действия над ними, оценку точности вычислений;
методы решения основных математических задач – интегрирования, дифференцирования, решения линейных и трансцендентных уравнений и систем уравнений с помощью ЭВМ.
Общие компетенции, которые актуализируются при изучении учебной дисциплины:
ОК 01. Выбирать способы решения задач профессиональной деятельности, применительно к различным контекстам.
ОК 02. Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельности.
ОК 04. Работать в коллективе и команде, эффективно взаимодействовать с коллегами, руководством, клиентами.
ОК 05. Осуществлять устную и письменную коммуникацию на государственном языке с учетом особенностей социального и культурного контекста.
10. Численные методы, часть 1
ОК 09. Использовать информационные технологии в профессиональной деятельности.
ОК 10. Пользоваться профессиональной документацией на государственном и иностранном языках.
Профессиональные компетенции, которые актуализируются при изучении учебной дисциплины:
ПК 1.1. Формировать алгоритмы разработки программных модулей в соответствии с техническим заданием.
ПК 1.2. Разрабатывать программные модули в соответствии с техническим заданием.
ПК 1.5. Осуществлять рефакторинг и оптимизацию программного кода.
ПК 11.1. Осуществлять сбор, обработку и анализ информации для проектирования баз данных.
1.4. Количество часов на освоение программы дисциплины:
максимальной учебной нагрузки обучающегося 62 часа, в том числе:
аудиторной учебной работы обучающегося (обязательных учебных занятий) 60 часов.
2. СТРУКТУРА И СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ
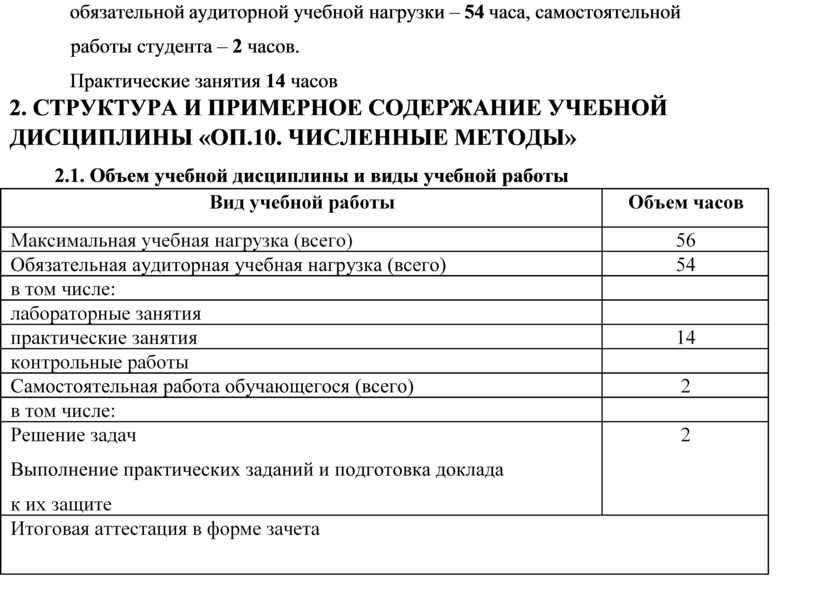
2.1. Объём учебной дисциплины и виды учебной работы
Вид учебной работы
Объём часов
Максимальная учебная нагрузка (всего)
Обязательная аудиторная учебная нагрузка во взаимодействии с преподавателем
Обязательная аудиторная учебная нагрузка без взаимодействия с преподавателем (самостоятельная работа)
Итоговая аттестация в форме дифференцированного зачёта
Наименование разделов и тем
Содержание учебного материала, лабораторные работы и практические занятия, самостоятельная работа обучающихся
Объем часов
Уровень освоения
Введение. Место теории численных методов в системе других областей знаний.
Раздел 1. Приближенные числа и действия над ними
Тема 1.1 Элементарная теория погрешностей
Содержание учебного материала
Приближенные числа и действия над ними.
Практические занятия
Вычисление погрешностей результатов арифметических действий.
Раздел 2. Численные методы
Тема 2.1 Приближенное решение алгебраических и трансцендентных уравнений
Содержание учебного материала
Уточнение корней методом половинного деления
Метод касательных для решения алгебраических и трансцендентных уравнений.
Решение уравнения методом итераций
Практические занятия
Решение трансцендентных и алгебраических уравнений методом половинного деления.
Решение уравнений методом итераций.
Тема 2.2 Решение систем линейных алгебраических уравнений
Содержание учебного материала
Методы решения систем линейных алгебраических уравнений.
Знакомство с Mathcad
Метод Гаусса при решении СЛАУ
Метод итераций при решении СЛАУ
Практические занятия
Ввод и редактирование математических выражений в Mathcad
Представление результатов вычислений в Mathcad.
Решение систем линейных уравнений методом Крамера.
Решение систем линейных уравнений методом Гаусса.
Решение систем линейных уравнений методом простой итерации.
Обязательная аудиторная учебная нагрузка без взаимодействия с преподавателем (самостоятельная работа)
История развития численных методов решения задач
Тема 2.3 Интерполирование и экстраполирование функций
Содержание учебного материала
Способы задания функций. Математические таблицы. Математическая постановка.
Задачи интерполирования. Интерполяция. Экстраполяция. Интерполяционный многочлен Лагранжа.
Квадратичное приближение табличных функций по методу наименьших квадратов
Практические занятия
Интерполирование математических таблиц.
Квадратичное приближение табличных функций по методу наименьших квадратов.
Интерполяционный многочлен Лагранжа.
Тема 2.4 Численное интегрирование
Содержание учебного материала
Приближенное вычисление определенных интегралов. Формулы прямоугольника, трапеций, правило Симпсона.
Практические занятия
Приближенное вычисление определенных интегралов.
Численное решение дифференциальных уравнений
Содержание учебного материала
Понятие о дифференциальном уравнении. Решение дифференциальных уравнений. Метод Эйлера для решения ДУ. Уточненная схема Эйлера.
Метод Рунге-Кутта для приближенного решения обыкновенных дифференциальных уравнений.
Практические занятия
Численное решение обыкновенных дифференциальных уравнений при помощи формул Эйлера-Коши.
Численное решение обыкновенных дифференциальных уравнений методом Рунге-Кутта.
Дифференцированный зачёт
3. УСЛОВИЯ РЕАЛИЗАЦИИ ПРОГРАММЫ ДИСЦИПЛИНЫ
«Численные методы»
3.1. Требования к минимальному материально-техническому обеспечению
Реализация программы дисциплины требует наличие кабинета «Математических дисциплин».
Оборудование учебного кабинета:
посадочные места по количеству обучающихся;
рабочее место преподавателя;
печатные демонстрационные пособия.
Технические средства обучения:
компьютеры, лицензионное программное обеспечение;
Информационное обеспечение обучения
Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы.
Основная литература:
1.Слабнов, В. Д. Численные методы и программирование : учебное пособие для спо / В. Д. Слабнов. — 2-е изд., стер. — Санкт-Петербург : Лань, 2022. — 460 с. — ISBN 978-5-8114-9250-3. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/189402
(дата обращения: 28.03.2022). — Режим доступа: для авториз. пользователей.
——————————————————————
2. Фомина, А. В. Численные методы : учебное пособие / А. В. Фомина. — Новокузнецк : НФИ КемГУ, 2018. — 107 с. — ISBN 978-5-8353-2001-1. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/169558
(дата обращения: 28.03.2022). — Режим доступа: для авториз. пользователей.
3. Лапчик М.П. , Рагулина М.И. , Хеннер Е. К. Численные методы. Учебник, -М.: Издательский центр «Академия», 2018. — 384с.
Дополнительная литература:
1. Олегин, И. П. Введение в численные методы : учебное пособие / И. П. Олегин, Д. А. Красноруцкий. — Новосибирск : НГТУ, 2018. — 115 с. — ISBN 978-5-7782-3632-5. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook.com/book/118322
(дата обращения: 28.03.2022). — Режим доступа: для авториз. пользователей.
4. КОНТРОЛЬ И ОЦЕНКА РЕЗУЛЬТАТОВ ОСВОЕНИЯ ДИСЦИПЛИНЫ
«Численные методы»
Контроль и оценка результатов освоения дисциплины осуществляется преподавателем в процессе проведения практических занятий и приема нормативов, а также сдачи обучающимися дифференцированного зачета.
Результаты обучения
(освоенные умения, усвоенные знания)
Основные показатели оценки результата
Умения:
использовать основные численные методы решения математических задач
владение навыками выполнения расчетов с использованием формул и стандартных функций
выбирать оптимальный численный метод для решения поставленной задачи
сформированное представление об оптимальных методах решения задач
давать математические характеристики точности исходной информации и оценивать точность полученного численного решения
владение навыками вычисления погрешностей результатов арифметических действий, определения количества верных цифр в числе
разрабатывать алгоритмы и программы для решения вычислительных задач, учитывая необходимую точность получаемого результата
владение компьютерными средствами представления и анализа данных, использование готовых компьютерных программ для поиска путей решения и иллюстрации решения уравнений и неравенств
Знания:
методы хранения чисел в памяти электронно-вычислительной машины (далее – ЭВМ) и действия над ними, оценку точности вычислений
использование готовых прикладных компьютерных программ,
понятие о методах хранения чисел в памяти, умений работать с ними
методы решения основных математических задач – интегрирования, дифференцирования, решения линейных и трансцендентных уравнений и систем уравнений с помощью ЭВМ
владение основными понятиями дифференциального и интегрального исчисления
Источник: intolimp.org
РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ «ОП.10 ЧИСЛЕННЫЕ МЕТОДЫ»


ПК 1.1. Формировать алгоритмы разработки программных модулей в соответствии с техническим заданием. ПК 1.2. Разрабатывать программные модули в соответствии с техническим заданием. ПК 1.5. Осуществлять рефакторинг и оптимизацию программного кода. ПК 3.4.
Проводить сравнительный анализ программных продуктов и средств разработки, с целью выявления наилучшего решения согласно критериям, определенным техническим заданием. ПК 5.1. Собирать исходные данные для разработки проектной документации на информационную систему. ПК 9.2. Разрабатывать веб-приложение в соответствии с техническим заданием. ПК 10.1.
Обрабатывать статический и динамический информационный контент. ПК 11.1. Осуществлять сбор, обработку и анализ информации для проектирования баз данных.
Картинками
Министерство общего и профессионального образования Свердловской области
Государственное автономное профессиональное образовательное учреждение
«КАМЕНСК-УРАЛЬСКИЙ АГРОПРОМЫШЛЕННЫЙ ТЕХНИКУМ»
Директор ГАПОУ СО
«Каменск-Уральский агропромышленный техникум»
С.И. Некрасов /__________________/ «____»__________201__ г.
Номер регистрации __________________
РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
«ОП.10 ЧИСЛЕННЫЕ МЕТОДЫ»
Для подготовки специалистов среднего звена:
09.02.03 «Программирование в компьютерных системах» Форма обучения: очная Срок обучения: 3 г. 10 мес.
Уровень освоения: базовый
Рабочая программа учебной дисциплины разработана на основе Федерального государственного образовательного стандарта по специальности среднего профессионального образования 09.02.03 Программирование в компьютерных системах (утвержден Приказом Министерства образования и науки Российской Федерации от
28.07.2014 N 804. Зарегистрировано в Минюсте России 21.08.2014 N 33733 ).
Организация-разработчик: государственное автономное профессиональное образовательное учреждение Свердловской области «Каменск-Уральский агропромышленный техникум».
2. СТРУКТУРА И ПРИМЕРНОЕ СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ«ОП.10. ЧИСЛЕННЫЕ МЕТОДЫ». 6
3. УСЛОВИЯ РЕАЛИЗАЦИИ ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ «ОП.10.ЧИСЛЕННЫЕ МЕТОДЫ». 9
4. КОНТРОЛЬ И ОЦЕНКА РЕЗУЛЬТАТОВ ОСВОЕНИЯ УЧЕБНОЙ ДИСЦИПЛИНЫ«ОП.10. ЧИСЛЕННЫЕ МЕТОДЫ». 12
Кондрашова Юлия Владимировна, преподаватель информатики и ИКТ, первая квалификационная категория
Согласовано на заседании П(Ц)К, протокол №___, от «___» ___________ 201__г.
Председатель _____________ / __________________ Согласовано на заседании НМС, протокол №___, от «____» ___________ 201__г.
Председатель _____________ / __________________
1. ПАСПОРТ ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ «ОП.10. ЧИСЛЕННЫЕ
1. ПАСПОРТ ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ «ОП.10.
ЧИСЛЕННЫЕ МЕТОДЫ»
1.1. Область применения программы
Программа учебной дисциплины является частью основной профессиональной образовательной программы профессиональной подготовки по специальности 09.02.03 Программирование в компьютерных системах в части изучения общепрофессиональных дисциплин и освоения общих и профессиональных компетенций:
ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности.
ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности.
ОК 10. Пользоваться профессиональной документацией на государственном и иностранном языке.
ПК 1.1. Формировать алгоритмы разработки программных модулей в соответствии с техническим заданием.
ПК 1.2. Разрабатывать программные модули в соответствии с техническим заданием.
ПК 1.5. Осуществлять рефакторинг и оптимизацию программного кода.
ПК 3.4. Проводить сравнительный анализ программных продуктов и средств разработки, с целью выявления наилучшего решения согласно критериям, определенным техническим заданием.
ПК 5.1. Собирать исходные данные для разработки проектной документации на информационную систему.
ПК 9.2. Разрабатывать веб-приложение в соответствии с техническим заданием. ПК 10.1. Обрабатывать статический и динамический информационный контент.
ПК 11.1. Осуществлять сбор, обработку и анализ информации для проектирования баз данных.
1.2. Место дисциплины в структуре основной профессиональной образовательной программы: учебная дисциплина «Численные методы» принадлежит к общепрофессиональному циклу.
1.3. Цели и задачи учебной дисциплины – требования к результатам освоения дисциплины
Умения Знания
ОК 1, 2, 4, использовать основные численные методы хранения чисел в памяти
5, 9, 10, методы решения математических задач; электронно-вычислительной ПК 1.1, выбирать оптимальный численный машины (далее – ЭВМ) и
1.2, 1.5, метод для решения поставленной действия над ними, оценку
ПК 3.4, ПК задачи; точности вычислений;
давать математические характеристики
5.1, ПК методы решения основных
точности исходной информации и
9.2, ПК математических задач –
оценивать точность полученного
10.1, ПК интегрирования,
11.1. разрабатывать алгоритмы и программы дифференцирования, решения
линейных и трансцендентных для решения вычислительных задач,
уравнений и систем уравнений с учитывая необходимую точность
помощью ЭВМ. получаемого результата.
1.4. Рекомендуемое количество часов на освоение учебной дисциплины
В соответствии с ФГОС СПО по специальности 09.02.03 Программирование в компьютерных системах и по Учебному плану на освоение учебной дисциплины «Численные методы» отводится максимальной учебной нагрузки студента 56 часа, в том числе:
обязательной аудиторной учебной нагрузки – 54 часа, самостоятельной работы студента – 2 часов.
Практические занятия 14 часов
2. СТРУКТУРА И ПРИМЕРНОЕ СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ «ОП.10. ЧИСЛЕННЫЕ МЕТОДЫ»
2.1. Объем учебной дисциплины и виды учебной работы
Объем в Коды компетенций, Наименование Содержание учебного материала и формы организации часах формированию
разделов и тем деятельности обучающихся которых способствует
элемент программы 1 2 3 4
Тема 1. Элементы Содержание учебного материала 4 ОК 1, 2, 4, 5, 9, 10,
теории Источники и классификация погрешностей результата численного ПК 1.1, 1.2, 1.5, ПК 3.4, погрешностей решения задачи. ПК 5.1, ПК 9.2, ПК
В том числе практических занятий и лабораторных работ 10.1, ПК 11.1.
Самостоятельная работа обучающихся
Тема 2. Содержание учебного материала 6 ОК 1, 2, 4, 5, 9, 10,
Приближённые Постановка задачи локализации корней. Численные методы ПК 1.1, 1.2, 1.5, ПК 3.4, решения решения уравнений. ПК 5.1, ПК 9.2, ПК алгебраических и В том числе практических занятий и лабораторных работ 10.1, ПК 11.1.
трансцендентных Самостоятельная работа обучающихся уравнений
Тема 3. Решение Содержание учебного материала 6 ОК 1, 2, 4, 5, 9, 10,
систем линейных Метод Гаусса. Метод итераций решения СЛАУ. Метод Зейделя. ПК 1.1, 1.2, 1.5, ПК 3.4, алгебраических В том числе практических занятий и лабораторных работ ПК 5.1, ПК 9.2, ПК уравнений Самостоятельная работа обучающихся 10.1, ПК 11.1. Тема 4. Содержание учебного материала 6 ОК 1, 2, 4, 5, 9, 10,
Интерполирование Интерполяционный многочлен Лагранжа. Интерполяционные ПК 1.1, 1.2, 1.5, ПК 3.4, и формулы Ньютона. ПК 5.1, ПК 9.2, ПК экстраполирование Интерполирование сплайнами. 10.1, ПК 11.1.
функций В том числе практических занятий и лабораторных работ
Тема 5. Численное Содержание учебного материала 8 ОК 1, 2, 4, 5, 9, 10,
интегрирование Формулы Ньютона — Котеса: методы прямоугольников, трапеций, ПК 1.1, 1.2, 1.5, ПК 3.4, парабол. ПК 5.1, ПК 9.2, ПК
Интегрирование с помощью формул Гаусса. 10.1, ПК 11.1.
В том числе практических занятий и лабораторных работ
Самостоятельная работа обучающихся
Тема 6. Численное Содержание учебного материала 8 ОК 1, 2, 4, 5, 9, 10,
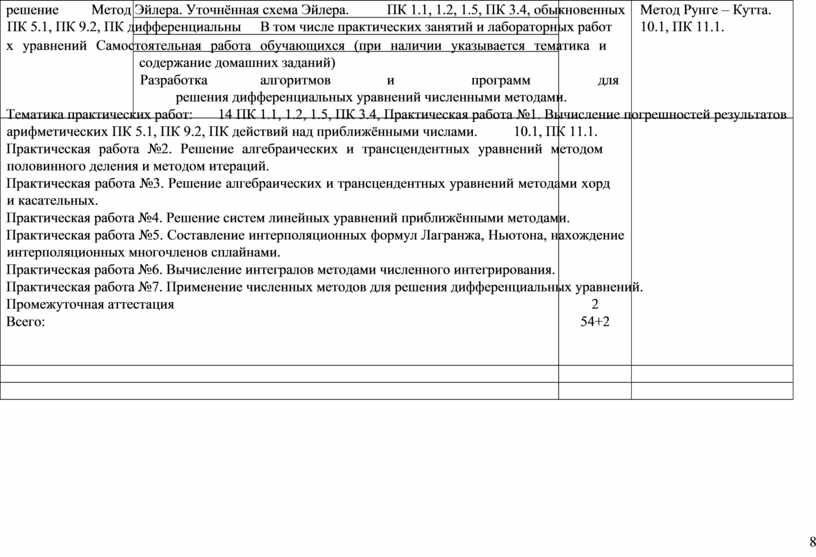
решение Метод Эйлера. Уточнённая схема Эйлера. ПК 1.1, 1.2, 1.5, ПК 3.4, обыкновенных Метод Рунге – Кутта. ПК 5.1, ПК 9.2, ПК дифференциальны В том числе практических занятий и лабораторных работ 10.1, ПК 11.1.
Разработка алгоритмов и программ для решения дифференциальных уравнений численными методами.
Тематика практических работ: 14 ПК 1.1, 1.2, 1.5, ПК 3.4, Практическая работа №1. Вычисление погрешностей результатов арифметических ПК 5.1, ПК 9.2, ПК действий над приближёнными числами. 10.1, ПК 11.1.
Практическая работа №2. Решение алгебраических и трансцендентных уравнений методом половинного деления и методом итераций.
Практическая работа №3. Решение алгебраических и трансцендентных уравнений методами хорд и касательных.
Практическая работа №4. Решение систем линейных уравнений приближёнными методами.
Практическая работа №5. Составление интерполяционных формул Лагранжа, Ньютона, нахождение интерполяционных многочленов сплайнами.
Практическая работа №6. Вычисление интегралов методами численного интегрирования.
Практическая работа №7. Применение численных методов для решения дифференциальных уравнений.
Промежуточная аттестация 2
3. УСЛОВИЯ РЕАЛИЗАЦИИ ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ «ОП.10. ЧИСЛЕННЫЕ МЕТОДЫ»
3.1. Для реализации программы учебной дисциплины должны быть предусмотрены следующие специальные помещения:
Кабинет «Математические дисциплины», оснащенный оборудованием и техническими средствами обучения:
— рабочее место преподавателя;
— посадочные места обучающихся (по количеству обучающихся);
— учебные наглядные пособия (таблицы, плакаты);
— тематические папки дидактических материалов;
— комплект учебно-методической документации;
— комплект учебников (учебных пособий) по количеству обучающихся.
Технические средства обучения:
— компьютер с лицензионным программным обеспечением;
3.2. Информационное обеспечение реализации программы
Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы
3.2.1. Печатные издания
1.Численные методы и программирование: Учебное пособие / В.Д. Колдаев; Под ред. Л.Г. Гагариной. — М.: ИД ФОРУМ: НИЦ Инфра-М, 2013. — 336 с.
2. Бартеньев О.В. Фортран для студентов. М.: Диалог–МИФИ, 2006. 397 с.
3. Бахвалов Н.С. Численные методы. М.: Наука, 2006. 631 с.
4. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. 3-е изд., перераб. идоп. М.: БИНОМ. Лаборатория знаний, 2009. 632 с.
5. Воробьев Г. Н., Данилова А. Н. “Практикум по численным методам.” — М.:”Высш.шк.”, 2007 г. -184 с.
6. Данко П.Е. Высшая математика в упражнениях и задачах: В 2т. учеб. пособ. – М.: Высш. шк., 2008. 3. Исаков В.Н. Элементы численных методов: учеб. пособ. – М.: Академия, 2008.
7. Протасов И.Д. Лекции по вычислительной математике: учеб. пособ. – М.: ГелиосАРВ, 2009.
3.2.2. Электронные издания (электронные ресурсы)
1. EqWorld. МИР МАТЕМАТИЧЕСКИХ УРАВНЕНИЙ http://eqworld.ipmnet.ru/ru/library.htm 2. Сайт журнала «Математика. Приложение к газете «Первое сентября»» http://mat.1september.ru/
3. Математический портал http://www.allmath.ru/
4. Exponenta – образовательный математический сайт https://exponenta.ru/
5. Информационная система Math-Net.Ru http://www.mathnet.ru/
6. ALGLIB — кросс-платформенная библиотека численного анализа http://alglib.sources.ru/
3.2.3. Дополнительные источники
1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.П. Численные методы. М.; СПб.: Лаборатория базовых знаний, 2012
2. Костомаров Р.П., Корухова Л.С., Манжелей С.Г. Программирование и численныеметоды. М.: Издательство МГУ, 2013
3. Воробьева Г.Н., Данилова А.Н. Практикум по вычислительной математике. М.: Высшая школа, 2013
4. Куприянова Л.М. Программирование, алгебраические языки и вычислительнаяматематика. М.: Финансы и статистика, 2013.
5. Костомаров, Д.П. Вводные лекции по численным методам: Учеб. пособие / Д.П.
Костомаров, А.П. Фаворский. – М.: Логос, 2004. – 184 с.
6. Турчак, Л. И. Основы численных методов. 2-е изд, перераб. и доп. М., 2003. 3. Лапчик, М. П. Численные методы. 2-e изд., стер.
М., 2005.
7. Калиткин, Н.Н. Численные методы. – М.: Наука, 1978. 5. Бахвалов, Н.С. Численныеметоды. – М.: Наука, 1975.
8. Бахвалов, Н.С. Численные методы / Н.С. Бахвалов, Н.П. Жидков, Г.М. Ко- бельков. –М.: Наука, 1987. 7. Ортега, Дж. Введение в параллельные и векторные методы решения линей- ных систем / Дж.
Ортега. – М.: Мир, 1991.
9. Писсанецки, С. Технология разреженных матриц / С. Писсанецки. – М.: Мир, 1988.
10. Фаддеев, Л.К. Вычислительные методы линейной алгебры / Л.К. Фаддеев, В.Н.
Фаддеева. – М.: Физматгиз, 1963.
11. Воеводин, В.В. Вычислительные основы линейной алгебры / В.В. Воеводин. – М.: Наука, 1977.
12. Ортега, Дж. Введение в численные методы решения дифференциальныхуравнений / Дж. Ортега. – М.: Наука, 1986.
13. Райс, Дж. Матричные вычисления и математическое обеспечение / Дж. Райс. – М.:
4. КОНТРОЛЬ И ОЦЕНКА РЕЗУЛЬТАТОВ ОСВОЕНИЯ УЧЕБНОЙ ДИСЦИПЛИНЫ «ОП.10. ЧИСЛЕННЫЕ МЕТОДЫ»
Образовательное учреждение, реализующее подготовку по учебной дисциплине, обеспечивает организацию и проведение завершающей аттестации и текущего контроля демонстрируемых обучающимися знаний, умений и навыков. Текущий контроль проводится преподавателем в процессе проведения практических занятий, тестирования, а также выполнения обучающимися индивидуальных заданий. Формы и методы текущего контроля по учебной дисциплине самостоятельно разрабатываются образовательным учреждением и доводятся до сведения обучающихся в начале обучения.
Для текущего контроля образовательными учреждениями создаются фонды оценочных средств (ФОС).
ФОС включают в себя педагогические контрольно-измерительные материалы, предназначенные для определения соответствия (или несоответствия) индивидуальных образовательных достижений основным показателям результатов подготовки (таблица).
Формы и методы
Результаты обучения Критерии оценки
методы решения основных полностью, без пробелов, некоторые работа математических задач – умения сформированы недостаточно, •
интегрирования, все предусмотренные программой
Самостоятельная дифференцирования, учебные задания выполнены, работа решения линейных и некоторые виды заданий выполнены
• Защита трансцендентных с ошибками.
реферата уравнений и систем «Удовлетворительно» —
ЭВМ. освоено частично, но пробелы не • Защита
Перечень умений, носят существенного характера, курсовой работы осваиваемых в рамках необходимые умения работы с (проекта) дисциплины: освоенным материалом в основном • Выполнение использовать основные сформированы, большинство проекта численные методы предусмотренных программой • Наблюдение за решения математических обучения учебных заданий выполнением
задач; выполнено, некоторые из практического выбирать оптимальный выполненных заданий содержат задания.
численный метод для ошибки. (деятельностью
давать математические освоено, необходимые умения не выполнения характеристики точности сформированы, выполненные практического исходной информации и учебные задания содержат грубые задания(работы)
оценивать точность ошибки. • Подготовка и полученного численного выступление с
разрабатывать алгоритмы сообщением, и программы для решения презентацией вычислительных задач, • Решение
учитывая необходимую ситуационной задачи точность получаемого результата.
Качественная оценка индивидуальных
Процент образовательных достижений
результативности
(правильных ответов) балл вербальный
(отметка) аналог
90 ÷ 100 5 отлично
80 ÷ 89 4 хорошо
70 ÷ 79 3 удовлетворительно
Министерство общего и профессионального образования

Рабочая программа учебной дисциплины разработана на основе

Разработчик: Кондрашова Юлия


ПК 9.2. Разрабатывать веб-приложение в соответствии с техническим заданием

Практические занятия 14 часов 2
Метод Эйлера. Уточнённая схема
УСЛОВИЯ РЕАЛИЗАЦИИ

EqWorld. МИР МАТЕМАТИЧЕСКИХ УРАВНЕНИЙ http://eqworld

КОНТРОЛЬ И ОЦЕНКА РЕЗУЛЬТАТОВ

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
Источник: znanio.ru
Численные методы. ОП.10 Численные методы. Рабочая программа учебной дисциплины оп. 10 Численные методы 2021 г

Единственный в мире Музей Смайликов
Самая яркая достопримечательность Крыма

Скачать 432.89 Kb.
ПРИЛОЖЕНИЕ
РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
ОП.10 ЧИСЛЕННЫЕ МЕТОДЫ
2021 г.
2
Рабочая программа учебной дисциплины разработана на основе Федерального государственного образовательного стандарта среднего профессионального образования (далее
– ФГОС СПО) по специальности 09.02.07 «Информационные системы и программирование», примерной основной образовательной программы по специальности
09.02.07
«Информационные системы и программирование», профессионального стандарта 06.015
«Специалист по информационным системам» (утвержден приказом Министерства труда и социальной защиты Российской Федерации от 18 ноября 2014 г. N 896н).
Организация-разработчик:
Государственное автономное профессиональное образовательное учреждение
Свердловской области
«Екатеринбургский экономико-технологический колледж», г. Екатеринбург
Разработчик:
Молокитина Дарья Дмитриевна — преподаватель
Рассмотрена на заседании предметной
(цикловой) комиссии математических и естественнонаучных дисциплин
Председатель П(Ц)К
___________________ И.Д. Фельдман
Протокол № 10 от «29» июня 2021г.
Рассмотрена на заседании методического совета ГАПОУ СО «Екатеринбургский экономико-технологический колледж»
Протокол № 5 от «30» июня 2021г.
Утверждаю:
заместитель директора по учебной работе
________________ Е. А. Баранцева
«30» июня 2021г.
3
СОДЕРЖАНИЕ
1. ОБЩАЯ ХАРАКТЕРИСТИКА РАБОЧЕЙ ПРОГРАММЫ УЧЕБНОЙ
ДИСЦИПЛИНЫ
4 2. СТРУКТУРА И СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ
6 3. УСЛОВИЯ РЕАЛИЗАЦИИ ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ
12 4. КОНТРОЛЬ И ОЦЕНКА РЕЗУЛЬТАТОВ ОСВОЕНИЯ УЧЕБНОЙ
ДИСЦИПЛИНЫ
13
4
1. ОБЩАЯ ХАРАКТЕРИСТИКА РАБОЧЕЙ ПРОГРАММЫ УЧЕБНОЙ
ДИСЦИПЛИНЫ ОП.10 ЧИСЛЕННЫЕ МЕТОДЫ
Рабочая программа учебной дисциплины разработана на основе Федерального государственного образовательного стандарта среднего профессионального образования (далее
– ФГОС СПО) по специальности 09.02.07 «Информационные системы и программирование», квалификации
«Специалист по информационным системам», учетом требований профессионального стандарта 06.015 «Специалист по информационным системам» (утвержден приказом Министерства труда и социальной защиты Российской Федерации от 18 ноября 2014 г. N 896н).
1.1. Область применения рабочей программы
Рабочая программа учебной дисциплины ОП.10 Численные методы является частью основной образовательной программы в соответствии с ФГОС СПО по специальности 09.02.07
«Информационные системы и программирование»,квалификации «Специалист по информационным системам».
Рабочая программа учебной дисциплины может быть использована в дополнительном профессиональном образовании (в программах повышения квалификации и переподготовки) и профессиональной подготовке.
1.2. Место учебной дисциплины в структуре основной профессиональной
образовательной программы: учебная дисциплина ОП.10 Численные методы — дисциплина общепрофессионального цикла.
1.3. Цели и задачи учебной дисциплины – требования к результатам освоения
дисциплины
В результате освоения учебной дисциплины обучающимися осваиваются знания и умения, формируются общие компетенции:
Код ПК, ОК
Умения
Знания
ОК 01
ОК 02
ОК 04
ОК 05
ОК 09
ОК 10
ПК 3.4
ПК 5.1
использовать основные численные методы решения математических задач;
выбирать оптимальный численный метод для решения поставленной задачи;
давать математические характеристики точности
методы хранения чисел в памяти электронно-вычислительной машины (далее – ЭВМ) и действия над ними, оценку точности вычислений;
методы решения основных математических задач – интегрирования,
5 исходной информации и оценивать точность полученного численного решения;
разрабатывать алгоритмы и программы для решения вычислительных задач, учитывая необходимую точность получаемого результата. дифференцирования, решения линейных и трансцендентных уравнений и систем уравнений с помощью ЭВМ
1.4. Количество часов на освоение программы дисциплины
Объем образовательной нагрузки обучающегося 64 часа, в том числе: очная форма обучения заочная форма обучения аудиторной нагрузки обучающихся (теоретических занятий, практических работ)
56 самостоятельной работы обучающихся
4 консультаций
2
Консультаций перед экзаменом
—
Промежуточная аттестация (дифференцированный зачет)
2
6
2. СТРУКТУРА И СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ
2.1. Объем учебной дисциплины и виды учебной работы
Вид учебной работы
Объем часов
Объем образовательной нагрузки (всего)
64
Из них в форме практической подготовки
20
Всего по УД
56 в том числе: теоретических занятий
24 лабораторные занятия
— практические занятия
32 контрольные работы
— курсовая работа (проект)
—
Самостоятельная работа обучающегося (всего)
4 в том числе: составление таблиц
—
Решение ситуационных задач
4 работа с источниками
—
Консультации
2
Промежуточная аттестация в форме дифференцированного зачета
2
8
Практические занятия
ОК 9
ОК 10
ПК 3.4
ПК 5.1 1
Практическая работа №3. Примеры задач, приводящих к уравнениям /
Алгебраические и трансцендентные уравнения.
Задание на дом: № 8.8, 8.9, стр. 261, [1].
2
—
2
Практическая работа №4. Решение алгебраических и трансцендентных
уравнений / Метод половинного деления и метод итераций.
Задание на дом: № 8.20, 8.21, стр. 262, [1].
2
—
3
Практическая работа №5 Решение алгебраических и трансцендентных
уравнений / Метод хорд и касательных
Задание на дом: № 8.30, 8.31, стр. 263, [1]
2 2
Контрольные работы
1
Тема: решение алгебраических и трансцендентных уравнений методом итераций
2
—
Самостоятельная работа обучающихся
1
Подготовка конспекта по темам: Итерационный метод решения систем линейных алгебраических уравнений. Нахождение собственных значений матрицы.
2
—
Тема 3.
Решение
систем
линейных
алгебраических
уравнений
Содержание учебного материала
ОК 1
ОК 2
ОК 4
ОК 5
ОК 9
ОК 10
ПК 3.4
ПК 5.1 1
Метод Гаусса. Метод итераций решения СЛАУ / Метод Зейделя.
Задание на дом: № 10.7, стр. 266, № 10.17, стр. 278, [1].
2
—
Лабораторные работы
—
—
Практические занятия
1
Практическая работа № 6. Решение систем линейных уравнений / Метод
Жордана – Гаусса.
Задание на дом: № 10.9, 10.10, стр. 266, [1].
2
—
2
Практическая работа № 7. Вычисление обратной матрицы / Метод
Жордана – Гаусса.
Задание на дом: № 10.12, 10.13, стр. 267, [1].
2 2
9 3
Практическая работа № 8. Решение систем линейных уравнений /
Приближенные методы. Метод итераций. Инструментальные средства: табличный процессор Excel, система MathCad, система Matlab.
Задание на дом: № 10.16.1, 10.16.2, стр. 267, [1]
2 2
Контрольные работы
—
—
Самостоятельная работа обучающихся
—
—
Тема 4.
Интерполирование и
экстраполирование
функций
Содержание учебного материала
ОК 1
ОК 2
ОК 4
ОК 5
ОК 9
ОК 10
ПК 3.4
ПК 5.1 1
Интерполяционный многочлен Лагранжа / Интерполяционные формулы
Ньютона.
Задание на дом: выучить конспект
2
—
2
Интерполирование сплайнами / Оценка погрешности при интерполировании. Численное дифференцирование. Интерполирование с кратными узлами. Формула Эрмита
Задание на дом: № 15.2.3, 15.2.4, стр. 276, [1].
2 2
Лабораторные работы
—
—
Практические занятия
1
Практическая работа № 9. Постановка задачи интерполяции /
Интерполирование при помощи многочлена. Составление интерполяционных формул Лагранжа, Ньютона.
Задание на дом: № 15.2.5, 15.2.6, стр. 276, [1].
2
—
2
Практическая работа № 10.Нахождение интерполяционных многочленов
сплайнами.
Задание на дом: № 16.1, стр. 277, [1].
2
—
3
Практическая работа № 11. Оценка погрешности при интерполировании/
Конечные разности. Разделенные разности.
Задание на дом: оформить отчет по практической работе
2
—
4
Практическая работа № 12. Аппроксимация методом наименьших
квадратов.
Задание на дом: № 16.2, стр. 277, [1].
2
—
Контрольные работы
—
—
10
Самостоятельная работа обучающихся
—
—
Тема 5.
Численное
интегрирование
Содержание учебного материала
ОК 1
ОК 2
ОК 4
ОК 5
ОК 9
ОК 10
ПК 3.4
ПК 5.1 1
Постановка задачи о численном интегрировании / Основные формулы численного интегрирования.
Задание на дом: № 12.1.3, 12.1.4, стр. 269, [1].
2 2
2
Формулы Ньютона – Котеса / Методы прямоугольников, трапеций, парабол.
Задание на дом: № 12.1.5, 12.1.6, стр. 270, [1].
2
—
3
Интегрирование с помощью формул Гаусса, формулы Симпсона
(парабол).
Задание на дом: № 12.2.3, 12.2.4, стр. 271, [1].
2 2
Лабораторные работы
—
—
Практические занятия
1
Практическая работа № 13. Вычисление интегралов методами
прямоугольников, трапеций.
Задание на дом: № 12.1.7, 12.1.8, стр. 270, [1].
2
—
2
Практическая работа № 14. Правило Рунге оценки погрешностей
вычисления интегралов.
Задание на дом: № 12.2.5, 12.2.6, стр. 271, [1].
2
—
Контрольные работы
1
Тема: Численное интегрирование методом трапеций и с помощью формулы
Симпсона.
2
—
Самостоятельная работа обучающихся
—
—
Тема 6.
Численное решение
обыкновенных
дифференциальных
уравнений
Содержание учебного материала
ОК 1
ОК 2
ОК 4
ОК 5 1
Задача численного интегрирования дифференциальных уравнений.
Задание на дом: № 14.1.5, 14.1.6, стр. 274, [1].
2 2
2
Простейшие методы численного интегрирования дифференциальных
уравнений / Метод Эйлера. Уточнѐнная схема Эйлера. Метод Рунге – Кутта.
Задание на дом: № 14.1.9, 14.1.10, стр. 274, [1].
2
—
11
Лабораторные работы
—
—
ОК 9
ОК 10
ПК 3.4
ПК 5.1
Практические занятия
1
Практическая работа № 15. Применение численных методов для
решения дифференциальных уравнений / Метод Эйлера. Уточнѐнная схема Эйлера.
Задание на дом: № 14.2.6, 14.2.7, стр. 274, [1].
2 2
2
Практическая работа № 16. Метод Рунге – Кутта решения
дифференциальных уравнений.
Задание на дом: № 14.2.21, 14.2.22, стр. 275, [1].
2
—
Контрольные работы
—
—
Самостоятельная работа обучающихся
1
Вычисление интегралов с помощью формул Гаусса и Симпсона
2
—
Консультация
2
—
Дифференцированный зачет
2
—
Всего
64 20
12
3. УСЛОВИЯ РЕАЛИЗАЦИИ ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ
3.1. Для реализации программы учебной дисциплины в колледже предусмотрены
следующие специальные помещения: кабинет «Математики и статистики», оснащенный оборудованием: доской учебной, рабочим местом преподавателя, столами, стульями (по числу обучающихся), техническими средствами обучения (компьютером, наглядными пособиями); и лаборатория «Программного обеспечения и сопровождения компьютерных систем».
Оборудование учебного кабинета: автоматизированные рабочие места на 12-15 обучающихся
(процессор Intel Core i5- 4460, оперативная память объемом 8 Гб); автоматизированное рабочее место преподавателя (процессор Intel Core i5-4460, оперативная память объемом 8 Гб);
проектор и экран; маркерная доска. Программное обеспечение общего и профессионального назначения, в том числе включающее в себя ПО MS Office.
3.2. Информационное обеспечение реализации программы
Перечень рекомендуемых учебных изданий, дополнительной литературы, Интернет- ресурсов:
3.2.1. Печатные издания
1. Колдаев В.Д. Численные методы и программирование: учеб. пособие / В.Д. Колдаев; под ред. проф. Л.Г. Гагариной. – М.: ИД «ФОРУМ»: ИНФРА-М, 2020. – 336 с – (Среднее профессиональное образование).
3.2.2. Электронные ресурсы:
http://www.knigafund.ru/books/185553 — сайт Издательства Юрайт Соболева О.Н.
Введение в численные методы: учебное пособие http://wiki.cs.hse.ru/Численные_методы — сайт НИУ ВШЭ факультета компьютерных наук
Дополнительные источники
1. Гателюк О.В. Численные методы: учеб. пособие для СПО / О.В. Гателюк, Ш.К.
Исмаилов, Н.В. Манюкова. – М.: Издательство Юрайт, 2018. – 140 с.
2. Лапчик М.П. Численные методы: учебник для студентов средних профессиональных учебных заведений / М.П. Лапчик, М.И. Рагулина, Е.К. Хеннер; Под ред.
М.П. Лапчика. – 5-е изд. – М.: Издательский центр «Академия», 2018. – 251 с.
3. Пирумов У.Г. Численные методы: учебник и практикум для академического бакалавриата/ У.Г. Пирумов: под ред. У.Г. Пирумова. – 5-е изд., перераб. и доп. – М.:
Издательство Юрайт, 2018. – 421 с.
13
4. КОНТРОЛЬ И ОЦЕНКА РЕЗУЛЬТАТОВ ОСВОЕНИЯ УЧЕБНОЙ ДИСЦИПЛИНЫ
Контроль и оценка результатов освоения дисциплины осуществляется преподавателем в процессе проведения практических занятий и лабораторных работ, тестирования, а также выполнения обучающимися индивидуальных заданий, проектов, исследований.
Результаты обучения
(знания, умения, коды формируемых ОК, ПК)
Формы и методы контроля
и оценки результатов обучения
Перечень умений, осваиваемых в рамках дисциплины:
использовать основные численные методы решения математических задач;
выбирать оптимальный численный метод для решения поставленной задачи;
давать математические характеристики точности исходной информации и оценивать точность полученного численного решения;
разрабатывать алгоритмы и программы для решения вычислительных задач, учитывая необходимую точность получаемого результата;
ОК 1, ОК 2, ОК 4, ОК 5, ОК 9, ОК 10,
ПК 3.4, ПК 5.1
Компьютерное тестирование на знание терминологий по темам:
Элементы теории погрешностей;
Решение систем линейных алгебраических уравнений.
Контрольные работы по темам:
«Решение алгебраических и трансцендентных уравнений методом итераций», «Численное интегрирование методом трапеций и с помощью формулы Симпсона».
Самостоятельная работа: а)
Подготовка конспекта по темам:
Итерационный метод решения систем линейных алгебраических уравнений.
Нахождение собственных значений матрицы; б) Вычисление интегралов с помощью формул Гаусса и Симпсона
Наблюдение за выполнением практического задания (в MS Office
Excel.
Оценка выполнения практического задания
(работы)
Решение ситуационных задач по использованию численных методов решения уравнений.
Перечень знаний, осваиваемых в рамках дисциплины:
методы хранения чисел в памяти электронно- вычислительной машины (далее – ЭВМ) и действия над ними, оценку точности вычислений;
методы решения основных математических задач интегрирования, дифференцирования, решения линейных и трансцендентных уравнений и систем уравнений с помощью ЭВМ;
ОК 1, ОК 2, ОК 4, ОК 5, ОК 9, ОК 10,
ПК 3.4, ПК 5.1
Источник: topuch.com