Октава программа как работать

GNU Octave — это использующая совместимый с MATLAB язык высокого уровня свободная программная система, предназначенная для математических вычислений.

Общие сведения о программной системе GNU Octave

Расчетные операции могут иметь разную сложность, например, определить результат произведения шесть на, подсчитать общую сумму стоимости товаров в чеке, найти решение системы линейных уравнений для домашнего задания ученика или, к примеру, выполнить расчет деградации волнового фронта при прохождении многослойной турбулентной атмосферы.

Если расчет первых двух примеров можно осуществить на обычном калькуляторе, то линейные уравнения уже можно решить только на специальном инженерном калькуляторе. А последний пример может быть решен только при помощи системы численных расчетов, используемой для научных исследований, такой как, к примеру, GNU Octave.

GNU Octave является открытым программным обеспечением для математических расчетов, которое известно тем, что способно поддерживать совместимость с коммерческим MATLAB на достаточно высоком уровне. То есть, практически это программное обеспечение является клоном MATLAB, так как даже незначительная несовместимость может рассматриваться проектировщиками как ошибка.

Octave. Установка пакетов

Изначально Octave разрабатывался как сопутствующее программное обеспечение для учебного курса для студентов, изучающих проектирование химических реакторов. Позднее главный специалист J.W. Eaton модифицировал полностью законченный продукт и теперь он стал активно использоваться как для производственных целей, так и для академических. Наиболее часто Octave применяют для матричных вычислений и это обладает определенным смыслом, поскольку большинство инженерных проблем и отображение данных наиболее часто предполагают векторный и матричный подход.

Математические вычисления в GNU Octave

Существует довольно много языков программирования, например, Cи, Python, Java, позволяющих решать описанные выше задачи, но, когда работа доходит до этапа формирования концепции, главным аспектом становится оперативность реализации, то есть период времени, который необходим для того, чтобы реализовать алгоритм. И MATLAB, и Octave как раз были спроектированы для решения задач подобного типа, осуществления вычислений и выдачи итоговых результатов на экран монитора.

«Математические вычисления в GNU Octave»
Готовые курсовые работы и рефераты
Решение учебных вопросов в 2 клика
Помощь в написании учебной работы

Octave имеет обширный инструментальный набор, предназначенный для решения общих задач численной линейной алгебры, определения корней нелинейных уравнений, интегрирования обычных функций, манипулирования полиномами и интегрирования обыкновенных дифференциальных и дифференциально-алгебраических уравнений. Octave может быть легко расширен пользовательскими функциями, которые могут быть написаны на собственном языке данной программы или, при помощи динамически загружаемых модулей, сформированные на C/C++, Fortran и иных языках.

Знакомство с MATLAB (GNU Octave) (лаб. работа)

Возможны следующие варианты применения данного языка программирования:

1. Изучение и проектирование концептов на производстве, а также и в академических направлениях.
2. Возможность получить аналогичный по функциональному набору MATLAB программный продукт, но который является бесплатным.
3. Возможность разработки и тестирования математических алгоритмов.

В качестве практического использования программы Octave можно привести следующие реальные примеры:

1. NASA применяет Octave при проектировании систем стыковки космических аппаратов.
2. Jaguar использует Octave для анализа данных, получаемых от их болидов Formula 1.
3. Шеффилдский Университет применяет Octave при проектировании программного обеспечения, предназначенного для распознавания раковых клеток.

Как следует из приведенных выше примеров, сфер применения этой программы может быть очень много, и она естественно предоставляет возможность написания программ в оперативном режиме, а также возможность визуализации данных во многих сферах и направлениях.

Программа Octave способна поддерживать следующий набор арифметических операций:

1. Операцию сложения (+).
2. Операцию вычитания (-).
3. Операцию умножения (*).
4. Операцию деления (/).
5. Операцию возведение в степень (^).
6. Операции с натуральными логарифмами/показателями (log, exp),
7. Операции с тригонометрическими функциями (sin, cos, м другими).

Помимо этого, Octave способна работать как с вещественными числами, так и с комплексными (i, j). Также являются предопределенными определенные математические константы, к примеру, число π (pi) и основание натурального логарифма e.

Векторы и матрицы являются базовыми строительными блоками численного анализа. Для того чтобы создать матрицу и сохранить ее в переменной для дальнейшего применения следует использовать следующую команду:

$>>$ A = [ 1, 1, 2; 3, 5, 8; 13, 21, 34 ]

В результате будет выдан такой ответ:

Если выполнить ввод команды, установив в конце символ точка с запятой, то Octave не станет осуществлять вывод матрицы на экран. К примеру, можно создать матрицу на три строки и два столбца, заполненную случайными числами:

А далее для того, чтобы вывести данную матрицу на дисплей, следует просто задать в командном окне имя переменной, в которой она была сохранена:

Приведем примеры выполнения некоторых арифметических операций. Рассмотрим умножение матрицы на скалярную величину:

Далее рассмотрим перемножение двух матриц:

Пример умножения транспонированной матрицы на саму себя:

Далее рассмотрим решение системы линейных уравнений на примере следующего уравнения:

$X_1 + 3X_2 + 5X_3 = 22$

$3X_1 + X_2 + 3X_3 = 14$

$4X_1 + X_2 + 3X_3 = 15$

Сформируем матрицы коэффициентов и свободных членов для данной системы уравнений:

Рисунок 1. Матрицы. Автор24 — интернет-биржа студенческих работ

А затем наберем обе эти сформированные матрицы в Octave и решим систему методом наименьших квадратов при помощи специального оператора левого деления :

$>>$ A = [1 3 5; 3 1 3; 4 1 3];

Последние три цифры выше являются ответом, то есть, решением.

Источник: spravochnick.ru

Введение в Octave для инженеров и математиков, Алексеев Е.Р., Чеснокова О.В., 2012

Введение в Octave для инженеров и математиков, Алексеев Е.Р., Чеснокова О.В., 2012.

Книга посвящена свободно распространяемому пакету Octave. Читатель держит в руках первое описание пакета на русском языке. Описан встроенный язык пакета, подробно рассмотрены графические возможности пакета. Подробно рассмотрено решение различных инженерных и математических задач.

Особое внимание уделено операциям с матрицами, решению нелинейных уравнений и систем, дифференцированию и интегрированию, решению дифференциальных уравнений, оптимизационным задачам и обработке экспериментальных данных (интерполяции и аппроксимации). Наряду со встроенным языком пакета описана среда QtOctave.

Введение.

Книга, которую держит в руках читатель, посвящена GNU Octave — одной из самых интересных прикладных программ для решения инженерных и математических задач. GNU Octave — это свободный интерпретирующий язык для проведения математических вычислений.

По возможностям и качеству реализации интерпретатора язык Octave можно сравнивать с проприетарной программой MATLAB, причём синтаксис обоих языков очень схож. Существуют версии языка для различных дистрибутивов GNU Linux (ALT Linux, Debian, Ubuntu, Mandriva и др.) и для ОС Windows. На наш взгляд, GNU Octave больше ориентирован на работу в Linux. Работа в ОС Windows возможна, но пользователю Windows надо быть готовым работать с простым текстовым редактором и командной строкой.

Оглавление.

Введение
Глава 1. Общие сведения, установка
Глава 2. Основы работы
Глава 3. Программирование
Глава 4. Построение графиков
Глава 5. Задачи линейной алгебры
Глава 6. Векторная алгебра и аналитическая геометрия
Глава 7. Нелинейные уравнения и системы
Глава 8. Интегрирование и дифференцирование
Глава 9. Решение обыкновенных дифференциальных уравнений
Глава 10. Решение оптимизационных задач
Глава 11. Метод наименьших квадратов
Глава 12. Интерполяция функций
Список литературы
Предметный указатель

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Введение в Octave для инженеров и математиков, Алексеев Е.Р., Чеснокова О.В., 2012 — fileskachat.com, быстрое и бесплатное скачивание.

Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России. Купить эту книгу

Источник: obuchalka.org

Общие сведения, установка

Курс посвящен GNU Octave — одной из самых интересных прикладных программ для решения инженерных и математических задач.

GNU Octave — это свободный интерпретирующий язык для проведения математических вычислений. По возможностям и качеству реализации интерпретатора язык Octave можно сравнивать с проприетарной программой MATLAB, причём синтаксис обоих языков очень схож.

Существуют версии языка для различных дистрибутивов GNU Linux ( ALT Linux, Debian, Ubuntu, Mandriva и др.) и для ОС Windows . На наш взгляд, GNU Octave больше ориентирован на работу в Linux. Работа в ОС Windows возможна, но пользователю Windows надо быть готовым работать с простым текстовым редактором и командной строкой.

Когда авторы начинали знакомиться с GNU Octave, основной проблемой было отсутствие хорошего русскоязычного введения в этот язык. Наша книга является попыткой восполнить этот пробел . Поэтому большое внимание было уделено самому языку (глава 3), операциям с матрицами (глава 5) и графическим возможностям пакета (глава 4).

Наш многолетний опыт преподавания информационных дисциплин в Донецком национальном техническом университете говорит нам о том, что студенту и инженеру наряду с описанием функций, предназначенных для решения той или иной задачи, не лишним будет напомнить и математическую постановку решаемой задачи, а зачастую и численные методы решения задачи. Именно поэтому в ряде глав приведены не только описания функций, но и описаны численные методы решения задач.

Что касается графических оболочек, таких как qtOctave, Xoctave и Kalculus , нами принято решение кратко описать наиболее стабильную из них, qtOctave , а основное внимание в книге уделить собственно языку. Мы считаем, что GNU Octave — это в первую очередь мощный интерпретирующий язык. Зная его, пользователь сможет работать с любой графической оболочкой.

Авторы выражают благодарность компании ALT Linux за многолетнее сотрудничество и возможность издать очередную книгу.

Донецк, апрель 2012

1.1 Принципы работы с интерпретатором

Octave — высокоуровневый интерпретируемый язык программирования , предназначенный для решения задач вычислительной математики. В состав пакета входит интерактивный командный интерфейс ( интерпретатор Octave). Интерпретатор Octave запускается из терминала ОС Linux или из его порта в Windows . После запуска Octave пользователь видит окно интерпретатора (рис. 1.1).

В окне интерпретатора пользователь может вводить как отдельные команды языка Octave, так и группы команд, объединяемые в программы. Если строка заканчивается символом «;», результаты на экран не выводятся. Если же в конце строки символ «;» отсутствует,

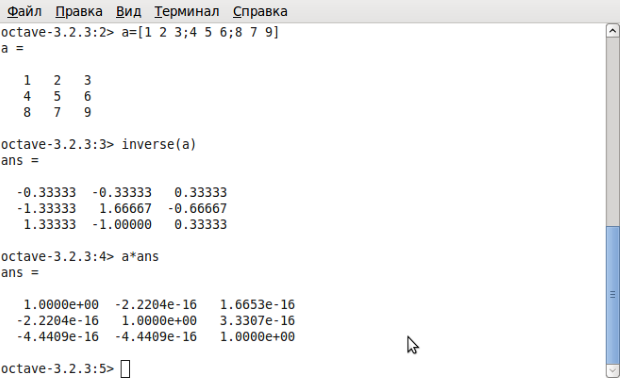
Рис. 1.1. Окно интерпретатора Octave

Рис. 1.2. Использование символов «;» и «%» в Octave

результаты работы выводятся на экран (рис. 1.2). Текст в строке после символа ( процент ) является комментарием и интерпретатором не обрабатывается (рис. 1.2). (Строки комментариев авторы книги будут использовать для пояснения функций и текстов программ.) Рассмотрим несколько несложных примеров.

Пример 1.1. Решить систему линейных алгебраических уравнений (СЛАУ)

Возможны два варианта решения любой задачи в Octave:

1. Терминальный режим. В этом режиме в окно интерпретатора последовательно вводятся отдельные команды.
2. Программный режим. В этом режиме создаётся текстовый файл с расширением .m , в котором хранятся последовательно выполняемые команды Octave. Затем этот текстовый файл (программа на языке Octave) запускается на выполнение в среде Octave.

Для решения СЛАУ в окне интерпретатора Octave последовательно введём следующие команды:

% Определение матрицы коэффициентов системы линейных уравнений. A=[3 5 -7; 3 -4 33; 22 -11 17]; b=[11; 25; 22]; % Вектор правых частей СЛАУ. x=A^(-1)*b % Решение системы методом обратной матрицы. x= 1.56361 2.55742 0.92542 octave -3.2.3:27 > A*x % Проверка. ans = 11.000 25.000 22.000
Листинг 1.1. Решение СЛАУ примера 1.1

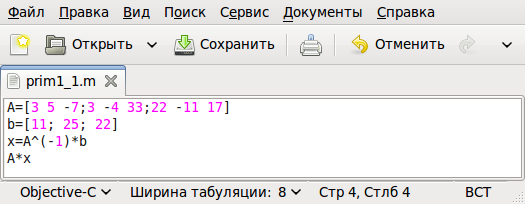
Рис. 1.3. Программа для решения примера 1.1

В переменной хранится результат последней операции , если команда не содержит знака присваивания. Следует помнить, что значение переменной изменяется после каждого вызова команды без операции присваивания.

Теперь рассмотрим, как решить эту же задачу в программном режиме. Вызовем любой текстовый редактор . (Именно текстовый редактор ! Не путайте с текстовыми процессорами типа Microsoft Word или OpenOffice.org/LibreOffice Writer.) Например gedit , в окне которого последовательно введём следующие команды:

A=[3 5 -7; 3 -4 33; 22 -11 17] b =[11; 25; 22] x=A^(-1)*b A*x

Сохраним введённые команды в виде файла с расширением .m , например, /home/evgeniy/prim1_1.m (рис. 1.3). Теперь эту программу необходимо запустить на выполнение из интерпретатора. Для этого в окне интерпретатора введём команды:

cd ’/home/evgeniy’% Переход в каталог, где хранится программа. prim1_1 % Запуск программы.

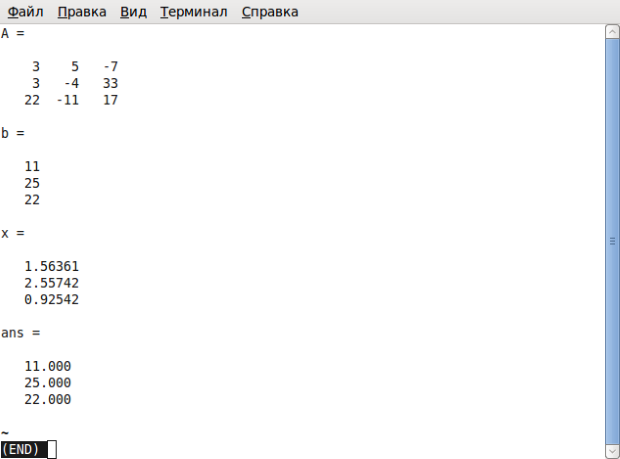
Рис. 1.4. Окно терминала после запуска программы prim1_1

Окно интерпретатора примет вид, представленный на рис. 1.4. Просмотрев результаты работы программы, нажмите для возвращения в режим ввода команд терминала.

Источник: intuit.ru