Octave программа что это

Математические вычисления в GNU Octave

GNU Octave — это использующая совместимый с MATLAB язык высокого уровня свободная программная система, предназначенная для математических вычислений.

Общие сведения о программной системе GNU Octave

Расчетные операции могут иметь разную сложность, например, определить результат произведения шесть на, подсчитать общую сумму стоимости товаров в чеке, найти решение системы линейных уравнений для домашнего задания ученика или, к примеру, выполнить расчет деградации волнового фронта при прохождении многослойной турбулентной атмосферы.

Если расчет первых двух примеров можно осуществить на обычном калькуляторе, то линейные уравнения уже можно решить только на специальном инженерном калькуляторе. А последний пример может быть решен только при помощи системы численных расчетов, используемой для научных исследований, такой как, к примеру, GNU Octave.

Решим твою учебную задачу всего за 30 минут
Попробовать прямо сейчас

GNU Octave является открытым программным обеспечением для математических расчетов, которое известно тем, что способно поддерживать совместимость с коммерческим MATLAB на достаточно высоком уровне. То есть, практически это программное обеспечение является клоном MATLAB, так как даже незначительная несовместимость может рассматриваться проектировщиками как ошибка.

Octave. Установка пакетов

Изначально Octave разрабатывался как сопутствующее программное обеспечение для учебного курса для студентов, изучающих проектирование химических реакторов. Позднее главный специалист J.W. Eaton модифицировал полностью законченный продукт и теперь он стал активно использоваться как для производственных целей, так и для академических. Наиболее часто Octave применяют для матричных вычислений и это обладает определенным смыслом, поскольку большинство инженерных проблем и отображение данных наиболее часто предполагают векторный и матричный подход.

Математические вычисления в GNU Octave

Существует довольно много языков программирования, например, Cи, Python, Java, позволяющих решать описанные выше задачи, но, когда работа доходит до этапа формирования концепции, главным аспектом становится оперативность реализации, то есть период времени, который необходим для того, чтобы реализовать алгоритм. И MATLAB, и Octave как раз были спроектированы для решения задач подобного типа, осуществления вычислений и выдачи итоговых результатов на экран монитора.

«Математические вычисления в GNU Octave»
Готовые курсовые работы и рефераты
Консультации эксперта по предмету
Помощь в написании учебной работы

Octave имеет обширный инструментальный набор, предназначенный для решения общих задач численной линейной алгебры, определения корней нелинейных уравнений, интегрирования обычных функций, манипулирования полиномами и интегрирования обыкновенных дифференциальных и дифференциально-алгебраических уравнений. Octave может быть легко расширен пользовательскими функциями, которые могут быть написаны на собственном языке данной программы или, при помощи динамически загружаемых модулей, сформированные на C/C++, Fortran и иных языках.

Знакомство с MATLAB (GNU Octave) (лаб. работа)

Возможны следующие варианты применения данного языка программирования:

1. Изучение и проектирование концептов на производстве, а также и в академических направлениях.
2. Возможность получить аналогичный по функциональному набору MATLAB программный продукт, но который является бесплатным.
3. Возможность разработки и тестирования математических алгоритмов.

В качестве практического использования программы Octave можно привести следующие реальные примеры:

1. NASA применяет Octave при проектировании систем стыковки космических аппаратов.
2. Jaguar использует Octave для анализа данных, получаемых от их болидов Formula 1.
3. Шеффилдский Университет применяет Octave при проектировании программного обеспечения, предназначенного для распознавания раковых клеток.

Как следует из приведенных выше примеров, сфер применения этой программы может быть очень много, и она естественно предоставляет возможность написания программ в оперативном режиме, а также возможность визуализации данных во многих сферах и направлениях.

Программа Octave способна поддерживать следующий набор арифметических операций:

1. Операцию сложения (+).
2. Операцию вычитания (-).
3. Операцию умножения (*).
4. Операцию деления (/).
5. Операцию возведение в степень (^).
6. Операции с натуральными логарифмами/показателями (log, exp),
7. Операции с тригонометрическими функциями (sin, cos, м другими).

Помимо этого, Octave способна работать как с вещественными числами, так и с комплексными (i, j). Также являются предопределенными определенные математические константы, к примеру, число π (pi) и основание натурального логарифма e.

Векторы и матрицы являются базовыми строительными блоками численного анализа. Для того чтобы создать матрицу и сохранить ее в переменной для дальнейшего применения следует использовать следующую команду:

$>>$ A = [ 1, 1, 2; 3, 5, 8; 13, 21, 34 ]

В результате будет выдан такой ответ:

Если выполнить ввод команды, установив в конце символ точка с запятой, то Octave не станет осуществлять вывод матрицы на экран. К примеру, можно создать матрицу на три строки и два столбца, заполненную случайными числами:

А далее для того, чтобы вывести данную матрицу на дисплей, следует просто задать в командном окне имя переменной, в которой она была сохранена:

Приведем примеры выполнения некоторых арифметических операций. Рассмотрим умножение матрицы на скалярную величину:

Далее рассмотрим перемножение двух матриц:

Пример умножения транспонированной матрицы на саму себя:

Далее рассмотрим решение системы линейных уравнений на примере следующего уравнения:

$X_1 + 3X_2 + 5X_3 = 22$

$3X_1 + X_2 + 3X_3 = 14$

$4X_1 + X_2 + 3X_3 = 15$

Сформируем матрицы коэффициентов и свободных членов для данной системы уравнений:

Рисунок 1. Матрицы. Автор24 — интернет-биржа студенческих работ

А затем наберем обе эти сформированные матрицы в Octave и решим систему методом наименьших квадратов при помощи специального оператора левого деления :

$>>$ A = [1 3 5; 3 1 3; 4 1 3];

Последние три цифры выше являются ответом, то есть, решением.

Источник: spravochnick.ru

Высшая математика командной строки — GNU Octave

Как я и обещал, перехожу от обзора программ замены калькулятора к более серьезным инструментам. Если помните схему из предыдущего поста, то во второй категории находились табличные: OpenOffice / LibreOffice сотоварищи. Эту партию мы можем смело пропустить, так как к командной строке она не относится, к тому же, среди читателей Хабра трудно найти человека, который бы в них не разбирался. Поэтому перехожу сразу к третьей категории.

Специализированные математические программы, уровень студент+

На первом месте в этом списке находится Octave , и это не случайность. Исследователи из Университета Мэриленда в США провели сравнительный анализ математических вычислений, используя MATLAB, Octave, SciLab и FreeMat в простом сценарии и в сложном. В первом случае решали систему линейных уравнений а в втором — конечно-разностную дискретизацию уравнения Пуассона в двухмерном пространстве. Основной вывод — GNU Octave справляется с задачами лучше остальных открытых математических пакетов, демонстрируя результат (страницы 23 и 25) сопоставимый с матлабовским.

Но сначала немного исторического контекста, чтобы понять, как закалялись математические программы с открытыми исходниками.

Догнать и перегнать MATLAB

Так сложилось, что коммерческие программы прибежали и первыми застолбили поляну математических вычислений. Уже с конца 1970-х гг. создатель языка программирования Клив Моулер распространяет MATLAB в университетах США, а в 1984-м вместе с двумя компаньонами переписывают его с Фортрана на Си и создают компанию The MathWorks. Примечательно, что ранние версии распространялись с открытым исходным кодом.

Это было-было, а MATLAB , каким мы его знаем сегодня — это ЯП высокого уровня с поддержкой 2D / 3D графики, разнообразными математическими функциями, интерактивной средой программирования, численных расчетов и решения задач. Внешние интерфейсы позволяют ему интегрироваться со сторонними приложениями и языками программирования. Более 1 000 000 инженеров и ученых по всему миру используют MATLAB и платят за это солидную денежку.

С большим опозданием в игру включаются программы с открытыми исходниками. Только в 1990-х появляются математические пакеты GNU Octave, Scilab и вступают в конкуренцию с лидером вычислительного программирования.

Задуманный изначально как программное пособие для проектирования химического реактора и названный в честь профессора химии Октава Левеншпиля, преподававшего автору математического пакета, Octave призван был заменить студентам Техасского Университета сложный в отладке Fortran . Версия 1.0 вышла в свет 17 февраля 1994 г. Проект стабильно развивается, и в июле нынешнего года зарелизился Octave 4.0.3 . Ждем ебилдов .

Основной миссией Octave была, и в обозримом будущем скорее всего так и останется, быть годной заменой MATLAB так же, как OpenOffice/LibreOffice замещает MS Office для тех, кто умеет считать копейку. Собственно, для этого Octave имеет совместимый с MATLAB синтаксис и набор функций. Более того, несовместимость с MATLAB считается багом, однако софтверная Фемида уже имеет подобный прецедент, и это не считается нарушением копирайта. В этой связи, можно считать Octave программным клоном. Правда о полной совместимости пока говорить не приходится, но работа в этом направлении не прекращается.

Octave написан на C++ , используя стандартную библиотеку шаблонов, имеет интерактивный командный интерфейс, поддерживает расширения — динамически загружаемые модули на родном языке или на C, C++, Fortran и др. Так же как и MATLAB , в алгебраических вычислениях Octave использует библиотеки Basic Linear Algebra Subroutines (BLAS) и Linear Algebra Package (LAPACK).

Установка

Установка Octave в Linux ничем не отличается от установки других программ. На Gentoo Linux запускаем:

$ sudo emerge -av octave

Дебианщики делают то же самое с помощью apt .

$ sudo aptitude install octave

Для SUSE и Arch тоже все очень просто, а вот пользователям Красной Шапки и CentOS придется чуток повозиться. Попытка установить Octave легким движением кисти завершается ошибкой, пакет в репозитариях не найден.

Благо, есть обходной путь. Нужно сперва установить пакет epel-release.

И только после этого yum install octave сработает.
Наконец, все готово и программа установлена.

Операции с матрицами

Не будем терять время и делать операции, которые можно повторить с помощью bc и awk , о ктоторых речь шла в прошлый раз. Поиграемся немного с матрицами.

Сперва простое транспонирование матрицы:

octave:1> A=[1 3 5; 2 4 6] A = 1 3 5 2 4 6 octave:2> A’ ans = 1 2 3 4 5 6

Попробуем решить систему линейных уравнений:

x + y + z = 9 2x + 4y — 3z = 1 3x + 6y — 5z = 0

Вбиваем матрицу A, вектор b и решаем уравнение Ax = b в матричном виде

octave:1> A=[1 1 1; 2 4 -3; 3 6 -5] A = 1 1 1 2 4 -3 3 6 -5 octave:2> b=[9; 1; 0] b = 9 1 0 octave:3> x=Ab x = 7.00000 -1.00000 3.00000

Находим детерминант и собственные значения матрицы.

octave:4> det (A) ans = -1.00000 octave:5> eig (A) ans = -2.88897 2.76372 0.12525

Комплексные числа тоже поддерживаются в вычислениях.

octave:6> A=[-3 0 2; 1 -1 0; -2 -1 0] A = -3 0 2 1 -1 0 -2 -1 0 octave:7> x=det (A) x = -6 octave:8> y=eig(A) y = -1.00000 + 1.41421i -1.00000 — 1.41421i -2.00000 + 0.00000i

Функции и переменные

В Octave переменные и функции создавать гораздо проще, чем, к примеру, в Java или C. На примере матриц, мы уже видели как объявлять переменные. Создания новой функции имеет следующий синтаксис

function [res1, res2, . resM] = имя_функции (arg1, arg2, . argN) тело функции endfunction

Как правило, новую функцию создают либо в отдельном файле, либо в скрипт-файле Octave
до первого ее вызова. Если предполагается использовать пользовательскую функцию в разных скрипт-файлах, то, конечно, предпочтительно создать ее в отдельном файле. В GNU Octave файлы с функциями имеют расширение .m и загружаются автоматически. Имя файла должно строго совпадать с именем функции.

Напишем функцию для решения квадратичного уравнения ax² + bx + c = 0

octave:9> function [x1,x2] = quadr(a, b, c) > D = sqrt(b^2-4*a*c); > x1 = (-b-D)/(2*a); > x2 = (-b+D)/(2*a); > endfunction octave:10> [y1,y2]=quadr(a, b, c) y1 = 2 y2 = 3

Графический интерфейс

Вообще-то, мы тут за математику командной строки гутарим, но пока непонятно как вывести на экран график функции. Впрочем, никакого секрета тут нет — для этих целей используется Gnuplot . Так можно изобразить Аттрактор Лоренца, установив дополнительный пакет odepkg .

Наиболее удобной графической оболочкой для работы с Octave является программа QtOctave . Последняя уже стабилизировалась и включена в состав пакета с момента выхода Octave 4.0 .

Что-же дальше?

Может возникнуть вопрос: а зачем вообще нужны открытые математические пакеты? Офисные приложения нужны всем, но ведь далеко не каждому необходимо сидя дома решать уравнения Пуассона, с помощью преобразования Лапласа. Для ВУЗ-ов MATLAB стоит значительно дешевле, нежели для физических лиц и коммерческих организаций. Коммерческие организации, если будет нужно, найдут денежные средства, а обычные люди пусть занимаются математикой в университетах или считают столбиком.

Конечно же, это ошибочное мнение. Научные расчеты, выполненные с использованием открытого ПО имеют дополнительный «уровень защиты», ведь при желании любой может повторить прогнать те же самые расчеты и проверить валидность результатов. Те же самые вычисления, выполненные на дорогущем ПО, частично отсекают возможность проверки результатов.

Проблема на самом деле гораздо шире (английский текст) и дело не только в открытых или проприетарных математических программах. Не секрет, что научные журналы как правило не требуют от авторов предоставить данные и методику, достаточные для гарантированного повтора результатов эксперимента, проверки модели. Особенно часто этим грешат экономисты и финансисты, попросту засекречивая свои данные. Проверка расчетов и выводов среди выборки из массива статей с «засекреченными» данными дала неожиданные результаты (английский текст). Наука, как и софт, должна быть открытой, вот почему открытые математические пакеты имеют ценность для всего общества.

Рекомендуется к прочтению

Кроме последней книги, остальные материалы, использованные в статье, можно без труда найти в интернете. Половина из приведенных выше ссылок ведут на английские страницы. Буду рад вкратце сообщить о чем идет там речь или помочь с переводом.

• GNU Octave 4.0.1 Manual
• Алексеев Е.Р., Чеснокова О.В GNU Octave для студентов и преподавателей, 2011
• Н. Б. Шамрай Краткое руководство по работе с пакетами GNU Octave и Gnuplot, 2011
• Jesper Schmidt HansenGNU Octave

Источник: habr.com

GNU Octave

GNU Octave — система для работы с математическими вычислениями, поддерживающая MATLAB.

GNU Octave позиционируется как более простая и бесплатная альтернатива программе MATLAB. Это ПО станет полезным как студентам, изучающим точные науки, так и тем, кто занимается математикой профессионально. Программа написана на языке C++, что позволяет внедрять ее во многие другие проекты.

Интерфейс программы командный, в нем можно выполнять математические задачи (линейные и нелинейные), проводить сложные численные эксперименты, решать уравнения, в том числе и дифференциальные. Инструменты программы позволяют работать с графиками в трехмерном интерфейсе. Язык Octave оперирует матрицами, вычисляет корни, поддерживает работу с полиномами.

Одно из достоинств — поддержка расширений. Используя расширения, список возможностей GNU Octave можно существенно расширить. Дополнительные модули можно загружать из официального каталога Octave Forge. Есть также возможность разрабатывать свои дополнения, используя языки программирования C++ или Forge.

Скачать MultiSetup
безопасно с помощью MultiSetup или ниже по прямой ссылке с сервера

Преимущества и недостатки

• Интерактивный командный интерфейс
• Поддержка расширений
• Поддержка проектов MATLAB

• Не всегда корректно работает с кодировкой UTF-8

Источник: ktonasoft.ru

GNU Octave

GNU Octave — это программа на тот случай, если вам требуется инструмент для математических вычислений, рекомендуем скачать GNU Octave. Программа позволяет решать линейные, нелинейные уравнения и другие числовые задачи. Возможности утилиты, интерфейс и синтаксис схожи с известной средой для проведения компьютерных матричных расчетов — Matlab.

Однако главное отличие программ состоит в легальности и безвозмездности использования первого варианта. Разработан GNU Octave для Windows и совместим с сериями XP, Vista, Win 7, 8 и 10. Приложение устанавливается без вирусов и надоедливой рекламы. Занимает до 184 Мб свободного пространства, поэтому, перед тем как загрузить GNU Octave на компьютер, стоит проверить наличие достаточного места на жестком диске.

Операции, которые выполняет продукт

• арифметические расчеты с использованием комплексных и вещественных скаляров и матриц;
• вычисление нелинейных алгебраических уравнений с корнями;
• манипулирование полиномами;
• решение линейных задач;
• интеграция дифференциальных и дифференциально-алгебраических уравнений первого порядка;
• интегрирования функций на конечных и бесконечных интервалах.

Список доступных опций легко дополнить дополнительными конфигурациями из каталога расширений — Octave Forge.

На нашем сайте можно скачать бесплатно GNU Octave для компьютера, без регистрации профиля пользователя.

Источник: freesoft.ru

Общие сведения, установка

Курс посвящен GNU Octave — одной из самых интересных прикладных программ для решения инженерных и математических задач.

GNU Octave — это свободный интерпретирующий язык для проведения математических вычислений. По возможностям и качеству реализации интерпретатора язык Octave можно сравнивать с проприетарной программой MATLAB, причём синтаксис обоих языков очень схож.

Существуют версии языка для различных дистрибутивов GNU Linux ( ALT Linux, Debian, Ubuntu, Mandriva и др.) и для ОС Windows . На наш взгляд, GNU Octave больше ориентирован на работу в Linux. Работа в ОС Windows возможна, но пользователю Windows надо быть готовым работать с простым текстовым редактором и командной строкой.

Когда авторы начинали знакомиться с GNU Octave, основной проблемой было отсутствие хорошего русскоязычного введения в этот язык. Наша книга является попыткой восполнить этот пробел . Поэтому большое внимание было уделено самому языку (глава 3), операциям с матрицами (глава 5) и графическим возможностям пакета (глава 4).

Наш многолетний опыт преподавания информационных дисциплин в Донецком национальном техническом университете говорит нам о том, что студенту и инженеру наряду с описанием функций, предназначенных для решения той или иной задачи, не лишним будет напомнить и математическую постановку решаемой задачи, а зачастую и численные методы решения задачи. Именно поэтому в ряде глав приведены не только описания функций, но и описаны численные методы решения задач.

Что касается графических оболочек, таких как qtOctave, Xoctave и Kalculus , нами принято решение кратко описать наиболее стабильную из них, qtOctave , а основное внимание в книге уделить собственно языку. Мы считаем, что GNU Octave — это в первую очередь мощный интерпретирующий язык. Зная его, пользователь сможет работать с любой графической оболочкой.

Авторы выражают благодарность компании ALT Linux за многолетнее сотрудничество и возможность издать очередную книгу.

Донецк, апрель 2012

1.1 Принципы работы с интерпретатором

Octave — высокоуровневый интерпретируемый язык программирования , предназначенный для решения задач вычислительной математики. В состав пакета входит интерактивный командный интерфейс ( интерпретатор Octave). Интерпретатор Octave запускается из терминала ОС Linux или из его порта в Windows . После запуска Octave пользователь видит окно интерпретатора (рис. 1.1).

В окне интерпретатора пользователь может вводить как отдельные команды языка Octave, так и группы команд, объединяемые в программы. Если строка заканчивается символом «;», результаты на экран не выводятся. Если же в конце строки символ «;» отсутствует,

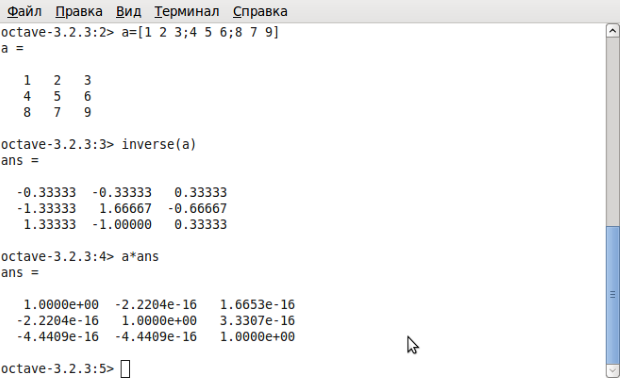
Рис. 1.1. Окно интерпретатора Octave

Рис. 1.2. Использование символов «;» и «%» в Octave

результаты работы выводятся на экран (рис. 1.2). Текст в строке после символа ( процент ) является комментарием и интерпретатором не обрабатывается (рис. 1.2). (Строки комментариев авторы книги будут использовать для пояснения функций и текстов программ.) Рассмотрим несколько несложных примеров.

Пример 1.1. Решить систему линейных алгебраических уравнений (СЛАУ)

Возможны два варианта решения любой задачи в Octave:

1. Терминальный режим. В этом режиме в окно интерпретатора последовательно вводятся отдельные команды.
2. Программный режим. В этом режиме создаётся текстовый файл с расширением .m , в котором хранятся последовательно выполняемые команды Octave. Затем этот текстовый файл (программа на языке Octave) запускается на выполнение в среде Octave.

Для решения СЛАУ в окне интерпретатора Octave последовательно введём следующие команды:

% Определение матрицы коэффициентов системы линейных уравнений. A=[3 5 -7; 3 -4 33; 22 -11 17]; b=[11; 25; 22]; % Вектор правых частей СЛАУ. x=A^(-1)*b % Решение системы методом обратной матрицы. x= 1.56361 2.55742 0.92542 octave -3.2.3:27 > A*x % Проверка. ans = 11.000 25.000 22.000
Листинг 1.1. Решение СЛАУ примера 1.1

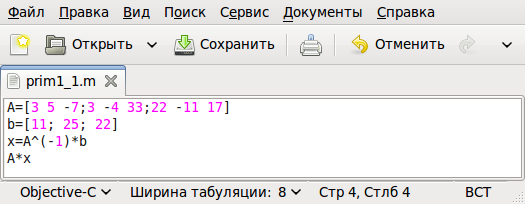
Рис. 1.3. Программа для решения примера 1.1

В переменной хранится результат последней операции , если команда не содержит знака присваивания. Следует помнить, что значение переменной изменяется после каждого вызова команды без операции присваивания.

Теперь рассмотрим, как решить эту же задачу в программном режиме. Вызовем любой текстовый редактор . (Именно текстовый редактор ! Не путайте с текстовыми процессорами типа Microsoft Word или OpenOffice.org/LibreOffice Writer.) Например gedit , в окне которого последовательно введём следующие команды:

A=[3 5 -7; 3 -4 33; 22 -11 17] b =[11; 25; 22] x=A^(-1)*b A*x

Сохраним введённые команды в виде файла с расширением .m , например, /home/evgeniy/prim1_1.m (рис. 1.3). Теперь эту программу необходимо запустить на выполнение из интерпретатора. Для этого в окне интерпретатора введём команды:

cd ’/home/evgeniy’% Переход в каталог, где хранится программа. prim1_1 % Запуск программы.

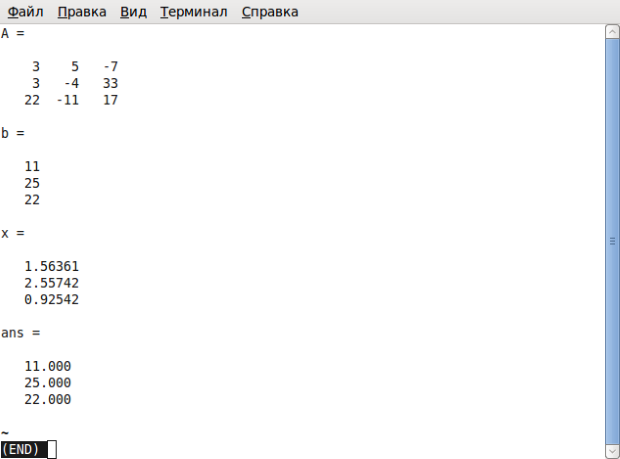
Рис. 1.4. Окно терминала после запуска программы prim1_1

Окно интерпретатора примет вид, представленный на рис. 1.4. Просмотрев результаты работы программы, нажмите для возвращения в режим ввода команд терминала.

Источник: intuit.ru