Применение алгоритма обратного распространения ошибки — один из известных методов, используемых для глубокого обучения нейронных сетей прямого распространения (такие сети ещё называют многослойными персептронами). Этот метод относят к методу обучения с учителем, поэтому требуется задавать в обучающих примерах целевые значения. В этой статье мы рассмотрим, что собой представляет метод обратного распространения ошибки, как он реализуется, каковы его плюсы и минусы.
Сегодня нейронные сети прямого распространения используются для решения множества сложных задач. Если говорить об обучении нейронных сетей методом обратного распространения, то тут пользуются двумя проходами по всем слоям нейросети: прямым и обратным.
При выполнении прямого прохода осуществляется подача входного вектора на входной слой сети, после чего происходит распространение по нейронной сети от слоя к слою. В итоге должна осуществляться генерация набора выходных сигналов — именно он, по сути, является реакцией нейронной сети на этот входной образ. При прямом проходе все синаптические веса нейросети фиксированы.
[DeepLearning | видео 3] В чем на самом деле заключается метод обратного распространения?
При обратном проходе все синаптические веса настраиваются согласно правил коррекции ошибок, когда фактический выход нейронной сети вычитается из желаемого, что приводит к формированию сигнала ошибки. Такой сигнал в дальнейшем распространяется по сети, причём направление распространения обратно направлению синаптических связей. Именно поэтому соответствующий метод и называют алгоритмом с обратно распространённой ошибкой. Синаптические веса настраивают с целью наибольшего приближения выходного сигнала нейронной сети к желаемому.
Общее описание алгоритма обратного распространения ошибки
К примеру, нам надо обучить нейронную сеть по аналогии с той, что представлена на картинке ниже. Естественно, задачу следует выполнить, применяя алгоритм обратного распространения ошибки:
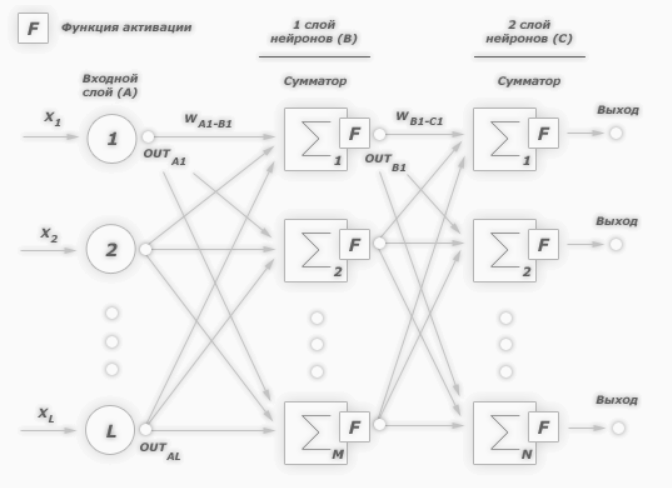

В многослойных персептронах в роли активационной функции обычно применяют сигмоидальную активационную функция, в нашем случае — логистическую. Формула:
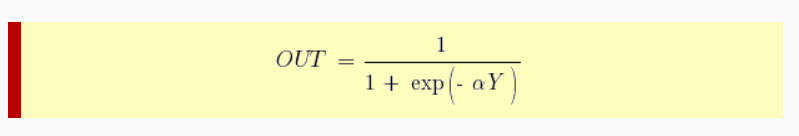
Причём «альфа» здесь означает параметр наклона сигмоидальной функции. Меняя его, мы получаем возможность строить функции с разной крутизной.
Сигмоид может сужать диапазон изменения таким образом, чтобы значение OUT лежало между нулем и единицей. Нейронные многослойные сети характеризуются более высокой представляющей мощностью, если сравнивать их с однослойными, но это утверждение справедливо лишь в случае нелинейности. Нужную нелинейность и обеспечивает сжимающая функция.
Но на практике существует много функций, которые можно использовать. Говоря о работе алгоритма обратного распространения ошибки, скажем, что для этого нужно лишь, чтобы функция была везде дифференцируема, а данному требованию как раз и удовлетворяет сигмоид. У него есть и дополнительное преимущество — автоматический контроль усиления.
Обратное распространение ошибки
Если речь идёт о слабых сигналах (OUT близко к нулю), то кривая «вход-выход» характеризуется сильным наклоном, дающим большое усиление. При увеличении сигнала усиление падает. В результате большие сигналы будут восприниматься сетью без насыщения, а слабые сигналы будут проходить по сети без чрезмерного ослабления.
Цель обучения сети
Цель обучения нейросети при использовании алгоритма обратного распространения ошибки — это такая подстройка весов нейросети, которая позволит при приложении некоторого множества входов получить требуемое множество выходов нейронов (выходных нейронов). Можно назвать эти множества входов и выходов векторами. В процессе обучения предполагается, что для любого входного вектора существует целевой вектор, парный входному и задающий требуемый выход. Эту пару называют обучающей. Работая с нейросетями, мы обучаем их на многих парах.
Также можно сказать, что алгоритм использует стохастический градиентный спуск и продвигается в многомерном пространстве весов в направлении антиградиента, причём цель — это достижение минимума функции ошибки.
При практическом применении метода обучение продолжают не до максимально точной настройки нейросети на минимум функции ошибки, а пока не будет достигнуто довольно точное его приближение. С одной стороны, это даёт возможность уменьшить количество итераций обучения, с другой — избежать переобучения нейронной сети.
Пошаговая реализация метода обратного распространения ошибки
Необходимо выполнить следующие действия: 1. Инициализировать синаптические веса случайными маленькими значениями. 2. Выбрать из обучающего множества очередную обучающую пару; подать на вход сети входной вектор. 3. Выполнить вычисление выходных значений нейронной сети. 4. Посчитать разность между выходом нейросети и требуемым выходом (речь идёт о целевом векторе обучающей пары).
5. Скорректировать веса сети в целях минимизации ошибки. 6. Повторять для каждого вектора обучающего множества шаги 2-5, пока ошибка обучения нейронной сети на всём множестве не достигнет уровня, который является приемлемым.
Виды обучения сети по методу обратного распространения
Сегодня существует много модификаций алгоритма обратного распространения ошибки. Возможно обучение не «по шагам» (выходная ошибка вычисляется, веса корректируются на каждом примере), а «по эпохам» в offline-режиме (изменения весовых коэффициентов происходит после подачи на вход нейросети всех примеров обучающего множества, а ошибка обучения neural сети усредняется по всем примерам).
Обучение «по эпохам» более устойчиво к выбросам и аномальным значениям целевой переменной благодаря усреднению ошибки по многим примерам. Зато в данном случае увеличивается вероятность «застревания» в локальных минимумах. При обучении «по шагам» такая вероятность меньше, ведь применение отдельных примеров создаёт «шум», «выталкивающий» алгоритм обратного распространения из ям градиентного рельефа.
Преимущества и недостатки метода
К плюсам можно отнести простоту в реализации и устойчивость к выбросам и аномалиям в данных, и это основные преимущества. Но есть и минусы: • неопределенно долгий процесс обучения; • вероятность «паралича сети» (при больших значениях рабочая точка функции активации попадает в область насыщения сигмоиды, а производная величина приближается к 0, в результате чего коррекции весов почти не происходят, а процесс обучения «замирает»; • алгоритм уязвим к попаданию в локальные минимумы функции ошибки.
Значение метода обратного распространения
Появление алгоритма стало знаковым событием и положительно отразилось на развитии нейросетей, ведь он реализует эффективный с точки зрения вычислительных процессов способ обучения многослойного персептрона. В то же самое время, было бы неправильным сказать, что алгоритм предлагает наиболее оптимальное решение всех потенциальных проблем. Зато он действительно развеял пессимизм относительно машинного обучения многослойных машин, который воцарился после публикации в 1969 году работы американского учёного с фамилией Минский.
Источник: otus.ru
Back propagation — алгоритм обучения по методу обратного распространения
На предыдущих занятиях мы с вами рассматривали НС с выбранными весами, либо устанавливали их, исходя из определенных математических соображений. Это можно сделать, когда сеть относительно небольшая. Но при увеличении числа нейронов и связей, ручной подбор становится попросту невозможным и возникает задача нахождения весовых коэффициентов связей НС. Этот процесс и называют обучением нейронной сети.
Один из распространенных подходов к обучению заключается в последовательном предъявлении НС векторов наблюдений и последующей корректировки весовых коэффициентов так, чтобы выходное значение совпадало с требуемым:
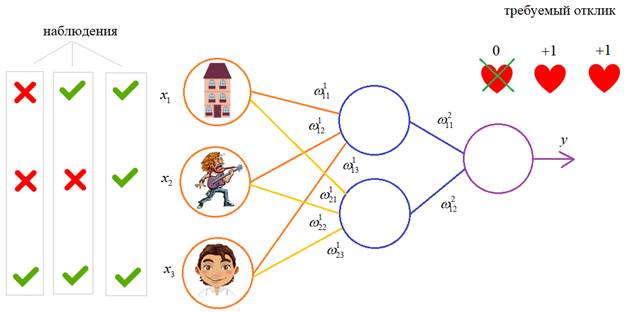
Это называется обучение с учителем, так как для каждого вектора мы знаем нужный ответ и именно его требуем от нашей НС.
Теперь, главный вопрос: как построить алгоритм, который бы наилучшим образом находил весовые коэффициенты. Наилучший – это значит, максимально быстро и с максимально близкими выходными значениями для требуемых откликов. В общем случае эта задача не решена. Нет универсального алгоритма обучения.
Поэтому, лучшее, что мы можем сделать – это выбрать тот алгоритм, который хорошо себя зарекомендовал в прошлом. Основной «рабочей лошадкой» здесь является алгоритм back propagation (обратного распространения ошибки), который, в свою очередь, базируется на алгоритме градиентного спуска.
Сначала, я думал рассказать о нем со всеми математическими выкладками, но потом решил этого не делать, а просто показать принцип работы и рассмотреть реализацию конкретного примера на Python.
Чтобы все лучше понять, предположим, что у нас имеется вот такая полносвязная НС прямого распространения с весами связей, выбранными произвольным образом в диапазоне от [-0.5; 0,5]. Здесь верхний индекс показывает принадлежность к тому или иному слою сети. Также, каждый нейрон имеет некоторую активационную функцию :
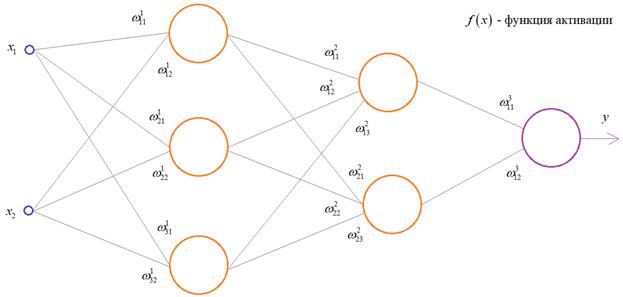
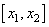
На первом шаге делается прямой проход по сети. Мы пропускаем вектор наблюдения через эту сеть, и запоминаем все выходные значения нейронов скрытых слоев:
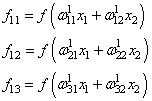
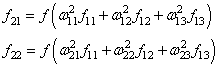
и последнее выходное значение y:
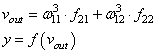
Далее, мы знаем требуемый отклик d для текущего вектора , значит для него можно вычислить ошибку работы НС. Она будет равна:
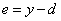
На данный момент все должно быть понятно. Мы на первом занятии подробно рассматривали процесс распространения сигнала по НС. И вы это уже хорошо себе представляете. А вот дальше начинается самое главное – корректировка весов. Для этого делается обратный проход по НС: от последнего слоя – к первому.
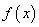
Итак, у нас есть ошибка e и некая функция активации нейронов . Первое, что нам нужно – это вычислить локальный градиент для выходного нейрона. Это делается по формуле:
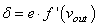
Этот момент требует пояснения. Смотрите, ранее используемая пороговая функция:
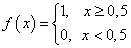
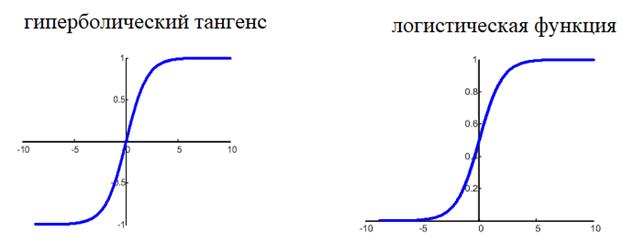
нам уже не подходит, т.к. она не дифференцируема на всем диапазоне значений x. Вместо этого для сетей с небольшим числом слоев, часто применяют или гиперболический тангенс:
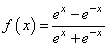
или логистическую функцию:
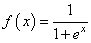
Фактически, они отличаются только тем, что первая дает выходной интервал [-1; 1], а вторая – [0; 1]. И мы уже берем ту, которая нас больше устраивает в данной конкретной ситуации. Например, выберем логистическую функцию.
Ее производная функции по аргументу x дает очень простое выражение:
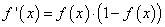
Именно его мы и запишем в нашу формулу вычисления локального градиента:
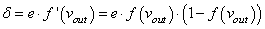
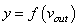
то локальный градиент последнего нейрона, равен:
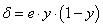
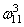
Отлично, это сделали. Теперь у нас есть все, чтобы выполнить коррекцию весов. Начнем со связи , формула будет такой:
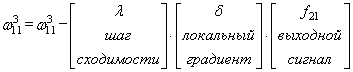
Для второй связи все то же самое, только входной сигнал берется от второго нейрона:
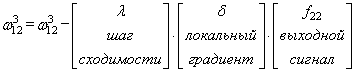
Здесь у вас может возникнуть вопрос: что такое параметр λ и где его брать? Он подбирается самостоятельно, вручную самим разработчиком. В самом простом случае можно попробовать следующие значения:
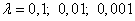
(Мы подробно о нем говорили на занятии по алгоритму градиентного спуска):
Итак, мы с вами скорректировали связи последнего слоя. Если вам все это понятно, значит, вы уже практически поняли весь алгоритм обучения, потому что дальше действуем подобным образом. Переходим к нейрону следующего с конца слоя и для его входящих связей повторим ту же саму процедуру. Но для этого, нужно знать значение его локального градиента. Определяется он просто.
Локальный градиент последнего нейрона взвешивается весами входящих в него связей. Полученные значения на каждом нейроне умножаются на производную функции активации, взятую в точках входной суммы:
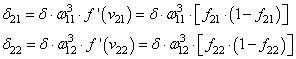
А дальше действуем по такой же самой схеме, корректируем входные связи по той же формуле:
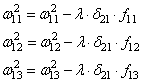
И для второго нейрона:
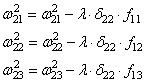
Осталось скорректировать веса первого слоя. Снова вычисляем локальные градиенты для нейронов первого слоя, но так как каждый из них имеет два выхода, то сначала вычисляем сумму от каждого выхода:
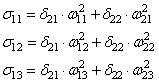
А затем, значения локальных градиентов на нейронах первого скрытого слоя:
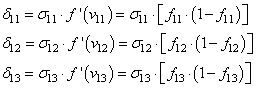
Ну и осталось выполнить коррекцию весов первого слоя все по той же формуле:
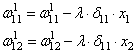
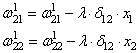
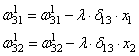
В результате, мы выполнили одну итерацию алгоритма обучения НС. На следующей итерации мы должны взять другой входной вектор из нашего обучающего множества. Лучше всего это сделать случайным образом, чтобы не формировались возможные ложные закономерности в последовательности данных при обучении НС. Повторяя много раз этот процесс, весовые связи будут все точнее описывать обучающую выборку.
Отлично, процесс обучения в целом мы рассмотрели. Но какой критерий качества минимизировался алгоритмом градиентного спуска? В действительности, мы стремились получить минимум суммы квадратов ошибок для обучающей выборки:
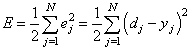
То есть, с помощью алгоритма градиентного спуска веса корректируются так, чтобы минимизировать этот критерий качества работы НС. Позже мы еще увидим, что на практике используется не только такой, но и другие критерии.
Вот так, в целом выглядит идея работы алгоритма обучения по методу обратного распространения ошибки. Давайте теперь в качестве примера обучим следующую НС:
Источник: proproprogs.ru
Метод обратного распространения ошибки: математика, примеры, код
Обратное распространение ошибки — это способ обучения нейронной сети. Цели обратного распространения просты: отрегулировать каждый вес пропорционально тому, насколько он способствует общей ошибке. Если мы будем итеративно уменьшать ошибку каждого веса, в конце концов у нас будет ряд весов, которые дают хорошие прогнозы.
Обновление правила цепочки
Прямое распространение можно рассматривать как длинный ряд вложенных уравнений. Если вы так думаете о прямом распространении, то обратное распространение — это просто приложение правила цепочки (дифференцирования сложной функции) для поиска производных потерь по любой переменной во вложенном уравнении. С учётом функции прямого распространения:
f(x)=A(B(C(x)))
A, B, и C — функции активации на различных слоях. Пользуясь правилом цепочки, мы легко вычисляем производную f(x) по x:
f′(x)=f′(A)⋅A′(B)⋅B′(C)⋅C′(x)
Что насчёт производной относительно B? Чтобы найти производную по B, вы можете сделать вид, что B (C(x)) является константой, заменить ее переменной-заполнителем B, и продолжить поиск производной по B стандартно.
f′(B)=f′(A)⋅A′(B)
Этот простой метод распространяется на любую переменную внутри функции, и позволяет нам в точности определить влияние каждой переменной на общий результат.
Применение правила цепочки
Давайте используем правило цепочки для вычисления производной потерь по любому весу в сети. Правило цепочки поможет нам определить, какой вклад каждый вес вносит в нашу общую ошибку и направление обновления каждого веса, чтобы уменьшить ошибку. Вот уравнения, которые нужны, чтобы сделать прогноз и рассчитать общую ошибку или потерю:
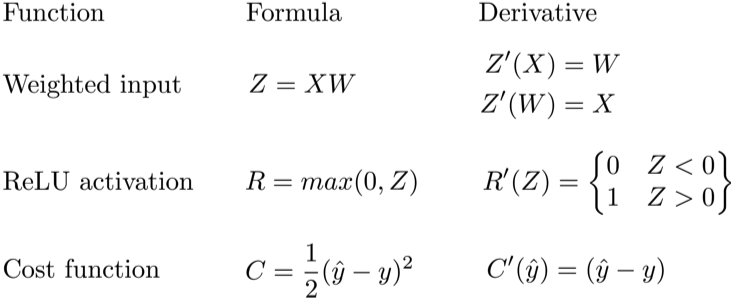
Учитывая сеть, состоящую из одного нейрона, общая потеря нейросети может быть рассчитана как:
Cost=C(R(Z(XW)))
Используя правило цепочки, мы легко можем найти производную потери относительно веса W.
C′(W)=C′(R)⋅R′(Z)⋅Z′(W)=(y^−y)⋅R′(Z)⋅X
Теперь, когда у нас есть уравнение для вычисления производной потери по любому весу, давайте обратимся к примеру с нейронной сетью:
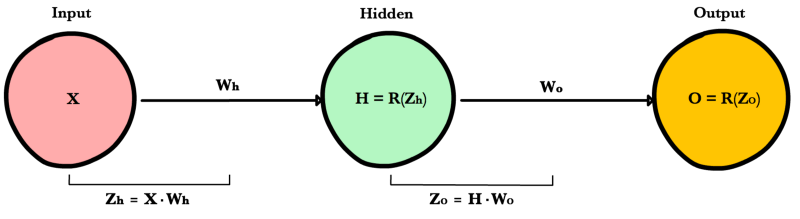
Какова производная от потери по Wo?
А что насчет Wh? Чтобы узнать это, мы просто продолжаем возвращаться в нашу функцию, рекурсивно применяя правило цепочки, пока не доберемся до функции, которая имеет элемент Wh.
И просто забавы ради, что, если в нашей сети было бы 10 скрытых слоев. Что такое производная потери для первого веса w1?
C(w1)=(dC/dy^)⋅(dy^/dZ11)⋅(dZ11/dH10)⋅(dH10/dZ10)⋅(dZ10/dH9)⋅(dH9/dZ9)⋅(dZ9/dH8)⋅(dH8/dZ8)⋅(dZ8/dH7)⋅(dH7/dZ7)⋅(dZ7/dH6)⋅(dH6/dZ6)⋅(dZ6/dH5)⋅(dH5/dZ5)⋅(dZ5/dH4)⋅(dH4/dZ4)⋅(dZ4/dH3)⋅(dH3/dZ3)⋅(dZ3/dH2)⋅(dH2/dZ2)⋅(dZ2/dH1)⋅(dH1/dZ1)⋅(dZ1/dW1)
Заметили закономерность? Количество вычислений, необходимых для расчёта производных потерь, увеличивается по мере углубления нашей сети. Также обратите внимание на избыточность в наших расчетах производных.
Производная потерь каждого слоя добавляет два новых элемента к элементам, которые уже были вычислены слоями над ним. Что, если бы был какой-то способ сохранить нашу работу и избежать этих повторяющихся вычислений?
Сохранение работы с мемоизацией
Мемоизация — это термин в информатике, имеющий простое значение: не пересчитывать одно и то же снова и снова. В мемоизации мы сохраняем ранее вычисленные результаты, чтобы избежать пересчета одной и той же функции. Это удобно для ускорения рекурсивных функций, одной из которых является обратное распространение. Обратите внимание на закономерность в уравнениях производных приведённых ниже.
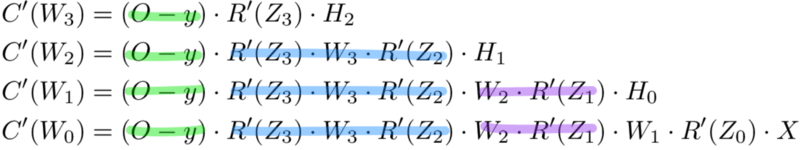
Каждый из этих слоев пересчитывает одни и те же производные! Вместо того, чтобы выписывать длинные уравнения производных для каждого веса, можно использовать мемоизацию, чтобы сохранить нашу работу, так как мы возвращаем ошибку через сеть. Для этого мы определяем 3 уравнения (ниже), которые вместе выражают в краткой форме все вычисления, необходимые для обратного распространения. Математика та же, но уравнения дают хорошее сокращение, которое мы можем использовать, чтобы отслеживать те вычисления, которые мы уже выполнили, и сохранять нашу работу по мере продвижения назад по сети.
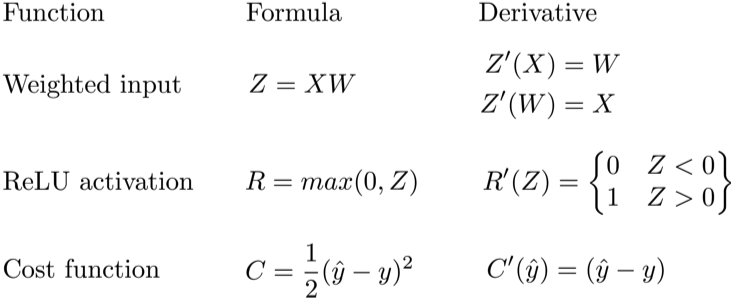
Для начала мы вычисляем ошибку выходного слоя и передаем результат на скрытый слой перед ним. После вычисления ошибки скрытого слоя мы передаем ее значение обратно на предыдущий скрытый слой. И так далее и тому подобное. Возвращаясь назад по сети, мы применяем 3-ю формулу на каждом слое, чтобы вычислить производную потерь по весам этого слоя. Эта производная говорит нам, в каком направлении регулировать наши веса, чтобы уменьшить общие потери.
Примечание: термин ошибка слоя относится к производной потерь по входу в слой. Он отвечает на вопрос: как изменяется выход функции потерь при изменении входа в этот слой?
Ошибка выходного слоя
Для расчета ошибки выходного слоя необходимо найти производную потерь по входу выходному слою, Zo. Это отвечает на вопрос: как веса последнего слоя влияют на общую ошибку в сети? Тогда производная такова:
C′(Zo)=(y^−y)⋅R′(Zo)
Чтобы упростить запись, практикующие МО обычно заменяют последовательность (y^−y)∗R'(Zo) термином Eo. Итак, наша формула для ошибки выходного слоя равна:
Eo=(y^−y)⋅R′(Zo)
Ошибка скрытого слоя
Для вычисления ошибки скрытого слоя нужно найти производную потерь по входу скрытого слоя, Zh.
C′(Zh)=(y^−y)⋅R′(Zo)⋅Wo⋅R′(Zh)
Далее мы можем поменять местами элемент Eo выше, чтобы избежать дублирования и создать новое упрощенное уравнение для ошибки скрытого слоя:
Eh=Eo⋅Wo⋅R′(Zh)
Эта формула лежит в основе обратного распространения. Мы вычисляем ошибку текущего слоя и передаем взвешенную ошибку обратно на предыдущий слой, продолжая процесс, пока не достигнем нашего первого скрытого слоя. Попутно мы обновляем веса, используя производную потерь по каждому весу.
Производная потерь по любому весу
Вернемся к нашей формуле для производной потерь по весу выходного слоя Wo.
C′(WO)=(y^−y)⋅R′(ZO)⋅H