ПО сначала нужно установить с помощью инсталлятора, где нужно выполнить пару простых шагов.
Программу можно запустить двумя способами:
· Перейти в корневую папку, где хранится программа, и запустить исполняемый файл «Registra.exe»;
· Кликнуть по ярлыку, который создает на рабочем столе после установки.
Входные и выходные данные
Входным файлом являются «doctors.xml» и «patients.xml». А также в приложение можно внести эти входные данные:
Выходной информацией программы является талон на прием к лечащему врачу. В талоне указаны эти данные:
· Дата и время приема;
Сообщения
При установке программы будут сообщения:
· Выбор пути для установки;
· Соглашение с условиями пользования;
· Выбор мест, где будут ярлыки программы.
Руководство пользователя
Назначения программы
Эта программа создана для записи больных к врачам. Ею будут пользоваться работники поликлиники для быстрой и удобной записи к врачу и поиска карты пациента.
Как написать деловое письмо, чтобы ответили | Советы по написанию письма с предложением чего-либо
«Регистратура поликлиники» позволяет посмотреть расписание врачей, создать, также записать пациента к доступным врачам.
Условия выполнения программы
Минимальные требования к электронной вычислительной машине:
· Процессор: IntelCeleron или аналогичный AMD;
· Частота: 1500 МГЦ;
· Оперативная память: 512 Мб;
· Клавиатура и мышь.
Рекомендуемые требования к Электронной вычислительной машине:
· Частота: 2000 MHz;
· Оперативная память: 1 ГБ;
· Клавиатура и мышь.
Выполнение программы
Пользователю необходимо запустить программу, после чего выбрать действия:
· Посмотреть расписание врачей;
· Записаться к врачу;
· Выйти из программы.
Рисунок 3.1 Меню программы
Если открыть вкладку расписание врачей, то увидите специальности, затем нужно выбрать кабинет, после чего будет показано доступное время записи к врачу (см. рис. 3.3). Если выбрать другой день и поле выбора времени пусто, значит в этот день врач не принимает людей. Показано на рис. 3.2.
Рисунок 3.2 Недоступное время
Рисунок 3.3 Расписание врачей
Если хотите создать новую карту пациента, то необходимо открыть вкладку «Создание карты», там нужно ввести все данные о пациенте, нажать кнопку «Создать» и подтвердить свое действие (см. рисунок 3.4).
Рисунок 3.4 Создание карты
Для поиска нужно знать хотя бы ФИ или полис. Далее ввести данные в поля (см. рис. 3.5). После чего нажать «поиск». После успешного поиска, выбрать просмотр карты, где вас направят во вкладку «Карты» с данными о найденном пациенте.
API для начинающих. Пример VK. [1/5]
Рисунок 3.5 Поиск
Чтобы записать кого-то к врачу, нужно выбрать пациента, затем выбрать специальность, врача, день приема и время приема. Потом нажать на кнопку «Выбрать» и после этого «Записать пациента» (см. рис. 3.7). После всех процедур будет сформулирован талон в Word, которого можно будет распечатать.
Рисунок 3.6 Сформулированный талон
Рисунок 3.7 Запись
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Найдите 2 минуты и прочитайте про:
Источник: studopedia.ru
2. Обращение к программе-функции Mathcad
Для выполнения программы-функции необходимо обратиться к имени программы-функции с указанием списка фактических параметров (если в описании программы присутствует список формальных параметров), т.е.
< имя — программы >( список фактических параметров )
Фактические параметры указывают, при каких конкретных значениях осуществляются вычисления в теле программы. Фактические параметры отделяются друг от друга запятой.
Очевидно, что между фактическими и формальными параметрами должно быть соответствие по количеству, порядку следования и типу. Последнее соответствие означает:
- если формальным параметром является простая переменная, то в качестве фактического может использоваться константа, переменная, арифметическое выражение;
- если формальным параметром является вектор или матрица, то фактическим должен быть вектор или матрица;
- если формальным параметром является имя встроенной функции или другой программы, то и фактическим параметром должен являться тот же объект.
Замечание Обращение к программе-функции должно находиться после описания программы-функции и к моменту обращенияфактические параметры должны быть определены.Пример 1. Обращение к программе f(x), приведенной на рис. 3 может иметь следующий вид: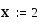 
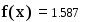
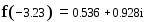
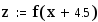
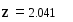Заметим, что переменная z никак не связана с “локальной” переменной z, используемой внутри тела программы-функции. Замечание Передать данные внутрь программы-функции можно используя внутри программы переменные, определенные до описания программы-функции. Например: Вызов программы Берется значение равное 2 
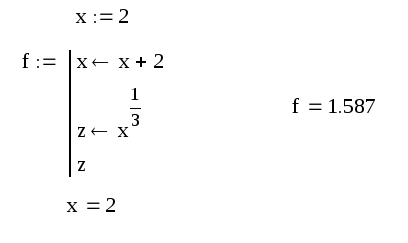Хотя значение переменной х изменилось внутри программы-функции, вне описания программы-функции эта переменная сохранила свое прежнее значение. Замечание Имена фактических параметров при вызове программы-функции могут не совпадать с именами ее формальных параметров.
3. Программирование в программе-функции линейных алгоритмов
Под линейным алгоритмом понимается вычислительный процесс, в котором необходимые операции выполняются строго последовательно. Операторы, реализующие этот алгоритм в теле программы — функции также размещаются последовательно и выполняются все, начиная с первого оператора и кончая последним. Пример 2. Оформим в виде программы-функции вычисление корней квадратного уравнения ax 2 + bx +c = 0 по формуле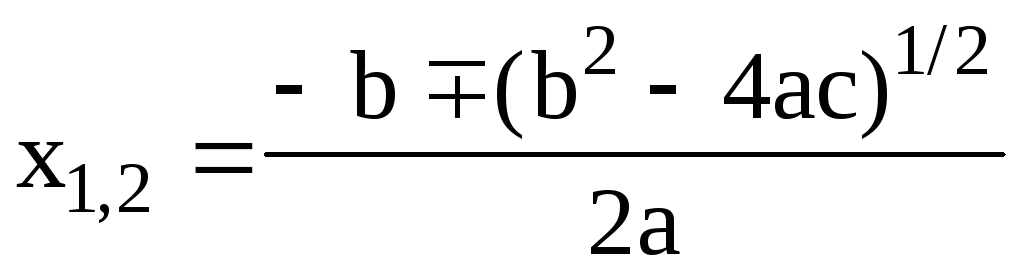 
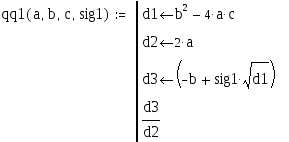Программа qq1 имеет четыре параметра: смысл первых трех понятен, а четвертый определяет знак перед корнем квадратным — задавая Sig1=1, получаем корень x1; Sig1= — 1, получаем корень x2. Программа реализует линейный алгоритм — все операторы выполняются всегда строго последовательно.
4. Программирование в программе-функции разветвляющихся алгоритмов
В разветвляющихся алгоритмах присутствует несколько ветвей вычислительного процесса. Выбор конкретной ветви зависит от выполнения (или невыполнения) заданных условий на значения переменных алгоритма.
Пример 3. Переменная y задается следующим выражением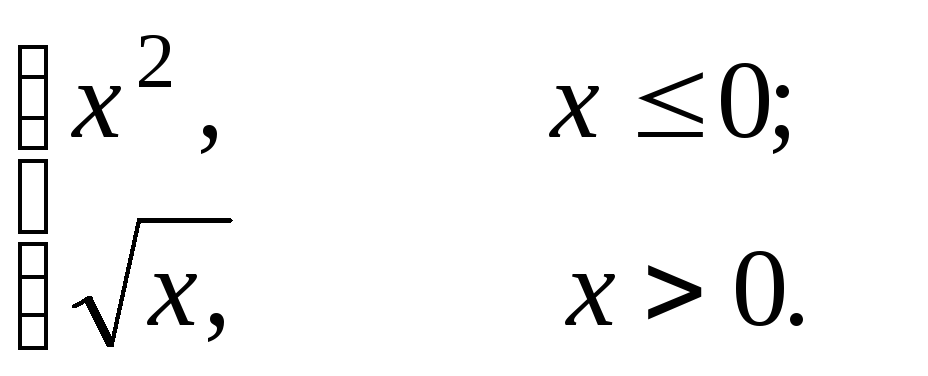 
y(х) = Видно, что алгоритм вычислений содержит две ветви и выбор зависит от значения переменной x. Для программирования разветвляющихся алгоритмов в Mathcad имеется условная функция if и условный оператор. Используя эти конструкции можно «изменить» последовательное выполнение операторов.
В этих конструкциях могут использоваться следующие новые понятия. Выражения отношений. Эти выражения используются для сравнения двух арифметических выражений между собой. Выражение отношений записываются в виде : < выр. А >< знак отношения >< выр.
В>, где в качестве знака отношения выступают символы, приведенные в таблице 1. Если заданное отношение выполняется, то выражение отношений принимает значение равное 1 ( «истина» ), в противном случае — 0 ( «ложь»).
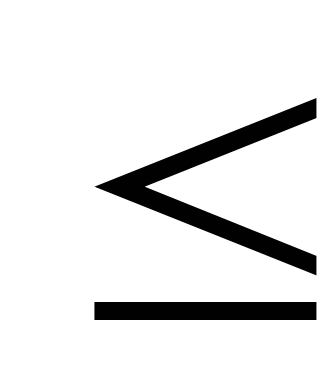
| Знак отношения | Вводимые символы |
| = | [ Ctrl ] + [ = ] |
| [ < ] | |
| > | [ > ] |
|
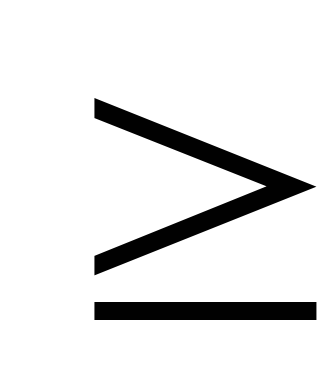
[ Ctrl ] + [ 0 ] |
 |
[ Ctrl ] + [ 9 ] |
 |
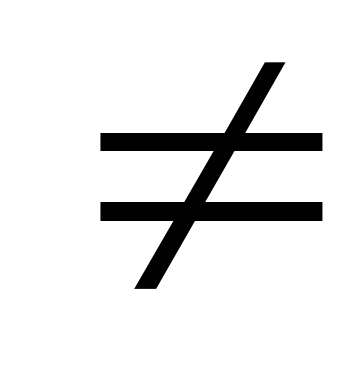[ Ctrl ] + [ 3 ] |
Таблица 1 Пример 4. Вычисление выражения отношений Результат вычисления выражения отношений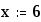
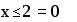В отличие от языков программирования можно сразу в одном выражении проверять несколько условий путем добавления знаков отношений и арифметических выражений. Эту возможность иллюстрирует следующий пример.
Пример 5.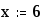
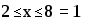Логические операции. Определены две логических операции, которые ставятся между выражениями отношений. Логическая операция ИЛИ. Обозначается знаком + и записывается в виде < логич.выр.1 >+ < логич.выр.
2>Результат операции равен 0, если оба логических выражения равны 0 и равен 1 для всех остальных значений логических выражений. Логическая операция И. Вводится знаком * ( в тексте это точка ) и записывается в виде < логич.выр.1 >. < логич.выр. 2>Результат равен 1, если оба логических выражения равны 1 и равен 0 для всех остальных значений логических выражений Логическое выражение.
Логическим выражением называется конструкция, составленная из выражений отношений, знаков логических операций и круглых скобок. Значение логического выражения вычисляется слева направо с учетом известного правила о приоритете операций. Список приоритетов ( по их убыванию ):
- круглые скобки;
- логическая операция И;
- логическая операция ИЛИ.
Условная функция if. Эта функция записывается в виде : if ( < логич. выраж. >, < ариф.выраж.1>, < ариф.выраж.2 >) Правило вычисления условной функцииif : если логическое выражение равно 1, то функция принимает значение равное значению арифметического выражения 1; если логическое выражение равно 0, то функция принимает значение равное значению арифметического выражения 2. Условная функция используется в арифметических выражениях, стоящих в правой части локального оператора присваивания.
Пример 6. Реализуем алгоритм вычисления функции y(х) примера 3 в виде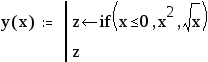 
Обращение к этой программе-функции в тексте документа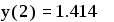 
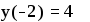
Условный оператор. Этот оператор используется только в теле программы-функции и для его ввода необходимо щелкнуть на кнопке if панели программирования. На экране появляется конструкция с двумя полями ввода, изображенная на следующем рисунке. Поле 2 Поле 1 
В поле 2 вводится логическое выражение (в простейшем случае это выражение отношений). В поле 1 вводится выражение (как правило, арифметическое), значение которого используется, если проверяемое логическое выражение принимает значение 1. Например: Поле 2 Поле 1 Поле 3 
- заключить это поле в выделяющую рамку;
- щелкнуть на кнопке “otherwise” панели программирования;
- в оставшемся поле введите соответствующее выражение.
Пример 7. Составим программу-функцию, вычисляющую функцию y(x), заданную в примере 3. Для этого введем описание следующей программы-функции: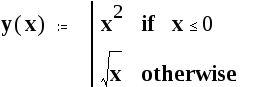 
Обращение к этой программе-функции имеет вид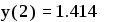 
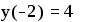Таким образом, выражение, стоящее перед словом otherwise выполняется только в том случае, если не выполнено заданное перед этим условием. В программе можно использовать несколько следующих друг за другом условных операторов с одним выражением перед словом otherwise. Пример 8. Составим программу-функцию для вычисления переменной z по формуле z( t ) = 
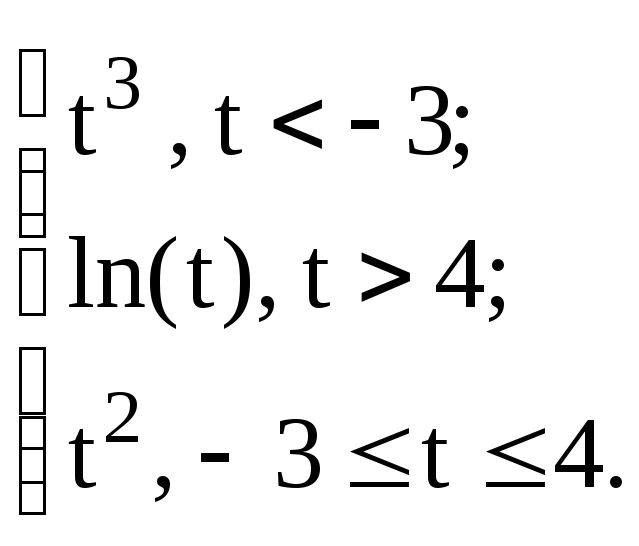В рабочий документ введем описание следующей программы-функции 
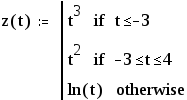Заметим, что функция z(t) получит значение ln(t) только тогда, когда не выполняется условие записанные в двух вышестоящих строках. Обращение к этой программе — функции имеет вид 
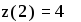Если в поле 3 ввести оператор без слова otherwise, то этот оператор будет выполняться всегда вне зависимости от выполнения выше заданных условных операторов.
Источник: studfile.net
Обращение к подпрограммам.
Широко распространена в программах форма повторяемости, когда одна и та же последовательность действий должна выполняться на различных этапах информации. В программах такого рода в различных местах встречаются фрагменты, одинаковые по выполняемым действиям и различающиеся только в значениях исходных данных.
При составлении программы приходиться задавать одну и ту же группу операторов, соответствующую каждому из повторяющихся фрагментов. Для более эффективного программирования подобных повторений в языке введено понятие подпрограммы. Повторяющаяся группа операторов оформляется в виде самостоятельной единицы – подпрограммы, записывается однократно, а в соответствующих местах программы обеспечивает лишь обращение к ней. Использование аппарата подпрограммы позволяет сократить объем и улучшить структуру программы с точки зрения наглядности и читаемости. Подпрограмма может быть рассмотрена как самостоятельная программа (со своими входными и выходными данными).
В языке Паскаль подпрограммы реализуются в виде процедур и функций, которые вводятся в программу с помощью своего описания.
Описание процедуры.
Процедуры описываются в специальном разделе описательной части программы вслед за разделом переменных.
где PROCEDURE – служебное слово, ИМЯ – имя процедуры, СПИСОК ПАРАМЕТРОВ — перечень имен для обозначения исходных данных и результатов работы процедуры с указанием их типов. Параметры, перечисленные в списке, называются формальными. Допускается описание процедуры, несодержащей формальных параметров:
Содержательная часть процедуры представляет собой блок и состоит, следовательно, из раздела описаний (меток, констант, типов, переменных, процедур, и функций) и раздела операторов, представляющего собой составной оператор BEGIN – END. Заканчивается блок процедуры точкой с запятой.
Пример: Оформить в виде процедуры алгоритм вычисления степени y=x n c натуральным показателем n.
PROCEDURE STEP1(N:INTEGER;X:REAL;VAR Y:REAL;)
VAR I:INTEGER;
FOR I:=1 TO N DO
В заголовке процедуры с именем STEP1 перечислены параметры X, N, определяющие исходные данные процедуры, и параметр Y, обозначающий значение исходной степени – результат выполнения процедуры. Указан также тип всех формальных параметров.
Если в заголовке процедуры параметры указаны без слова VAR, то это параметры-значения. Параметры-значения могут изменяться внутри процедуры, но для внешней программы это изменение окажется незамеченным.
Для получения результатов в основной программе используются параметры-переменные. Эти параметры перечисляются после служебного слова VAR с обязательным указанием типа.
Тело процедуры состоит:
1) из описательной части, где определена переменная I, необходимая и имеющая смысл только внутри данной процедуры и называемая локальной переменной (значение локальной переменной недоступно в основной программе);
2) из составного оператора BEGIN-END, реализующего алгоритм вычисления степени действительного числа с натуральным показателем.
Это то же вычисление оформим в виде процедуры без параметров:
PROCEDURE STEP2;
VAR I:INTEGER;
FOR I:=1 TON DO Y:=Y*X;
В этом случае процедура STEP2 не содержит списка формальных параметров и работает с локальной переменной I, описанной в блоке процедуры, и переменными X, N, Y называются глобальными по отношению к процедуре STEP2. Значение глобальных переменных доступны и могут быть использованы в любой точке основной программы (в частности, внутри данной процедуры).
Функция.
Функция – это подпрограмма, результат выполнения которой есть единственное скалярное значение, присваиваемое имени этой функции. Следовательно, функции являются частным случаем процедур и принципиально отличаются от них тем, что, во-первых, результат выполнения функции – одно значение, а процедуры – одно или несколько; во-вторых, результат выполнения функции передается в основную программу, как значение имени этой функции, а результаты выполнения процедуры – как значения ее параметров.
где FUNCTION – служебное слово, ИМЯ – имя функции, СПИСОК ПАРАМЕТРОВ – перечень формальных параметров (исходных данных) с указанием их типов, ТИП – тип результата: значение, которое должно приобретать имя функции.
Допускается описание функции без параметров:
В содержательной части программы-функции имени должно быть присвоено некоторое значение (значение ответа), т.е. имя хотя бы один раз должно присутствовать в левой части некоторого оператора присваивания.
Пример: Оформить в виде функции алгоритм вычисления степени Y=X n :
FUNCTION STEP3(N:INTEGER; X:REAL) : REAL;
VAR I:INTEGER;
FOR I:=1 TO N DO
STEP3:=Y
В заголовке функции с именем STEP3 перечислены параметры N,X, определяющие ее исходные данные. Результат выполнения функции (значение локальной переменной Y) присваивается ее имени STEP3. Тип результата (тип функции) – REAL, который указывается в заголовке функции при ее описании. Введение локальной переменной Y не обязательно, но придает описанию функции более наглядный вид.
Обращение к подпрограммам.
Описание процедуры (или функции), расположенное в разделе описаний, само по себе никакого действия не вызывает. Чтобы исполнить процедуру (или функцию), необходимо в нужном месте программы поместить обращение к ней. Обращение к процедуре производится с помощью оператора процедуры, имеющего вид:
где ИМЯ – имя процедуры, к которой происходит обращение, СПИСОК АРГУМЕНТОВ – перечень конкретных значений (выражений) и имен, подставляемых на место формальных параметров процедуры при ее выполнении.
При вызове процедуры формальные параметры, указанные в заголовке, заменяются аргументами в порядке их следования: первому слева параметру в списке ставится в соответствие первый аргумент, второму – второй и т.д. Аргументы, перечисленные в операторе процедуры, называются также фактическими параметрами. Число, тип и порядок следования формальных и фактических параметров должно совпадать. Структура программы, содержащей процедуру, имеет вид:
Пример: Cоставить программу вычисления степени Z=A n , где n – целое число и A<>0. Степень с целым показателем определяется следующим образом:
Учитывая, что 1/A n = (1/A) n и используя процедуру STEP1, описанную в пункте 1.1, составим алгоритм рис.1 а), б) и программу.
PROGRAM STEP4;
VAR M:INTEGER;
PROCEDURE STEP1 (N:INTEGER;X:REAL;VAR Y:REAL);
VAR I:INTEGER;
FOR I:=1 TO N DO
IF M=0 THEN Z:=1
ELSE IF M>0 THEN STEP1(M,A,Z)
WRITELN(A:8:3,’В степени ’,M:3,’ равно ’,Z)
В программе оператор процедуры использован дважды, и каждый раз он вызывает из описательной части программы процедуру STEP1. В теле процедуры произойдет замена формальных параметров N,X,Y на фактические M,A,Z первый раз и на M,1/A,Z второй раз. Затем выполняется совокупность действий, предусмотренных операторами процедуры, и в программу будет возвращен результат Z. Возврат осуществляется к оператору программы STEP4, следующему за оператором вызова процедуры. Очень важно понимать суть и механизм замены формальных параметров фактическими.
Формальные параметры – это переменные, фиктивно (формально) присутствующие в процедуре и определяющие тип и место подстановки фактических параметров.
Фактические параметры – это реальные объекты (программы, заменяющие в теле процедуры при ее вызове формальные параметры). Над этими объектами и производятся действия, предусмотренные операторами тела процедуры.
Имена формальных и фактических параметров целесообразно выбирать различными, что сделает программу более наглядной.
Обращение к функции осуществляется аналогично обращению к стандартным функциям (sin, cos, tan и т.д.) и является разновидностью операнда в выражениях в отличие от вызова процедуры, являющегося разновидностью оператора. В этом месте выражения, где это необходимо, записывается имя функции, вслед за которым в скобках перечисляются фактические параметры. Если вызывается функция без параметров, то указывается только ее имя.
Пример: Составить программу вычисления
используя функцию STEP3, описанную в п. 1.2., (A – действительное, n — целое).
PROGRAM STEP6;
VAR M: INTEGER;
FUNCTION STEP3(N: INTEGER; X: REAL): REAL;
VAR M: INTEGER;
FOR I:=1 TO N DO
WRITELN (‘A=’, A, ‘M=’, M);
Z:=STEP3(5,A)+STEP3(5, 1/A);
IF M=0 THEN R:=1
ELSE OF M>0 THEN R:=STEP3(M,A)
ELSE R:=STEP3(M,1/A);
Функция STEP3 вызывается четыре раза для различных значений фактических параметров. Определение фактических и формальных параметров, локальных и глобальных переменных для функций и процедур совершенно идентично.
Процедуры могут работать не только с простыми переменными, но и с массивами. В качестве примера рассмотрим следующую задачу.
Даны два вектора: А, состоящий из трех элементов, и В, состоящий из четырех элементов. Возвести каждый элемент вектора в квадрат и найти сумму элементов. Действия над векторами оформить в виде процедуры.
PROGRAM SUMMA;
TYPE MAX=ARRAY[1..4] OF REAL;
VAR S1, S2: REAL;I: INTEGER;
PROCEDURE PR(N: INTEGER;VAR S: REAL;VAR C: MAX );
VAR I: INTEGER;
FOR I:=1 TO N DO
FOR I:=1 TO 3 DO
FOR I:=1 TO 4 DO
FOR I:=1 TO 3 DO
FOR I:=1 TO 3 DO
Задание
2.1 Из таблицы 1. По номеру варианта взять задание и составить программу, используя подпрограмму- процедуру.
2.2 Из таблицы 2 по номеру варианта взять задание и составить программу, используя подпрограмму FUNCTION.
Таблица 1
| N вар. | Содержание задания |
| 1. | Определить математическое ожидание и дисперсию для четырёх случайных чисел, заданных векторами: A=[0,5; 1,5; 2] b=[6,7; 8; 7,5; 6] C=[0,1; 10; 4] d=[3,2; 5,1] Расчёт математического ожидания и дисперсии производится по следующим формулам: |
| 2. | Определить расстояние от начала координат до точки Р, делящей отрезок с координатами Р= M= в отношении L=3/2 . Расстояние определяется по формуле: , где |
| 3. | Определить расстояние между точками А и В с координатами A=[2;5], B=[2;1], и точками C и D с координатами С=[20;4], D=[12;8]. Расстояние определяется по формуле: , где и |
| 4. | Вычислить значение функции , где корни уравнения ; — корни уравнения . Корни уравнения находятся в подпрограмме- процедуре. Если корни мнимые, то считать их равными нулю. Исходные данные: A=0,5; B=3; C=1; |
| 5. | Заданы стороны двух треугольников АВС (стороны а, в, с) и DEF (стороны d, e, f). Найти сумму и разность площадей треугольников АВС DEF. Площадь треугольника NKM со сторонами n, k, m вычисляется по формуле: r — полупериметр треугольника NKM. Исходные данные: а=3; b=2,5; c=1,7; d=2; e=7,8; f=7 |
| 6. | Три точки заданы своими декартовыми координатами a=, b=, c=. Вычислить полярные координаты этих точек. Полярный радиус r и полярный угол вычисляются по формулам: , |
| 7. | Определить номера точек, лежащих в круге радиусом r. Координаты точек заданы массивами и . Исходные данные: n=6; r=3; i=1,2….n = = |
| 8. | Вычислить значение где заданы массивом; =(0,2; 0,46; 0,33; 0,97; 0,15; 0,61; 0,54; 0,77) |
| 9. | Вычислить значение R= где X= S= элементы массива. Исходные данные:n=3; m=8; i=1,.2..m; =(5,6; 0,3; -0,9; 3; 2,8; 1,45; -4,6; 1) |
| 10. | Определить значение функции Z=sh(x+y) и M=sh(xy), где M изменятся от 1 до 0,5 с шагом 0,1; Y изменяется от 2 до 2,6 с шагом 0,2. Гиперболический синус вычисляется по формуле: |
| 11. | Заданы стороны двух треугольников JKL (стороны j,c,l), иABD(стороны a,b,d).Переменной Sприсвоить значение –1, если площадь треугольника JCLменьше или равна площади треугольника ABD, и значение 1,если площадь треугольника JCL больше площади треугольника ABD. Площадь треугольника MNK со сторонами m,n,k вычисляются по формуле Герона. W= где r-полупериметр треугольника MNK. Исходные данные j=1; c=2,5; i=2,7; a=1; b=2,7; d=3,2. |
| 12. | Построить таблицу Z=ch(x 2 =y 2 ),где имеется от 3до 4 с шагом 0,1, y меняется от 2 до 3 с шагом 0,2. Гиперболический косинус вычисляется по формуле: CH(n)=(e n +e n )/2. |
| 13. | Заданы два квадратных уравнения Ax 2 +Dx+C=0, Dx 2 +Fx+R=0. Найти минимальное значение среди корней этих уравнений. В случае если корни мнимые считать их равными нулю. Решение квадратного уравнения оформить в виде подпрограммы-процедуры. Исходные данные:a=2; b=-5,2; c=1,3; d=3,7; f=1,8; r=6. |
| 14. | Четыре точки заданы своими координатами X=(x1,x2), Y=(y1,y2) Z=(z1,z2), P=(p1,p2) Вычислить и напечатать, сколько из них принадлежит полосе, аналитически заданной неравенством: fMa1+Na2M=5; N=3; f=2,5; r=7,1; X=(-4,2;3); Y=(1,8; 0,8);Z=(-8,6; -4,1); P=(-1; -0,1). |
| 15. | Задана окружность (x-a) 2 +(y-b) 2 =r и две точки P=(p1,p2) и F=(f1,f2).Выяснить и напечатать, сколько точек (нуль,одна или две) лежит внутри окружности. Проверку, лежит ли точка внутри окружности, оформить в виде подпрограммы-процедуры. Исходные данные a=3,2; b=4,1; r=2; p=(6,1; 4,3); f=(27,48;-6) . |
Таблица 2
| N вар. | Содержание задания |
| 1. | при а=4,5; b=0,7; c=6,2; А x принимает значения 0,2; 0,56; 0,83 |
| 2. | , при a=0,8; b=0,16; c=0,4; a=0,6; b=0,4; c=1,2; a=0,47; b=0,1; c=0,5. |
| , при a=0,15; b=1,5; a=1,7; b=0,1. | |
| 4. | , при x=1,4; y=0,8; x=0,9; y=0,6; x=2,9; y=0,4; a d=5,3, при всех значениях x,y. |
| 5. | , при x=0,4; y=1,2; x=0,25; y=1,3; a=0,54; b=1 при всех значениях x, y |
| 6. | , при a=10,7; b=6,3; y=0,35; a x принимает значения 0,6; 0,51; 0,42. |
| 7. | , при x=3; y=4; x=1,6; y=5,8; x=4,5; y=2,7; a=7,1; b=2,4 при всех значениях x, y |
| 8. | , при x=0,1; y=0,7; x=0,4; y=0,6 x=0,5; y=0,2; a=2; b=0,1 при всех значениях x, y |
| 9. | , при a=9,7; b=2,7, a x принимает значения 4,8; 9,6; 0,44. |
| 10. | , при x=0,35; y=0,1; x=0,82; y=0,12; x=0,67; y=0,3, a=0,24; b=4,9 при всех значениях x, y. |
| 11. | , при a=4; b=2,7, a x принимает значения 0,1; 0,25; 0,14; 0,21. |
| 12. | |
| 13. | |
| 14. | |
| 15. |
Источник: megapredmet.ru