Нормальный алгоритм маркова программа

This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.

Switch branches/tags
Branches Tags
Could not load branches
Nothing to show
Could not load tags

Nothing to show

Name already in use

A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?

Cancel Create

• Local
• Codespaces

HTTPS GitHub CLI
Use Git or checkout with SVN using the web URL.
Work fast with our official CLI. Learn more about the CLI.

Sign In Required

Please sign in to use Codespaces.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching Xcode

If nothing happens, download Xcode and try again.

Нормальный алгоритм Маркова — теория и практика

Launching Visual Studio Code

Your codespace will open once ready.

There was a problem preparing your codespace, please try again.

Latest commit

Git stats

Files

Failed to load latest commit information.

Latest commit message
Commit time

README.md

Emulator of turing machine and markov algorithm.

• Нормальные машины Тьюринга
• Пустые слова в НАМ

Установка программы производится через пакетный менеджер pip. Получить последнюю версию можно командой (попробуйте добавить sudo в начало команды, если установка не проходит успешно):

# python3 -m pip install —upgrade turingmarkov

Данная программа работает как интерпретатор или компилятор машины Тьюринга и нормальных алгоритмов Маркова. Простейший способ запустить программу — набрать в консоли:

$ turingmarkov run turing [имя файла].turing $ turingmarkov run markov [имя файла].markov

Где [имя файла] — файл с исходным кодом машины Тьюринга или алгоритма Маркова соответствено. Подробнее про формат файлов читайте ниже.

После этого программа переходит в режим считывания и на каждую введенную строку печатает результат работы алгоритма. Если программа перестала отвечать на запросы, вероятнее всего, алгоритм зациклился на введенной строке. Нажмите ctrl+C для остановки выполнения.

Ограничения: в НАМ пробельные символы игнорируются, МТ не работает для пустых строчек.

Также программа может работать в режиме компилятора и перерабатывать формальное описание алгоритма в программу на Python.

$ turingmarkov compile turing [имя файла].turing $ turingmarkov compile markov [имя файла].markov

Скомпилированный файл преобразовывает каждую строчку со входного потока и выдает результат в выходной. Если алгоритм не применим (не останавливается) к данной строчке, то вторая команда будет выполняться вечно или упадет с ошибкой.

Взаимодействие с системой ejudge

Для установки в систему ejudge:

Нормальный алгоритм Маркова- пример программы.

1. Установите пакет через python3 -m pip install —upgrade turingmarkov .
2. Залогиньтесь под пользователем ejudge.
3. Склонируйте репозиторий с исходными кодами.
4. Находясь в корневом каталоге репозитория, выполните команду make install-ejudge-binding .
5. Выполните команду ejudge-configure-compilers и убедитесь, что компиляторы Turing Machine и Markov Algorithm найдены (показаны их версии).
6. Перезапустите ejudge (через ejudge-control ).

Краткие теоретические сведения

Машина Тьюринга (МТ) — абстрактный исполнитель (абстрактная вычислительная машина). Была предложена Аланом Тьюрингом в 1936 году для формализации понятия алгоритма.

Машина Тьюринга, согласно тезису Чёрча — Тьюринга, способна имитировать все исполнители (с помощью задания правил перехода), каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.

В состав машины Тьюринга входит неограниченная в обе стороны лента, разделённая на ячейки, и управляющее устройство (также называется головкой записи-чтения (ГЗЧ)), способное находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано.

Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки символы некоторого конечного алфавита. Выделяется особый пустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.

Управляющее устройство работает согласно правилам перехода, которые представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Одно из состояний машины Тьюринга помечено как заключительное, и переход в него означает конец работы, остановку алгоритма.

Конкретная машина Тьюринга задаётся перечислением элементов множества букв алфавита A , множества состояний Q и набором правил, по которым работает машина.

Они имеют вид: a[i],q[k] -> a[i1],d[j],q[k1] Если головка находится в состоянии q[k] , а в обозреваемой ячейке записана буква a[i] , то:

1. В ячейку вместо a[i] записывается a[i1] .
2. Головка делает движение d[j] , которое имеет три варианта: на ячейку влево L , на ячейку вправо R , остаться на месте N .
3. Головка переходит в состояние q[k1] .

Для каждой возможной конфигурации q[i],a[j] имеется ровно одно правило. Правил нет только для заключительного состояния, попав в которое машина останавливается. Кроме того, необходимо указать конечное и начальное состояния, начальную конфигурацию на ленте и расположение головки машины.

Работа МТ состоит из однотипных тактов. Каждый такт состоит в выполнении одной команды. Предполагается, что первоначально МТ находится в состоянии 0 . Таким образом, если задать информацию на ленте и положение головки, работа МТ определяется однозначно. Работа МТ считается завершенной, если выполнилась заключительная команда. Полученное последнее cодержимое ленты является результатом работы МТ.

В эмуляторе МТ для обозначения пустого символа используетя знак подчёркивания. Конечное состояние обозначается символом ! .

Для записи правил используется таблица. Каждая строка символизирует состояние. Каждый столбец — обозреваемый символ из алфавита A . На пересечении столбца и строки записана правая часть правила, сотоящая из трех элементов a[i1],d[j],q[k1] , разделенных запятыми. Символ или состояние могут быть пропущены — это означает, что они не меняются.

Если вы уверены, что какой-то комбинации состояние+символ никогда не встретится, можете поставить в соответствующую клетку знак минус — , но тогда машина остановится с ошибкой, если ей будет нужно обработать это правило. Столбцы разделяются пробельными символами. Строки — символом переноса строки.

К непустовму входному слову в алфавите приписать справа букву a .

a b c _ 0 ,R, ,R, ,R, a,N,!

В начале МТ ищет правую границу входного слова, а затем пишет a в пустую ячейку и останавливается.

К числу, записанному в двоичной записи, добавить 1.

0 1 _ 0 ,R, ,R, ,L,1 1 1,N,! 0,L, 1,N,!

В начале МТ ищет правую границу входного слова, а затем переходит в состояние q1 и идёт влево, увеличивая разряды на 1, пока не встретит 0, либо пустой символ _ .

Из входного слова в алфавите удалить все буквы a .

a b c _ # 0 ,R, ,R, ,R, #,L,1 — 1 ,L, ,L, ,L, ,R,2 ,L, 2 _,R, _,R,3 _,R,4 ,R,! _,R,! 3 ,R, ,R, ,R, b,L,1 ,R, 4 ,R, ,R, ,R, c,L,1 ,R,

Так как МТ не позволяет менять некоторую подстроку на другую произвольную подстроку, при решении подобных задач используют приём построения новой копии слова. В начале МТ ставит символ # в конце слова, чтобы разграничить исходное слова от строящегося.

Затем МТ циклически переносит по одному символу из начала входного слова в конец так, чтобы перенеслись все буквы, за исключением букв a . Таким образом, все буквы a просто стираются. По окончании работы МТ удаляет # и останавливается на новом слове. Команда ,R,! в состоянии 2 позволяет избежать зацикливания при пустом входном слове.

Нормальные алгоритмы Маркова

Краткие теоретические сведения

Нормальный алгоритм Маркова (НАМ) — один из стандартных способов формального определения понятия алгоритма. Понятие нормального алгоритма введено А. А. Марковым (младшим) в конце 1940-х годов в работах по неразрешимости некоторых проблем теории ассоциативных вычислений.

НАМ является Тьюринг-полным языком, что делает его по выразительной силе эквивалентным машине Тьюринга и, следовательно, современным зыкам программирования.

Нормальные алгоритмы являются вербальными, то есть предназначенными для применения к словам в различных алфавитах.

Определение всякого нормального алгоритма состоит из двух частей: определения алфавита алгоритма (к словам из символов которого алгоритм будет применяться) и определения его схемы. Схемой нормального алгоритма называется конечный упорядоченный набор так называемых формул подстановки, каждая из которых может быть простой или заключительной.

1. Простыми формулами подстановки называются слова вида L-> D , где L и D — два произвольных слова в алфавите алгоритма (называемые, соответственно, левой и правой частями формулы подстановки).
2. Аналогично, заключительными формулами подстановки называются слова вида L => D , где L и D — два произвольных слова в алфавите алгоритма.

При этом предполагается, что вспомогательные буквы -> и => не принадлежат алфавиту алгоритма (в противном случае на исполняемую ими роль разделителя левой и правой частей следует избрать другие две буквы).

Процесс применения нормального алгоритма к произвольному слову V в алфавите этого алгоритма представляет собой дискретную последовательность элементарных шагов, состоящих в следующем.

Дана входная строка:

1. Проверить формулы в порядке следования сверху вниз, присутствует ли левая часть формулы во входной строке.
2. Если такой формулы не найдено, алгоритм останавливается.
3. Если найдена одна или несколько формул, то самая верхняя из них используется для замены: самое левое вхождение левой части формулы во входной строке заменяется на правую часть формулы.
4. Если только что примененная формула была терминальной, то алгоритм останавливается.
5. Снова переходим к шагу 1.

Заметим, что после применения очередной формулы поиск следующей начинается с самой верхней формулы.

В произвольном слове, состоящем из букв , все подряд стоящие одинаковые буквы заменить одной буквой (например, слово abbbcaa преобразовать в abca ). Схема НАМ. имеет вид:

aa -> a bb -> b cc -> c

Применение этой схемы с слову abbbcaa последовательно даст слова: abbbca , abbca и abca , после чего выполнение НАМ завершится.

Удвоить слово, состоящее из одинаковых символов (для определенности — x ). Т.е. слово x надо преобразовать в xx , слово xx — в xxxx и т.д.

Схема НАМ для этого примера намного сложнее, чем для примера 1. Нельзя написать x -> xx , т.к. в этом случае на каждом шаге НАМ к слову будет добавляться символ x и этот процесс будет бесконечным. Необходимо контролировать удвоение каждого символа слова так, чтобы каждый символ удвоился только один раз. Для это введём маркер, с помощью которого будем обеспечивать контекст применения удваивающего правила.

#x -> xx# # => -> #

Последнее правило вводит «маркер» # (или «курсор»), который с помощью первого правила «перескакивает» через текущий символ слова и удваивает его. Применение этой схемы, например, к слову «xx» последовательно даст слова (в скобках указан номер применяемой формулы подстановки):

(3) #xx (1) xx#x (1) xxxx# (2) xxxx

Дано слово в алфавите . Упорядочить буквы входного слова в лексикографическом порядке.

ba -> ab ca -> ac cb -> bc

1. http://cmcmsu.no-ip.info/1course/alg.schema.mt.htm
2. https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%88%D0%B8%D0%BD%D0%B0_%D0%A2%D1%8C%D1%8E%D1%80%D0%B8%D0%BD%D0%B3%D0%B0
3. https://en.wikipedia.org/wiki/Turing_machine
4. http://cmcmsu.no-ip.info/1course/alg.schema.nam.htm
5. https://ru.wikipedia.org/wiki/%D0%9D%D0%BE%D1%80%D0%BC%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC
6. https://en.wikipedia.org/wiki/Markov_algorithm

Источник: github.com

Пример 1: использование алгоритма Маркова для преобразований над строками

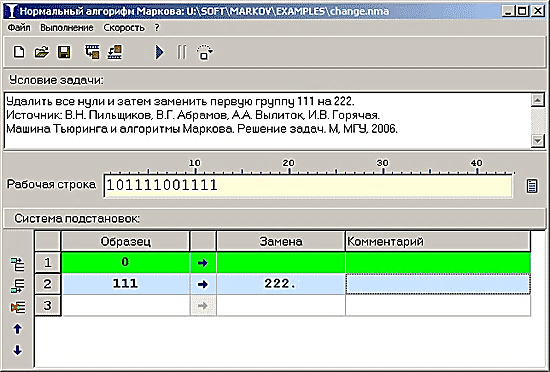
Тренажёр «Нормальные алгорифмы Маркова» это учебная модель универсального исполнителя, предложенного в 1940-х годах А.А. Марковымдля уточнения понятия алгоритма. Марков предположил, что любой алгоритм может быть записан в виде нормального «алгорифма» (учёный считал, что правильно произносить это иностранное слово именно так). Позднее было доказано, что нормальные алгорифмы Маркова эквивалентны по своим возможностям другим универсальным исполнителям:машине Тьюрингаимашине Поста. Нормальный алгорифм задает метод преобразования строк с помощью системы подстановок. Каждая подстановка состоит из слова-образца и слова-замены, разделенных цепочкой символов «->». На каждом шаге замены подстановки просматриваются по порядку сверху вниз, и выполняется первая из них, которая подошла: первое найденное слово-образец рабочей строки заменяется на слово-замену.

1. Программный эмулятор алгоритмов Маркова

Слова слева и справа от знака «->» могут быть (а могут и не быть) заключены в апострофы или двойные кавычки. Следующие подстановки равносильны и определяют замену буквы «а» на сочетание «бв»: а -> бв ‘а’ -> ‘бв’ «а» -> «бв» ‘а’ -> «бв» Левая часть (слово-образец) может отсутствовать, в этом случае слово-замена ставится в самое начало рабочего слова. Обычно такая замена должна стоять последней в списке подстановок (иначе происходит зацикливание). Правая часть подстановки тоже может отсутствовать (при стирании образца). Символ «.» после слова-замены обозначает терминальную подстановку, после которой выполнение алгоритма заканчивается. Например: ‘а’ -> ‘б’. заменить «а» на «б» и остановить программу * -> . стереть знак «*» и остановить программу В верхней части программы находится поле редактора, в которое можно ввести условие задачи в свободной форме. Система постановок, задающая нормальный алгорифм Маркова, набирается в виде таблице в нижней части окна программы. Программа может выполняться непрерывно (F9) или по шагам (F8). Команда, которая сейчас будет выполняться, подсвечивается зеленым фоном. Скорость выполнения регулируется с помощью меню Скорость. Задачи можно сохранять в файлах и загружать из файлов. Сохраняется условие задачи, исходное слово и система подстановок. Протокол работы алгоритма, в котором показаны все последовательные замены, вызывается при нажатии клавиш Ctrl+P.

Источник: studfile.net

Делать Алгоритмы Маркова — это весело

Писать Нормальные Алгоритмы Маркова, это безумно интересно и забавно. Интересно ли узнать о том, как мы делали лучшую в мире IDE для Нормальных Алгоритмов Маркова?

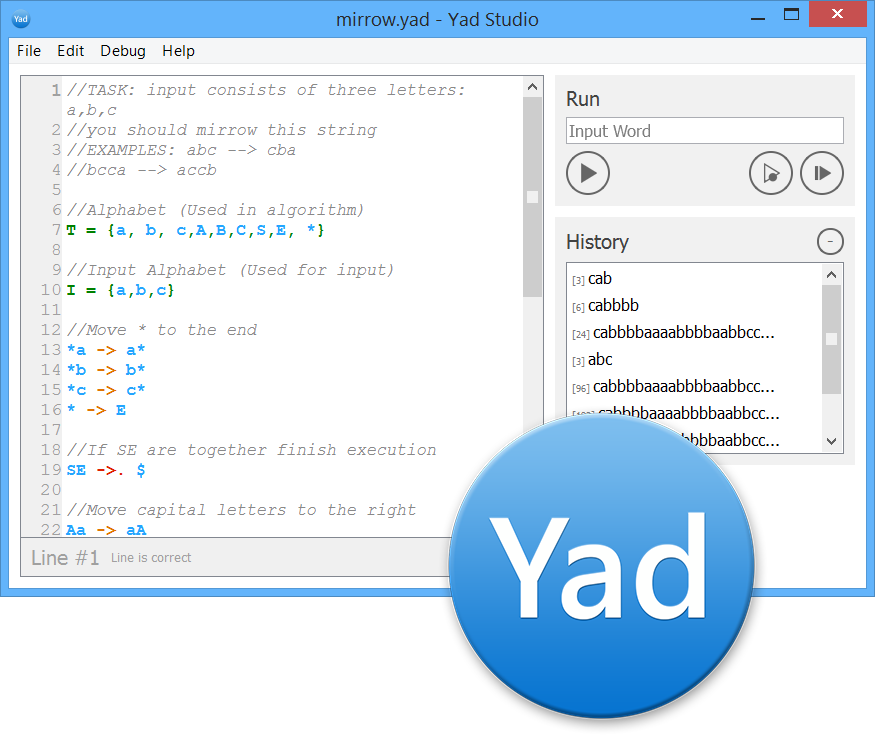
Кому в голову может прийти писать IDE для языка, на котором не написана ни одна коммерческая программа? И нам такая мысль бы не пришла. Но было задание в университете сделать проект — интерпретатор.

Если делать, то сразу лучше всех. Нужно сначала посмотреть, что уже сделали другие. Ничего особо интересного мы не нашли, поэтому очень бегло составили список что должно быть в IDE 21 века:

• Подсветка кода
• Подсказки ошибок
• Комментарии к коду
• Отладчик
• Точки остановки

Было решено сделать все. Писать решили на C++ на Qt. Там GUI без проблем и сигналы-слоты есть. (Потом оказалось, что их можно использовать и без Qt, но это совсем другая история).

Нарисовали маленькую схемку классов

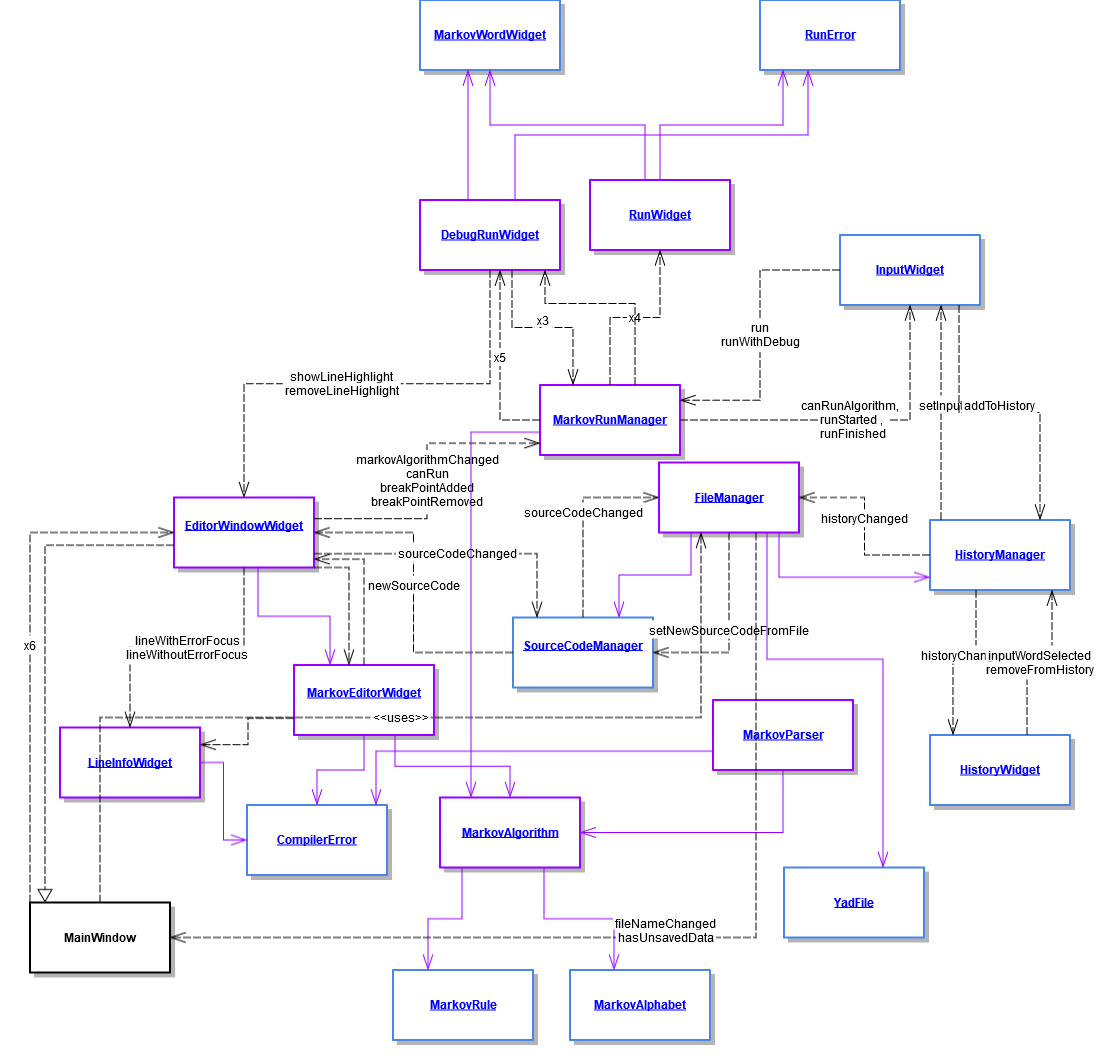
Придумали киллер-фичи

• История запусков — сохраняются все входные слова, для удобного перезапуска. + история хранится также и в самом файле, поэтому она не потеряется при переносе с одного компьютера на другой.
• Пошаговый отладчик. Если поставить точку остановки на любом правиле, то интерпретация остановится, во время выполнения правила, а также покажет, как правило было использовано. После остановки можно продолжить исполнения до следующей точки остановки или начать исполнение пошагово.

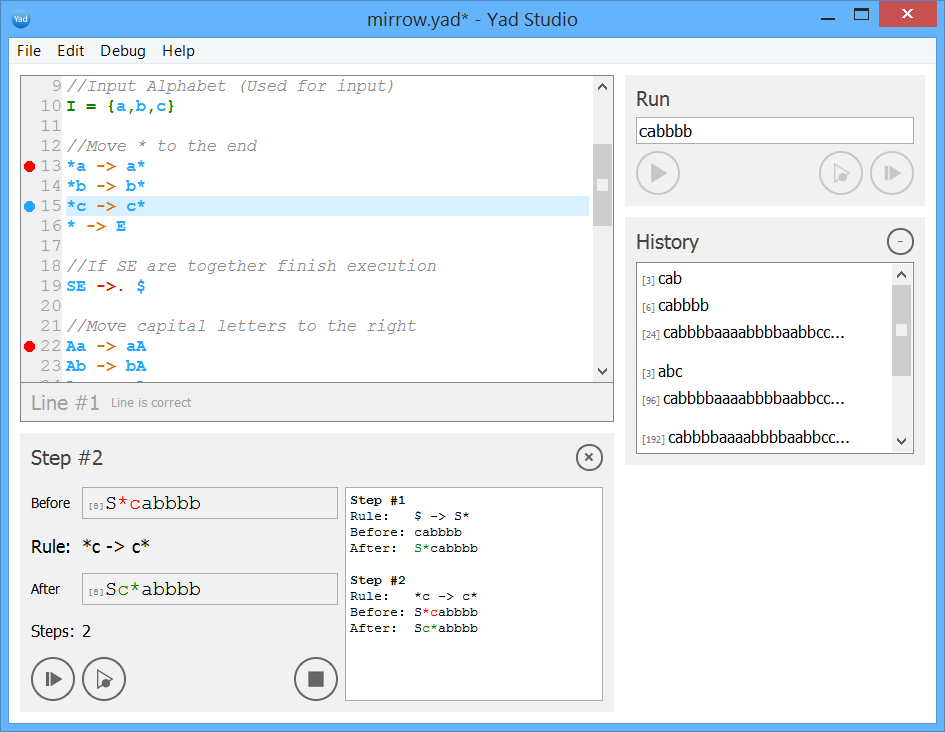
• Редактирование кода не лету — во время отладки можно менять код, который сразу начнет использовать интерпретатор. А также все ошибки и подсказки по их решения появляются сразу при вводе кода.
• Два режима запуска. Быстрый режим — сразу выдает результат, отладочный режим выводит также лог все правил и подстановок, которые были сделаны.
• Предотвращения зацикливаний и программ, которые никогда не завершатся.
• Поддержка дополнительной возможности указать алфавит символов, доступных для написания правил и алфавит символов доступных как входные данные.

Дальше была написана документация всех классов, нарисованы заготовки интерфейса, и началась самая быстрая фаза разработки — кодинг.

Через пару дней бета версия была готова, создан сайт, написана документация, иконки, инсталяшка — все, что нужно для нормального проекта.

Во время первого пилотирования было сделано более 10 улучшений. Самая интересная из них это поддержка «палочек». Как оказалось в Нормальных Алгоритмах Маркова числа удобней всего представлять в виде палочек: ||| = 3, |||| = 4. Для того, чтобы не было необходимости считать их каждый раз мы добавили маленькие цифры, которые это делают за вас.

Интересные решения

Во время разработки мы придумали некоторые интересные решения. Некоторые из них:

• Нам удалось сделать офлайн документацию в браузере, которая автоматически переходит на ее онлайн версию (которая может обновляться в отличии от офлайн), если у человека есть подключение к интернету. Сделали очень просто — подключили javascript файл, который лежит на сервере и делает редирект на онлайн версию. Нет интернета, нет файла, нет перехода — открывается офлайн документация.
• Удобная портативная версия, которая автоматически после запуска делает ассоциацию с .yad файлом, после чего ни чем не отличается от установленной через инсталятор.

Результаты

На проект было потрачено 10 дней, 4 чтобы придумать и написать документацию, 3 чтобы запрограммировать и еще 2 дня на улучшения, документация, сайт.

Теперь все желающие могут скачать без регистрации и СМС с GitHub (пока только для Windows), а также все кто захочет так же сможет собрать из исходников.

Проект мы сделали втроем: dianasi, yuragri и я.

Вместо заключения

Статья про Алгоритмы Маркова без алгоритмов это не серьёзно, вот маленькая программа, которая конвертирует двоичные числа в десятичную систему («палочки»).

//Alphabet T = <|, 0, 1>I = //Rules |0 -> 0|| 1->0| 0->$

P.S. а преподавателю проект не понравился, потому что тут не было базы данных, но это тоже другая история.

Я не уверен, нарушает ли статья правила хабра, про рекламу. Если да, то прошу сообщить или передвинуть в Я пиарюсь.

Источник: habr.com