В данной статье мы применим знания, полученные нами при изучении нейронных сетей перцептрон, и узнаем, как реализовать нейросеть на знакомом языке: Python.
Разработка понятного кода на Python для нейронных сетей
Недавно я просмотрел немало онлайн-ресурсов по нейронным сетям, и, хотя, несомненно, в них есть много полезной информации, я не был удовлетворен найденными мною программными реализациями. Они всегда были или слишком сложными, или недостаточно интуитивно понятными. Когда я писал свою нейронную сеть на Python, я на самом деле хотел сделать что-то, что могло бы помочь людям узнать о том, как работает система, и как теория нейронных сетей переводится на язык программных инструкций.
Однако иногда между ясностью и эффективностью кода существует обратная зависимость. Программа, которую мы обсудим в этой статье, однозначно не оптимизирована для быстрой работы. Оптимизация является серьезной проблемой в области нейронных сетей; реальные приложения могут потребовать огромного количества обучения, и, следовательно, тщательная оптимизация может привести к значительному сокращению времени обработки. Тем не менее, для простых экспериментов, подобных тем, которые мы будем проводить, обучение не займет много времени, и нет оснований делать упор на методиках программирования, которые способствуют скорости, а не простоте и понятности.
ИИ научили писать код | Copilot от GitHub и OpenAI
Полный код программы на Python приведен в конце статьи. Код выполняет как обучение, так и проверку. Данная статья посвящена обучению, а валидацию мы обсудим позже. В любом случае, во фрагменте программы, выполняющем проверку, не так много функционала, который не покрыт во фрагменте, выполняющем обучение.
Размышляя над кодом, вы, возможно, захотите оглянуться на немного сумбурную, но очень информативную диаграмму архитектуры плюс терминологии, которую я представил в части 10.
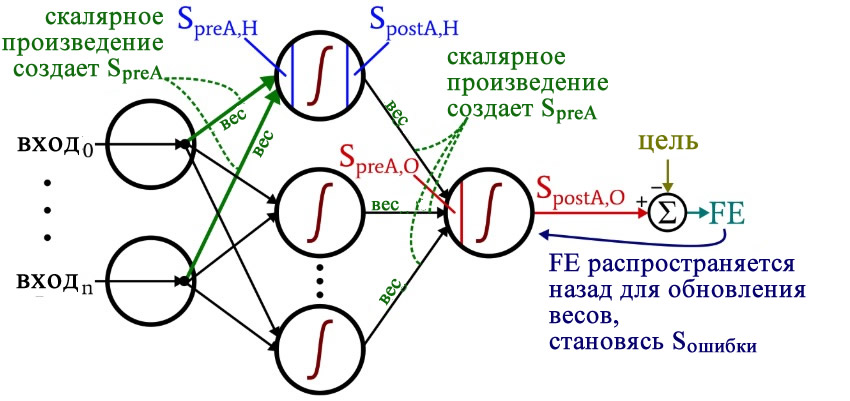
Подготовка функций и переменных
import pandas import numpy as np def logistic(x): return 1.0/(1 + np.exp(-x)) def logistic_deriv(x): return logistic(x) * (1 — logistic(x)) LR = 1 I_dim = 3 H_dim = 4 epoch_count = 1 #np.random.seed(1) weights_ItoH = np.random.uniform(-1, 1, (I_dim, H_dim)) weights_HtoO = np.random.uniform(-1, 1, H_dim) preActivation_H = np.zeros(H_dim) postActivation_H = np.zeros(H_dim)
Библиотека NumPy широко используется для расчетов в нейросети, а библиотека Pandas дает мне удобный способ импортировать данные обучения из файла Excel.
Как вы уже знаете, для активации мы используем функцию логистической сигмоиды. Для расчета значений постактивации нам нужна сама логистическая функция, а для обратного распространения необходима производная логистической функции.
Затем мы выбираем скорость обучения, размерность входного слоя, размерность скрытого слоя и количество эпох. Для реальных нейронных сетей важно обучение в течение нескольких эпох, потому что это позволяет вам извлечь больше информации из ваших обучающих данных. Когда вы генерируете обучающие данные в Excel, вам не нужно запускать несколько эпох, потому что вы можете легко создать больше обучающих выборок.
НЕЙРОСЕТЬ своими руками за 10 минут на Python
Функция np.random.uniform() заполняет наши две матрицы весов случайными значениями от –1 до +1 (обратите внимание, что матрица весов между скрытым и выходным слоями на самом деле представляет собой просто массив, поскольку у нас только один выходной узел). Оператор np.random.seed(1) приводит к тому, что случайные значения становятся одинаковыми при каждом запуске программы. Начальные значения весов могут оказать существенное влияние на конечную производительность обученной сети, поэтому, если вы пытаетесь оценить, как другие переменные улучшают или ухудшают производительность, вы можете раскомментировать эту инструкцию и тем самым устранить влияние случайной инициализации весовых коэффициентов.
И в конце я создаю пустые массивы для значений преактивации и постактивации в скрытом слое.
Импорт обучающих данных
Это та же процедура, которую я использовал в части 3. Я импортирую обучающие данные из Excel, отделяю целевые значения в столбце « output », удаляю столбец « output », преобразую обучающие данные в матрицу NumPy и сохраняю количество обучающих выборок в переменной training_count .
Обработка прямого распространения
Вычисления, которые создают выходное значение, и в которых данные перемещаются слева направо на типовой схеме нейронной сети, составляют фрагмент «прямого распространения» работы системы. Вот код «прямого распространения»:
##################### # обучение ##################### for epoch in range(epoch_count): for sample in range(training_count): for node in range(H_dim): preActivation_H[node] = np.dot(training_data[sample,:], weights_ItoH[:, node]) postActivation_H[node] = logistic(preActivation_H[node]) preActivation_O = np.dot(postActivation_H, weights_HtoO) postActivation_O = logistic(preActivation_O) FE = postActivation_O — target_output[sample]
Первый цикл for позволяет нам проходить через несколько эпох. Внутри каждой эпохи, во втором цикле for , поочередно проходя по выборкам, мы вычисляем выходное значение для каждой выборки (то есть сигнал постактивации выходного узла). В третьем цикле for мы обращаемся индивидуально к каждому скрытому узлу, используя скалярное произведение для генерирования сигнала преактивации и функцию активации для генерирования сигнала постактивации.
После этого мы готовы вычислить сигнал преактивации для выходного узла (снова используя скалярное произведение), и мы применяем функцию активации для генерирования сигнала постактивации. Затем, чтобы вычислить итоговую ошибку, мы вычитаем целевое значение из значения полученного сигнала постактивации выходного узла.
Обратное распространение
После того, как мы выполнили расчеты для прямого распространения, настало время изменить направление. Во фрагменте программы с обратным распространением мы перемещаемся к весам от скрытых узлов к выходному узлу, а затем к весам от входного слоя к скрытому слою, перенося при этом информацию об ошибке для эффективного обучения сети.
for H_node in range(H_dim): S_error = FE * logistic_deriv(preActivation_O) gradient_HtoO = S_error * postActivation_H[H_node] for I_node in range(I_dim): input_value = training_data[sample, I_node] gradient_ItoH = S_error * weights_HtoO[H_node] * logistic_deriv(preActivation_H[H_node]) * input_value weights_ItoH[I_node, H_node] -= LR * gradient_ItoH weights_HtoO[H_node] -= LR * gradient_HtoO
У нас есть два слоя для циклов for : один для весовых коэффициентов между скрытым и выходным слоями и один для весовых коэффициентов между входным и скрытым слоями. Сначала мы генерируем сигнал ошибки (Sошибки, S_error ), который нам нужен для вычисления обоих градиентов, gradient_HtoO (от скрытого слоя к выходному) и gradient_ItoH (от входного слоя к скрытому), а затем мы обновляем весовые коэффициенты, вычитая градиент, умноженный на скорость обучения.
Обратите внимание, как веса между входным и скрытым слоями обновляются внутри цикла для значений между скрытым и выходным слоями. Мы начинаем с сигнала ошибки, который ведет обратно к одному из скрытых узлов, затем распространяем этот сигнал ошибки на все входные узлы, которые подключены к одному конкретному скрытому узлу:
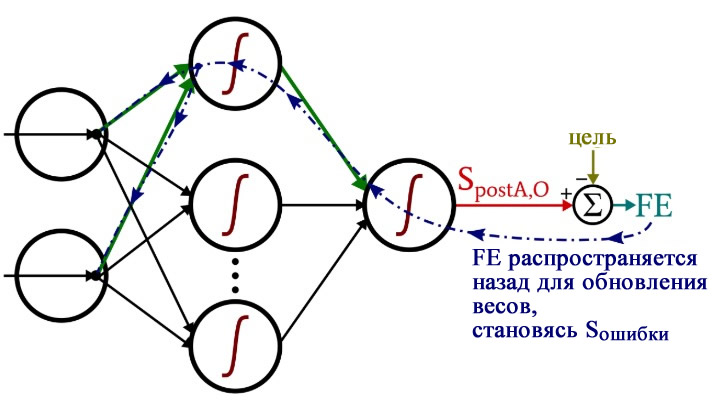
После того, как все весовые коэффициенты (как ItoH (от входного слоя к скрытому), так и HtoO (от скрытого слоя к выходному)), связанные с этим одним скрытым узлом, были обновлены, мы возвращаемся к началу и начинаем снова для следующего скрытого узла.
Также обратите внимание, что веса ItoH модифицируются перед весами HtoO. Мы используем текущий вес HtoO при расчете градиента, поэтому до выполнения расчетов мы не хотим изменять веса HtoO.
Заключение
Интересно задуматься о том, сколько теории ушло в эту относительно короткую программу на Python. Я надеюсь, что этот код на самом деле поможет вам понять, как мы можем программно реализовать нейронную сеть многослойный перцептрон.
Ниже приведен полный код программы.
Источник: radioprog.ru
Пример программы нейронной сети с исходным кодом на с++.
Про нейронные сети хорошо и подробно написано здесь. Попытаемся разобраться как программировать нейронные сети, и как это работает. Одна из задач решаемых нейронными сетями, задача классификации. Программа демонстрирует работу нейронной сети классифицирующей цвет.
В компьютере принята трехкомпонентная модель представления цвета RGB , на каждый из компонентов отводится один байт. полный цвет представлен 24 битами, что дает 16 миллионов оттенков. Человек же может отнести любой из этих оттенков к одному из имеющих название цветов. Итак задача:
Дано InColor — цвет RGB (24 бит )
классифицировать цвет, т.е. отнести его к одному из цветов заданных множеством М = < Черный , Красный , Зеленый , Желтый , Синий , Фиолетовый , Голубой , Белый >.
OutColor — цвет из множества М
Решение номер 1. (цифровое)
Создаем массив размером 16777216 элементов
int8 ColorTab [ 16777216 ];
инициализируем его правильными значениями.
Ответ получаем очень быстро
OutColor = ColorTab [ InColor ];
Решение номер 2. (аналоговое)
напишем функцию, типа
int8 GetColor(DWORD Color)
double Red = (double(((Color>>16)
double Green = (double(((Color>>8)
double Blue = (double((Color
double Level = Red;
if(Green > Level)
Level = Green;
if(Blue > Level)
Level = Blue;
Level = Level * 0.7;
int8 OutColor = 0;
if(Red > Level)
OutColor |= 1;
if(Green > Level)
OutColor |= 2;
if(Blue > Level)
OutColor |= 4;
return OutColor;
>
Это будет работать если задачу можно описать простыми уравнениями, а вот если функция настолько сложна что описанию. не поддается, здесь то на помощь приходят нейронные сети.
Решение номер 3. (нейронная сеть)
Простейшая нейронная сеть. Однослойный перцептрон.
Все нейронное заключено в класс CNeuroNet
#define INCOUNT 3
#define NEUROCOUNTMAX 10
struct Neuron
double x[INCOUNT];// входные сигналы
double w[INCOUNT];// весовые коэффициенты
double w0;// доп вес
double sum;// сумма
double y;// выход аксон
double h;
>;
class CNeuroNet
public:
CNeuroNet(void);
~CNeuroNet(void);
float ActiveSigm(float x);
float ActiveSigmPro(float x);
void ProcNeuro(Neuron
int Process();
int Teach(int Num);
int m_NeuroCount;
Neuron m_Neuro[NEUROCOUNTMAX];
Каждый нейрон имеет 3 входа, куда подаются интенсивности компонент цвета. (R,G, B) в диапазоне (0 — 1) . Всего нейронов 8 , по количеству цветов в выходном множестве. В результате работы сети на выходе каждого нейрона формируется сигнал в диапазоне (0 — 1), который означает вероятность того что на входе этот цвет. Выбираем максимальный и получаем ответ.
Нейроны имеют сигмоидную функцию активации ActiveSigm() . Функция ActiveSigmPro() , производная от сигмоидной функции активации используется для обучения нейронной сети методом обратного распространения.
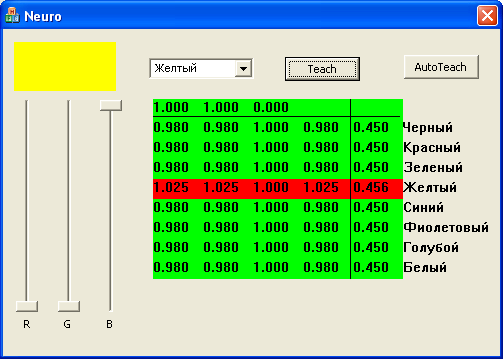
В первой строчке выведены интенсивности цветов. ниже таблица весовых коэффициентов (4 шт. ). В последнем столбце значение на выходе нейронов. Меняем цвет, выбираем из списка правильный ответ, кнопкой Teach вызываем функцию обучения. AutoTeach вызывает процедуру автоматического обучения, 1000 раз, случайный цвет определяется по формуле из решения номер 2, и вызывается функция обучения.
WPF, XPS, NET. Как установить шрифт из памяти
Нейронные сети. Пример программы и исходный код С++.
Deflate. Подробное описание алгоритма декодирование формата Дефлет. Прмер декодирования с пояснениями.
Программирование драйверов для Windows. Общие вопросы программирования драйверов. Какими средствами пользоваться, где скачать DDK.
Программирование RS232 в Windows. СComBase класс для программирования COM порта.
Программирование потоков в Windows. Класс CBaseThread позволяет организовать несколько рабочих потоков.
Динамический Recordset CDynamicRecordSet — класс модернизирует CRecordSet для более удобной работы с БД из MFC приложений.
Как сохранить, восстановить, отредактировать MBR (Master Boot Record), boot sector, нулевой, загрузочный сектор диска при помощи утилиты debug.exe
Источник: www.evmsoft.net
Нейросеть в 11 строчек на Python
Лично я лучше всего обучаюсь при помощи небольшого работающего кода, с которым могу поиграться. В этом пособии мы научимся алгоритму обратного распространения ошибок на примере небольшой нейронной сети, реализованной на Python.
Дайте код!
X = np.array([ [0,0,1],[0,1,1],[1,0,1],[1,1,1] ]) y = np.array([[0,1,1,0]]).T syn0 = 2*np.random.random((3,4)) — 1 syn1 = 2*np.random.random((4,1)) — 1 for j in xrange(60000): l1 = 1/(1+np.exp(-(np.dot(X,syn0)))) l2 = 1/(1+np.exp(-(np.dot(l1,syn1)))) l2_delta = (y — l2)*(l2*(1-l2)) l1_delta = l2_delta.dot(syn1.T) * (l1 * (1-l1)) syn1 += l1.T.dot(l2_delta) syn0 += X.T.dot(l1_delta)
Слишком сжато? Давайте разобьём его на более простые части.
Часть 1: Небольшая игрушечная нейросеть
Нейросеть, тренируемая через обратное распространение (backpropagation), пытается использовать входные данные для предсказания выходных.
Вход Выход 0 0 1 0 1 1 1 1 1 0 1 1 0 1 1 0
Предположим, нам нужно предсказать, как будет выглядеть колонка «выход» на основе входных данных. Эту задачу можно было бы решить, подсчитав статистическое соответствие между ними. И мы бы увидели, что с выходными данными на 100% коррелирует левый столбец.
Обратное распространение, в самом простом случае, рассчитывает подобную статистику для создания модели. Давайте попробуем.
Нейросеть в два слоя
import numpy as np # Сигмоида def nonlin(x,deriv=False): if(deriv==True): return f(x)*(1-f(x)) return 1/(1+np.exp(-x)) # набор входных данных X = np.array([ [0,0,1], [0,1,1], [1,0,1], [1,1,1] ]) # выходные данные y = np.array([[0,0,1,1]]).T # сделаем случайные числа более определёнными np.random.seed(1) # инициализируем веса случайным образом со средним 0 syn0 = 2*np.random.random((3,1)) — 1 for iter in xrange(10000): # прямое распространение l0 = X l1 = nonlin(np.dot(l0,syn0)) # насколько мы ошиблись? l1_error = y — l1 # перемножим это с наклоном сигмоиды # на основе значений в l1 l1_delta = l1_error * nonlin(l1,True) # . # обновим веса syn0 += np.dot(l0.T,l1_delta) # . print «Выходные данные после тренировки:» print l1
Выходные данные после тренировки: [[ 0.00966449] [ 0.00786506] [ 0.99358898] [ 0.99211957]]
Переменные и их описания.
X — матрица входного набор данных; строки – тренировочные примеры
y – матрица выходного набора данных; строки – тренировочные примеры
l0 – первый слой сети, определённый входными данными
l1 – второй слой сети, или скрытый слой
syn0 – первый слой весов, Synapse 0, объединяет l0 с l1.
«*» — поэлементное умножение – два вектора одного размера умножают соответствующие значения, и на выходе получается вектор такого же размера
«-» – поэлементное вычитание векторов
x.dot(y) – если x и y – это вектора, то на выходе получится скалярное произведение. Если это матрицы, то получится перемножение матриц. Если матрица только одна из них – это перемножение вектора и матрицы.
- сравните l1 после первой итерации и после последней
- посмотрите на функцию nonlin.
- посмотрите, как меняется l1_error
- разберите строку 36 – основные секретные ингредиенты собраны тут (отмечена . )
- разберите строку 39 – вся сеть готовится именно к этой операции (отмечена . )
Разберём код по строчкам
import numpy as np
Импортирует numpy, библиотеку линейной алгебры. Единственная наша зависимость.
def nonlin(x,deriv=False):
Наша нелинейность. Конкретно эта функция создаёт «сигмоиду». Она ставит в соответствие любое число значению от 0 до 1 и преобразовывает числа в вероятности, а также имеет несколько других полезных для тренировки нейросетей свойств.
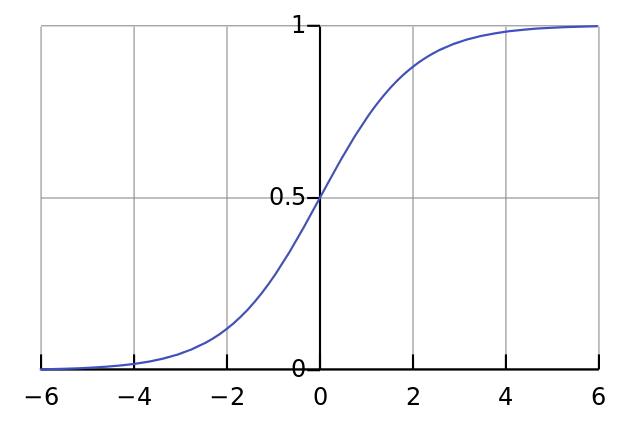
if(deriv==True):
Эта функция также умеет выдавать производную сигмоиды (deriv=True). Это одно из её полезных свойств. Если выход функции – это переменная out, тогда производная будет out * (1-out). Эффективно.
X = np.array([ [0,0,1], …
Инициализация массива входных данных в виде numpy-матрицы. Каждая строка – тренировочный пример. Столбцы – это входные узлы. У нас получается 3 входных узла в сети и 4 тренировочных примера.
y = np.array([[0,0,1,1]]).T
Инициализирует выходные данные. «.T» – функция переноса. После переноса у матрицы y есть 4 строки с одним столбцом. Как и в случае входных данных, каждая строка – это тренировочный пример, и каждый столбец (в нашем случае один) – выходной узел. У сети, получается, 3 входа и 1 выход.
np.random.seed(1)
Благодаря этому случайное распределение будет каждый раз одним и тем же. Это позволит нам проще отслеживать работу сети после внесения изменений в код.
syn0 = 2*np.random.random((3,1)) – 1
Матрица весов сети. syn0 означает «synapse zero». Так как у нас всего два слоя, вход и выход, нам нужна одна матрица весов, которая их свяжет. Её размерность (3, 1), поскольку у нас есть 3 входа и 1 выход. Иными словами, l0 имеет размер 3, а l1 – 1. Поскольку мы связываем все узлы в l0 со всеми узлами l1, нам требуется матрица размерности (3, 1).
Заметьте, что она инициализируется случайным образом, и среднее значение равно нулю. За этим стоит достаточно сложная теория. Пока просто примем это как рекомендацию. Также заметим, что наша нейросеть – это и есть эта самая матрица. У нас есть «слои» l0 и l1, но они представляют собой временные значения, основанные на наборе данных. Мы их не храним.
Всё обучение хранится в syn0.
for iter in xrange(10000):
Тут начинается основной код тренировки сети. Цикл с кодом повторяется многократно и оптимизирует сеть для набора данных.
l0 = X
Первый слой, l0, это просто данные. В X содержится 4 тренировочных примера. Мы обработаем их все и сразу – это называется групповой тренировкой [full batch]. Итого мы имеем 4 разных строки l0, но их можно представить себе как один тренировочный пример – на этом этапе это не имеет значения (можно было загрузить их 1000 или 10000 без всяких изменений в коде).
l1 = nonlin(np.dot(l0,syn0))
Это шаг предсказания. Мы позволяем сети попробовать предсказать вывод на основе ввода. Затем мы посмотрим, как это у неё получается, чтобы можно было подправить её в сторону улучшения.
В строке содержится два шага. Первый делает матричное перемножение l0 и syn0. Второй передаёт вывод через сигмоиду. Размерности у них следующие:
(4 x 3) dot (3 x 1) = (4 x 1)
Матричные умножения требуют, чтобы в середине уравнения размерности совпадали. Итоговая матрица имеет количество строк, как у первой, а столбцов – как у второй.