Цель работы: показать возможности языка программирования Visual Basic в работе с символьными величинами.
Скачать:
 volkova_sasha_igra_slov_2.zip |
1.58 МБ |
Предварительный просмотр:
Моя работа – ИГРА «Создание слов».
Ученица 9А класса Волкова Александра
Руководитель: Коноплева Мария Петровна
Сразу скажу, что подобной программы мы не видели ни в одном пособии или сайте интернета, то есть всю программу от начала до конца мы придумали и запрограммировали сами.
По программе обучения предмету «ИНФОРМАТИКА» нами, учениками 8-го класса, была пройдена тема «Символьные величины и символьные функции». Проще говоря, это — программирование слов, фраз и целых предложений и различные их преобразования.
Создание реальной программы на Visual Basic .NET 1/9
Когда на дом было задано упражнение: создать максимально возможное количество слов из одного исходного слова, родилась идея создать при помощи знакомых учащимся символьных функций программу, которая автоматически выдавала бы на экран придуманные слова и производила их подсчет.
Цель работы : показать возможности языка программирования Visual Basic в работе с символьными величинами.
Для реализации поставленной задачи был использован язык программирования Visual Basic. Название Visual Basic говорит само за себя. Уже по слову «Visual» можно догадаться, что в Visual Basic реализован визуальный стиль программирования. Мы даже не программируем, а проектируем приложение. Наша первая задача при этом — создать рабочую среду, прежде чем начать набирать первую строку кода.
Сразу покажу работу созданной программы.
Сыграем! (С помощью гиперссылки переходим к файлу игровой программы).
Вводим в текстовое поле любое слово (длина ограничена 10 символами) и нажимаем кнопку ВПЕРЕД. Буквы распределяются по отдельности в текстовые поля.
Для создания слов щелкаем мышью по командным кнопкам, соответствующим буквам. После набора слова целиком нажимаем кнопку ГОТОВО для фиксации слова в строке на форме и подсчета количества слов.
Помогите мне придумать слова! (Обращаешься к публике, набираешь по их просьбе слова). Ну как, программа работает? Да! Вернемся к презентации.
Для реализации поставленной задачи был использован язык программирования Visual Basic. Название Visual Basic говорит само за себя. Уже по слову «Visual» можно догадаться, что в Visual Basic реализован визуальный стиль программирования. Мы даже не программируем, а проектируем приложение. Наша первая задача при этом — создать рабочую среду, прежде чем начать набирать первую строку кода.
Проект без «украшений» выглядит так.
Создание программного кода
а – символьная переменная для ввода любого слова, длину которого ограничиваем 10 символами;
Программирование макросов на VBA в Excel
b(10) – символьный массив, значения которого – буквы введенного слова по порядку;
i – счетчик цикла;
L – числовая переменная для подсчета длины введенного слова;
k – числовая переменная для подсчета количества придуманных слов.
Распределяем буквы в соответствующие текстовые поля.
Распечатаем придуманные слова на ФОРМУ.
Подсчитаем количество придуманных слов.
Оформим проект как самостоятельную программу:
Файл — Make Projekt exe
Источник: nsportal.ru
Министерство образования и науки Российской Федерации
Основы проектирования консольных приложений на языке Visual Basic
Методические указания для выполнения лабораторных работ по курсу «Информатика» студентами всех специальностей и направлений
Основы проектирования консольных приложений на языке Visual Basic
Методические указания для выполнения лабораторных работ по курсу «Информатика» студентами всех специальностей и направлений
Нижний Новгород: ННГАСУ, 2011
В методических указаниях представлены задания и пояснения к выполнению лабораторных работ в среде разработки Microsoft Visual Studio 2010 на языке Visual Basic в рамках курса «Информатика».
Составители: канд. техн. наук доцент Д. И. Кислицын,
канд. физ.-мат. наук доцент Т. М. Вежелис, старший преподаватель Ю.А. Громов
Под редакцией д-ра физ.-мат. наук, профессора А. Н. Супруна
Требования к выполнению работ
При подготовке к лабораторной работе студент должен изучить соответствующие разделы лекционного курса. В ходе выполнения лабораторной работы студент должен подготовить письменный отчет, включающий:
- номер, тему и цель лабораторной работы;
- номер варианта и перечень заданий;
- входные и выходные данные для каждого задания;
- блок-схему программы;
- текст программы;
- результаты вычислений (при необходимости дополнить соответствующими таблицами);
- общие выводы по результатам лабораторной работы.
Лабораторная работа №1
Тема: Создание простейшего консольного приложения в среде Visual Basic 2010. Цель работы: Знакомство со средой Visual Basic 2010. Создание консольного приложения. Написание арифметических выражений. Изучение разных способов ввода данных.
Задания
- Составить блок–схему линейного алгоритма вычисления заданного арифметического выражения (варианты заданий лабораторной работы №1 приведены в таблице 1.1).
- Создать пустой проект консольного приложения ConsoleApplication.
- Составить программу вычисления заданного выражения на языке Visual Basic.
- Запустить программу.
- Изменить программу так, чтобы исходные данные вводились с клавиатуры.
Порядок выполнения работы
1. Составление блок – схемы вычисления арифметического выражения. В качестве примера рассмотрим следующее выражение: Z=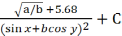
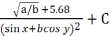
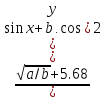, где a=114.6; b=53.47 . 10 3 ; x=36 o ;y=0.87
- Входные данные: a=114.6; b=53.47 . 10 3 ; x=36 o ; y=0.87. Выходные данные:Z.
Для удобства вычислений введем вспомогательные переменные: x1 — радианная мера аргумента х, заданного в градусах, z1 — числитель дроби, z2 — знаменатель дроби.
- Нарисуйте блок – схему с соответствующими пояснениями (рис. 1.1).
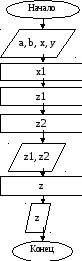Пояснения Ввод a,b,x,y Перевод x из градусов в радианы x1=π*x/180 Вычисление z1=
Вычисление z2= (sinx+b.cosy)2 Вывод z1,z2 Вычисление z=z1/z2
Вывод значения z Рис.1.1. Блок-схема алгоритма 2. Создание пустого проекта консольного приложения ConsoleApplication. 2.1. Запустить среду разработки MS Visual Studio 2010, указав в качестве параметров разработки используемый язык программирования – Visual Basic (рис.1.2). 
Рис.1.2. Выбор языка программирования 2.2. Создать новый проект консольного приложения (ConsoleApplication), используя следующие пункты меню: Файл – Создать проект –VisualBasic- Консольное приложение. В поле Имя задать имя проекта, например, свою фамилию, и нажать кнопку Ok (рис.1.3).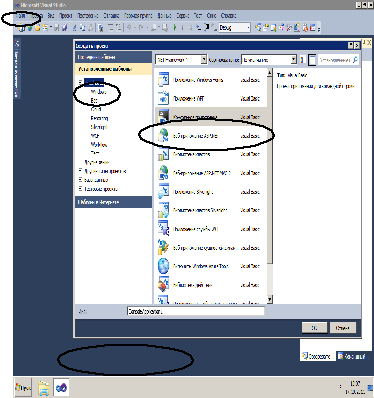 
Рис.1.3. Создание нового проекта 3.Составление программы вычисления заданного выражения на языке Visual Basic. 3.1. После создания нового проекта консольного приложения появляется следующее диалоговое окно, содержащее заготовку текста головного модуля проектируемой программы (рис.1.4). 
Рис.1.5. Сборка программы 4. Запуск программы выполняется пунктами меню: Отладка – Начать отладку (рис.1.6). 
Рис.1.6. Запуск программы После получения результата на экране выписать полученное значение в отчёт выполнения работы и нажать клавишу Enter для завершения работы программы. Сохранить проект, используя пункт меню: Файл — Сохранить все (рис.1.7). А затем в появившемся окне указать путь сохранения проекта: Мои документы Номер группы Фамилия (рис.1.8). 
Рис.1.7. Сохранение проекта 
Рис.1.8. Указание пути сохранения проекта 5. Изменение способа ввода исходных данных (ввод с клавиатуры). Для ввода данных с клавиатуры используйте функцию Console.ReadLine(). Пример использования: A = Val(Console.ReadLine()). Здесь переменной A присваивается значение, введённое с клавиатуры. Функция Val() преобразует введённое с клавиатуры значение из текстового типа в числовой. 5.1. Самостоятельно измените текст программы так, чтобы все исходные данные вводились с клавиатуры. 5.2. Выполните сборку и запуск программы, введите исходные данные и сравните полученный результат с результатом, полученным в п.4. Таблица 1.1. Варианты заданий к лабораторной работе № 1.
| № задания | Выражение | Значения переменных |
| 1 |  |
a=3.17b=5.34x=4.1 |
| 2 |  |
a=8.31b=4.50x=2.71 |
| 3 |  |
a=8.31b=4.50x=4.412 |
| 4 |  |
a=5.34b=4.10 |
| 5 |  |
a=2.412 |
| 6 |  |
a=2.412x=29 |
| 7 |  |
a=2.71b=5.34x=33 |
| 8 |  |
a=7.31b=2.17x=21 |
| 9 |  |
a=3.115x=51 |
| 10 |  |
a=4.115x=44 |
| 11 |  |
a=8.133 |
| 12 |  |
a=8.71x=78 |
| 13 |  |
a=8.735b=2.41 |
| 14 |  |
a=3.891x=64 |
| 15 |  |
a=8.735x=22 |
| 16 |  |
a=12.13x=14 |
| 17 |  |
u=2.95104y=0.88x=1.22103 |
| 18 |  |
a=6.35b=1.5102x=0.56 |
| 19 |  |
l=2.7103m=6.54x=0.82 |
| 20 |  |
a=3.42b=152102x=14.5 |
| 21 |  |
a=4.78b=2.83102x=35.5 |
| 22 |  |
l=2.8104n=1.45x=2.2y=8.2 |
| 23 |  |
p=3.7103q=-21.2b=2.17x=132 |
| 24 |  |
a=-1.5102b=0.98x=15.2 |
| 25 |  |
u=2.72v=1.045103x=0.24 |
| 26 |  |
m=5.48n=0.75102q=2.8 |
| 27 |  |
p=2.8102q=0.35m=37.2 |
| 28 |  |
U=2.75102V=1.54 |
| 29 |  |
p=5.75q=1.3 |
| 30 |  |
p=1.3103x=4.75y=23.2 |
Источник: studfile.net
Программа выполненная на языке Microsoft Visual Basic 6.0
Вычислительная машина, счётная машина — механизм, электромеханическое или электронное устройство, предназначенное для автоматического выполнения математических операций.
В последнее время, это понятие чаще всего ассоциируется с различными видами компьютерных систем. Тем не менее, вычислительные механизмы появились задолго до того, как заработал первый компьютер.
Ещё в 1623 году немец Вильгельм Шиккард (нем. Wilhelm Schickard) создал так называемые «Считающие часы», которые сегодня принято считать первым автоматическим калькулятором. В письмах к Иоганну Кеплеру Шикард объяснял, как можно использовать его машину для расчёта астрономических таблиц. Машина Шикарда умела складывать и вычитать шестизначные числа, оповещая звонком о переполнении.
Более сложные вычисления выполнялись с помощью набора костяшек Непера, установленного на корпусе механизма. Оригинал машины был потерян при пожаре ещё до начала двадцатого столетия. В 1960 году на основе сохранившихся чертежей была построена копия этого вычислителя, подтвердившая его существование и работоспособность.
В 1642 году машину, помогающую в сложении чисел, изобрёл французский учёный Блез Паскаль. «Паскалина», как назвал свою конструкцию изобретатель, представляла собой механическое устройство в виде ящичка, наполненного многочисленными шестерёнками. Складываемые числа вводились в машину за счёт соответствующего поворота наборных колёсиков. На каждом из этих колёсиков, соответствовавших одному десятичному разряду, были нанесены деления с цифрами от 0 до 9. При вводе числа колёсики прокручивались до соответствующей цифры.
Теоретическая часть
Основными компонентами компьютера являются процессор, память, устройства ввода и вывода. С помощью устройства ввода программа и исходные данные попадают в память. Программа содержит последовательность инструкций, которую выполняет процессор. Результаты выполнения программы поступают в устройства вывода. В качестве устройства ввода, как правило, используется клавиатура, в качестве устройства вывода — дисплей, на котором высвечиваются результаты выполнения программ, или принтер.
Наряду с клавиатурой, дисплеем и принтером используются дисководы и накопители на жестких дисках — устройства, осуществляющие запись и чтение информации. Это означает, что результаты, полученные на некотором этапе выполнения программы и записанные на магнитный диск, могут быть использованы на последующих этапах выполнения программы как исходные данные.
Рис.2. Структурная схема ПЭВМ
На рис.2 изображена структурная схема ПЭВМ, которая содержит следующие основные компоненты:
1) ЦП — центральный процессор, который управляет работой ПЭВМ а и выполняет все вычисления;
2) ОЗУ — оперативное запоминающее устройство, в котором располагаются программы, выполняемые ПЭВМ, используемые программами данные.
3) ПЗУ — постоянное запоминающее устройство, в котором располагаются программы, выполняемые ПЭВМ при своём включении.
Схема содержит следующие компоненты, которые предназначены для связи ПЭВМ с внешними устройствами:
1) Контроллер дисплея — позволяет подключить процессор к видео контрольному устройству, обеспечивает передачу видеоинформации и переключение видеорежимов дисплея;
2) Контроллер клавиатуры — позволяет подключить процессор к устройству ручного ввода информации, обеспечивает опрос каждой клавиши и передаёт процессору код нажатой клавиши;
3) Порты ввода — вывода, через которые процессор обменивается данными с внешними устройствами, предназначены для подключения к ним внешних устройств, таких как принтер, динамик, внешние устройства памяти;
4) Контроллер накопителя на диске — связывает накопители внешней оперативной памяти с ОЗУ, обеспечивает приём, передачу информации от носителя;
На схеме показаны следующие внешние устройства ПЭВМ:
1) Дисплей — основное средство оперативного вывода информации, предназначен для вывода текстовой или графической информации на экран.
2) Клавиатура — стандартное устройство ввода информации, основное средство взаимодействия пользователя с ПЭВМ.
3) Принтер — устройство печати текстовой и графической информации.
Принтеры бывают 3х типов — матричные, струйные и лазерные.
4) Накопитель на гибких магнитных дисках — устройство внешней памяти — служит для долговременного хранения информации — программ, архивных данных и т.д. Ёмкость носителя и скорость передачи данных незначительная.
5) Накопитель на жёстких магнитных дисках — устройство внешней памяти — служит для долговременного хранения информации — программ, архивных данных и т.д. Ёмкость носителя и скорость передачи данных высокая.
Задача 1.
Выполнить расчет максимальной мощности двигателя автомобиля и расчет внешней характеристики двигателя при следующих начальных условиях:
| mo, кг | Vmax, км/ч | Kв кг/м 3 | F, м 2 | Ψv | nN мин -1 | Kv | ηтр |
| 7000 | 0,62 | 3,9 | 0,021 | 1,2 | 0,88 |
Максимальная мощность двигателя тягача по условию обеспечения заданной максимальной скорости рассчитывается по формуле:
, (1)
где Nemax- искомая максимальная мощность, кВт;
Nv – мощность на режиме максимальной скорости, кВт;
Kv – отношение частоты вращения коленчатого вала двигателя при максимальной скорости движения тягача к номинальной частоте вращения:
, (2)
nN- частота вращения коленчатого вала двигателя на режиме максимальной мощности (номинальная), мин -1
nv- частота вращения коленчатого вала двигателя при максимальной скорости автомобиля, мин -1 .
Мощность на режиме максимальной скорости определяется по формуле (3):
, (3)
где m0 — масса тягача, кг;
Ψv — суммарный коэффициент сопротивления дороги;
V max – заданная максимальная скорость тягача;
ηтр – КПД трансмиссии;
Kв — коэффициент сопротивления воздуха, кг/м 3 ;
F – лобовая площадь тягача, м 2 .
Внешняя характеристика двигателя представляет собой зависимость мощности, крутящего момента от частоты вращения коленчатого вала двигателя при полном открытии заслонки карбюратора.
При известном значении максимальной мощности Nemax мощность в любой другой точке характеристики может быть найдена по формуле Лейдермана:
(4)
где Ne -мощность двигателя при произвольном значении частоты вращения коленчатого вала, кВт;
Nemax -максимальная мощность двигателя, кВт;
n — заданная частота вращения коленчатого вала, мин -1 ;
nN -частота вращения коленчатого вала на режиме максимальной мощности, мин -1 ;
a,b,c -коэффициенты, принимаемые для бензиновых двигателей, равны 1.
Крутящий момент в любой точке характеристики определяется по формуле:
Me=9549 (Ne/ n), (5)
Составим схему алгоритма. В алгоритме будет три блока: ввод исходных данных, расчет по формулам(1)-(5) и вывод результата.
По приведенной блок-схеме была составлена программа, листинг которой приведен ниже.
program lab1;
var m0,vmax,Ke,F,Fv,nN,Ky,n_tr:real;
writeln (‘Vvedite ishodnye dannye:’);
write (‘m0=’);readln(m0);
write (‘Vmax=’);readln(Vmax);
write (‘Ke=’);readln(Ke);
write (‘F=’);readln(F);
write (‘Fv=’);readln(Fv);
write (‘nN=’);readln(nN);
write (‘Ky=’);readln(Ky);
write (‘n_tr=’);readln(n_tr);
Nv:=2.725E-03*m0*Fv*Vmax/n_tr+2.14e-05*Ke*F*sqr(Vmax)*Vmax/n_tr;
Ne:=Ne_max*(n_v/nN+sqr(n_v/nN)-sqr(n_v/nN)*n_v/nN);
writeln(‘Ne_max=’,Ne_max);
writeln(‘n_v=’,n_v);
Решение этой же задачи было проведено в ЭТ Excel. Ниже представлен лист с решением и результатами.
Программу написанную на языке Паскаль копирую и вставляю в проект, затем исправляю существенные различия.
Задача 2.
Вычислить функцию 
, для 
с шагом 
.
| № | a | b | h | f(x) |
| Начало отрезка | Конец отрезка | Шаг по отрезку | ||
| -7000 |  |
Выполним схему алгоритма.
Эта схема была реализована на языке Паскаль в трех вариантах: были задействованы циклы с предусловием, с постусловием и с параметром. Листинги программ приведены ниже.
а) Цикл с постусловием
program lab21;
б) Цикл с предусловием
program lab22;
в) Цикл с параметром
program lab23;
x,y,a,b,h,n1: real;
n ,i : integer;
for i:=0 to n do
Задача 3
Применить метод деления отрезка пополам на интервале 
и найти с точностью 
корни уравнения 
.
| № |  |
 |
 |
| -7000 |  |
Алгоритм метода половинного деления заключается в следующем:
1. Выбрать нулевое приближение x0=(a+b)/2.
2. Если f(x0)=0, то x0 очевидно является корнем уравнения.
3. Если f(x0)≠0, то проверить условия f(x0)×f(a) и f(x0)×f(b) и выбрать тот из отрезков [a, х0], [х0, b], на границах которого выполнено одно из этих условий (т.е. функция f(х) имеет на концах отрезка противоположные знаки).
4. Выбранный отрезок вновь разделить пополам и вычислить значение x1.
5. Для х1 проверить условие f(х1)=0 и, если оно не выполняется, вернуться к п. 4.
6. Процесс деления отрезков пополам продолжить до тех пор, пока длина отрезка, на концах которого функция имеет противоположные знаки, не будет меньше e .
7. Принять, что условие f(xk)= 0 выполнено, если
Ниже приведены блок-схема алгоритма и листинг программы на языке Паскаль.
Program lab3;
function f1 (x: real): real;
iteraz: integer;
write (‘Input a = ‘); readln (a);
write (‘Input b = ‘); readln (b);
write (‘Input e = ‘); readln (e);
while (f1(x)<>0) and (abs(a-b)>e) do
iteraz:=iteraz+1;
writeln (‘n=’, iteraz,’ x=’, x:3:6,’ f(x)=’, f1(x):3:6);
Решение этой задаче было проведено и в MS Excel. Лист с решением задачи и ответом приведен ниже.
Задача 4.
Вычислить определенный интеграл методом прямоугольников: или трапеций, на выбор.
, 
, 
, 
, с точностью 
.
Формула метода прямоугольников:
Формула метода трапеций: .
| № |  |
 |
 |
| -9000π |  |
Алгоритм метода трапеций заключается в следующем:
1. Отрезок [a,b] разбивается на n равных частей.
2. Интеграл представляет собой площадь криволинейной трапеции, ограниченной осью OX, прямыми x=a и x=b и графиком функции. Очевидно, что интеграл от функции на отрезке равен сумме интегралов от этой же функции на каждом из маленьких отрезков, полученных в результате разбиения. Но на каждом из маленьких отрезков мы приближенно заменяем площадь криволинейной трапеции на площадь прямолинейной трапеции с основанием (высотой), равным длине маленького отрезка, и высотами (основаниями) f(xn) и f(xn+1), где xn – левая граница отрезка, xn+1 – правая граница отрезка. Основание (высота трапеции) равно
(b-a)/n, и таким образом площадь трапеции равна
(f(xn)+f(xn+1))(b-a)/2n. У нас всего n трапеций, причем каждые две соседние трапеции имеют одинаковые высоты (основания). Таким образом, в сумму каждое из f(xn) кроме f(a) и f(b) войдет дважды, и таким образом весь интеграл вычисляется как , где .
3. В методе трапеций не определен шаг (количество отрезков разбиения). Очевидно, что чем больше количество отрезков, тем более точным будет результат. Поэтому, задаем начальное значение n (например n=10) и вычисляем интеграл.
4. После этого удваиваем n и снова вычисляем интеграл (п. 2). Сравнивая полученные результаты, делаем вывод, достигнута ли требуемая точность.
5. Если результаты отличаются друг от друга меньше чем на ε, то требуемая точность достигнута. Если нет, то снова удваиваем n и вычисляем интеграл еще раз (возвращаемся к п. 4).
Ниже представлена блок-схема алгоритма и листинг программы.
program pr4;
h,a,b,S,dS,P,x,eps:real;
function f(x:real) : real;
f:=0,1*sin(0.1*x+0.0025*x*x)/cos(0.1*x+0.0025*x*x);
Источник: megaobuchalka.ru