Ai-бот эксперт в любой области и идеальный собеседник для получения надежных и полезных ответов и советов на различные темы, включая науку, историю, технологии, искусство, спорт, здоровье, культуру и многое другое.
Еще советы
- д досуг и развлеченияКакой подарок на 8 марта ребенок может сделать своими руками.
- с стиль и красотаКак предотвратить выпадение волос.
- с семья и домКогда начинается токсикоз при беременности.
- к компьютеры и интернетГде можно найти песни из реклам.
- о образованиеФразеологизмы: смысл, примеры, функции в речи.
- к компьютеры и интернетКак настроить почту: подробное руководство для новичков.
- с стиль и красотаНатуральный жемчуг: как его отличить от подделки.
- с стиль и красотаКак определить размер кольца.
- к компьютеры и интернетКак активировать Касперского 2011: пошаговая инструкция.
- о образованиеСкрипт: от простых команд до сложных программ.
Ответы на вопросы: Информатика
- И ИнформатикаКаковы положительные и отрицательные стороны работы с папками общего доступа.
- И Информатика1. составьте программу, увеличивающую введенное число на 1, если оно больше или равно100 и уменьшающее число на 1 в противном случае. 2. составить программу, запрашивающую возраст.
- И ИнформатикаУмоляю надо построить таблицу истинности .
- И ИнформатикаСреди двузначных чисел найти те,которые кратны 13. как это сделать в паскале ? .
- И ИнформатикаДана последовательность операторов: a:=1; b:=1; repeat a:=a+1; b:=b*2; until b 8 s:=a+b Сколько раз будет повторен цикл и какими будут значения переменных a,b,s, после исполнения.
- И ИнформатикаУ исполнителя Альфа две команды: 1) Прибавь 2 2) Умножить на b Выполняя первую из них, Альфа увеличивает число на экране на 2, а выполняя другую, умножает это число на b. Программа.
- И ИнформатикаТреугольник задан координата вершин А(0; 0), В(i; i-1) и С(-i; i+1), где i — 11. 1. Вычислить высоту ha и биссектрису Wc. 2. Вычислить медиану mа и биссектрису Wb.
- И ИнформатикаСтатья, набранная на компьютере, содержит 16 страниц, на каждой странице 32 строки, в каждой строке 30 символов. определите информационный объём статьи в кодировке кои-8, в которой.
- И Информатика4«условный оператор» написать программу: дано четырехзначное число. определить, входит ли в него цифра 6.
- И Информатика1) (p+k*4)/(4*t)-4*p*k/(3-2*b) 2)(x1**3-y1**3)-(x**3-2)3) abs(4*x)+(3-3x)/5*y4)abs(3-x)+x**3/y**2.
Полный доступ
Обеспечит эффективное и быстрое обучение, предоставляя неограниченный доступ к базе знаний и получению ответов от экспертов и AI-советника.
7.8 Рекурсия в Python. Рекурсивная функция Часть 1
Источник: znay-otvet.com
СИРИУС ЗАДАНИЕ ХЕЛП Не запуская код, ответьте на вопрос: что выведет на экран данная программа? def f(a): global a global b b, c = a, b def g(): global a global d c = ‘0’ a = d + c a=’2′ b=’3′ c=’5′ d=’7′ f() g()f() print(a+b+c+d)
Запускаем функцию f(), глобально меняется переменная b на 2.
41 Рекурсия в Python. Рекурсивная функция Часть 1
Запускаем функцию g(), глобально меняется переменная a на 70.
Запускаем функцию f(), глобально меняется переменная b на 70.
Программа выведет: 707057
Ответ разместил: Гость
var a: array [1..10] of integer;
for i : = 1 to 10 do
for i: = 1 to 10 do
if a[min]> a[i] then min: =i;
Ответ разместил: Гость
program z2_65; uses crt; label a1,a2,a3,a4,a5,a6,a7; var a,s,h,rv,ro,p: real; n: integer; beginclrscr; writeln(‘укажите номер пункта: ‘); writeln(‘1. дана сторона треугольника.’); writeln(‘2. дана площадь треугольника.’); writeln(‘3. дана высота треугольника.’); writeln(‘4. дан радиус вписанной окружности треугольника.’); writeln(‘5. дан радиус описанной окружности треугольника.’); read(n); case n of1: begin write(‘a=’); read(a); goto a1; end; 2: begin write(‘s=’); read(s); goto a2; end; 3: begin write(‘h=’); read(h); goto a3; end; 4: begin write(‘r=’); read(rv); goto a4; end; 5: begin write(‘r=’); read(ro); goto a5; end; elsebeginwrite(‘такого номера пункта нет.’); goto a7; end; end; a1: rv: =a/2; ro: =a/sqrt(3); s: =sqrt(3)*sqr(a)/4; h: =2*s/a; goto a6; a2: a: =sqrt(4*s/sqrt(3)); h: =2*s/a; rv: =a/2; ro: =a/sqrt(3); goto a6; a3: a: =2*h/sqrt(3); s: =a*h/2; rv: =a/2; ro: =a/sqrt(3); goto a6; a4: a: =2*rv; ro: =a/sqrt(3); s: =sqrt(3)*sqr(a)/4; h: =2*s/a; goto a6; a5: a: =sqrt(3)*ro; s: =(a*a*a)/(4*ro); h: =2*s/a; rv: =a/2; a6: writeln(‘a=’,a: 2: 2); writeln(‘s=’,s: 2: 2); writeln(‘h=’,h: 2: 2); writeln(‘r=’,ro: 2: 2); writeln(‘r=’,rv: 2: 2); a7: readkey; end.
Источник: vse-znaniya.com
Кратко о рекурсии. Задачи на рекурсию

Рекурсия — известное и распространённое явление, которое встречается как в математике, так и в повседневной жизни. Рекурсивным называют объект, который частично состоит или определяется с помощью самого же себя. Например, если вы включите веб-камеру и наведёте её на экран компьютера, она будет записывать экран компьютера, выводя изображение на тот же самый экран компьютера. То есть мы увидим что-то наподобие замкнутого цикла.
Пример бесконечной рекурсии в литературе — докучные сказки типа «У попа была собака», где конец подменяется началом и всё продолжается снова и снова. А вот ещё примеры рекурсии:

О рекурсии в программировании
Что касается программирования, то здесь рекурсия связана с функциями, то есть понятие рекурсивной функции известно любому программисту. В данном случае рекурсия — это определение части метода или функции через саму себя. Можно сказать, что это функция, вызывающая саму себя в своём теле (непосредственно) либо через другую функцию (косвенно).
Впрочем, о рекурсии сказано много, поэтому вы без труда найдёте нужную информацию на просторах сети. Мы же поговорим о рекурсии с точки зрения решения задач. Именно задачи и их решение являются наиболее эффективным средством для понимания рекурсии, как таковой.
Как решают задачи на на рекурсию?
Во-первых, нужно уяснить, что рекурсия — это, по сути, перебор. Да и вообще, то, что можно решить итеративно, можно решить и рекурсивно, используя рекурсивную функцию. То есть практически любой алгоритм, который реализован в рекурсивной форме, можно переписать в итерационной форме и наоборот. Вопрос лишь в том, зачем это нужно и насколько эффективно.
Идём дальше. Так же, как и у цикла (перебора), рекурсия должна иметь условие остановки, называемое базовым случаем. Иначе и цикл, и рекурсия будут работать бесконечно. Условие остановки определяет шаг рекурсии.
Рекурсивная функция вызывается, пока не произойдёт остановка рекурсии (не сработает базовое условие и не произойдёт возврат к последнему вызову функции). Именно поэтому решение задачи на рекурсию сводится к решению базового случая.
Если мы решаем сложную задачу (небазового случая), мы выполняем несколько рекурсивных вызовов либо шагов, т. к. наша цель — упростить задачу. И делать это до тех пор, пока не придём к базовому решению.
Ещё раз. Рекурсивная функция включает в себя: — базовый случай, он же условие остановки; — шаг рекурсии, он же условие продолжения.
Давайте рассмотрим это, изучив пример нахождения факториала:
public class Solution < public static int recursion(int n) < // условие выхода // Базовый случай // когда остановиться/повторять рекурсию ? if (n == 1) < return 1; >// Шаг рекурсии/рекурсивное условие return recursion(n — 1) * n; > public static void main(String[] args) < System.out.println(recursion(5)); // вызов рекурсивной функции >>
Здесь базовое условие — когда n=1. Раз мы знаем что 1!=1, для вычисления 1! нам ничего не надо.
И чтобы определить 2! Можно использовать 1!, то есть 2!=1!2. А чтобы вычислить 3! потребуется 2!3… Для вычисления n! нужно (n-1)!*n. Вот это и есть шаг рекурсии. Другими словами, чтоб нам получить значение факториала от числа n, нам достаточно умножить на n значение факториала от предыдущего числа.
Давайте рассмотрим ещё парочку задач о рекурсии разного уровня сложности. Не спешите сразу смотреть решение, а попробуйте выполнить расчёты самостоятельно.
Задача о рекурсии № 1: От 1 до n
У вас есть натуральное число n. Необходимо вывести все числа от 1 до n.
public class Solution < public static String recursion(int n) < // Базовый случай if (n == 1) < return «1»; >// Шаг рекурсии/рекурсивное условие return recursion(n — 1) + » » + n; > public static void main(String[] args) < System.out.println(recursion(10)); // вызов рекурсивной функции >>
Задача о рекурсии № 2. От А до В
Имеются 2 целых числа A и В (каждое из них в отдельной строке). Необходимо вывести все числа от A до B включительно. Если A < B, числа выводятся по возрастанию, в обратном случае — по убыванию.
public class Solution < public static String recursion(int a, int b) < // основное условие задачи if (a >b) < // Базовый случай if (a == b) < return Integer.toString(a); >// Шаг рекурсии/рекурсивное условие return a + » » + recursion(a — 1, b); > else < // Базовый случай if (a == b) < return Integer.toString(a); >// Шаг рекурсии/рекурсивное условие return a + » » + recursion(a + 1, b); > > public static void main(String[] args) < System.out.println(recursion(20, 15)); // вызов рекурсивной функции System.out.println(recursion(10, 15)); // вызов рекурсивной функции >>
Задача о рекурсии № 3. Функция Аккермана
Функция Аккермана A(m,n), играет важную роль в теории вычислимости. Она определена следующим образом:
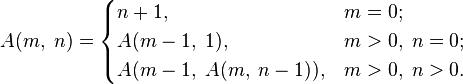
Условие задачи: есть 2 целых неотрицательных числа m и n, каждое из них находится в отдельной строке. Необходимо вывести A(m,n).
public class Solution < public static int recursion(int m, int n) < // Базовый случай if (m == 0) < return n + 1; >// Шаг рекурсии/рекурсивное условие else if (n == 0 m > 0) < return recursion(m — 1, 1); >// Шаг рекурсии/рекурсивное условие else < return recursion(m — 1, recursion(m, n — 1)); >> public static void main(String[] args) < System.out.println(recursion(3, 2)); // вызов рекурсивной функции >>
Источник: otus.ru