На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др., то есть в тех случаях, когда нужно осуществить поиск и определить оптимальное значение какого-либо параметра или количество. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.
Обычно нами строится выражение этих значений в рамках некоторого интервала x , который может в свою очередь соответствовать всей области определения функции или ее части. Это может быть как отрезок [ a ; b ] , так и открытый интервал ( a ; b ) , ( a ; b ] , [ a ; b ) , бесконечный интервал ( a ; b ) , ( a ; b ] , [ a ; b ) либо бесконечный промежуток — ∞ ; a , ( — ∞ ; a ] , [ a ; + ∞ ) , ( — ∞ ; + ∞ ) .
В этом материале мы расскажем, как найти наибольшее и наименьшее значение явно заданной функции с одной переменной y=f(x) y = f ( x ), чтобы вам не нужно было искать это самостоятельно онлайн .
Наибольшее и наименьшее значение функции. 10 класс.
Основные определения
Начнем, как всегда, с формулировки основных определений: какое значение называют максимальным и минимальным?.
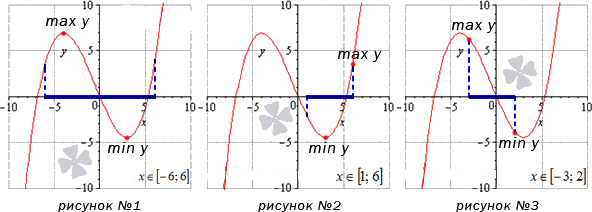
Как найти наибольшее и наименьшее значение непрерывной функции на открытом или бесконечном интервале
Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнавать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.
- Для начала нужно проверить, будет ли заданный интервал являться подмножеством области определения данной функции.
- Определим все точки, которые содержатся в нужном интервале и в которых не существует первой производной. Обычно они бывают у функций, где аргумент заключен в знаке модуля, и у степенных функций с дробно рациональным показателем. Если же эти точки отсутствуют, то можно переходить к следующему шагу.
- Теперь определим, какие стационарные точки попадут в заданный промежуток. Сначала приравняем производную к 0 , решим уравнение и подберем подходящие корни. Если у нас нет ни одной стационарной точки или они не попадают в заданный интервал, то сразу переходим к дальнейшим действиям. Их определяет вид интервала.
- Если интервал имеет вид [ a ; b ) , то нам надо вычислить значение функции в точке x = a и односторонний предел lim x → b — 0 f ( x ) .
- Если интервал имеет вид ( a ; b ] , то нам надо вычислить значение функции в точке x = b и односторонний предел lim x → a + 0 f ( x ) .
- Если интервал имеет вид ( a ; b ) , то нам надо вычислить односторонние пределы lim x → b — 0 f ( x ) , lim x → a + 0 f ( x ) .
- Если интервал имеет вид [ a ; + ∞ ) , то надо вычислить значение в точке x = a и предел на плюс бесконечности lim x → + ∞ f ( x ) .
- Если интервал выглядит как ( — ∞ ; b ] , вычисляем значение в точке x = b и предел на минус бесконечности lim x → — ∞ f ( x ) .
- Если — ∞ ; b , то считаем односторонний предел lim x → b — 0 f ( x ) и предел на минус бесконечности lim x → — ∞ f ( x )
- Если же — ∞ ; + ∞ , то считаем пределы на минус и плюс бесконечности lim x → + ∞ f ( x ) , lim x → — ∞ f ( x ) .
- В конце нужно сделать вывод на основе полученных значений функции и пределов. Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4 — 8 в первой части материала.
Условие: дана функция y = 3 e 1 x 2 + x — 6 — 4 . Вычислите ее наибольшее и наименьшее значение в интервалах — ∞ ; — 4 , — ∞ ; — 3 , ( — 3 ; 1 ] , ( — 3 ; 2 ) , [ 1 ; 2 ) , 2 ; + ∞ , [ 4 ; + ∞ ) .
Математический анализ, 13 урок, Наибольшее и наименьшее значение функции на отрезке
Решение
Первым делом находим область определения функции. В знаменателе дроби стоит квадратный (квадратичный) трехчлен, который не должен обращаться в 0 :
x 2 + x — 6 = 0 D = 1 2 — 4 · 1 · ( — 6 ) = 25 x 1 = — 1 — 5 2 = — 3 x 2 = — 1 + 5 2 = 2 ⇒ D ( y ) : x ∈ ( — ∞ ; — 3 ) ∪ ( — 3 ; 2 ) ∪ ( 2 ; + ∞ )
Найти наименьшее значение функции
Онлайн калькулятор поможет найти наименьшее значения функции на отрезке. Вычислить точки наименьшего значения функции в заданном интервале.
Для примера рассмотрим нахождение f(x)=x(x-3)^2 минимального значения точки графика функции на отрезке от -2 до 5. Результат = -50.
Вам может понадобиться калькулятор для нахождения наибольшего значения функции.
Синтаксис
основных функций:
x a : x^a
|x| : abs(x)
√x : Sqrt[x]
n √x : x^(1/n)
a x : a^x
log a x : Log[a, x]
ln x : Log[x]
cos x : cos[x] или Cos[x]
sin x : sin[x] или Sin[x]
tg : tan[x] или Tan[x]
ctg : cot[x] или Cot[x]
sec x : sec[x] или Sec[x]
cosec x : csc[x] или Csc[x]
arccos x : ArcCos[x]
arcsin x : ArcSin[x]
arctg x : ArcTan[x]
arcctg x : ArcCot[x]
arcsec x : ArcSec[x]
arccosec x : ArcCsc[x]
ch x : cosh[x] или Cosh[x]
sh x : sinh[x] или Sinh[x]
th x : tanh[x] или Tanh[x]
cth x : coth[x] или Coth[x]
sech x : sech[x] или Sech[x]
cosech x : csch[x] или Csch[е]
areach x : ArcCosh[x]
areash x : ArcSinh[x]
areath x : ArcTanh[x]
areacth x : ArcCoth[x]
areasech x : ArcSech[x]
areacosech x : ArcCsch[x]
конъюнкция «И» ∧ :
дизъюнкция «ИЛИ» ∨ : ||
отрицание «НЕ» ¬ : !
импликация =>
число π pi : Pi
число e : E
бесконечность ∞ : Infinity, inf или oo
Пожалуйста напишите с чем связна такая низкая оценка:
Источник: allcalc.ru
Найти наименьшее значение функции программа
: 8
Найдите наибольшее и наименьшее значение функции
СРОЧНО Помогите плиз cоставить программульку на паскале:
Найдите наибольшее и наименьшее значение функции f(x)=3*x*x+x-4, если на заданном интервале [Xmin;Xmax] аргумент изменяется с шагом дельта x
: 2,740
Решается это примерно так:
uses crt; var x,xmin,xmax,dx,ymin,ymax:real; y:array[1..100]of real; i,n:integer; begin clrscr; write(‘xmin=’);readln(xmin); write(‘xmax=’);readln(xmax); write(‘dx=’);readln(dx); x:=xmin;n:=0; while xymax then begin ymax:=y[i]; end; end; writeln(‘ymin=’,ymin:6:2,’ ymax=’,ymax:6:2); readln end.
Форумчанин
: 302
puporev, прикольный алгоритм — сам придумал или скачал где-то?
Сори за флуд.
: 8
puporev, спасибо тебе огромное
| Похожие темы | ||||
| Тема | Автор | Раздел | Ответов | Последнее сообщение |
| программа считывающая пять целых чисел и определяющая, печатающая наибольшее и наименьшее число из них | Syber | Общие вопросы C/C++ | 3 | 30.06.2008 22:39 |
| Для вещественного массива А(20)вычислить наибольшее и наименьшее значения модуля раз-ти между сосед.эл-ми | faix | Помощь студентам | 2 | 14.11.2007 13:25 |
| Выбрать из таблицы наименьшее значение | John_chek | БД в Delphi | 2 | 14.05.2007 17:17 |
| Наибольшее и наименьшее значения функции | mcblack | Помощь студентам | 9 | 26.04.2007 10:53 |
| Вычислить приближенное значение функции Бесселя | IsapS | Паскаль, Turbo Pascal, PascalABC.NET | 5 | 17.01.2007 10:09 |
Источник: www.programmersforum.ru