

НАХОЖДЕНИЕ МАКСИМАЛЬНОГО И МИНИМАЛЬНОГО ЭЛЕМЕНТА В МАССИВЕ
Прусаков И.В. 1
1 гуманитарн-технический колледж Южно-Российского государственного политехнического университета (НПИ) имени М.И. Платова
Растеряев Н.В. 1
1 Южно-Российскогогосударственный политехнический университет (НПИ) имени М.И. Платова

Автор работы награжден дипломом победителя II степени
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
ВВЕДЕНИЕ
Основу современной инженерной деятельности составляет умение ставить задачи, разрабатывать алгоритмы и получать решения, производить анализ полученных данных и делать выводы. Поэтому в своей профессиональной деятельности инженер должен уметь грамотно применять персональный компьютер, современное программное обеспечение для решения научных и инженерных задач.
#1 паскаль, максимальный и минимальный элементы
Типичной задачей при обработке больших массивов данных является задача поиска максимума или минимума. Например, в списке успеваемости учеников класса найти самого прилежного. Иначе говоря, требуется выбрать наибольшее значение среднего балла и указать фамилию ученика. Или, в массиве среднесуточных температур окружающего воздуха за некоторый период наблюдений определить минимальное значение и указать дату самого холодного дня.
Цель работы: Разработка программы нахождения максимального и минимального элемента в среде программирования Паскаль-ABC.
Задачи:
1) Ознакомиться с алгоритмами поиска в массивах и методами их программной реализации.
2) Освоить приемы программирования в интегрированной среде Паскаль-ABC.
3) Разработать алгоритм и блок-схему нахождения максимального и минимального элемента в массиве.
4) Создать программу нахождения максимального и минимального элемента в массиве и протестировать её.
Объект исследования: алгоритмы поиска в массивах.
Предмет исследования: Паскаль-программа нахождения максимального и минимального элемента массива в среде Паскаль-ABC.
ОСНОВНАЯ ЧАСТЬ
1. Алгоритмы поиска информации
Очень часто в реальной жизни нам приходится сталкиваться с задачей поиска информации в объеме данных. Например, поиск фамилии ученика в журнале, поиск нужного слова в словаре. Существует множество алгоритмов поиска, но из всего многообразия алгоритмов рассмотрим два основных и наиболее часто используемых на практике.
В алгоритмах поиска существует два возможных окончания работы: поиск может оказаться удачным– заданный элемент найден в массиве и определено его месторасположение, либо проведенный поиск может оказаться неудачным– необходимого элемента в данном объеме информации нет.
Несмотря на то, что целью поиска является значение элемента, алгоритм поиска в случае удачного окончания выдает так же и местоположение искомого элемента, например его номер в массиве, так как по номеру элемента можно однозначно восстановить и его значение.
Урок 15. Паскаль с нуля. Максимальный элемент массива
Для оценки алгоритмов мы будем использовать такую характеристику, как сложность.
Пусть, например, человек ищет на полке книжку с определенным названием. Книги на полке стоят вразнобой, то есть не по алфавиту. Как будет действовать человек? Он будет сравнивать по порядку название каждой книги на полке с тем названием, которое ему нужно найти. В итоге он или найдет нужную ему книгу, или, просмотрев все книги на полке, не обнаружит нужной книги.
Этот пример передает суть алгоритма последовательного поиска в неупорядоченном массиве. Приведем его формальную запись.
Имеется одномерный массив a[1 … n], требуется найти элемент массива, равный P:
Алгоритм последовательного поиска в неупорядоченном массиве:
- Установить i = 1.
- Если ai = P, алгоритм завершил работу успешно.
- Увеличить i на 1.
- Если i ≤ n, то перейти к шагу 2. В противном случае алгоритм завершил работу безуспешно.
Оценим сложность алгоритма последовательного поиска. Естественно оценивать сложность по числу сравнений с искомым элементом. В худшем случае искомый элемент окажется на последнем месте или не будет найден, и тогда необходимо будет проделать n сравнений, то есть сложность алгоритма будет равна n. Такой поиск также называют линейным, так как он решает задачу поиска с линейной скоростью по количеству сравнений.
Усложним задачу. Пусть нам требуется найти минимальный элемент в неупорядоченном массиве. Оказывается, что и эта задача имеет линейную сложность, и для поиска минимального (максимального) элемента в неупорядоченном массиве требуется n – 1 сравнение. Запишем алгоритм поиска максимального элемента в текстовой (вербальной) форме.
Алгоритм поиска максимального элемента в неупорядоченном массиве:
- Установить счетчик равным 1 (i = 1).
- Положим значение текущего максимума равным первому исследуемому элементу (max = a1).
- Если исследованы еще не все элементы (i< n), то перейти к шагу 5, иначе алгоритм окончен (максимальный элемент равен max).
- Перейти к следующему элементу (увеличить i на единицу).
- Если рассматриваемый элемент больше, чем текущий максимум (ai >max), то значение ai присвоить max.
- Перейти к шагу 4.
Последовательный поиск не является самым эффективным алгоритмом поиска. Например, человеку нужно найти в русско-английском словаре перевод слова на английский язык. Если он будет искать его с помощью алгоритма последовательного поиска (просматривая все слова подряд), то он потратит очень много времени. На самом же деле интуитивно человек действует совсем по-другому.
Поиск слова в словаре наиболее приближен к алгоритму бинарного (двоичного) поиска, который также называют логарифмическим поиском, или методом деления пополам (дихотомией). Этот алгоритм достаточно эффективен, но использовать его можно только в случае, когда данные упорядочены. В этом алгоритме мы используем сравнение искомого элемента с серединным элементом и с помощью результата этого сравнения устанавливаем, в какой части данных находится искомый элемент.
Заметим, что даже если данные упорядочены, то использовать алгоритм бинарного поиска мы можем не всегда. Это касается тех случаев, когда мы не имеем доступа к любому элементу массива. Например, если данные поступают к нам последовательно.
2. Алгоритмы поиска максимального или минимального элемента массива
Алгоритмизация – это общая последовательность действий, которые необходимо выполнить для построения алгоритма решения задачи, в том числе – выделение конкретных шагов алгоритмического процесса, определение вида формальной записи для каждого шага и установление определённого порядка выполнения каждого шага.[1]
Пусть поставлена следующая задача: по известным данным среднесуточных температур и дат найти максимальную или минимальную температуру и соответствующую ей дату.
Принцип поиска максимального или минимального элемента массива заключается в следующем.Первое, что необходимо сделать – создать массивы данных и дат. При этом сначала вводится параметр n–число элементов создаваемых массивов. Для ввода элементов массива используется цикл с параметром. Вводятся числовое значение и дата в формате ДД.ММ.ГГ.
Для определения того, будем находить максимальный или минимальный элемент, целочисленной переменной flagбудем присваивать значения 1 или 0.
В дополнительную переменную заносится значение первого элемента массиваDan[ ], которое принимается за максимум (минимум); затем организовывается перебор оставшихся элементов массива, каждый из которых сравнивается с максимумом (минимумом); если текущий элемент массива оказывается больше (меньше), чем принятый за максимум (минимум), то этот элемент становится максимальным (минимальным). Таким образом, после завершения перебора элементов массива в дополнительной переменной окажется максимальное (минимальное) значение среди элементов массива.
Кроме этого введены еще две переменные imax и imin, которые будут использоваться для хранения номеров максимального и минимального элементов массива. После выхода из цикла будут найдены значения максимального или минимального элементов массива Dan[ ], а также их номера, по которым будут найдены соответствующие даты в массиве Tim[ ].
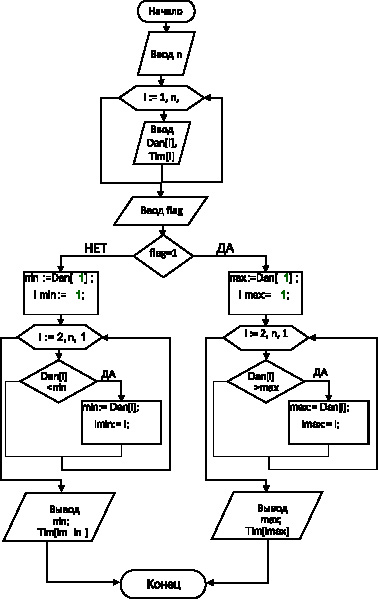
Представим разработанный выше алгоритм в виде блок-схемы.
Блок-схемой называется наглядное графическое изображение алгоритма, когда отдельные его этапы изображаются при помощи различных геометрических фигур − блоков, а связи между этапами (последовательность выполнения этапов) указываются при помощи стрелок. Типичные действия алгоритма изображаются геометрическими фигурами согласно ГОСТ 19.701-90.
Блок-схема алгоритма представлена на рисунке 1.
Рис. 1 − Блок-схема алгоритма нахождения максимального и минимального элемента
3.Интегрированная среда программирования Паскаль-ABC. Разработка и тестирование программы
На рис. 2 представлен скриншот разработанной программы в интегрированной среде программирования Паскаль-АВС
Рис. 2 − Скриншот программы
Система программирования Паскаль-ABC представляет собой диалект стандартного языка Паскаль. Система создавалась на факультете математики, механики и компьютерных наук ЮФУ как учебная среда программирования (автор − кандидат физико-математических наук, доцент кафедры алгебры и дискретной математики С. С. Михалкович).[2] По мнению разработчиков этой системы, первоначальное обучение программированию должно проходить в достаточно простых и дружественных средах, в то же время эти среды должны быть близки к стандартным и иметь богатые и современные библиотеки подпрограмм.
На рис. 3 представлен скриншот результатов нахождения максимального значения температуры и соответствующей ей дате.
Рис. 3 − Скриншот результатов нахождения максимального элемента
На рис. 4 представлен скриншот результатов нахождения минимального значения температуры в массиве и соответствующей ей дате.
Рис. 4 − Скриншот результатов нахождения минимального элемента массива
ЗАКЛЮЧЕНИЕ
В результате выполнения моей научно-исследовательской работы достигнута цель исследования – разработана программа нахождения максимального и минимального элемента в среде программирования Паскаль-ABC. Программа протестирована по двум ветвям вычислительного процесса: нахождение максимального и нахождение минимального элемента.
При этом я ознакомился с алгоритмами поиска информации в больших объемах данных. Освоил некоторые приемы программирования в интегрированной среде Паскаль-ABC. Разработал блок-схему и программу нахождения максимального и минимального элемента одномерного массива. Надеюсь, что полученные знания и навыки помогут мне успешно сдать экзамен по дисциплине информатика.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ И ЛИТЕРАТУРЫ
1. Логинов В.И.Основы алгоритмизации: учеб.-метод. пособие для студ. оч.заоч. обуч. технич. специальностей / В.И. Логинов, Л.Н. Шемагина. – Н. Новгород: Изд-во ФГОУ ВПО «ВГАВТ», 2010. – 81 с.
2. Михалкович С.С. Основы программирования: учеб.-метод. пособие для студ. 1 курса / В.И. Логинов, Л.Н. Шемагина. – Ростов-на-Дону: Изд-во ЮФУ, 2007. – 40 с.
Источник: school-science.ru
Поиск минимального и максимального элементов массива.
Одной из наиболее распространенных задач обработки массивов является поиск минимального (максимального) элемента.
Пример 31. В массиве X из 20 вещественных чисел поменять местами наибольшие и наименьшие элементы.
Уточним пространство решений. В массиве X может присутствовать несколько максимальных и минимальных элементов. Возможен неординарный случай для этой задачи, который состоит в том, что все элементы массива равны между собой. Переменные, используемые в программе, и их тип описаны в следующей таблице:
Эту задачу нужно решать с помощью двух последовательных просмотров массива X. Целью первого просмотра является вычисление наибольшего МАХ и наименьшего МIN значений элементов массива X. В начале просмотра значение первого элемента Х[1] считается одновременно наибольшим и наименьшим, что справедливо в том случае, если в массиве всего один элемент. Далее со второго элемента Х[2] и до последнего Х[20] сравниваются значение текущего элемента с MIN. Если значение текущего элемента меньше, то оно с этого момента считается минимальным. По окончании цикла в рабочей ячейке MIN окажется число, равное значению наименьшего элемента. Аналогично поступаем для нахождения МАХ.
Далее нужно сравнить между собой MIN и МАХ. Если эти величины равны между собой, то массив состоит из 20 равнозначных элементов. Следовательно, переставлять их местами нет необходимости. Если MIN?МАХ, то нужно наименьшим элементам присвоить значение МАХ, а наибольшим элементам присвоить значение MIN. Эти действия являются основой для второго просмотра массива X.
PROGRAM PR31;
VAR
X: ARRAY [ 1.. 20] OF REAL;
I: INTEGER;
MIN, MAX: REAL;
BEGIN
WRITELN(‘Введите массив X, из 20 вещественных чисел’);
FOR I := 1 ТО 20 DO READ(X[I]);
MIN :=Х[1];
МАХ :=Х[1];
FOR I := 2 ТО 20
DO BEGIN
IF MIN>X[I]
THEN MIN := X[I];
IF MAX THEN MAX := X[I];
END;
IF MIN <> MAX
THEN FOR I := 1 TO 20
DO BEGIN
IF MAX = X[I]
THEN X[I] := MIN
ELSE IF MIN = X[I]
THEN X[I]:=MAX;
END;
WRITELN(‘Элементы массива X имеют значения:’);
FOR I := 1 TO 20 DO WRITE(X[I]: 4:1,’ ‘);
WRITELN
END.
Источник: mojainformatika.ru
Найти минимальный элемент массива паскаль программа

НАХОЖДЕНИЕ МАКСИМАЛЬНОГО И МИНИМАЛЬНОГО ЭЛЕМЕНТА В МАССИВЕ
Прусаков И.В. 1
1 г. Новочеркасск, Гуманитарно-технический колледж ФГБОУ ВО «Южно-Российский государственный политехнический университет (НПИ) им. М.И. Платова»
Растеряев Н.В. (Новочеркасск, ФГБОУ ВО «Южно-Российский государственный политехнический университет (НПИ) им. М.И. Платова»)

1. Логинов В.И., Шемагина Л.Н. Основы алгоритмизации : учеб.-метод. пособие для студ. оч. заоч. обуч. техн. специальностей. – Н. Новгород : Изд-во ФГОУ ВПО «ВГАВТ», 2010. – 81 с.
2. Михалкович С.С., Логинов В.И., Шемагина Л.Н. Основы программирования : учеб.-метод. пособие для студ. 1 курса. – Ростов н/Д. : Изд-во ЮФУ, 2007. – 40 с.
Основу современной инженерной деятельности составляет умение ставить задачи, разрабатывать алгоритмы и получать решения, производить анализ полученных данных и делать выводы. Поэтому в своей профессиональной деятельности инженер должен уметь грамотно применять персональный компьютер, современное программное обеспечение для решения научных и инженерных задач.
Типичной задачей при обработке больших массивов данных является задача поиска максимума или минимума. Например, в списке успеваемости учеников класса найти самого прилежного. Иначе говоря, требуется выбрать наибольшее значение среднего балла и указать фамилию ученика. Или, в массиве среднесуточных температур окружающего воздуха за некоторый период наблюдений определить минимальное значение и указать дату самого холодного дня.
Цель работы: разработка программы нахождения максимального и минимального элемента в среде программирования Паскаль-ABC.
1) ознакомиться с алгоритмами поиска в массивах и методами их программной реализации;
2) освоить приемы программирования в интегрированной среде Паскаль-ABC;
3) разработать алгоритм и блок-схему нахождения максимального и минимального элемента в массиве;
4) создать программу нахождения максимального и минимального элемента в массиве и протестировать ее.
Объект исследования: алгоритмы поиска в массивах.
Предмет исследования: Паскаль-программа нахождения максимального и минимального элемента массива в среде Паскаль-ABC.
Алгоритмы поиска информации
Очень часто в реальной жизни нам приходится сталкиваться с задачей поиска информации в объеме данных. Например, поиск фамилии ученика в журнале, поиск нужного слова в словаре. Существует множество алгоритмов поиска, но из всего многообразия алгоритмов рассмотрим два основных и наиболее часто используемых на практике.
В алгоритмах поиска существует два возможных окончания работы: поиск может оказаться удачным – заданный элемент найден в массиве и определено его месторасположение, либо проведенный поиск может оказаться неудачным – необходимого элемента в данном объеме информации нет.
Несмотря на то, что целью поиска является значение элемента, алгоритм поиска в случае удачного окончания выдает так же и местоположение искомого элемента, например его номер в массиве, так как по номеру элемента можно однозначно восстановить и его значение.
Для оценки алгоритмов мы будем использовать такую характеристику, как сложность.
Пусть, например, человек ищет на полке книжку с определенным названием. Книги на полке стоят вразнобой, то есть не по алфавиту. Как будет действовать человек? Он будет сравнивать по порядку название каждой книги на полке с тем названием, которое ему нужно найти. В итоге он или найдет нужную ему книгу, или, просмотрев все книги на полке, не обнаружит нужной книги.
Этот пример передает суть алгоритма последовательного поиска в неупорядоченном массиве. Приведем его формальную запись.
Имеется одномерный массив a[1 … n], требуется найти элемент массива, равный P:
Алгоритм последовательного поиска в неупорядоченном массиве
Установить i = 1.
Если ai = P, алгоритм завершил работу успешно.
Увеличить i на 1.
Если i — n, то перейти к шагу 2. В противном случае алгоритм завершил работу безуспешно.
Оценим сложность алгоритма последовательного поиска. Естественно оценивать сложность по числу сравнений с искомым элементом. В худшем случае искомый элемент окажется на последнем месте или не будет найден, и тогда необходимо будет проделать n сравнений, то есть сложность алгоритма будет равна n. Такой поиск также называют линейным, так как он решает задачу поиска с линейной скоростью по количеству сравнений.
Усложним задачу. Пусть нам требуется найти минимальный элемент в неупорядоченном массиве. Оказывается, что и эта задача имеет линейную сложность, и для поиска минимального (максимального) элемента в неупорядоченном массиве требуется n – 1 сравнение. Запишем алгоритм поиска максимального элемента в текстовой (вербальной) форме.
Алгоритм поиска максимального элемента в неупорядоченном массиве
Установить счетчик равным 1 (i = 1).
Положим значение текущего максимума равным первому исследуемому элементу (max = a1).
Перейти к следующему элементу (увеличить i на единицу).
Если рассматриваемый элемент больше, чем текущий максимум (ai > max), то значение ai присвоить max.
Перейти к шагу 4.
Последовательный поиск не является самым эффективным алгоритмом поиска. Например, человеку нужно найти в русско-английском словаре перевод слова на английский язык. Если он будет искать его с помощью алгоритма последовательного поиска (просматривая все слова подряд), то он потратит очень много времени. На самом же деле интуитивно человек действует совсем по-другому.
Поиск слова в словаре наиболее приближен к алгоритму бинарного (двоичного) поиска, который также называют логарифмическим поиском, или методом деления пополам (дихотомией). Этот алгоритм достаточно эффективен, но использовать его можно только в случае, когда данные упорядочены. В этом алгоритме мы используем сравнение искомого элемента с серединным элементом и с помощью результата этого сравнения устанавливаем, в какой части данных находится искомый элемент.
Заметим, что даже если данные упорядочены, то использовать алгоритм бинарного поиска мы можем не всегда. Это касается тех случаев, когда мы не имеем доступа к любому элементу массива. Например, если данные поступают к нам последовательно.
Алгоритмы поиска максимального или минимального элемента массива
Алгоритмизация – это общая последовательность действий, которые необходимо выполнить для построения алгоритма решения задачи, в том числе – выделение конкретных шагов алгоритмического процесса, определение вида формальной записи для каждого шага и установление определенного порядка выполнения каждого шага [1]
Пусть поставлена следующая задача: по известным данным среднесуточных температур и дат найти максимальную или минимальную температуру и соответствующую ей дату.
Принцип поиска максимального или минимального элемента массива заключается в следующем. Первое, что необходимо сделать – создать массивы данных и дат. При этом сначала вводится параметр n – число элементов создаваемых массивов. Для ввода элементов массива используется цикл с параметром. Вводятся числовое значение и дата в формате ДД.ММ.ГГ.
Для определения того, будем находить максимальный или минимальный элемент, целочисленной переменной flag будем присваивать значения 1 или 0.
В дополнительную переменную заносится значение первого элемента массиваDan[ ], которое принимается за максимум (минимум); затем организовывается перебор оставшихся элементов массива, каждый из которых сравнивается с максимумом (минимумом); если текущий элемент массива оказывается больше (меньше), чем принятый за максимум (минимум), то этот элемент становится максимальным (минимальным). Таким образом, после завершения перебора элементов массива в дополнительной переменной окажется максимальное (минимальное) значение среди элементов массива.
Кроме этого введены еще две переменные imax и imin, которые будут использоваться для хранения номеров максимального и минимального элементов массива. После выхода из цикла будут найдены значения максимального или минимального элементов массива Dan[ ], а также их номера, по которым будут найдены соответствующие даты в массиве Tim[ ].
Представим разработанный выше алгоритм в виде блок-схемы.
Блок-схемой называется наглядное графическое изображение алгоритма, когда отдельные его этапы изображаются при помощи различных геометрических фигур — блоков, а связи между этапами (последовательность выполнения этапов) указываются при помощи стрелок. Типичные действия алгоритма изображаются геометрическими фигурами согласно ГОСТ 19.701-90.
Блок-схема алгоритма представлена на рис. 1.
Рис. 1. Блок-схема алгоритма нахождения максимального и минимального элемента

Интегрированная среда программирования Паскаль-ABC. Разработка и тестирование программы
На рис. 2 представлен скриншот разработанной программы в интегрированной среде программирования Паскаль-АВС.
Рис. 2. Скриншот программы
Система программирования Паскаль-ABC представляет собой диалект стандартного языка Паскаль. Система создавалась на факультете математики, механики и компьютерных наук ЮФУ как учебная среда программирования (автор – кандидат физико-математических наук, доцент кафедры алгебры и дискретной математики С.С. Михалкович) [2]. По мнению разработчиков этой системы, первоначальное обучение программированию должно проходить в достаточно простых и дружественных средах, в то же время эти среды должны быть близки к стандартным и иметь богатые и современные библиотеки подпрограмм.
На рис. 3 представлен скриншот результатов нахождения максимального значения температуры и соответствующей ей дате.
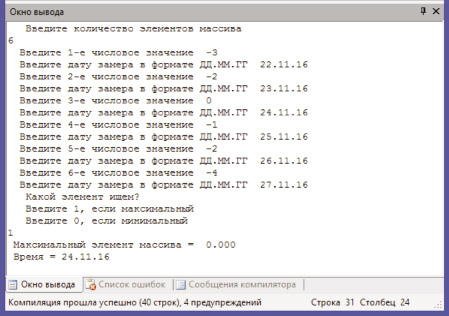
Рис. 3. Скриншот результатов нахождения максимального элемента
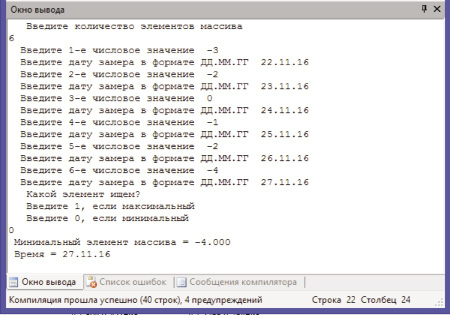
Рис. 4. Скриншот результатов нахождения минимального элемента массива
На рис. 4 представлен скриншот результатов нахождения минимального значения температуры в массиве и соответствующей ей дате.
В результате выполнения моей научно-исследовательской работы достигнута цель исследования – разработана программа нахождения максимального и минимального элемента в среде программирования Паскаль-ABC. Программа протестирована по двум ветвям вычислительного процесса: нахождение максимального и нахождение минимального элемента.
При этом я ознакомился с алгоритмами поиска информации в больших объемах данных. Освоил некоторые приемы программирования в интегрированной среде Паскаль-ABC. Разработал блок-схему и программу нахождения максимального и минимального элемента одномерного массива. Надеюсь, что полученные знания и навыки помогут мне успешно сдать экзамен по дисциплине информатика.
Источник: school-herald.ru
