Вычислить и вывести на экран в виде таблицы значения функции F на интервале
от Хнач. до Хкон. с шагом dX.
f = a*x*x + b, если x — 1 < 0 и b — x != 0;
f = x — a/x, если x — 1 > 0 и b + x == 0;
В остальных случаях x/c
где а, Ь, с — действительные числа.
Функция F должна принимать действительное значение, если выражение
(Ац ИЛИ Вц) МОД2 (Вц И Сц)
не равно нулю, и целое значение в противном случае. Через Ац, Вц и Сц обозна*
чены целые части значений а,fc,с, операции И, ИЛИ и МОД2 (сложение по мо*
дулю 2) — поразрядные. Значения а, 6, с, Хнач., Хкон., dX ввести с клавиатуры.
#include «stdafx.h» #include int main(int argc, char* argv[]) < double Xn, Xk, dX, a, b, c, y; printf(«Xn, Xk, dX, a, b, c: «); scanf(«%lf%lf%lf%lf%lf%lf», Xk, a, c); double x = Xn; printf(«———————-n»); printf(«| X | Y |n»); printf(«———————-n»); for(;x else < if(x — 1 >0 b + x == 0) < y = (x — a)/x; >else < y = x/c; >> if((int(a) | int(b)) ^ (int(b) |%.2f |%.2f |n», x, y); else printf(«|%.2f |%d |n», x, int(y)); > printf(«———————-n»); return 0; >
Привет.
Лекция 140: Тестирование программы, для любого x вычисляющей sin(x) как сумму ряда
Написал код, работает в Visual C++ 6.0. вроде.
Хотелось узнать правильно ли я сделал условие «(Ац ИЛИ Вц) МОД2 (Вц И Сц)»?
Источник: www.developing.ru
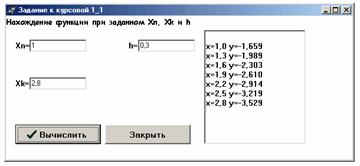
Вычисление значения функции y(x)
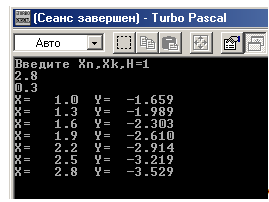
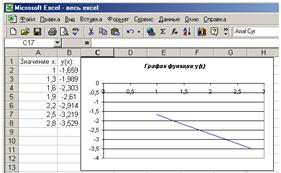
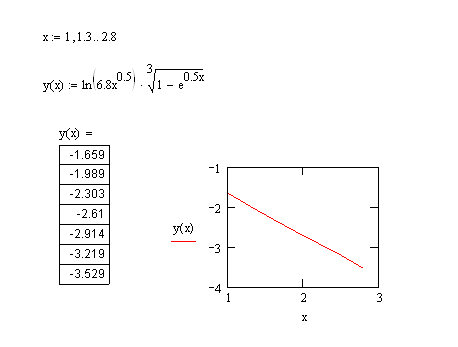
Вычислить значение функции y(x) на промежутке [1;2.8] с шагом h=0.3.
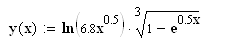
if z=0 then writeln(‘NO’) else
procedure TForm1.BitBtn1Click(Sender: TObject);
procedure TForm1.BitBtn2Click(Sender: TObject);
Вывод: т.к. ответы в Pascal,Excel,MathCAD и Delphi сошлись – решение верно.
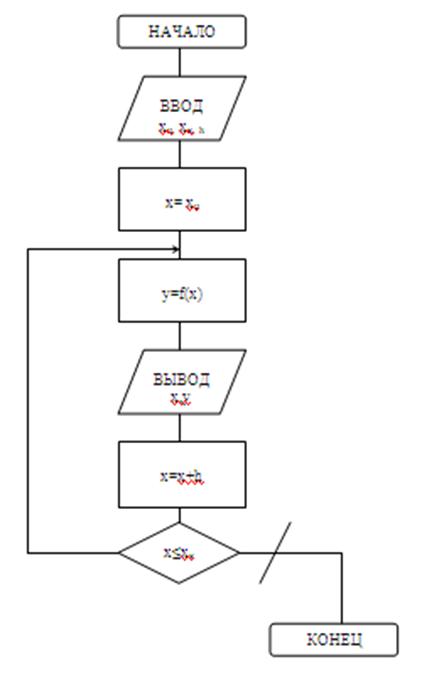
Блок-схема алгоритма решения задания №1.1
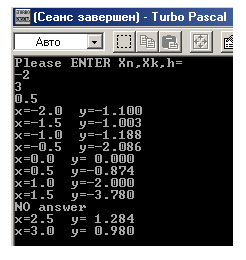
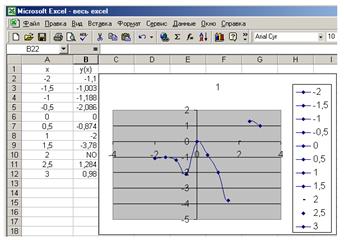
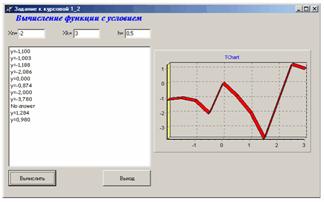
Вычислить значение функции y(x) с условием на промежутке [-2;3] с шагом h=0.5

writeln(‘Please ENTER Xn,Xk,h=’);
if x>2 then y:=sqr(cos(x))/(x-2)
компьютерный вычисление функция алгоритм
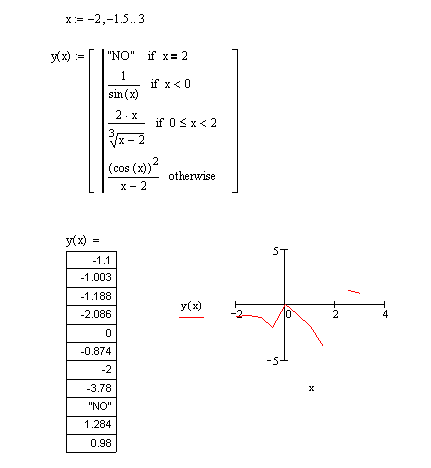
if x>2 then y:=sqr(cos(x))/(x-2);
C# ФУНКЦИИ И МЕТОДЫ | МЕТОД C# ЧТО ЭТО | ФУНКЦИИ C# ПРИМЕР | C# ОТ НОВИЧКА К ПРОФЕССИОНАЛУ | # 35
Вывод: т.к. ответы в Pascal, Excel, MathCAD и Delphi сошлись – решение верно.
Блок-схема алгоритма решения задания: 1.2
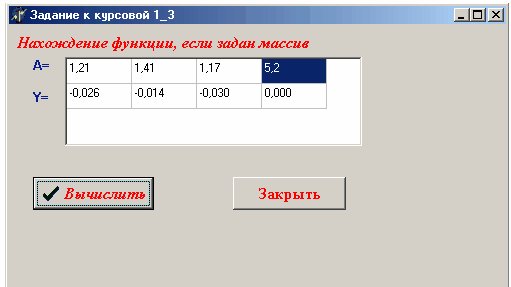
Нахождение функции, заданной условием:
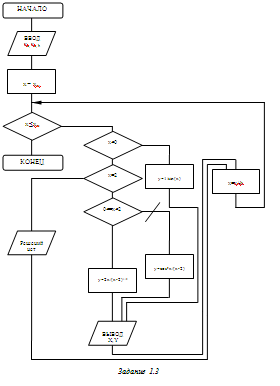
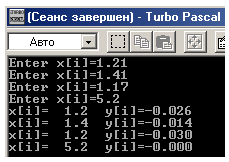
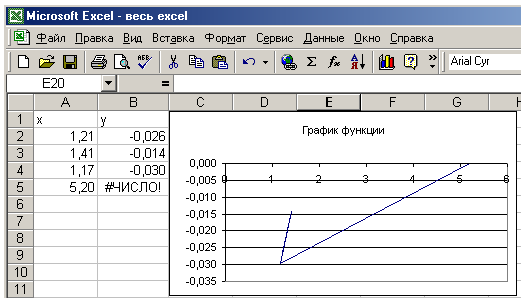
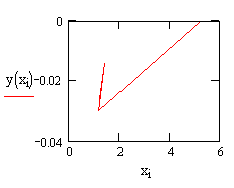
Вычислить функцию y(x) по заданному массиву x
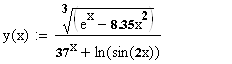

var x,y:array[1..n] of real;

var x,y:array[0..3]of real;
procedure TForm1.BitBtn2Click(Sender: TObject);
Вывод: т.к. ответы в Pascal,Excel,MathCAD и Delphi сошлись – решение верно.
Блок-схема алгоритма решения задания №1.3
Нахождение функции заданном массиве:
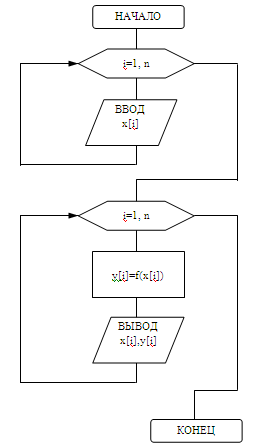
Найти сумму, если задана функция y(x), задан массив а, даны Xn, n, h.
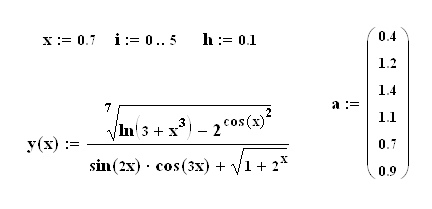
a:array [1..n] of Real;
Write(‘enter please Xn,h=’);
Write(‘enter please a[i]=’);
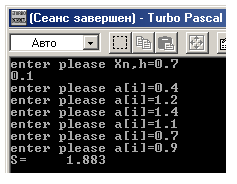


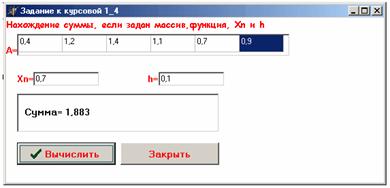
var a:array[0..5]of real;
memo1.Lines.Add(‘ Ñóììà= ‘+FormatFloat(‘0.000’,s));
procedure TForm1.BitBtn2Click(Sender: TObject);
Вывод: т.к. ответы в Pascal, Excel, MathCAD и Delphi сошлись – решение верно.
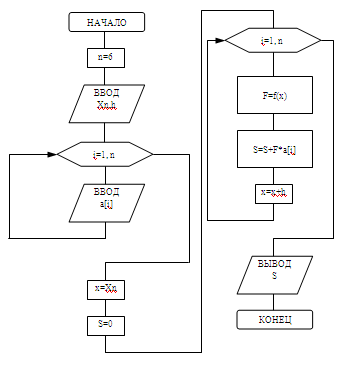
Блок-схема алгоритма решения задания №1.4
Нахождение функции, если дан x, h, n, задан массив:
Информация о работе «Вычисление значения функции y(x)»
Раздел: Информатика, программирование
Количество знаков с пробелами: 4822
Количество таблиц: 0
Количество изображений: 23
Похожие работы
. при построении итерационных методов решения уравнения =0. Например взяв за корень линейного интерполяционного алгебраического многочлена, построенного по значениям и в узле или по значениям и в узлах и , приходят соответственно к методу Ньютона и метода секущих , где — разделенная разность функций для узлов и . Другой подход к построению численных методов решения уравнения .

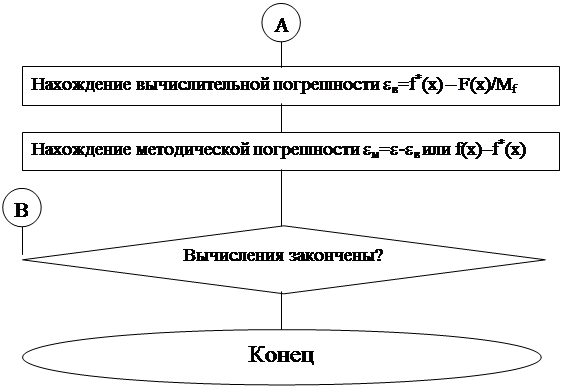

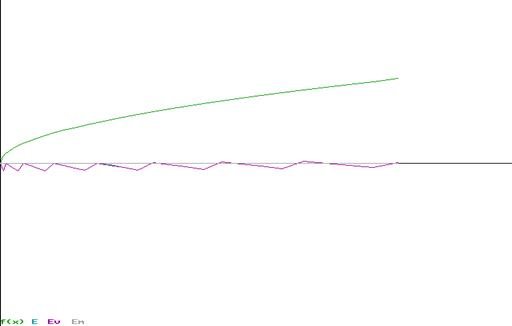
. вычисления значений этой функции на интервале аппроксимации. Приведение аргумента к интервалу аппроксимации является обязательным этапом как при использовании итеративных методов вычисления элементарных функций, так и при многочленной и рациональной аппроксимации. Этот прием позволяет сократить число операций необходимых для вычисления значения элементарной функции за счет уменьшения количества .
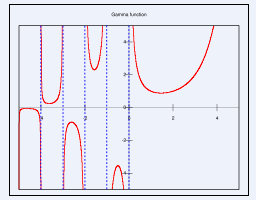
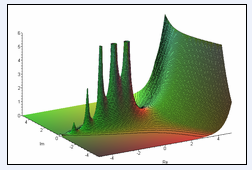
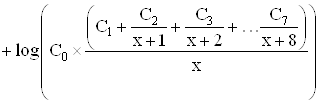
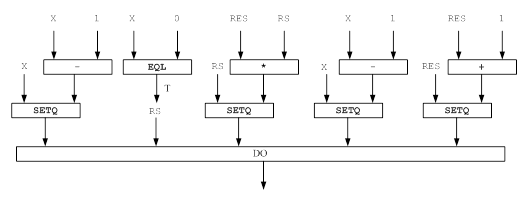
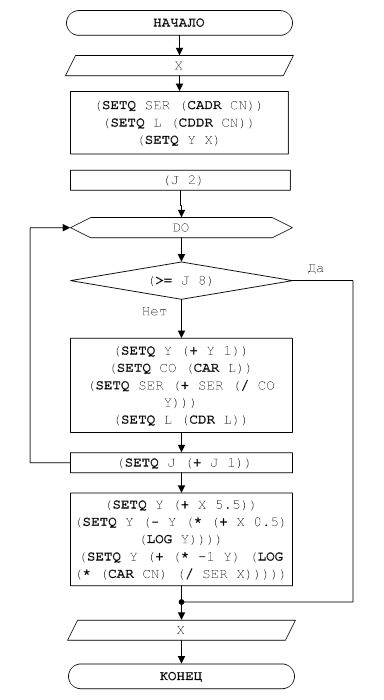
. к гамма-функции с положительным целым параметром, гамма-функции с положительным параметром, гамма-функции для множества точек. Созданная функциональная модель реализации основных способов вычисления гамма функции и ее программная реализация могут служить органической частью решения более сложных задач. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ и литературы 1. Бронштейн, И.Н. Справочник по .
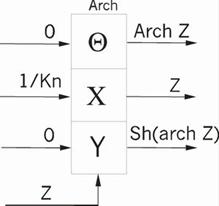
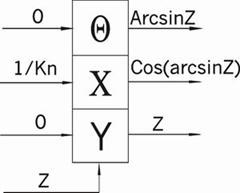
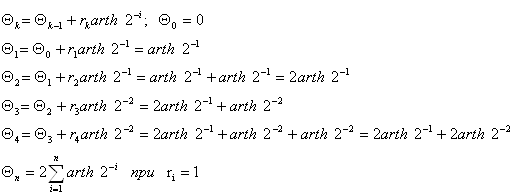
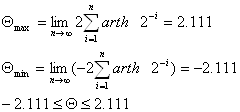
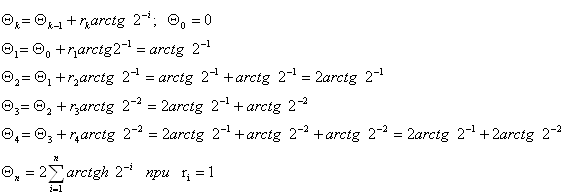
ть специализированный математический процессор для вычисления элементарных функций arcSin(Z) и arCth(Z). Эти функции можно реализовать методом Волдера «Цифра за цифрой», метод Меджита и др. Оба эти метода основаны на ряде итерационных формул, которые приведены в таблице 1.1. Основное их различие заключается в том, что в методе Меджита на первом этапе сразу рассчитываются все направляющие .
Источник: kazedu.com
ПРИМЕР ВЫПОЛНЕНИЯ Лабораторной РАБОТЫ
Схема алгоритма решения представлена на рис. 3. В блоке 2 вводятся исходные данные а, х, z. В блоке 3 вычисляется значение тангенса. В блоках 4 и 5 вычисляются значения функций у и р. а в блоке 6 осуществляется вывод вычисленных значений.

Если сравнивать язык Си с языком Pascal, то можно сделать вывод, что Си дает большую свободу действиям программиста. С другой стороны Си позволяет совершить ошибки, которые в Pascal совершить невозможно.
Методические рекомендации к выполнению лабораторной работы
Отчет к лабораторной работе должен содержать:
1. Постановка задачи
a) Список входных данных
b) Список выходных данных
c) Список промежуточных переменных
2. Разработка алгоритма решения задач
a) Разработка блок-схемы решения задачи.
b) Список функций
3. Разработка программного кода к алгоритму.
4. Проверка алгоритма (листинг)
a) Рассмотрение всех не стандартных ситуаций
b) Ограничения и допущения, если имеются
5. Ответы на контрольные вопросы.
Задание к лабораторной работе
Разработать алгоритм решения задачи (по вариантам) и написать программы на языках Си и ТР.
| Вариант задания | Расчетные формулы | Значения исходных данных |
| a=2cos(x-p/6)/2+sin 2 y b=1+z/3+z 2 /5 | x=1.426 y=-1.220 z=3.5 | |
| b= êx y/x ê*y-z/(y-x) g=(y-x)(y-z /(y-x)) /1+(y-x) 2 | x=1.825 y=18.225 z=-3.298 | |
| Y=e -bt sin(at+b)- S=bsin(at 2 cos2t)-1 | a=-0.5 b=1.7 t=0.44 | |
| W= -b2sin3(x+a)/x Y=cos2x3-x | a=1.5 b=15.5 x=-2.9 | |
| S=x 3 tg 2 (x+b) 2 +a/ Q=bx 2 -a/e ax -1 | a=16.5 b=3.4 x=0.61 | |
| R=x 2 (x+1)/b-sin 2 (x+a) S= +cos 2 (x+b) 3 | a=0.7 b=0.05 x=0.5 | |
| Y=sin 3 (x 2 +a) 2 — Z= (x+b) 3 | a=1,1 b=0,004 x=0,2 | |
| F= Z=m cos (bt sin t)+c | m=2 c=-1 t=1,2 b=0,7 | |
| y=b tg 2 x- d=ae -ax cos(bx/a) | a=3,2 b=17,5 x=-4,8 | |
| f=ln(a+x 2 )+sin 2 (x/b) z=e -cx | a=10,2 b=9,2 x=2,2 c=0,5 | |
| y= r= -b 2 sin 3 (x+a)/x | a=0,3 b=0,9 x=0,61 | |
| Z=cos 2 x 3 -x/ | a=0,5 b=3,1 x=1,4 | |
| U= F=e 2x ln (a+x) -b 3x ln(b-x) | a=0,5 b=2,9 x=0,3 | |
| Z= -c m ln (b-x) S =e -ax +e –b x | m=0,7 c=2,1 x=1,7 a=0,5 b=1,08 | |
| M= /1+tg 3 (n-k) H =sin k 2 -e -nk | n=3,8 k=0.9 1=0,78 | |
| S= M=cos 2 t 3 -x/ | v=1,72 t=-1,5 w=0.3 |
Контрольные вопросы
1. Опишите особенности линейной алгоритмической конструкции.
2. В чем сходства и различия языков Си/С++ и Turbo Pascal?
3. Сравните структуры программ, названия основных типов данных, описание раздела подключения библиотек, раздел описания переменных, функции ввода-вывода данных. Оформите в таблице сравнений:
| Си | Turbo Pascal |
| Структура программы | |
| Основные типы данных: Целый Вещественный…. |
Лабораторная работа № 3
ПРОГРАММИРОВАНИЕ ПРОЦЕССОВ с разветвляющейся структурой
Цель работы: овладение практическими навыками разработки алгоритмов и программ с разветвляющейся структурой на языках Turbo Pascal и С.
Теоретический материал
На практике редко удается представить схему алгоритма решения задачи в виде линейной структуры. Часто в зависимости от каких-либо значений промежуточных результатов необходимо организовать вычисления по одним или другим формулам. В зависимости от выполнения некоторого логического условия вычислительный процесс осуществляется по одной или другой ветви.
Алгоритм такого вычислительного процесса называется алгоритмом разветвляющейся структуры.
В качестве условия в разветвляющемся алгоритме может быть использовано любое понятное исполнителю утверждение, которое может соблюдаться (быть истинно) или не соблюдаться (быть ложно). Такое утверждение может быть выражено как словами, так и формулой. Таким образом, алгоритм ветвления состоит из условия и двух последовательностей команд.
В зависимости от того, в обеих ветвях решения задачи находится последовательность команд или только в одной, разветвляющиеся алгоритмы делятся на полные и не полные (сокращенные).
Стандартные блок-схемы разветвляющегося алгоритма приведены ниже:

Условные конструкции в ТР.
Разветвления в программах используют операторы перехода, условный и выбора варианта.
1) Оператор безусловного перехода GOTO позволяет изменять последовательность выполнения операторов в программе.
Формат записи оператора:
— имя метки, отличающей ту строку, на которую требуется выполнить переход.
Имя метки должно быть предварительно описано в разделе описания меток Label.
Неправильное использование в программе оператора GOTO усложняет читаемость программы.
2) Составной оператор (begin … end) представляет собой совокупность последовательно выполняемых операторов, заключенных в операторные скобки begin … end.
Этот оператор записывается следующим образом:
Составной оператор используется в тех случаях, когда в соответствии с правилами записи языка TURBO PASCAL можно записать только один оператор, в то время как требуется выполнить несколько операторов.
Отдельные операторы внутри составного оператора отделяются друг от друга точкой с запятой.Перед символом end точку с запятой можно не ставить, т. к. это слово не является отдельным оператором. Если же «;» будут поставлены, то они будут рассматриваться как пустой оператор, т. е. оператор не выполняющий никакого действия.Сам блок операторов программы является (можно считать) составным оператором, т. к. он тоже заключен в операторные скобки BEGIN. END, внутри которых располагается последовательность операторов, разделенных «;».
3) Условный оператор IF обеспечивает в зависимости от условия выбор одного из возможных действий.
Существует два варианта записи оператора:
a) Полный вариант:
If S then A else B;
b) Укороченный вариант:
где: S – условие (логическое выражение), которое проверяется на истинность.
A – оператор (только один!), выполняющейся, если выражение S – истинно.
B – оператор (только один!), выполняющейся, если выражение S – ложно.
Если вместо A или B требуется использовать несколько операторов, то применяется составной оператор (BEGIN. END).
Примеры использования оператора IF приведены в Приложении 1.
4) Оператор выбора варианта Case … of … end.
Используется для обработки ситуаций с несколькими вариантами решения (путем выбора одного из нескольких операторов), выбираемых в зависимости от некоторого выражения, называемого селектором.
Существует две формы записи этого оператора:
| 1) Case S of c1: ; c2: < оператор 2>; …………………. cN: < оператор N>else < оператор>end; | 2) Case S of c1: ; c2: < оператор 2>; …………………. cN: < оператор N>end; |
где S – выражение порядкового типа, значение которого вычисляется;
сl,c2. сN—это константы или метки, с которыми сравниваются значения выражения селектора (S). Они должны быть одного гита с селектором.
Выбор оператора определяется совпадением значения селектора S и константы (метки сl,c2. cN), стоящей перед оператором.
< оператор 1 >, < оператор 2 >, < оператор N >— один оператор, либо составной оператор (begin. end),
< оператор >— оператор, который выполнится, если значение выражения S не совпадет ни с одной из меток (констант) сl,c2. cN.
Примеры использования оператора IF.
a) IF p>0.5 THEM GOTO 15;
Ключевое слово ELSE всегда относится к ближайшему ему IF.
Пример 1. Вычислить и вывести на экран значение заданной функции
Источник: zdamsam.ru