С клавиатуры вводятся целые числа до первого числа, которое меньше двух. Написать программу, которая определяет сколько простых чисел было введено.
Простые числа — это натуральные числа больше единицы, которые делятся нацело только на единицу и на себя. Например, число 3 простое, так как нацело делится только на 1 и 3. Число 4 сложное, так как нацело делится не только на 1 и 4, но также на число 2.
Перебор делителей – это алгоритм, применяемый для определения, является ли натуральное число простым, или оно является сложным, то есть составным. Алгоритм перебора делителей заключается в последовательном делении заданного натурального числа на все целые числа, начиная с двойки и заканчивая значением меньшим или равным квадратному корню из тестируемого числа.
Если хотя бы один делитель делит исследуемое число без остатка, значит это число является составным. Если ни одного такого делителя не находится, то число признается простым.
- count — счетчик простых чисел;
- number — очередное введенное число.
Пока введенное число больше 1, проверять его на простоту по следующему алгоритму:
Сумма цифр трехзначного числа. Решение задачи на Python
- Если число делится на любой делитель от 2 до квадратного корня из себя, то оно составное.
- Если число так и не разделилось нацело ни на один из делителей, то оно простое, следовательно, увеличиваем счетчик простых чисел.
var number, count, i: integer; flag: boolean; begin count := 0; readln(number); while number > 1 do begin flag := TRUE; for i := 2 to round(sqrt(number)) do if number mod i = 0 then begin flag := FALSE; break; end; if flag then count := count + 1; readln(number); end; writeln(‘Простых чисел: ‘, count); end.
Пример выполнения программы:
56 31 18 15 7 101 0 Простых чисел: 3
Источник: pas1.ru
Студия Компьютерного Мастерства

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1 при n = 1;
F(n) = n × F(n − 1), если n > 1.
Чему равно значение выражения F(2023) / F(2020)?
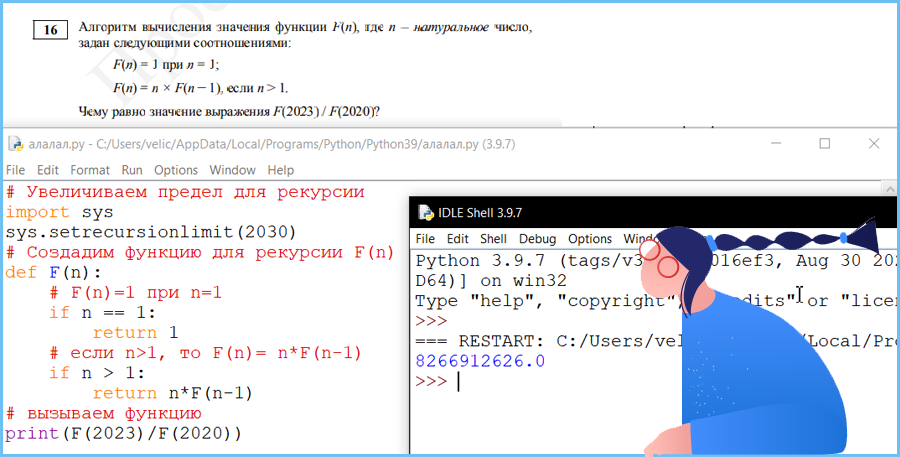
Вариант программы 1
Лимит рекурсии по умолчанию в Python является 1000, вы получите ошибку « RecursionError: максимальная глубина рекурсии превышена в сравнении »
Это может быть исправлено, увеличивая предел рекурсиона в Python, ниже – фрагмент о том, как вы можете увеличить предел рекурсии.
import sys
sys.setrecursionlimit(2030)
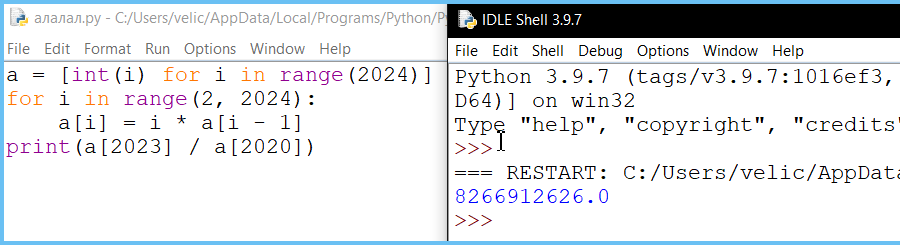
Вариант программы 2
Алгоритмы, опирающиеся на несколько предыдущих значений
Задание 6 (Решу ЕГЭ)
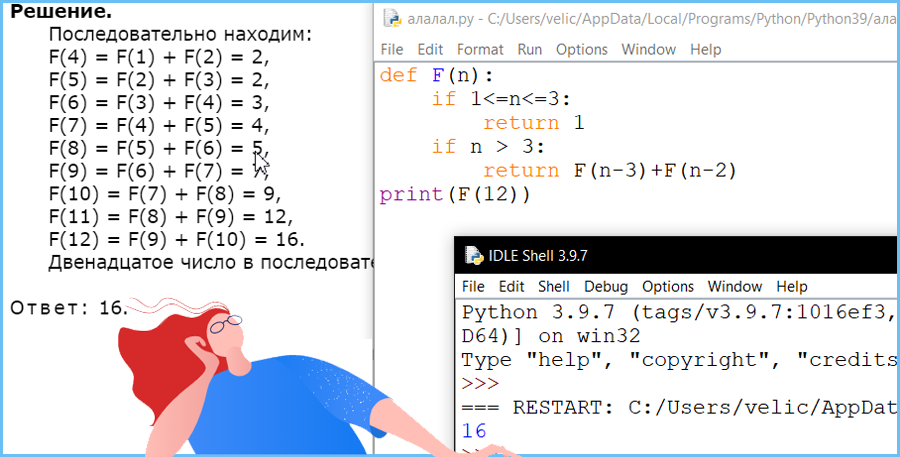
Последовательность чисел Падована задается рекуррентным соотношением:
F(n) = F(n–3) + F(n–2), при n >3, где n – натуральное число.
Числа Фибоначчи. Решение задачи на Python
Чему равно двенадцатое число в последовательности Падована?
В ответе запишите только натуральное число.
Задание 6 (Решу ЕГЭ)
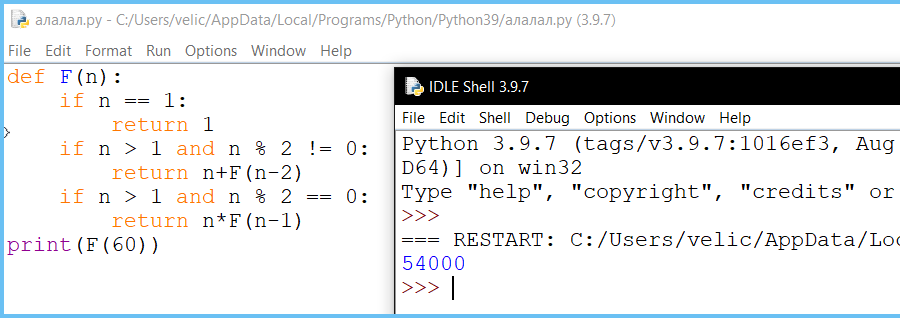
Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
F(n) = n + F(n − 2), если n — нечётно, и n > 1;
F(n) = n × F(n − 1), если n — чётно.
Чему равно значение функции F(60)?
Алгоритмы, опирающиеся на несколько предыдущих значений
Задание 6 (Решу ЕГЭ)
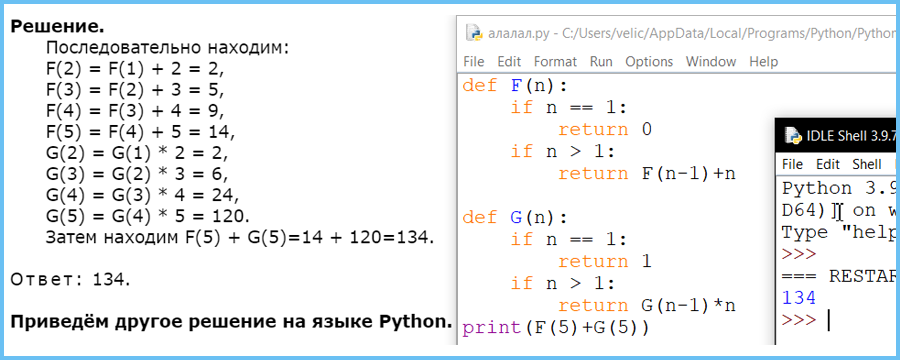
Алгоритм вычисления значения функции F(n) и G(n), где n – натуральное число, задан следующими соотношениями:
F(n) = F(n–1) + n, при n >1
G(n) = G(n–1) * n, при n >1
Чему равно значение функции F(5) + G(5)?
В ответе запишите только натуральное число.
Сложные задачи
Задание 6 (Поляков ЕГЭ)
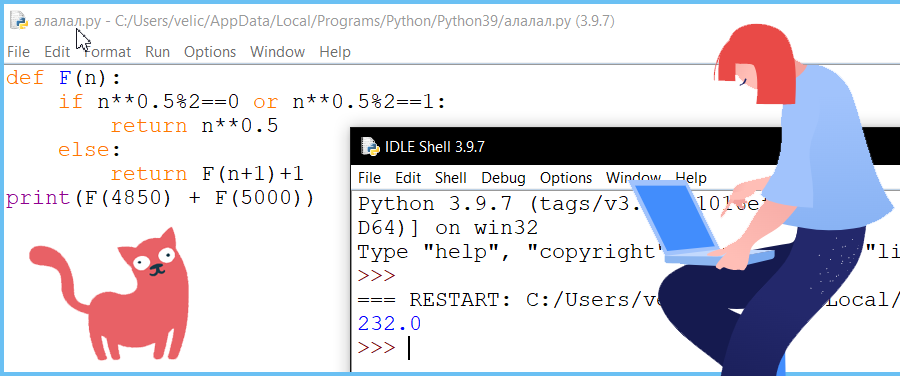
(№ 5604) (А. Куканова) Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями: F(n) = sqrt(n), если sqrt(n) – натуральное число, F(n) = F(n + 1) + 1, если sqrt(n) – дробное число. Чему равно значение выражения F(4850) + F(5000)?
При делении натурального числа на 2 мы получаем в остатке (%) или 0 или 1 (чётные и нечётные числа), таким образом проверяем, если корень дает четное или нечётное целое число, то выводим корень этого числа во всех остальных случаях применяет функцию F(n+1)+1
sqrt(n) запишем как n**0.5, что бы не подключать дополнительный математический модуль из библиотеки
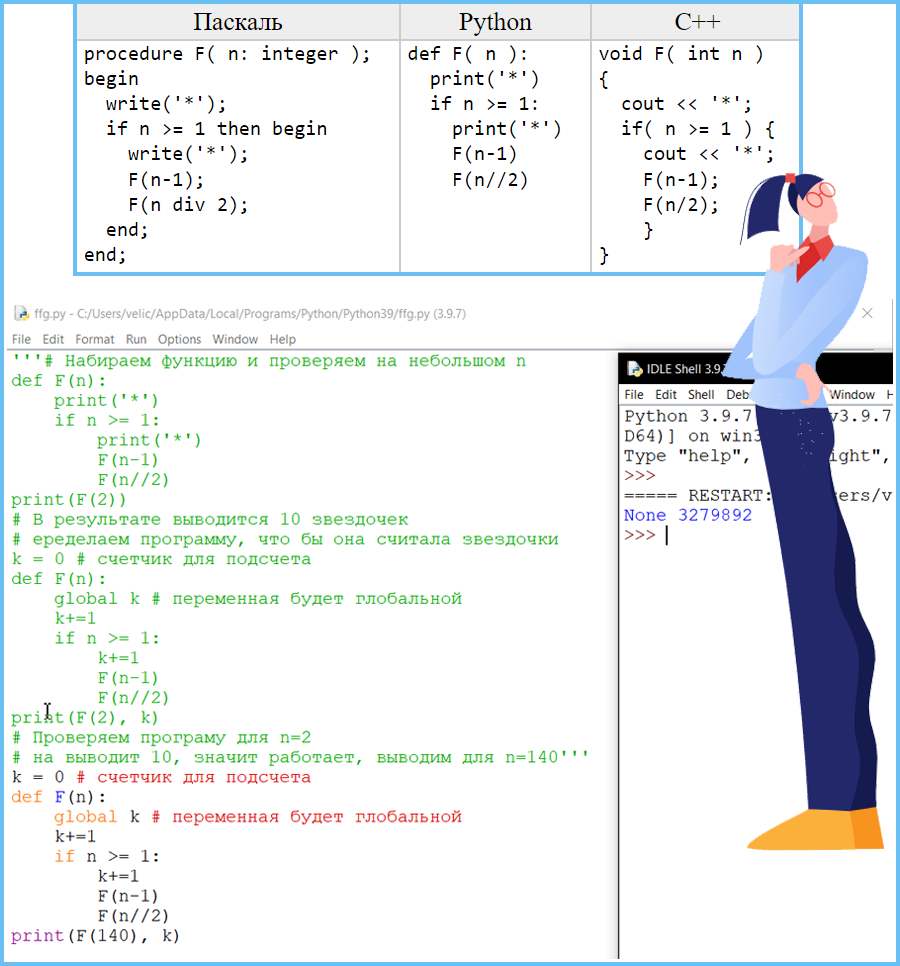
Задание 6 (Поляков ЕГЭ)
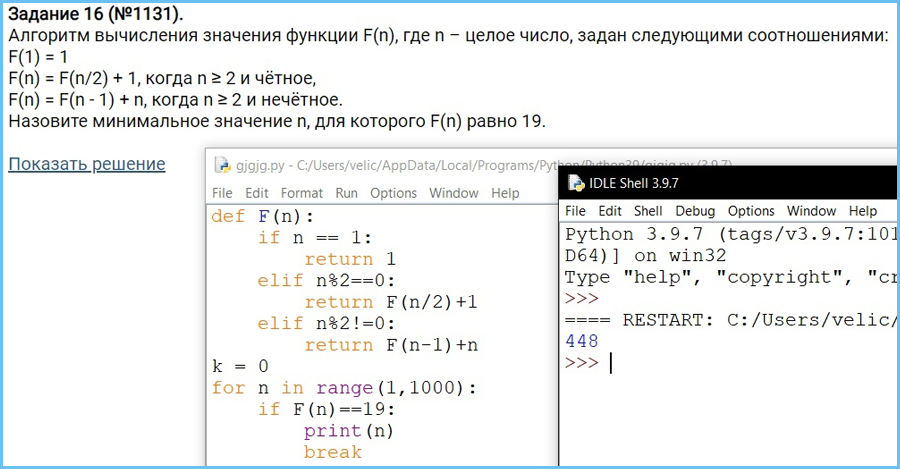
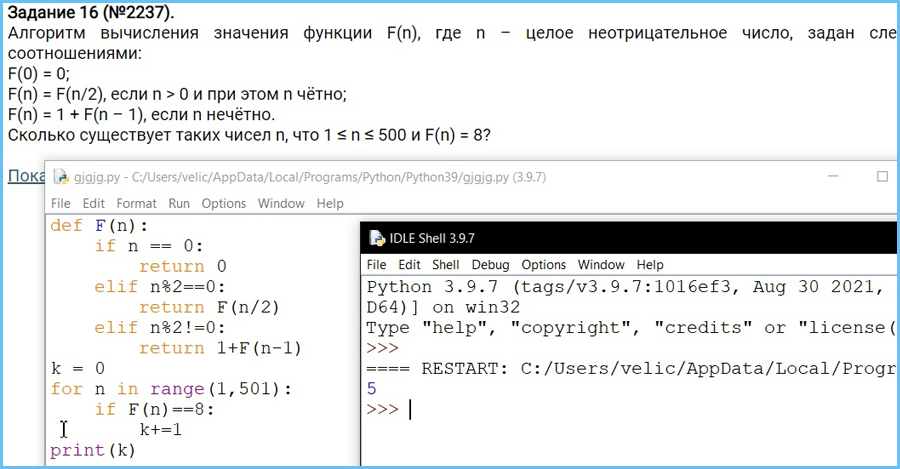
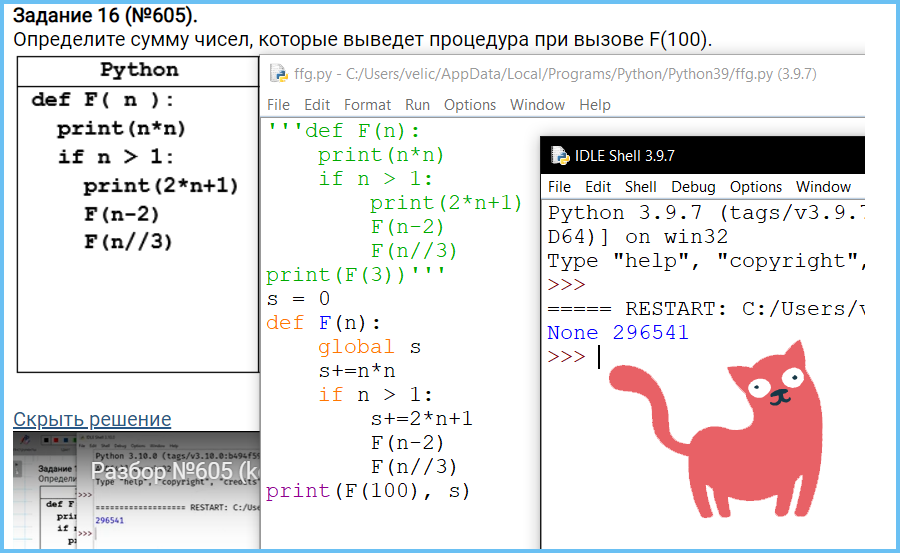
Определите, сколько символов * выведет эта процедура при вызове F(140):
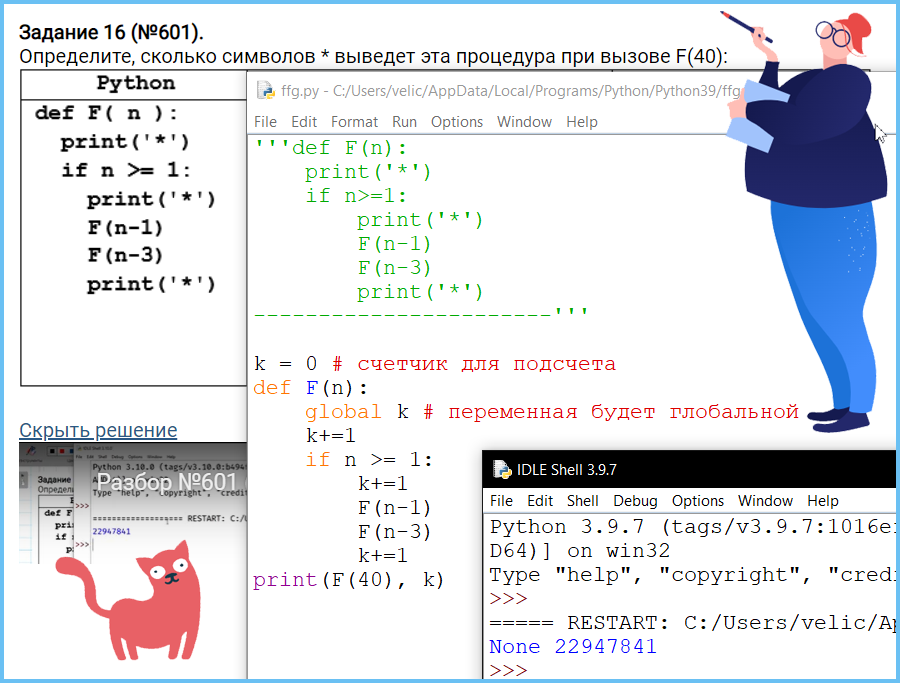
Алгоритмы, опирающиеся на несколько предыдущих значений
Задание 6 (Поляков ЕГЭ)
(№ 5604) (А. Куканова) Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = n!, если n ≥ 5000,
F(n) = 2 · F(n + 1) / (n + 1), если 1 ≤ n < 5000.
Чему равно значение выражения 1000 · F(7) / F(4)? Примечание.
Факториал числа n, который обозначается как n!, вычисляется по формуле n!=1·2·…·n.
Модуль math – один из наиважнейших в Python. Этот модуль предоставляет обширный функционал для проведения вычислений с вещественными числами (числами с плавающей точкой). Для использования этих функций в начале программы необходимо подключить модуль, что делается командой import:
# программный код
import math
num1 = math.sqrt(2) # вычисление корня квадратного из двух
Как можно заметить из примера выше, для вызова функции мы вынуждены указывать название модуля и символ точки. С другой стороны, если функции используются достаточно часто, то такой вызов (постоянное указание названия модуля и символа точки) может усложнить программу и сделать её менее читабельной. Для того, чтобы не указывать название модуля и символ точки при вызове функций, мы пишем следующий код:
# программный код
from math import *
Если нужно использовать только некоторые функции модуля, то мы можем импортировать только их следующим образом: from math import sqrt, ceil, factorial
Источник: css-info.ru
Разбор задания №16 по информатике из демоверсии 2021. Решаем двумя способами. С помощью рекурсии и циклов в Python.
Рекурсивной называется процедура, вызывающая сама себя.
Для решения этой задачи нам необходимо написать программу, которая будет содержать условия. При выполнении этих условий, будут выполняться команды. В задаче эти условия и команды которые нужно выполнять нам даны. Нужно все это просто написать на языке программирования. Мы будем писать на Питоне.
Пройдемся по строкам нашей программы:
- def f(n): — объявили функцию f(n);
- if n == 1: — задаем условие, если f(n) = 1, то выполняется следующее действие;
- return 1 — означает что n = 1. Оператор return возвращает значение 1 функции;
- elif n % 2 == 0: — иначе проверяется условие, если f(n) — четное, то выполняется следующее действие;
- return n + f(n-1) — оператор return возвращает значение n + f(n-1) функции; т.е. f(n) = n + f(n − 1);
- else: — иначе, если число нечетное, то выполняется следующее действие;
- return 2 * f(n-2) — оператор return возвращает значение 2 * f(n-2) функции; т.е. 2 * f(n − 2)
- print(f(26)) — вызываем функцию f(n), где n = 26. И выводим результат на экран.
Ответом к этому заданию будет число — 4122
16 задание я советую решать именно так, а следующий способ с применением циклов, я написала для вас, чтобы вы смогли понять что же такое рекурсия и какие шаги проделывает наша программа, прежде чем получить число 4122
Решение с применением цикла
Этот способ стоит изучать только для того чтобы понять каким образом работает рекурсия в нашей задаче. В общем для тех кто любопытный и хочет разобраться. А вообще достаточно научится писать программу с функцией которая вызывает сама себя.
Советую написать этот код в компилятор и посмотреть что получится!
Строки — print(«Если n =», i, «a =», a) , в данной программе функционала никакого не несут, они нужны просто для наглядности. Чтобы вы видели как меняются результат на каждом шаге. В range мы пишем n + 1, для того чтобы цикл прошел по числу 26.
Источник: dzen.ru