Как найти принадлежит ли точка заштрихованной области
Пусть необходимо определить попадает ли заданная точка с координатами (x,y) в заданную область:
В данном случае, очевидно, что точка (x,y) попадает на линию графика, если у=x. Точка попадает в закрашенную область, лежит выше линии графика, если y>x. Наконец, точка (x, y) лежит ниже линии графика, если yif y>x then writeln(‘Да, попадает’) else writeln(‘Нет’);
Аналогично, точка (x, y) попадает в закрашенную область,
if y>x*x then writeln(‘Да, попадает’) else writeln(‘Нет’);
Рассмотрим попадание точки в круг. Уравнение окружности: x2+y2=r2, в представленном на рисунке случае r=1.
Точка (x, y) лежит на линии окружности, если расстояние до нее
, если l=r. Если l>r, то точка лежит вне окружности. Если l
readln(x,y);
l:=sqrt(x*x+y*y);
if l else writeln(‘Нет’);
Для закрашенной области программный код имеет вид:
readln(x,y); l:=sqrt(x*x+y*y); if (l<1) and (y>x*x) then writeln(‘Да, попадает’) else writeln(‘Нет’);
Использование связок and, or весьма эффективно:
33 Задача: Принадлежит ли точка кругу с центром в начале координат?
readln(x,y); l:=sqrt(x*x+y*y); if (l<1) and ((x>0) and (y>Sin(x)) or (x<0) and (y
В демоверсии ЕГЭ 2010 была следующая графическая задача:
Требовалось написать программу, при выполнении которой с клавиатуры считываются координаты точки на плоскости (x, y — действительные числа) и определяется принадлежность этой точки заданной заштрихованной области (включая границы). Программист торопился и написал программу
программа на паскале:
var x,y:real; begin readln(x,y); if x*x+y*y >= 4 then if x > -2 then if y < -x then write(‘принадлежит’) else write(‘не принадлежит’) end.
программа на бэйсике
INPUT X,Y IF X*X=Y*Y>=4 THEN IF X>=-2 THEN IF Y
программа на Си
void main(void) < float x,y; scanf(«%f%f»,y); if (x*x+y*y>=4) if (x>-2) if (y
Последовательно выполните следующее:
1. Приведите пример таких чисел x,y, при которых программа неверно решает поставленную задачу.
2. Укажите, как нужно доработать программу, чтобы не было случаев её неправильной работы. (Это можно сделать несколькими си достаточно указать любой способ доработки исходной программ:
В соответствии с приведенными программами нарисуем блок-схему алгоритма
из которой сразу видно, где программист сделал ошибку. Конструкция Else всегда отностится к ближайшему If. При X*X+Y*Y
var x,y:real; begin readln(x,y); if (x*x+y*y>=4) and(x>=-2) and (y<-x) then write(‘принадлежит’) else write(‘не принадлежит’) end.
Однако, эта доработка также не верна!
Она не учитывает тот факт, что Y≥0. Приведенная программа будет считать лишние точки принадлежащими закрашенной области.
Правильная доработка программы:
var x,y:real; begin readln(x,y); if (x*x+y*y>=4) and(x>=-2) and (y<-x) and (y>=0) then write(‘принадлежит’) else write(‘не принадлежит’) end.
Определение принадлежности точки плоскости заштрихованной области на графике
Определение принадлежности точки плоскости заштрихованной
области на графике
В задачах этого вида дан рисунок координатной плоскости, и некоей закрашенной/заштрихованной области, ограниченной набором прямых и кривых. Нужно определить, принадлежит ли точка с координатами (x,y) этой области или нет.
Так как уравнения всех границ указаны на графике, задачи этого вида требуют понимания того, какой знак нужно поставить в соответствующем неравенстве. плоскость бейсик паскаль программа
Выписав все неравенства, которые «ограничивают» закрашенную/заштрихованную область, и объединив их логической операцией «И» («AND»), получим условие, которое должна проверять программа. Если условие выполняется — точка принадлежит области, если не выполняется — не принадлежит.
Так, если искомую область ограничивает вертикальная прямая линия, то в общем виде уравнение этой прямой выглядит как
где а — то значение на оси х, через которое проходит данная прямая (напомним, что если эта прямая совпадает с осью у, то уравнение прямой будет «х=0»).
Так как ось х направлена вправо (на что указывает «стрелка»), то все значения координаты x справа от нашей прямой будут больше числа а. А все значения координаты х слева от нашей прямой («х=а») будут меньше а. Получаем, что если закрашенная/заштрихованная область лежит справа от прямой «х=а», то все ее точки удовлетворяют условию «х>=а», а если слева — то условию «х =a v вместо «х>а»): так как на графике все прямые и кривые нарисованы сплошной линией, то закрашенная/заштрихованная область включает свои границы. Поэтому мы и пишем «больше или равно» или «меньше или равно». Строгие неравенства (строго больше/меньше) нужно было бы использовать, если бы границы области были бы нарисованы пунктиром.
Все остальные прямые и кривые, ограничивающие область, уравнения которых сводятся к виду «у=какое-то_выражение» нужно рассматривать с позиции у-координаты (ведь это именно она стоит в левой части уравнения). Так как ось «у» направлена вверх, то все точки, которые лежат выше прямой/кривой, должны удовлетворять условию «у>=это_выражение», а все точки, лежащие ниже нее- условию «у =это_выражение», а если ниже — то условию » у 2 +y 2 =R 2 «
где R — радиус этой окружности.
Как вы, вероятно, понимаете, левая часть этого уравнения (х 2 +у 2 ) задает квадрат расстояния от начала координат до точки плоскости. Для всех точек нашей окружности это расстояние равно ее радиусу R. Именно в этом смысл уравнения окружности. Значит, для всех точек внутри окружности, включая саму окружность, это расстояние будет меньше R. Это можно выразить неравенством
А для всех точек снаружи окружности неравенство будет «x 2 +y 2 >R 2 «. Рассмотрим пример:
В данной задаче закрашенную область ограничивают три прямые линии: горизонтальная (ее уравнение «у=2»), наклонная (ее уравнение «у=х») и вертикальная (она совпадает с осью у, ее уравнение «х=0»).
Относительно горизонтальной прямой закрашенная область находится снизу, поэтому знак неравенства должен быть «меньше или равно» — «у =х».
Относительно вертикальной прямой закрашенная область находится справа, поэтому знак неравенства должен быть «больше или равно» — «x>=0».
Итого получаем условие:
на Паскале и на Бейсике:
На Бейсике и Си, в данном случае, скобки можно не писать. Но лучше приучиться писать их всегда, чтобы не задумываться каждый раз, нужны они или нет.
В этом примере задача была очень простой — закрашенная область была ограничена только прямыми линиями. Если же область ограничена кривыми (или хотя бы одной кривой), то в список условий обычно приходится добавить еще одно или два условия- ведь кривая может в стороне от закрашенной области изменять свое направление.
И тогда получится, что набора ограничений, который мы написали, просто перечислив линии, ограничивающие область, может оказаться недостаточно. Рассмотрим пример:
Линий, ограничивающих закрашенную область, три: вертикальная прямая х=1,5, горизонтальная прямая у=0 и кривая у=х 2 .
Руководствуясь вышеприведенными рассуждениями, строим систему условий:
х =0 (закрашенная область лежит выше горизонтальной прямой) и у 2 (закрашенная область лежит ниже кривой).
Однако, этих условий недостаточно, чтобы ограничить закрашенную область.
Например, чтобы это понять, можно воспользоваться методом «штриховки»: для каждого условия заштрихуем разными способами область плоскости, удовлетворяющую этому условию. Там, где все штриховки пересекутся (наложатся одна на другую), все условия будут выполняться.
На рисунке видно, что все три штриховки накладываются друг на друга не только на закрашенной области, но и в области, на которую указывает пунктирная стрелка. Этот эффект объясняется очень просто — правило, которое позволяет задать область плоскости, просто перечислив уравнения ограничивающих линий с соответствующим знаком, действует только в том случае, если эти линии не изменяют своего направления (т.е. функции, графиками которых они являются — возрастающие или убывающие). В случае с параболой у=х это не так — слева от начала координат функция у=х2 убывает, а справа — возрастает, в результате чего наши условия неверно ограничивают закрашенную область.
Для исправления этой ошибки нужно добавить еще одно условие. Например, «х>=0».
Таким образом, правильным ответом в данном случае будет: На Паскале и Бейсике:
(х>=0) AND (x =0) AND (y 0, х =0 и y 2 , которые должны выполниться одновременно.
Изучаем предложенную программу и замечаем, что одного условия — х>=0 — не хватает. Без него под систему условий х =0 и у 2 подпадают также точки под параболой слева от оси OY и сверху от оси ОХ. Чтобы ответить на первый вопрос задачи (и получить свой первый балл), вычислим какую-нибудь точку из этой области. Она должна быть сверху от оси ОХ (значит, у>0), слева от оси OY (значит, х 2 ). Возьмем какую-нибудь точку на оси ОХ такую, что х =0 и у 2 . Например, 0,5.
Отвечаем на первый вопрос: х=-1y=0,5
Теперь постараемся исправить программу. Основное (и очевидное), что нужно в программу добавить — проверку еще одного условия (х>0).
Однако за такое решение мы получим еще только один балл (из двух возможных).
Второй балл нам не дадут, потому что в программе «спрятана» не одна ошибка, а две — во-первых, программа не проверяет условие х х 2 и при х>1.5). В этих случаях программа просто ничего не выдает в качестве ответа (а должна выдавать «не принадлежит»).
Чтобы исправить эту ошибку нужно либо добавить еще столько ELSE, сколько не хватает (в нашем, исправленном, случае — еще три).
Либо (что гораздо проще и короче) записать условие принадлежности точки области через сложное условие (через логическое И). Рекомендуемый ответ должен выглядеть так:
Уравнение окружности.
Аналитическая геометрия дает единообразные приемы решения геометрических задач. Для этого все заданные и искомые точки и линии относят к одной системе координат.
В системе координат можно каждую точку охарактеризовать ее координатами, а каждую линию – уравнением с двумя неизвестными, графиком которого эта линия является. Таким образом геометрическая задача сводится к алгебраической, где хорошо отработаны все приемы вычислений.
Окружность есть геометрическое место точек с одним определенным свойством (каждая точка окружности равноудалена от одной точки, называется центром). Уравнение окружности должно отражать это свойство, удовлетворять этому условию.
Геометрическая интерпретация уравнения окружности – это линия окружности.
Если поместить окружность в систему координат, то все точки окружности удовлетворяют одному условию – расстояние от них до центра окружности должно быть одинаковым и равным окружности.
Окружность с центром в точке А и радиусом R поместим в координатную плоскость.
Если координаты центра (а;b), а координаты любой точки окружности (х; у), то уравнение окружности имеет вид:
Если квадрат радиуса окружности равен сумме квадратов разностей соответствующих координат любой точки окружности и ее центра, то это уравнение является уравнением окружности в плоской системе координат.
Если центр окружности совпадает с точкой начала координат, то квадрат радиуса окружности равен сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:
Следовательно, любая геометрическая фигура как геометрическое место точек определяется уравнением, связывающим координаты ее точек. И наоборот, уравнение, связывающее координаты х и у, определяют линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.
Примеры решения задач про уравнение окружности
Задача. Составить уравнение заданной окружности
Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.
Решение.
Обратимся к формуле уравнения окружности:
R 2 = (x- a ) 2 + (y- b ) 2
Подставим значения в формулу.
Радиус окружности R = 4
Координаты центра окружности (в соответствии с условием)
a = 2
b = -3
Получаем:
(x — 2 ) 2 + (y — ( -3 )) 2 = 4 2
или
(x — 2 ) 2 + (y + 3 ) 2 = 16 .
Задача. Принадлежит ли точка уравнению окружности
Проверить, принадлежит ли точка A(2;3) уравнению окружности (x — 2) 2 + (y + 3) 2 = 16.
Решение.
Если точка принадлежит окружности, то ее координаты удовлетворяют уравнению окружности.
Чтобы проверить, принадлежит ли окружности точка с заданными координатами, подставим координаты точки в уравнение заданной окружности.
В уравнение ( x — 2) 2 + ( y + 3) 2 = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3
Проверим истинность полученного равенства
( x — 2) 2 + ( y + 3) 2 = 16
( 2 — 2) 2 + ( 3 + 3) 2 = 16
0 + 36 = 16 равенство неверно
Таким образом, заданная точка не принадлежит заданному уравнению окружности.
Принадлежит ли точка кругу?
Определить, принадлежит ли точка с координатами (x; y) кругу радиуса R с центром в начале координат.
Пользователь вводит координаты точки и радиус круга.
Если выбрать точку на координатной плоскости, то можно увидеть, что проекции ее координат на оси x и y являются катетами прямоугольного треугольника. А гипотенуза этого прямоугольного треугольника как раз показывает расстояние от начала координат до точки. Таким образом, если длина гипотенузы будет меньше радиуса круга, то точка будет принадлежать кругу; иначе она будет находится за его пределами.
Длину гипотенузы вычисляется по теореме Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Откуда гипотенуза равна квадратному корню из суммы квадратов катетов.
Пример выполнения программы:
Обратите внимание, можно вводить отрицательные координаты. При возведении в квадрат все-равно будет получено положительное число.
Круг:
(x — x0)^2+(y-y0)^2 < R^2 — множество точек внутри круга
(x — x0)^2+(y-y0)^2 > R^2 — множество точек вне круга
R — радиус круга, x0, y0 — координаты центра
Эллипс:
((x — x0)/a)^2+((y-y0)/b)^2 < 1 — множество точек внутри эллипса
((x — x0)/a)^2+((y-y0)/b)^2 > 1 — множество точек вне эллипса
a, b — радиусы эллипса
Прямые:
x < 0 — множество точек левее оси 0Y
x > 0 — множество точек правее оси 0Y
y < 0 — множество точек ниже оси 0X
y > 0 — множество точек выше оси 0X
ax+by < c множество точек ниже прямой, заданной уравнением ax+by = с
ax+by > c множество точек выше прямой, заданной уравнением ax+by = с
Для вашей задачи:
1. Находите нужные коэффициенты для всех прямых и кривых.
2. Выясняете для каждого уравнения знак, который получается при попадании точки в заштрихованной области
3. Создаёте набор тестов для точки.
Например для зоны B:
Точка должна быть внутри круга, вне эллипса и выше прямой, то есть должны выполняться следующие неравенства (коэффициенты a, b x0, y0 для каждого неравенства свои):
(x — x0)^2+(y-y0)^2 < R^2
((x — x0)/a)^2+((y-y0)/b)^2 > 1
ax+by > c
Дальше для тестовой точки проверяете неравенства, и если они все правильные — точка принадлежит заштрихованной области.
Источник: domrf-lk.ru
ОПРЕДЕЛИТЬ ПРИНАДЛЕЖИТ ЛИ ТОЧКА С КООРДИНАТАМИ X Y ЗАШТРИХОВАННОЙ ЧАСТИ ПЛОСКОСТИ PYTHON
Определение принадлежности точки к заданной области на плоскости – одна из наиболее распространенных задач в программировании. В Python для решения этой задачи можно использовать математическую библиотеку NumPy и ее функцию numpy.point_inside_polygon() .
Для начала необходимо определить координаты всех вершин многоугольника, образующего заданную область. Это можно сделать вручную, либо задавать программно, в зависимости от объема и структуры исходных данных. Например, для многоугольника, ограниченного точками (0,0), (0,1), (1,1), (1,0), зададим координаты вершин следующим образом:
polygon = [(0, 0), (0, 1), (1, 1), (1, 0)]
Далее, для определения принадлежности заданной точки к заданной области, необходимо вызвать функцию numpy.point_inside_polygon() и передать ей координаты точки и координаты вершин многоугольника, используя ранее созданные переменные:
from numpy import point_inside_polygon
point = (0.5, 0.5)
is_inside = point_inside_polygon(point, polygon)
В данном примере определяется принадлежность точки (0.5, 0.5) заданному многоугольнику. Результат работы функции сохраняется в переменной is_inside , которая примет значение True , если точка принадлежит заданной области, и False , если нет.

Программирование на С++. Урок 10. Попадает ли точка в заштрихованную область
Попадание точки в заданную область. Два сектора. Уроки программирования на С++.
Exact Areas and Definite Integral with Python
Стать программистом в 40+? О сложностях в обучении и устройстве на работу. Демотивирующее видео.
15 Фишек с СЛОВАРЯМИ Python, которые сделают код лучше
33 Задача: Принадлежит ли точка кругу с центром в начале координат?
Программирование на С++. Урок 11. Попадает ли точка в заштрихованную область 2.

Новые материалы:
- Python c или java
- Python pywin32 документация
- Import this python какое первое слово в последней строке выведет эта программа
- Django составной первичный ключ
- Курсы hexlet python скачать
- Переполнение стека python
- Как отправить фото с подписью в телеграмм python
- Как посчитать количество элементов в списке python
- Asdict в python
- Как убрать n python при чтении из файла
- Opencv в python часть 2
- Игры написанные на python
- Курс искусственный интеллект python
- Асинхронные запросы python
Источник: pygame.ru
Уроки 70 — 74
Условный оператор. Сложные условия
§57. Ветвления
1. Покажите, что приведённая программа не всегда верно определяет максимальное из трёх чисел, записанных в переменные а, b и с:

Приведите контрпример, т. е. значения переменных, при котором в переменной М будет получен неверный ответ. Как нужно доработать программу, чтобы она всегда работала правильно?
2. Напишите программу, которая выбирает максимальное и минимальное из пяти введённых чисел.
3. Напишите программу, которая определяет, верно ли, что введённое число трёхзначное.
4. Напишите программу, которая вводит номер месяца и выводит название времени года. Оператор выбора использовать не разрешается. При вводе неверного номера месяца должно быть выведено сообщение об ошибке.
5. Решите предыдущую задачу с помощью оператора выбора.
6. Напишите программу, которая вводит с клавиатуры номер месяца и определяет, сколько дней в этом месяце. При вводе неверного номера месяца должно быть выведено сообщение об ошибке.
7. Напишите программу, которая вводит с клавиатуры номер месяца и день и определяет, сколько дней осталось до Нового года. При вводе неверных данных должно быть выведено сообщение об ошибке.
8. Напишите программу, которая вводит возраст человека (целое число, не превышающее 120) и выводит этот возраст со словом «год», «года» или «лет». Например: «21 год», «22 года», «25 лет».
9. Напишите программу, которая вводит целое число, не превышающее 100, и выводит его прописью, например: 21 → «двадцать один».
10. Напишите программу, которая вводит координаты точки на плоскости и определяет, попала ли эта точка в заштрихованную область.

11. Напишите два варианта программы, которая вводит координаты точки на плоскости и определяет, попала ли эта точка в заштрихованную область. Один вариант программы должен использовать сложные условия, второй — обходиться без них.
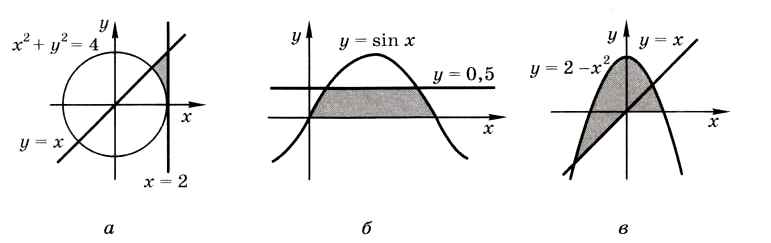
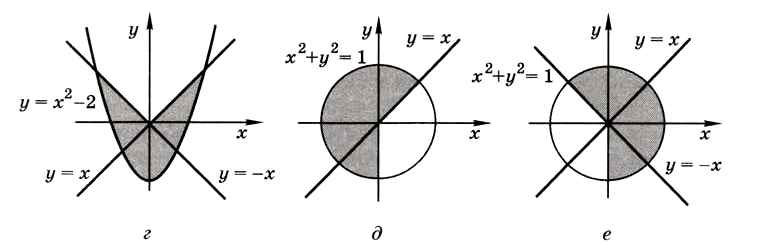
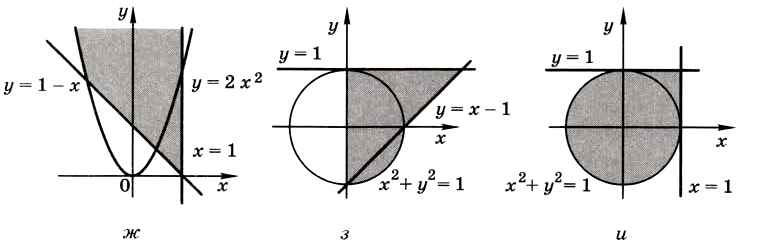

Следующая страница §57. Ветвления

Cкачать материалы урока
Источник: xn—-7sbbfb7a7aej.xn--p1ai