Напишите программу, которая определяет, попала ли точка с заданными координатами в заштрихованную область. Формат ввода Входная строка содержит два вещественных числа – координаты точки на плоскости (сначала x -координата, затем – y -координата). Формат вывода Программа должна вывести слово ‘YES’, если точка попала в заштрихованную область, и слово ‘NO’, если не попала. Примеры: Ввод -0.5 и 0.5 вывод YES Ввод -2 и 2 вывод NO Ввод 0.5 и -0.5 вывод NO Pascal abc.net
Источник: cwetochki.ru
Как определить лежит ли точка на прямой
Сегодня мы рассмотрим еще одну типовую задачу из серии геометрические алгоритмы. Напишем функцию, которая будет проверять принадлежность произвольной точки отрезку, заданному координатами своего начала и конца.
Для реализации операций сравнения над вещественными данными напишем еще две функции: функцию EqPoint(), которая ,будет проверять, совпадают ли две точки на плоскости и функцию RealMoreEq() , которую будем использовать для проверки отношения «>=» (больше или равно). Причина ввода специальных функций нам уже известна.
Попадание точки в заданную область. Два сектора. Уроки программирования на С++.
Задача. Проверить, принадлежит ли точка отрезку.
Пусть точки — начальная и конечные точки отрезка. — произвольная точка на плоскости.
Вектор с началом в точке и концом в точке будет иметь координаты (x2-x1, y2-y1).
Если P(x, y) – произвольная точка, то координаты вектора равны: (x-x1, y – y1).
Точка Р будет принадлежать отрезку если:
- Векторы в и коллинеарны (равно нулю их векторное произведение):
, т.е. (x-x1)(y2-y1)-(y-y1)(x2-x1) = 0 - Абсцисса точки P удовлетворяет условию: или . Иначе точка будет находиться на прямой левее или правее отрезка.
Результаты выполнения программы.
Введите координаты точек: x1, y1, x2, y2, x,y
0.5 1 2.5 2.8 1.203 1.633
Да.
Результаты тестирования в программе GeoGebra:
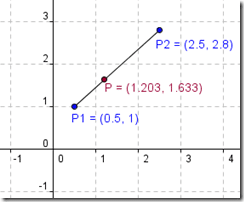
Сегодня мы написали функцию AtOtres() , которая проверяет принадлежность произвольной точки отрезку, заданному своими координатами.
Ввели еще две функции: EqPoint() и RealMoreEq() для реализации операций сравнения над вещественными данными. Первая проверяет, совпадают ли две точки на плоскости, вторая — используется для проверки отношения «>=».
На следующем уроке, на основе ранее написанных процедур, напишем процедуру определения координат точки пересечения двух отрезков.
На этом я с вами прощаюсь. До встречи на следующем уроке.
Ответ
Проверено экспертом

Точка лежит на прямой, если её координаты удовлетворяют уравнению прямой, т.е. при их подстановке вместо неизвестных (х и у) получается верное числовое равенство.
33 Задача: Принадлежит ли точка кругу с центром в начале координат?
а(-5;3)
-5-4*3+7=0 ?
-5-12+7≠0
-10≠0 => точка А не принадлежит прямой
в(9;4)
9-4*4+7=0 ?
9-16+7=0
0=0 => В лежит на прямой, заданной уравнением х-4у+7=0
Как в canvas определить лежит ли точка на прямой. Уточню — прямая толстая, то есть по сути это наклонный прямоугольник.
Пробовал по формуле взятой из этого вопроса и с небольшой погрешностью.
В случае с наклонными линиями все работает. Но если линия горизонтальная или вертикальная, то вычисление по данной формуле равно Infinity . А если прямых несколько, то соответственно не определить, на которой из них располагается точка
Подскажите пожалуйста алгоритм.
1 ответ 1
Проще всего воспользоваться псевдоскалярным произведением.
Если линия задана двумя точками A(x1, y1) и B(x2, y2) , и третья точка C(x, y) , то надо подсчитать величину
Эта величина равна удвоенной (ориентированной) площади треугольника, составленного тремя точками, и равна нулю если три точки лежат на одной прямой.
Работает, очевидно, вне зависимости от вертикальности/горизонтальности прямых.
Вы можете вычислять расстояние от точки C до прямой AB , поделив на длину отрезка AB . Величины dx1 , dy1 и |AB| = Math.Sqrt(dx1 * dx1 + dy1 * dy1) можно подсчитать заранее.
Если ваша прямая имеет заданную толщину d , можно сравнивать с ней:
Нет связанных сообщений
Источник: technicspace.ru
Лабораторная работа №2: Попадание точки в заданную область

- 1. Область заштрихована и ограничена линиями контура. Описать математически систему неравенств, обеспечивающую попадание произвольной точки в заштрихованную область;
- 2. Программу оформить в виде подприбора (структура подприбора показана на рисунке 24):
- — Входы — координата X, координата Y;
- — Выходы — результат логического выражения и строковый ответ «точка попадает в область» / «точка не попадает в область»;
Содержание отчета
- 1. Название работы, номер варианта индивидуального задания.
- 2. Фамилия, имя, отчество и номер группы студента.
- 3. Рисунок в том виде, как он приведен в варианте задания.
- 4. Уравнения всех линий, ограничивающих заштрихованную область.
- 5. Система неравенств координат всех точек заштрихованной области.
- 6. Блок — диаграмма программы.
Варианты индивидуального задания






Лабораторная работа №3: Условные операторы
Задание
Разработать виртуальный прибор для решения задачи, согласно заданному варианту индивидуального задания.
Содержание отчета
- 1. Название работы, номер варианта индивидуального задания.
- 2. Фамилия, имя, отчество и номер группы студента.
- 3. Текст задания индивидуального варианта.
- 4. Блок — диаграмма программы.
- 5. Блок — схема программы.
Варианты индивидуальных заданий
Дано трехзначное число. Определить:
- а) верно ли, что все его цифры одинаковые;
- б) есть ли среди его цифр одинаковые.
Дано двухзначное число. Определить:
- а) входит ли в него цифра 5;
- б) входит ли в него цифра а .
Ввести с клавиатуры координаты точек А|(х|,у1) , А,(х2,у2) , А3(л^,у3). Определить, можно ли через точку А3 провести прямую, перпендикулярную прямой, проходящую через точки Д и А2. Ответ вывести в виде сообщения.
Написать программу, которая при вводе числа в диапазоне от 1 до 99 добавляет к нему слово «копейка» в правильной форме. Например: «1 копейка», «5 копеек», «42 копейки».
Ввести с клавиатуры координаты точки А (х, у). Определить, попадает ли точка А в область, ограниченной окружностью 1 = у 2 + (х-1) 2 . Ответ вывести в виде сообщения.
Определить, является ли шестизначное число «счастливым» (сумма первых трех цифр равна сумме последних трех цифр).
Дано целое число от 1 до 365. Определить, какой день недели выпадает на это число, если 1 января — понедельник.
Траектория снаряда, вылетающего из орудия под углом а с начальной скоростью v0 , определяется уравнениями x = v0Zcosa у = vot sin а — 98г / 2. Определить попадет ли снаряд в цель размером h, находящуюся в плоскости его полета на расстоянии R и высоте Н .
Дано трехзначное число. Определить:
- а) является ли сумма его цифр двухзначным числом;
- б) является ли произведение его цифр трехзначным числом.
Дано трехзначное число. Определить:
- а) является ли произведение его цифр больше числа b;
- б) кратна ли сумма его цифр трем.
Даны вещественные числа а , b , с , а^О . Решить уравнение ах 2 +Ьх + с = 0. Учесть возможность равенства корней.
Ввести с клавиатуры координаты точки А(х,у). Определить, лежит ли точка А в области, ограниченной параболой у = 2 — х 2 и прямой у = -2. Ответ вывести в виде сообщения.
Дано двухзначное число. Определить:
- а) входят ли в него цифры 3 и 7;
- б) входят ли в него цифры (4 и 8) или цифра 9.
Рейтинг бакалавра заочного отделения при поступлении в магистратуру определяется средним баллом по диплому, умноженным на коэффициент стажа работы по специальности, который равен: нет стажа — 1, меньше 2 лет — 13, от 2 до 5 лет — 16. Составить программу расчета рейтинга при заданном среднем балле диплома (от 3 до 5) и вывести сообщение о приеме в магистратуру при проходном балле 45.
Даны целочисленные координаты трех вершин прямоугольника, стороны которого параллельны координатным осям. Определить координаты четвертой вершины.
Дано четырехзначное число. Определить:
- а) равна ли сумма двух первых его цифр сумме двух последних;
- б) кратна ли 7 сумма его цифр.
Дано четырехзначное число. Определить:
- а) кратно ли произведение его цифр трем;
- б) кратно ли числу а произведение его цифр.
Даны вещественные положительные числа а , b , с , d . Выяснить, можно ли прямоугольник со сторонами а , b поместить в прямоугольник со сторонами с , d так, чтобы стороны одного прямоугольника были параллельны или перпендикулярны сторонам другого прямоугольника.
Даны вещественные положительные числа а, b, с , х, у. Выяснить, пройдет ли кирпич размером axbxc в отверстие размером хху при параллельном или перпендикулярном расположении ребер кирпича сторонам отверстия.
Написать программу, которая при вводе числа в диапазоне от 1 до 20 добавляет к нему слово «гривна» в правильной форме. Например, «1 гривна», «2 гривны», «5 гривен».
Ввести число от 1 до 31. Определить ближайшую (следующую) дату полнолуния или новолуния (лунных месяц содержит 28 дней), если последнее полнолуние было 27 августа.
Определить проводник с максимальным сопротивлением, если даны три проводника с удельным сопротивлением , г2, г3 и площадью сечения s2, s3.
Дано натуральное четырехзначное число. Выяснить, является ли оно палиндромом (читается одинаково слева направо и справа налево).
Определить максимальный предельный заряд и минимальный
потенциал ^min для трех шаров с диаметром rt, г2, г3. Напряженность поля, при которой начинается ударная ионизация, равна Е = 3 МВ/м р
Написать программу для сравнения радиусов окружностей, которые описывают протон и альфа-частица, если влетают в однородное магнитное поле перпендикулярно линиям индукции:
- а) при одинаковой скорости;
- б) при одинаковой энергии.
Вывести сообщение. Заряд альфа-частицы в 2 раза больше заряда протона, а масса в 4 раза больше.
Локатор может быть ориентирован на одну из сторон света («С» -север, «Ю» — юг, «3» — запад, «В» — восток) и может принимать команды: «1» — поворот направо (90°), «-1» — поворот налево (-90°), «2» — поворот в обратную сторону (180°). Исходная ориентация локатора «С». Определить ориентацию локатора после выполнения последовательности вводимых команд N1, N2.
Ввести длину волны и определить попадает ли она в рабочий диапазон длин волн приемника, если емкость конденсатора в его колебательном контуре плавно изменяется от 50 до 500 пФ, а индуктивность катушки постоянна и равна 20 мкГн.
Дано трехзначное число а . Определить:
- а) является ли произведение его цифр меньше числа я ;
- б) кратна ли 5 сумма его цифр.
Написать программу, определяющую условие, когда сдвиг фаз между током и напряжением при последовательном соединении сопротивления, емкости и конденсатора будет положительным, отрицательным и равным нулю.
Ввести с клавиатуры координаты точки А(лру,) . Определить, попадает
ли точка А в область, ограниченной линиями у = х, у = -х иу = 1. Ответ вывести в виде сообщения.
Источник: ozlib.com