Бесконечная числовая последовательность задана с помощью формулы ее k-го элемента: Ak = k!*2^k, где k = 1, 2, 3. Найти сумму N первых элементов этой последовательности по модулю M. Первая строка входного потока содержит два целых числа N — количество членов последовательности (1 ≤ N ≤ 10^4) и M — модуль (2 ≤ M ≤ 10^9). В выходной поток вывести сумму N первых элементов заданной последовательности по модулю M. Пример входного потока: 5 10 Пример выходного потока: 2
#include #include using namespace std; long fact (long v) < int z=1; for (long i=1;i<=v;i++) < z*=i; >return z; > int main() < long n,m,elem,sum=0; cin >> n >> m; for (long i=1;i <=n;i++) < elem=fact(i)*pow(2,i); sum+=elem; >cout
Проходит только 1 тест. Подскажите, пожалуйста, что делать? https://acmp.ru/index.asp?main=taskпочитать сумму, а потом взять от нее модуль» не сработает — числа слишком большие, в long не влезут.
8 янв 2019 в 1:02
Вместо этого нужно применять модуль чаще. Скажем, после каждого умножения ( *= ) при вычислении факториала делать z %= m; . Аналогично после умножения при возведении в степень, и аналогично после каждого сложения при вычислении суммы. За счет этого не придется работать с огромными числами, а ответ не поменяется. Если после этого размера переменных все равно не хватит, попробуйте long long вместо long .
Алгебра 9 класс (Урок№31 — Последовательности.)
8 янв 2019 в 1:02
8 янв 2019 в 1:14
Источник: ru.stackoverflow.com
Написать программу определения заданной характеристики последовательности чисел c1 c2 cn
Вычислить значение суммы
S = 1/1! + 1/2! + . + 1/k!
Написать программу определения количества шестизначных ‘счастливых’ билетов, у которых сумма первых 3 десятичных цифр равна сумме 3 последних десятичных цифр.
Написать программу определения количества 2*N -значных билетов, у которых сумма первых N десятичных цифр равна сумме N последних десятичных цифр; при этом N -произвольное натуральное число.
Фишка может двигаться по полю длины N только вперед. Длина хода фишки не более K. Найти число различных путей, по которым фишка может пройти поле от начала до конца.
Покупатель имеет купюры достоинством A(1), . A(n), а продавец — B(1), .. ,B(m). Необходимо найти максимальную стоимость товара Р, которую покупатель не может купить, потому что нет возможности точно рассчитаться за этот товар с продавцом, хотя денег на покупку этого товара достаточно.
Задан массив М [1:N] натуральных чисел, упорядоченный по неубыванию, т.е.: M[1]
Найти первое натуральное число, не представимое суммой никаких элементов этого массива, при этом сумма может состоять и из одного слагаемого, но каждый элемент массива может входить в нее только один раз.
У покупателя есть n монет достоинством H(1). H(n). У продавца есть m монет достоинством B(1). B(l). Может ли купить покупатель вещь стоимости S так, чтобы у продавца нашлась точная сдача (если она необходима).
Как найти предел числовой последовательности с общим членом ((n+1)(n+2)…(2n))^(1/n)/n?
Задан массив М [1:N] натуральных чисел, упорядоченный по неубыванию, т.е.: M[1]
Написать алгоритм выплаты заданной суммы S минимальным количеством купюp достоинством M(1), . M(N).
По матрице A(N,N) построить матрицу B(N,N). Элемент B(I,J) равен максимальному из элементов матрицы А принадлежащем части, ограниченной справа диагоналями, проходящими через A(I,J).
Вводится матрица a(m,n) из 0 и 1. Найти в ней квадратную подматрицу из одних единиц максимального размера.
Вводится матрица a(m,n) из 0 и 1. Найти в ней прямоугольную подматрицу из одних единиц максимального размера (т.е. с максимальным произведением высоты на длину).
Переформулировка задачи 11.
Фермер хочет построить на своей земле как можно больший по площади сарай. Но на его участке есть деревья и хозяйственные постройки, которые он не хочет никуда переносить. Для простоты представим ферму сеткой размера MxN. Каждое из деревьев и построек размещается в одном или нескольких узлах сетки. Прямоугольный сарай не должен ни с чем соприкасаться (т.е. в соседних с ним узлах сетки не может ничего быть).
Найти максимально возможную площадь сарая и где он может размещаться.
Дан массив A[N,M]. Необходимо найти максимальную сумму элементов прямоугольного подмассива по всем возможным прямоугольным подмассивам.
Задана матрица натуральных чисел A(n,m). За каждый проход через клетку (i,j) взымается штраф A(i,j). Необходимо минимизировать штраф и
а) Пройти из какой-либо клетки 1-ой строки в n-ую строчку, при этом из текущей клетки можно перейти
1) в любую из 3-х соседних, стоящих в стpоке с номеpом на 1-цу большем;
2) в любую из 8 соседних клеток;
б) Реализовать пункт a) для перехода из клетки (1,1) в (n,m).
Дан выпуклый n-угольник, n=>3, своим обходом по контуру. Разбить его на треугольники (n-3)-мя диагоналями, непересекающимися кроме как по концам, таким образом чтобы
а) Cумма их длин была минимальной;
б) Максимальная из диагоналей имела наименьшую длину.
Задано число А и два вектора b[1..n] и c[1..n].
Найти множество I, являющееся подмножеством множества , такое, что
является максимальной из всех
Пусть x=(a 1 ,a 2 . a m ) и y=(b 1 ,b 2 . b n ) — две заданных строки символов.
Определим d(x,y) как минимальное число вставок, удалений и замен символа, которое необходимо для преобразования x в y.
Для заданных x и y найти d(x,y).
Вводится три неотрицательных числа d, i, c и две строки X и Y. Найти преобразование строки X в Y минимальной стоимости. Допустимы следующие три операции:
удалить любой символ из X (стоимость операции d);
вставить любой символ в X (стоимость операции i);
заменить символ в X на произвольный (стоимость операции e).
Даны две строки x и y. Строка x состоит из нулей и единиц, строка y из символов A и B. Можно ли строку x преобразовать в строку y по следующему правилу: цифра 0 преобразуется в непустую последовательность букв A, а цифра 1 — либо в непустую последовательность букв A, либо в непустую последовательность букв B?
Пусть известно, что для перемножения матрицы размера n*m на матрицу размера m*k требуется n*m*k операций. Необходимо определить, какое минимальное число операций потребуется для перемножения n матриц А 1 . А n , заданных своими размерами n(i)*m(i). При этом можно перемножать любые две рядом стоящие матрицы, в результате чего получается матрица нужного размера.
n(i) — число строк в матрице A i
m(i) — число столбцов в матрице A i
а) Из последовательности, состоящей из N чисел, вычеркнуть минимальное количество элементов так, чтобы оставшиеся образовали строго возрастающую последовательность.
б) Из заданной числовой последовательности A[1..N] вычеркнуть минимальное число элементов так, чтобы в оставшейся подпоследовательности каждый последующий элемент был больше предыдущего кроме, быть может, одной пары соседних элементов ( одного «разрыва» возрастающей подпоследовательности).
Искомая подпоследовательность (1,2,3,2,3,4,6)
б) Из заданной числовой последовательности A[1..N] вычеркнуть минимальное число элементов так, чтобы в оставшейся подпоследовательности каждый последующий элемент был больше предыдущего кроме, быть может, m пар соседних элементов ( возрастающая подпоследовательность с m «разрывами»).
В заданной последовательности целых чисел найти максимально длинную подпоследовательность чисел такую, что каждый последующий элемент подпоследовательности делился нацело на предыдущий.
Возвести число А в натуральную степень n за как можно меньшее количество умножений.
Заданы z и y — две последовательности. Можно ли получить
последовательность z вычеркиванием элементов из y.
Найти максимальную по длине последовательность z, полученную
вычеркиванием элементов как из x, так и из y.
Пусть x и y — две бинарных последовательности (т.е. элементы последовательностей — нули и единицы); x и y можно рассматривать как запись в двоичной форме некоторых двух натуральных чисел.
Найти максимальное число z, двоичную запись которого можно получить вычеркиванием цифр как из x, так и из y. Ответ выдать в виде бинарной последовательности.
Источник: algolist.ru
Дана последовательность мнемокодов, которую необходимо преобразовать в машинные коды, занести в озу эвм, выполнить в режиме шаг и зафиксировать Изменение состояний программно-доступных объектов эвм.
3.1.4 В тетради заполните столбец Действие для каждой используемой команды программы.
3.1.5 Нарисуйте алгоритм работы программы.
3.2 Запишите в ОЗУ программу, состоящую из 5 команд (из своего варианта). Команды разместите в ячейках памяти.
3.2.1 При необходимости установить начальное значение в устройство ввода IR.
3.2.2 Определить те программно-доступные объекты ЭВМ, которые будут изменяться при выполнении этих команд.
3.2.3 Выполнить в режиме Шаг введенную последовательность команд, фиксируя изменения значений объектов, определенных в п. 4, в таблице 4. Содержание регистров, по примеру:
Таблица 4 Содержание регистров для задачи 2
| PC | Acc |
3.2.4 Если в программе образуется цикл, необходимо просмотреть не более двух повторений каждой команды, входящей в тело цикла.
Таблица 5 Задание для выполнения
3.2.5 Напишите машинные коды команд, соответствующие варианту задания.
3.3 Программирование разветвляющегося процесса. Разработать программу вычисления и вывода значения функции для вводимого из IR значения аргумента x:

Варианты заданий приведены ниже в таблице:
Таблица 6 Выбор значений параметров i, j, a
| № | i | j | a | № | i | j | a | № | i | j | a | № | i | j | a | № | i | j | a |
Таблица 7Выбор функции
| k | fk(x) | k | fk(x) | k | fk(x) | k | fk(x) | k | fk(x) |
 |
 |
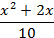 |
 |
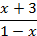 |
|||||
 |
 |
 |
 |
 |
· Пример выполнения задания – программа для вычисления значения функции:

. С устройства ввода IR вводится значение x, результат выводится на OR.
· Блок-схема выполнения задания на рисунке Рисунок 1 Блок-схема алгоритма задачи (см. ниже):

Рисунок 1 Блок-схема алгоритма задачи
· Реализация программы указана в таблице Таблица 8 Пример выполнения задания по блок-схеме
Таблица 9 Пример выполнения задания по блок-схеме
| Мнемокод | Примечание |
| 00) in 01) wr 30 02) sub #16 03) js m1 04) rd 30 05) sub #11 06) wr 31 07) mul 31 08) sub #125 09) jmp m1 010) m1: rd 30 011) mul 30 012) wr 31 013) rd 30 014) mul #72 015) add 31 016) adi 106400 017) divi 100168 018) m2: out 019) hlt | Ввод х Размещение х в ОЗУ Сравнение с границей – (х-16) Переход по отрицательной разности Вычисления по первой формуле Переход на вывод результата Вычисления по второй формуле Вывод результата Стоп |
3.4 Дополнительное задание: Программирование цикла с переадресацией. Требуется разработать программу для определения заданной последовательности чисел C1, C2, …,Cn. Варианты заданий представлены ниже в таблице 10 Задание на тему циклы:
Таблица 10 Задание на тему циклы
| № варианта | Характеристика последовательности чисел C1, C2, …,Cn |
| Количество чисел, имеющих чётный индекс | |
| Номер минимального числа | |
| Произведение всех чисел | |
| Минимальное положительное число | |
| Количество чисел, равных C1 | |
| Количество отрицательных чисел | |
| Максимальное положительное число | |
| Номер максимального числа | |
| Количество чисел, меньших C1 | |
| Разность сумм элементов массива, имеющих чётные и нечётные индексы |
3.4.1 Пример выполнения задания – программа вычисления суммы элементов массива чиселC1, C2, …,Cn. Исходными данными являются n – количество элементов массива, массив чисел C1, C2, …,Cn. Должно выполняться условие n>1, так как алгоритм предусматривает хотя бы одно суммирование. Суммируемые числа записаны в ОЗУ подряд, т.е. в ячейки памяти с последовательными адресами. Результатом является сумма S.
3.4.1.1 Составим программу для вычисления суммы 10 чисел, элементы массива расположены в ячейках ОЗУ по адресам 040, 041,…, 049.
3.4.1.2 Программу распределим в памяти, начиная с адреса 000.
3.4.1.3 Промежуточные переменные: Ai – в ячейке с адресом 030, k – по адресу 031, S – по адресу 032.

Рисунок 2 Блок-схема решения задачи на тему Циклы
3.4.2 Реализация программы указана в таблице 11 Решение задачи на тему Циклы
Таблица 12 Решение задачи на тему Циклы
4 Содержание отчёта:
4.1.1 Формулировка варианта задания
4.1.2 Граф-схема алгоритма решения задачи
4.1.3 Распределение памяти (размещение в ОЗУ переменных, программы и констант)
4.1.4 Программа с описанием действий
4.1.5 Последовательность состояний регистров ЭВМ при выполнении программы в режиме Шаг для одного значения аргумента (для задания 3.3).
4.1.6 Значения исходных данных и результата выполнения программы (для задания 3.4 – для нескольких значений аргументов, выбранных самостоятельно).
5 Контрольные вопросы:
5.1 Что такое система команд ЭВМ?
5.2 Способ представления данных в модели.
5.3 Способы адресации. Рассмотреть на примере.
5.4 Какие классы команд были использованы в задании?
5.5 Какие действия выполняют команды передачи управления?
5.6 Как организовать безусловный переход в программе?
5.7 Как организуется цикл?
5.8 Что такое параметр цикла?
5.9 Как поведёт себя программа из примера к третьему заданию, если в ней будет отсутствовать команда wr 31 по адресу 014?
Источник: infopedia.su