Машина Тьюринга состоит из бесконечной в обе стороны ленты, разбитой на ячейки, и рабочей головки. Она работает в дискретные моменты времени: t0, t1, …, tn, … В каждый момент во всякой ячейке ленты может быть записана одна из букв некоторого конечного внешнего алфавита A = < a0, a1, … ak-1>, а головка может находиться в одном из конечного числа внутренних состояний
Q = 0,q1,…qr-1>- внутренний алфавит. Символ a0является «пустым» (будем обозначать его L) и что все клетки ленты заполнены этим символом.
В каждый момент времени рабочая головка обозревает одну ячейку ленты и выполняет следующие действия:
1) заменяет символ в обозреваемой ячейке новым (возможно, прежним);
2) переходит в новое состояние (возможно, в прежнее);
3) сдвигается на одну ячейку (вправо R или влево L ) либо остается на месте H.
Совокупность команд будем называть программой машины Тьюринга.
Среди состояний машины (головки) выделено одно, называемое заключительным (впредь мы будем считать, что это состояние q0).
Как запрограммировать на машине Тьюринга сложение? Душкин объяснит
Под конфигурацией машины Тьюринга мы понимаем распределение букв алфавита А по ячейкам ленты, состояние головки и обозреваемую ячейку. Работа машины Тьюринга по программе состоит в смене конфигураций. Конфигурацию в момент времени ti будем обозначать K ti. Если эта конфигурация не является заключительной, то машина в соответствии со следующей командой переходит в конфигурацию K ti+1.
Если нужно решить некоторую задачу на машине Тьюринга, исходным данным задачи сопоставляется начальная конфигурация K t0, а ответ задачи определяется заключительной конфигурацией, в которую программа машины переводит конфигурацию K t0.
1. Пусть требуется добавить 1 к натуральному числу n, представленному на ленте машины Тьюринга в двоичной системе счисления, то есть в алфавите .
Решение: внешний алфавит машины будет следующим: < L, 0, 1 >.
Будем считать начальной следующую конфигурацию: Lq1s1…spL. Для того, чтобы прибавить 1 к двоичному числу n сначала необходимо «отогнать» головку машины вправо и установить ее под последней (самой младшей) цифрой двоичного числа. Если последняя цифра числа есть 0, то достаточно заменить 0 на 1 и завершить процесс, то есть перевести головку (машину) в заключительное состояние q0.
Если же последняя цифра числа есть 1, то необходимо заменить ее на 0, а головку сдвинуть влево, чтобы «увидеть» следующий разряд двоичного числа. Если окажется, что этот разряд содержит 0, то заменить 0 на 1 и опять-таки перевести головку (машину) в заключительное состояние q0. Если же этот разряд содержит 1, необходимо заменить ее на 0 и опять сдвинуть головку влево. И так далее, до тех пор, пока либо не встретится разряд, содержащий 0, либо головка дойдет до первого слева пустого символа L. В любом из этих случаев 0 или L следует заменить на 1 и перевести головку (машину) в заключительное состояние q0.
Программа машины, прибавляющей 1 к двоичному числу, имеет вид:
Конструирование машины Тьюринга
| q11 ®q11R q10 ®q10R q1L ®q2LL q20 ®q31H q21 ®q20L | q2L ®q01H q31 ®q31L q30 ®q30L q3L ®q0LR. |
2. Пусть требуется перевести запись натурального числа n, изображенного в виде последовательности n «палочек» (|) n ³ 1, в двоичную запись в алфавите . Т.е. конфигурация Lq1…|L должна быть преобразована в Lq0s1s2…sp L, где s1s2…sp — двоичная запись n.
Решение: в качестве внешнего алфавита машины берем алфавит:< L, |, 0,1 >.
Опишем алгоритм решения задачи в словесной форме:
1. «Отогнать» головку машины влево до первого пустого символа, заменить этот символ нулем (0).
2. «Отогнать» головку машины вправо до последней черточки, заменить ее пустым символом. Запомнить, что 1 из унарного представления числа n вычтена.
3. Установить головку под младшим разрядом формируемого двоичного числа и прибавить к двоичному числу 1 (так как мы делали это при построении предыдущей машины). Запомнить, что 1 к двоичному числу прибавлена.
4. Пункты 2 и 3 повторять до тех пор, пока не исчерпается исходное число, то есть на ленте не останется «палочек».
5. Головку отогнать в крайнюю левую позицию полученного двоичного числа и остановить машину.
Программа работы машины имеет вид:
| q1| ®q1|L q1L®q20R q2| ®q2|R q2L ®q3LL q3| ®q4 LL q4 | ®q4|L q40 ®q51R q41®q40L | q4 L®q51R q51 ®q51R q50 ®q50R q5| ®q2|H q5 L ®q6 LL q61 ®q61L q60 ®q60L q6 L ®q0LR |
3. Составьте программу машины Тьюринга, подсчитывающую число вхождений символа a в слово Р в алфавите .
Решение: пусть начальная конфигурация машины имеет вид q1P.
Надо перевести ее в конфигурацию q0n*P, где n – двоичное число, выражающее число вхождений символа a в слово Р в алфавите < a, b, c >.
Опишем алгоритм решения задачи в словесной форме:
1. Слева от слова Р приписываем символы 0 и *.
2. Находим в слове Р вхождение символа a, заменяем его на a ’ , запоминаем, перемещаем головку влево, прибавляем 1 к двоичному числу n («счетчику»).
3. Повторяем п. 2 до тех пор, пока не пройдем все слово P.
4. Убираем все штрихи в слове Р.
5. Устанавливаем головку машины под крайней левой цифрой двоичного числа n и останавливаем машину.
Программа работы машины имеет вид:
| q1a ® q2aL q1b ® q2bL q1c ® q2cL q2L ® q3*L q3L ® q40R q40 ® q40R q41 ® q41R | q4*® q5*R q5b® 5bR q5c® q5cR q5a ’ ®q5a ’ R q5a® 6a ’ H q6b® q6bL q6c ® q6cL | q6a ’ ® q6a ’ L q6* ® q6*L q60 ® q41R q61 ® q60L q6L ® q41L q5L® q7LL q7a ® q7aL | q7b ® q7bL q7c ® q7cL q7a ’ ® q7aL q7* ® q7*L q70 ® q70L q71 ® q71L q7L ® q0LR |
Задания для самостоятельного выполнения
Источник: studopedia.su
Алгоритмы: машины Тьюринга
Машину Тьюринга  будем называть распознающей, если для некоторого алфавита
будем называть распознающей, если для некоторого алфавита  и каждого входа
и каждого входа 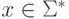 , на котором
, на котором  останавливается, ее результат
останавливается, ее результат  , т.е.
, т.е.  вычисляет некоторую двузначную функцию (возможно частичную) на словах из
вычисляет некоторую двузначную функцию (возможно частичную) на словах из 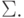
Лемма 9.5. Пусть  — распознающая м.Т ., м.Т .
— распознающая м.Т ., м.Т .  вычисляет функцию f(x) , а м.Т .
вычисляет функцию f(x) , а м.Т . 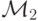 — функцию g(x) . Тогда существует м.Т .
— функцию g(x) . Тогда существует м.Т . 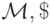 вычисляющая функцию
вычисляющая функцию
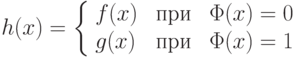 . Выбор между f и g происходит по следующим командам :
. Выбор между f и g происходит по следующим командам :
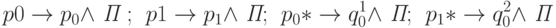
Кроме того, обеспечим переход в новое заключительное состояние:
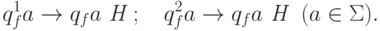
Таким образом, мы реализовали в терминах машин Тьюринга обычный в языках программирования оператор ветвления :
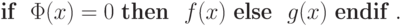
Повторение (цикл)
Используя конструкцию для ветвления легко реализовать в терминах машин Тьюринга и оператор цикла .
Лемма 9.6. Пусть  — распознающая м.Т ., а м.Т .
— распознающая м.Т ., а м.Т .  вычисляет функцию f(x) . Тогда существует м.Т .
вычисляет функцию f(x) . Тогда существует м.Т . 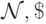 которая вычисляет функцию, задаваемую выражением:
которая вычисляет функцию, задаваемую выражением:
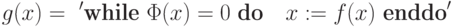
Доказательство. Действительно, пусть м.Т . 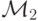 — вычисляет тождественную функцию g(x)=x . Построим по м.Т .
— вычисляет тождественную функцию g(x)=x . Построим по м.Т . 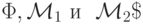 м.Т .
м.Т . 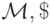 реализующую ветвление как в лемме 9.5. Тогда искомая м.Т .
реализующую ветвление как в лемме 9.5. Тогда искомая м.Т . 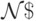 получается из
получается из 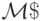 заменой команд
заменой команд 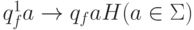 на соответствующие команды
на соответствующие команды  , обеспечивающие зацикливание.
, обеспечивающие зацикливание.
Реализованные выше операции над машинами Тьюринга и вычислимыми функциями позволяют получать программы новых м.Т ., используя обычные конструкции языка программирования «высокого» уровня: последовательную и параллельную композицию , ветвление и цикл . Пусть 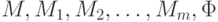
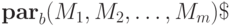 (здесь b — это символ, разделяющий аргументы и результаты этих машин), ветвление —
(здесь b — это символ, разделяющий аргументы и результаты этих машин), ветвление —

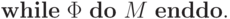
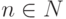
Пример 9.4. Рассмотрим в качестве примера задачу перевода чисел из унарной системы счисления в двоичную. Пусть f ub (| n ) = n(2) для всех , где n(2) — двоичная запись числа n .
Пусть M1 — м.Т ., которая начальную конфигурацию q0 ,| n переводит в конфигурацию q1 ,0*| n ; M2 — м.Т ., которая прибавляет 1 к двоичному числу-аргументу (см. пример ref); M3 — м.Т ., которая вычитает 1 из унарного числа; 
 ); M4 — м.Т ., которая стирает * в аргументе вида x* и останавливается. Реализация каждой из указанных м.Т . очевидна. Теперь требуемая м.Т . Mub , вычисляющая f ub , получается как
); M4 — м.Т ., которая стирает * в аргументе вида x* и останавливается. Реализация каждой из указанных м.Т . очевидна. Теперь требуемая м.Т . Mub , вычисляющая f ub , получается как
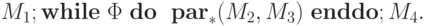
Действительно, после работы M1 получаем конфигурацию q10*| n . Предположим теперь по индукции, что после i (i цикла while получается конфигурация q1 i(2)*| n-i . Тогда на (i+1) -ой итерации цикла после параллельного применения M2 к i(2) и M3 к | n-i получаем конфигурацию q1(i+1)(2)*| n-i-1 . Поэтому после n итераций получится конфигурация 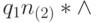
 выдаст 1, и цикл завершится с записью
выдаст 1, и цикл завершится с записью 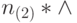 на ленте , из которой M4 сотрет * и оставит требуемый результат n(2) .
на ленте , из которой M4 сотрет * и оставит требуемый результат n(2) .
Отметим, что из приведенного примера и из задачи oldref(a) следует, что класс вычислимых на м.Т . арифметических функций не зависит от выбора унарного или двоичного кодирования аргументов и результатов. Это же справедливо и для троичной, десятичной и других позиционных систем счисления ( почему ?).
Задачи
Задача 9.1. Постройте м.Т . для функции копирования , не увеличивая исходный алфавит
Задача 9.2. Постройте программу м.Т ., которая выполняла бы перенос непустого слова в заданное место ленты , т.е. для любого слова  и n > 0 выполняла преобразование конфигураций :
и n > 0 выполняла преобразование конфигураций : 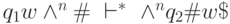 .
.
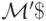 из леммы 9.1 на этапах 3 и 4.
из леммы 9.1 на этапах 3 и 4.
Задача 9.4. Докажите, что односторонняя м.Т .  построенная в лемме 9.2, корректно моделирует исходную м.Т .
построенная в лемме 9.2, корректно моделирует исходную м.Т . 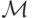 .
.
Задача 9.5. Другой, по сравнению с конструкцией леммы 9.2, подход к моделированию двухсторонней ленты на односторонней заключается в том, чтобы содержимое правой полуленты  хранить в четных ячейках
хранить в четных ячейках 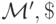 а содержимое левой полуленты — в нечетных, поместив в 1-ю ячейку специальный маркер. Постройте программу , реализующую этот подход (ее достоинство — увеличение алфавита ленты всего на 1 символ).
а содержимое левой полуленты — в нечетных, поместив в 1-ю ячейку специальный маркер. Постройте программу , реализующую этот подход (ее достоинство — увеличение алфавита ленты всего на 1 символ).
Задача 9.6. Достройте программу м.Т . из леммы 9.4 на этапах 1, 3 и 5.
Задача 9.7. Построить программы машин Тьюринга , вычисляющих следующие функции.
- Перевод из двоичной системы в унарную: f bu (n(2))= | n .
- Сложение и вычитание в двоичной системе: sum(n*m)=n+m и
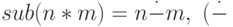 совпадает с — при n >= m и
совпадает с — при n >= m и 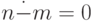 при m > n ).
при m > n ). - Умножение в двоичной системе: mul(n*m)= n x m . ( Реализуйте алгоритм умножения «в столбик».)
- Возведение в степень: exp(n*m)= n m .
- Извлечение квадратного корня:
 .
. - Логарифмирование:
 .
. - Деление:
 .
. - Остаток от деления: rest(n*m) = n mod m .
- Функция выбора аргумента:
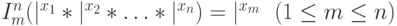 .
.
Задача 9.8. Используя машины Тьюринга из предыдущей задачи, построить программы машин Тьюринга , вычисляющих следующие функции.
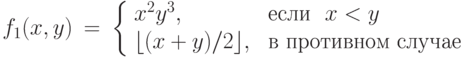


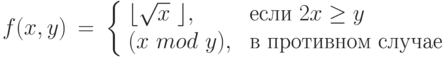
Задача 9.9. Докажите, что всякую арифметическую функцию f(x) , вычислимую на некоторой м. Т. 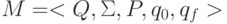 , можно также вычислить на м. Т. M’ ,, алфавит ленты которой содержит лишь два символа
, можно также вычислить на м. Т. M’ ,, алфавит ленты которой содержит лишь два символа  и | . (Указание: используйте для моделирования одного символа из
и | . (Указание: используйте для моделирования одного символа из  блок из нескольких подряд идущих ячеек, содержащих его код в алфавите
блок из нескольких подряд идущих ячеек, содержащих его код в алфавите 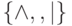 ) и замените каждую команду M группой команд, обрабатывающих соответствующий блок ячеек).
) и замените каждую команду M группой команд, обрабатывающих соответствующий блок ячеек).
Задача 9.10. Построить машину Тьюринга , определяющую по слову x в алфавите симметрично ли оно, т. е. вычисляющую функцию:
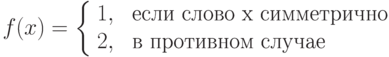
![x prec y Leftrightarrow exists i leq n [(x_1=y_1) ldots (x_</p><p><b>Задача 9.11</b>. Построить машину Тьюринга , сравнивающую два слова x=x<sub>1</sub>x<sub>2</sub>. x<sub>n</sub> и y=y<sub>1</sub>y<sub>2</sub>. y<sub>m</sub> в алфавите лексикографически: =y_) y_i )]](https://intuit.ru/sites/default/files/tex_cache/906eaf76ce1a1acb04eb948e9f81cef0.png) или для некоторого непустого слова x’ выполнено y = x x’ . Эта машина Тьюринга должна вычислять функцию:
или для некоторого непустого слова x’ выполнено y = x x’ . Эта машина Тьюринга должна вычислять функцию:
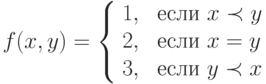
Источник: intuit.ru
Тьюрингово программирование
В этом разделе мы приведем примеры вычислений на машинах Тьюринга и рассмотрим некоторые общие приемы, позволяющие комбинировать программы различных МТ для получения более сложных вычислений.
Назовем заключительную конфигурацию стандартной, если в ней головка наблюдает первый значащий символ результата, который находится в 1-ой ячейке (т.е. в той же ячейке, где начиналось входное слово).
1. Построить машину Тьюринга, переводящую слово  в слово
в слово  , если внешний алфавит
, если внешний алфавит  .
.
2. Проверить работу машины Тьюринга над некоторым словом.
1. Опишем работу алгоритма, решающего задачу.
Будем обозначать состояния машины Тьюринга числами 0,1,2,…, причем 1 ‑ начальное, а 0 ‑ заключительное состояния.

Так как нам надо переписать слово в обратном порядке, то понадобится вспомогательный символ внешнего алфавита, который обозначим «*», т.е. .
Вначале с помощью команд  ;
;  заменяем
заменяем  на «*» и движемся влево. Признаком окончания слова будет считывание λ в состояниях 2 или 3. С помощью команд
на «*» и движемся влево. Признаком окончания слова будет считывание λ в состояниях 2 или 3. С помощью команд
 и
и 

печатаем символ , движемся вправо и переходим в состояние 4.
Запишем промежуточные конфигурации:

Если в состоянии 4 считываем символы а или b, то, не изменяя символы и состояние, движемся вправо. Это позволит пройти новое слово, которое строим, без изменений.
 ,
, 
Если в состоянии 4 считываем символ «*», то это значит, что новое слово пройдено и надо переходить в следующее состояние 5, чтобы дойти до остатков старого слова.

Если в состоянии 5 считываем символ «*», то движемся вправо, не меняя символ и состояние. Если в состоянии 5 считываем символы а или b, значит, дошли до остатков старого слова. Заменяем символы на «*», переходим в состояния 2 или 3 и движемся влево.
 ,
,  ,
, 
В состояниях 2 или 3, двигаясь влево, нужно пройти все символы «*», а также новое слово. Это позволят сделать команды:
 ,
,  ,
,  ,
,
 ,
,  ,
,  .
.
Признаком того, что все символы «*», а также новое слово пройдены, будет считывание λ в состояниях 2 или 3.
Запишем промежуточные конфигурации:

Дальше по циклу все символы перепишутся. Признаком того, что старое слово закончилось, является считывание символа λ в состоянии 5. Остается стереть все символы «*» и остановится в начале нового слова. Для этого понадобятся команды:
 ;
;  ;
;  ;
;  ;
;  .
.
Запишем все конфигурации:

Программу найденной машины Тьюринга представим таблицей
| AQ | ||||||
| λ | ‑ |  |
 |
‑ |  |
 |
| a |  |
 |
 |
 |
 |
 |
| b |  |
 |
 |
 |
 |
 |
| * | ‑ |  |
 |
 |
 |
 |

2. Проверим работу машины Тьюринга над словом .

Итак, проверка сделана, результат работы машины Тьюринга удовлетворяет требованиям, которые ставились в условии задачи.

1. Построить машину Тьюринга, вычисляющую числовую функцию .
2. Проверить работу построенной машины над некоторым набором значений.
1. Будем обозначать состояния машины Тьюринга  причем
причем  ‑ начальное, а
‑ начальное, а  ‑ заключительное состояния.
‑ заключительное состояния.
Набор значений аргументов  изображается словом
изображается словом  .
.
Аргумент  должен остаться без изменения, этого можно добиться с помощью команды
должен остаться без изменения, этого можно добиться с помощью команды  . Когда в состоянии
. Когда в состоянии  встретиться символ λ, значит, мы попали на символ, разделяющий изображения аргументов, переходим в состояние
встретиться символ λ, значит, мы попали на символ, разделяющий изображения аргументов, переходим в состояние  , а сам символ λ пока оставим без изменений с помощью команды
, а сам символ λ пока оставим без изменений с помощью команды  .
.
Далее набор единиц, изображающих аргумент  , проходим до конца. Для этого добавим команды:
, проходим до конца. Для этого добавим команды:  ;
;  .
.
Теперь с помощью «челночного» алгоритма удвоим количество единиц в блоке, изображающем вторую переменную.
Расширим алфавит, введя символ «*», т.е.  . Будем заменять единицы блока
. Будем заменять единицы блока  метками «*» следующим образом.
метками «*» следующим образом.
Получили машину Тьюринга с внешним алфавитом  , алфавитом внутренних состояний
, алфавитом внутренних состояний  и программой, записанной в виде следующей таблицы:
и программой, записанной в виде следующей таблицы:
| AQ |  |
 |
 |
 |
 |
 |
 |
 |
| λ |  |
 |
 |
 |
 |
‑ | ‑ | ‑ |
 |
 |
 |
 |
 |
 |
 |
 |
|
| * | ‑ | ‑ | ‑ | ‑ |  |
‑ | ‑ | ‑ |

2. Проверим работу алгоритма над изображением набора переменных . Применим эту машину к слову 11λ11. Вот последовательность конфигураций, возникающих в процессе работы машины (исходная конфигурация — стандартная начальная):

Нетрудно заметить, что данная машина Тьюринга перерабатывает исходное слово  в слово
в слово  , т.е.
, т.е.  .
.
Источник: studopedia.org