Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы
Исходник программы возведения числа в степень
Создадим программу, которая сможет возвести число в степень в консоли, используя метод Math.Pow.
Итак, создаем проект, затем объявляем две переменные.
Мы неоригинально назвали эти переменные a и b и указали их типом данных double — 64-разрядный тип повышенной точности с плавающей точкой, более функциональный, чем целочисленный int или менее точный float, но и занимающий больше памяти. В принципе, можно использовать любой тип из перечисленных — всё упирается в ваши нужды и запросы.
Источник: vscode.ru
Функция Power

Функция Power в Паскале (и многих других языках программирования) выполняет возведение числа в степень.
42 Задача: Возведение числа в степень при помощи Python
Синтаксис для вещественных чисел:
function Power(Base: Double; Expon: Double) : Double;
Синтаксис для целых чисел:
function Power(Base: LongInt; Expon: LongInt) : LongInt;
Эта функция возводит число Base в степень Expon и возвращает результат. В реальности функция возвращает результат выражения:
- В документации сказано, что функция объявлена в модуле SYSTEM. Однако без подключения модуля MATH компилятор выдаёт ошибку. Из этого следует, что на самом деле функция объявлена в модуле MATH.
- В документации приведён синтаксис как для целых, так и для вещественных чисел. Однако на самом деле функция работает только с вещественными числами. При попытке использовать целые числа компилятор также выдаёт ошибку.
- Возможно, в более новых версиях эти проблемы уже исправлены. Но у меня было именно так (версия FPC 3.0.0).
Пример использования функции Power
Пример приведён ниже:
program funcpower; uses Math; var x, y, z : single; begin x := 2; y := 3; z := Power(x, y); //Z = X в степени Y WriteLn(z:0:2); ReadLn; end.
Здесь мы число 2 (переменная Х) возводим в степень 3 (переменная Y), то есть вычисляем следующую формулу:
Z = X Y
Обратите внимание на подключенный модуль MATH.
Эта статья входит в раздел о подпрограммах модуля SYSTEM. И по идее описания функции Power здесь не должно быть. Но, так как в документации сказано, что функция Power объявлена в модуле SYSTEM, я решил включить данную статью именно в этот раздел (я же не виноват, что в документации косяк))).
Возведение в степень в Паскале
Возведение в степень в Паскале можно выполнить и без какой-то специальной функции, используя функцию вычисления натурального логарифма и функцию вычисления экспоненты. О том, как это сделать, я рассказал здесь.
Однако, если есть специальная функция для возведения числа в степень, то почему бы ей и не воспользоваться? С одной стороны. С другой стороны — эта функция совершенно неожиданно требует подключения модуля MATH.
В документации сказано, что по сути функция Power работает по формуле возведения в степень в Паскале:
Однако, если мы будем делать именно так, эта формула будет неправильно работать с отрицательными числами, потому что в документации сказано, что функция Ln работает только с положительными числами.
Так что функция Power в реальности несколько сложнее, чем приведённая выше формула.
Поэтому для разминки мы напишем свой аналог функции Power, который будет работать правильно. Но для начала вспомним как вычисляется степень числа:
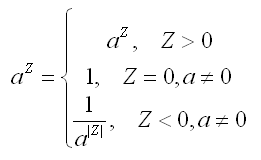
Также напомню, что любое число в нулевой степени равно 1, а ноль в любой степени равен 0 (кроме нуля в нулевой — ноль в нулевой степени не определён, но мы будем возвращать в таких случаях ноль, хотя функция Power возвращает 1).
А теперь наш аналог функции Power:
function AVPower(Base: Double; Expon: Double) : Double; var m : byte; i : integer; Res : Double; begin m := 0; if Expon < 0 then m := 1 //Отрицательная степень else if Expon = 0 then m := 2 //Нулевая степень else m := 3; //Положительная степень if Base < 0 then m := 10 + m //Отрицательное число else if Base = 0 then m := 20 + m //Число равно 0 else m := 30 + m; //Положительное число case m of 11 : //Отрицательное число, отрицательная степень begin //Если Expon — не целое число, то получаются комплексные числа Res := 1 / Exp(Abs(Expon) * Ln(Abs(Base))); i := Round(Expon); if Odd(i) then Res := -1 * Res; end; 12, 32 : //Нулевая степень Res := 1; 13 : //Отрицательное число, положительная степень begin //Если Expon — не целое число, то получаются комплексные числа Res := Exp(Expon * Ln(Abs(Base))); i := Round(Expon); if Odd(i) then Res := -1 * Res; end; 21..23 : //Число равно нулю Res := 0; 31 : //Положительное число, отрицательная степень Res := 1 / Exp(Abs(Expon) * Ln(Base)); 33 : //Положительное число, положительная степень Res := Exp(Expon * Ln(Base)); end; AVPower := Res; end;
Я сознательно немного всё усложнил, чтобы вас запутать )))
Пример использования функций Power и её аналога в программе:
x := 2; y := 3; z := Power(x, y); //Z = X в степени Y WriteLn(z:0:2); z := AVPower(x, y); //Z = X в степени Y WriteLn(z:0:2);
Здесь есть один подвох — если вы попытаетесь возвести отрицательное число в не целую степень, например, так:
то стандартная функция Power вызовет ошибку во время выполнения программы. В своём аналоге я этого избежал, но надо понимать, что результат в этом случае будет неправильным (хотя с моей точки зрения это всё-равно лучше, чем аварийное завершение программы).
Это происходит потому, что при таком раскладе результатом являются комплексные числа, а операции с комплексными числами выполняются по другим правилам.
В реальных программах подобные ситуации надо дополнительно обрабатывать (хотя бы предупреждать пользователя о том, что при отрицательном основании и не целой степени функция вернёт неправильный результат).
Ещё в моей функции используется функция Odd, о которой я ещё не рассказывал. Вкратце скажу, что она определяет, является ли число чётным. Более подробно о ней расскажу в отдельной статье.
Источник: info-master.su
Нахождение степени числа с использованием рекурсии
Программа принимает на вход число и его степень, и при помощи рекурсии вычисляет результат.
Решение задачи
- Принимаем на вход число и значение его степени, записываем их в отдельные переменные.
- Передаем эти переменные в качестве аргументов в рекурсивную функцию.
- Определяем в качестве базового условия рекурсии равенство степени 1 . В этом случае функция выводит само число, так как любое число в степени 1 равно само себе.
- В противном случае мы выводим произведение числа на эту же функцию, в которой второй аргумент, степень, уменьшен на 1 .
- Выводим конечный результат на экран.
- Конец.
Исходный код
Ниже дан исходный код, который осуществляет возведение числа в степень с использованием рекурсии. Результаты работы программы также даны ниже.
def power(base, exp): if (exp == 1): return (base) if (exp != 1): return (base * power(base, exp — 1)) base = int(input(«Введите число: «)) exp = int(input(«Введите его степень: «)) print(«Результат возведения в степень равен:», power(base, exp))
Объяснение работы программы
- Принимаем на вход число и значение его степени, записываем их в отдельные переменные base и exp соответственно.
- Передаем эти переменные в качестве аргументов в рекурсивную функцию power() .
- Определяем в качестве базового условия рекурсии exp == 1 . В этом случае функция выводит само число из переменной base , так как любое число в степени 1 равно само себе.
- В противном случае мы выводим произведение числа на эту же функцию, в которой второй аргумент (степень) уменьшен на единицу: base * power(base, exp — 1) . Таким образом мы накапливаем произведение числа, хранящегося в переменной base , самого на себя ровно exp раз, что эквивалентно возведению числа base в степень exp .
- Выводим конечный результат на экран.
Результаты работы программы
Пример 1: Введите число: 2 Введите его степень: 5 Результат возведения в степень равен: 32 Пример 2: Введите число: 5 Введите его степень: 3 Результат возведения в степень равен: 125
Источник: pythonist.ru