Формулировка. Даны натуральные числа x и n (которое также может быть равно 0). Вычислить x n .
Решение. Для того чтобы решить эту задачу, вспомним определение степени с натуральным показателем: запись x n означает, что число x умножено само на себя n раз.
Сразу из определения видно, что здесь заранее известно количество повторений при вычислении результата, так что задача легко решается через цикл for. Выходит, мы копируем исходное число x в некоторую переменную res (от англ. result– «результат»), а затем просто умножаем его на x n раз? Не стоит торопиться с ответом.
Рассмотрим пример: 3 4 = 3 * 3 * 3 * 3 = 81. Если посмотреть на эту запись, то мы видим, что возведение в четвертую степень как выражение содержит четыре слагаемых, но только три операции, так как мы с первого шага домножаем число 3 на три тройки. Тогда реализация идеи из абзаца выше будет давать число в степени на 1 больше, чем требуется.
Какой можно придумать выход? Например, можно сократить цикл на одну операцию, но что тогда будет при вычислении нулевой степени? Как известно, любое число в нулевой степени дает 1, а здесь при вводе в качестве n нуля приведет к тому, что не будет осуществлен вход в цикл (так как не существует целочисленного отрезка от 1 до 0) и в итоге на выход так и пойдет исходное число x.
Напишите программу, проверяющую число, введенное с клавиатуры на четность. Домашнее задание. C++ #2.
А что, если изменить схему умножения так: 3 4 = 1 * 3 * 3 * 3 * 3 = 81? Так мы можем сравнять показатель степени и число требуемых операций, да и с нулевой степенью все становится просто, так как при вводе в качестве n нуля не будет осуществляться вход в цикл и на выход в программе пойдет число 1!
Теперь алгоритм на естественном языке:
1) Ввод x и n;
2) Присваивание переменной res числа 1;
3) Запуск цикла, при котором i изменяется от 1 до n. В цикле:
4) Вывод переменной res.
Код:
- program Exponentiation;
- var
- x, n, i, res: word;
- begin
- readln(x, n);
- res := 1;
- for i := 1 to n do begin
- res := res * x
- end;
- writeln(res)
- end.
Кстати, стоит понимать, что объявление переменной res при использовании типа word достаточно условно, так как этот тип принимает значения от 0 до 65535, что на единицу меньше числа 256 2 , хотя вводить в программу можно числа, предполагающие возведение в более высокую степень. Так как в условии задачи не сказано ничего о том, в каком числовом промежутке по x и n она должна выдавать корректный ответ, оставим это в таком виде, достаточном для проверки приложения на работоспособность.
Источник: pascalzadachi.ru
c_sharp_vse_(14.12.13) / kudrina_e_v_ogneva_m_v_portenko_m_s_programmirovanie_na_yazy / index.files / 7 / Sm7
Решение многих задач связано с нахождением суммы или произведения элементов заданной последовательности. В данном разделе мы рассмотрим основные приемы вычисления конечных сумм и произведений.
9 Cтроки и операции над ними Python
Пусть 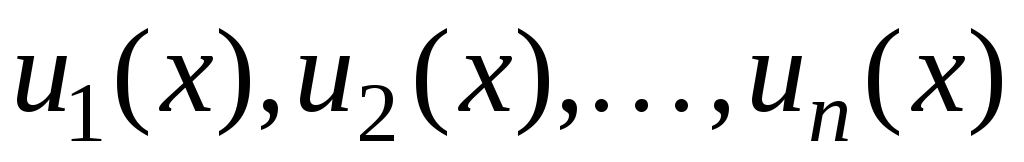 — произвольная последовательность n функций. Будем рассматривать конечную сумму вида
— произвольная последовательность n функций. Будем рассматривать конечную сумму вида 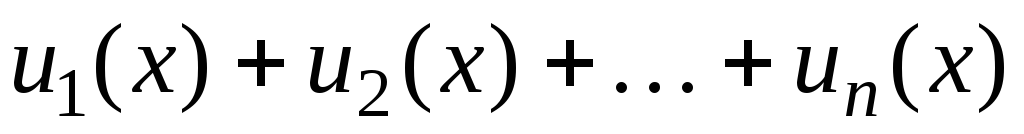 . Такую сумму можно записать более компактно, используя следующее обозначение:
. Такую сумму можно записать более компактно, используя следующее обозначение: 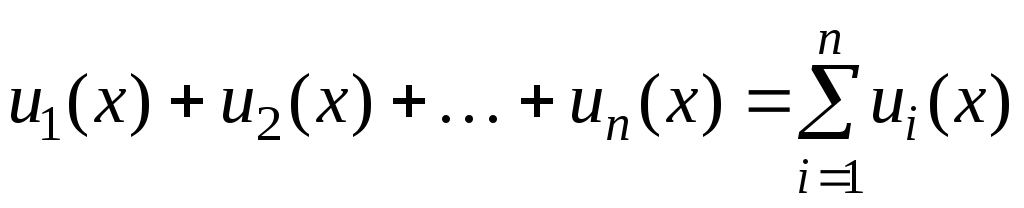 . При
. При 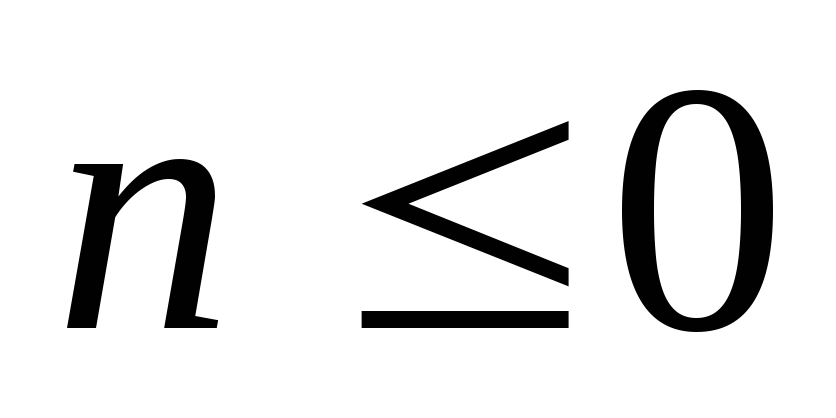 значение суммы равно 0.
значение суммы равно 0.
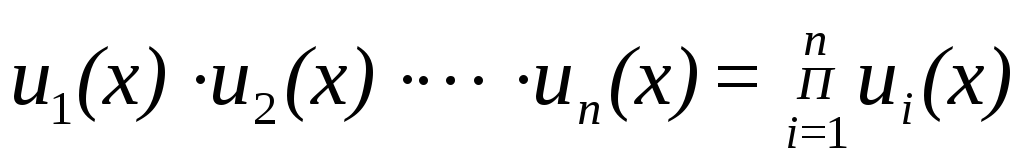
В дальнейшем будем также использовать сокращенную запись для конечного произведения данной последовательности, которая выглядит следующим образом: .
- Написать программу, которая подсчитывает сумму натуральных чисел от 1 до n (n1).
Указания по решению задачи. Пусть sn — сумма натуральных чисел от 1 до n. Тогда sn=1+2+…+(n-1)+n=(1+2+…+(n-1))+n=sn-1+n, s0=0. Мы пришли к рекуррентному соотношению s0=0, sn=sn-1+n, которым мы можем воспользоваться для подсчета суммы. Соотношение sn=sn-1+n говорит о том, что сумма на n-ном шаге равна сумме, полученной на предыдущем шаге, плюс очередное слагаемое. static void Main() < Console.Write(«Ввведите значение n: «); int n=int.Parse(Console.ReadLine()); int s=0; for (int i=1; i>
- Написать программу, которая подсчитывает n! для вещественного x и натурального n.
Указание по решению задачи. Из свойства факториала 0!=1!=1, n!=1*2*3*…*n, n!=(n-1)!n. Следовательно, факториал можно вычислять, используя рекуррентное соотношение b0=1, bn=bn-1*n. static void Main() < Console.Write(«Ввведите значение n: «); int n=int.Parse(Console.ReadLine()); int f=1; for (int i=1; i!=», n, f); >
- Написать программу для подсчета суммы
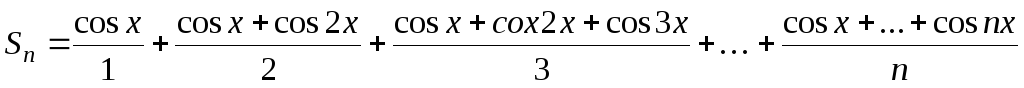 , где х – вещественное число, n – натуральное число.
, где х – вещественное число, n – натуральное число.
Указания по решению задачи. Если пронумеровать слагаемые, начиная с 1, то мы увидим, что номер слагаемого совпадает со значением знаменателя. Рассмотрим каждый числитель отдельно: 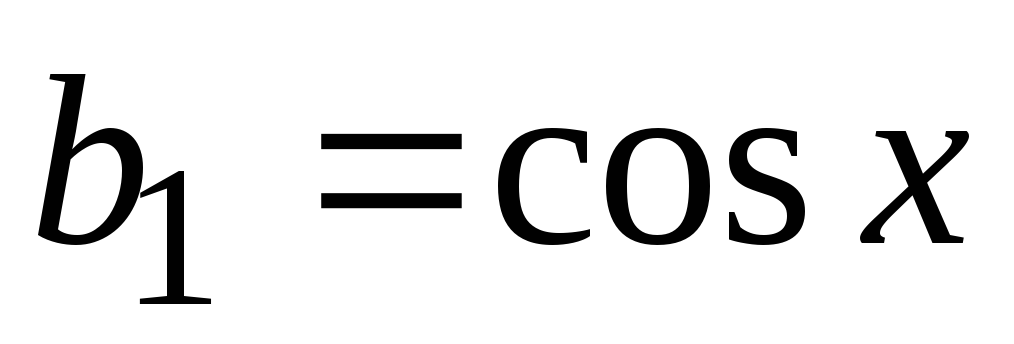 ,
, 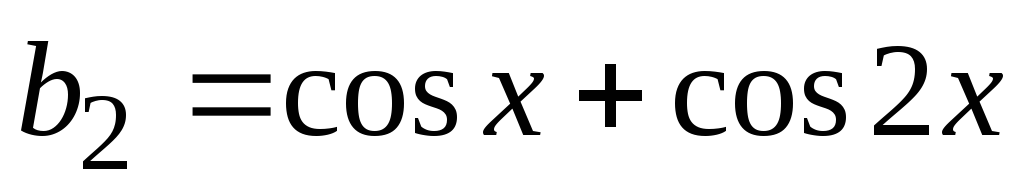 ,
, 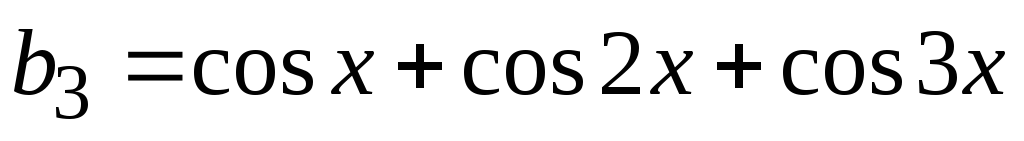 … Эту последовательность можно представить рекуррентным соотношением b0=0, bn=bn-1+cosnx(1). Теперь сумму можно представить следующим образом
… Эту последовательность можно представить рекуррентным соотношением b0=0, bn=bn-1+cosnx(1). Теперь сумму можно представить следующим образом 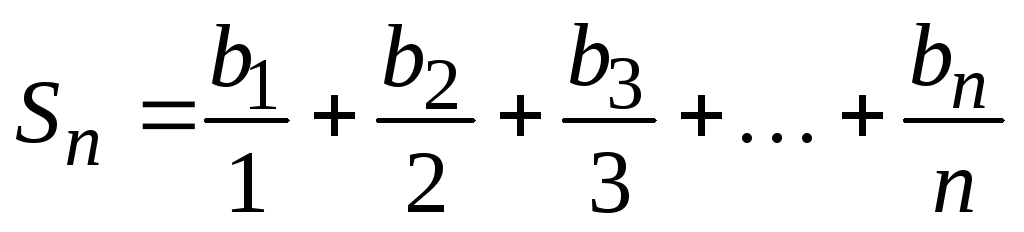 , а для нее справедливо рекуррентное соотношение S0=0,
, а для нее справедливо рекуррентное соотношение S0=0, 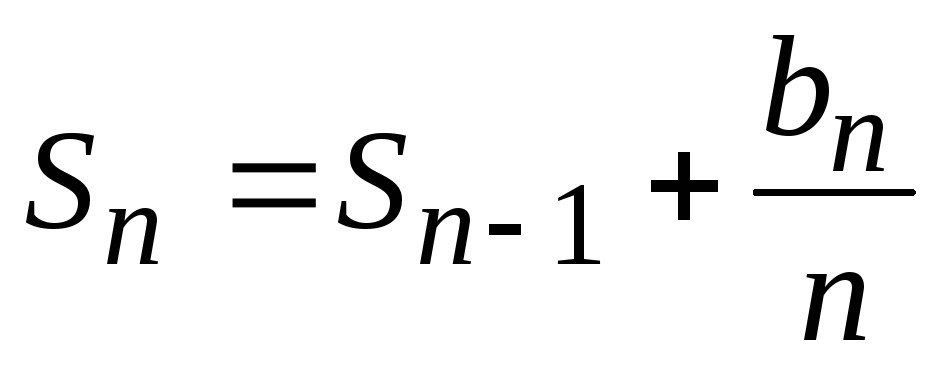 (2). При составлении программы будем использовать формулы (1-2). static void Main() < Console.Write(«Ввведите значение n: «); int n=int.Parse(Console.ReadLine()); Console.Write(«Ввведите значение x: «); double x=double.Parse(Console.ReadLine()); double b=0, s=0; for (int i=1; iConsole.WriteLine(«s=»,s); >
(2). При составлении программы будем использовать формулы (1-2). static void Main() < Console.Write(«Ввведите значение n: «); int n=int.Parse(Console.ReadLine()); Console.Write(«Ввведите значение x: «); double x=double.Parse(Console.ReadLine()); double b=0, s=0; for (int i=1; iConsole.WriteLine(«s=»,s); >
- Написать программу для подсчета суммы
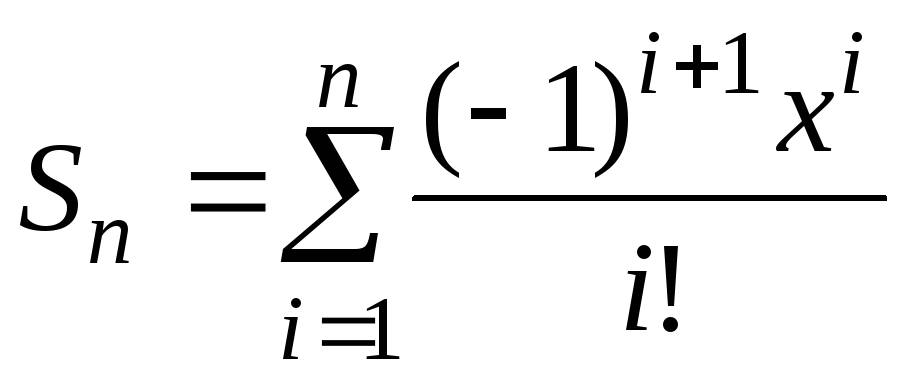 , где х – вещественное число, n – натуральное число.
, где х – вещественное число, n – натуральное число.
Указания по решению задачи. Перейдем от сокращенной формы записи к развернутой, получим 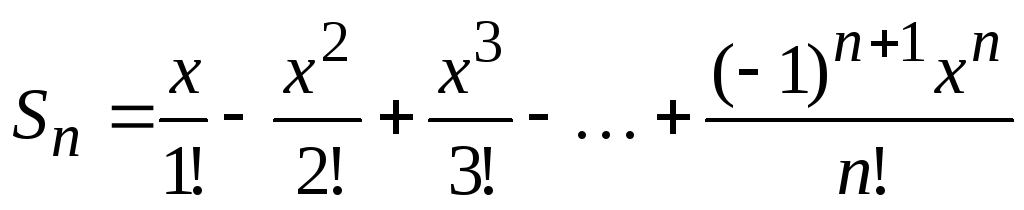 . Каждое слагаемое формируется по формуле
. Каждое слагаемое формируется по формуле 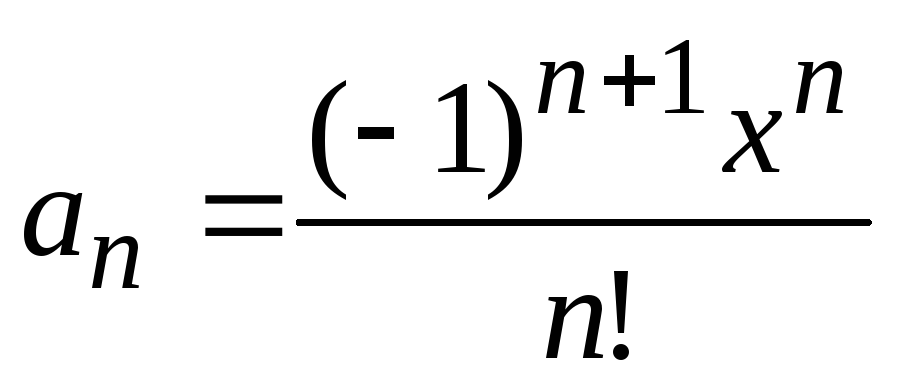 . Если в эту формулу подставить n=0, то получим
. Если в эту формулу подставить n=0, то получим 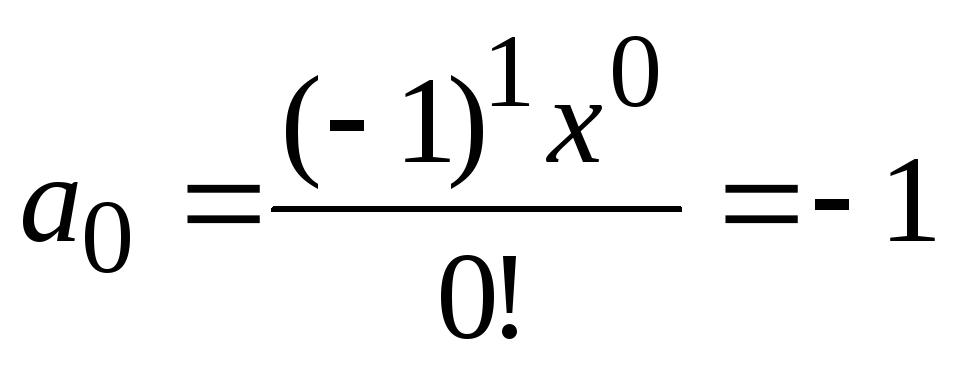 . Чтобы не вводить несколько рекуррентных соотношений (отдельно для числителя, отдельно для знаменателя), представим общий член последовательности слагаемых с помощью рекуррентного соотношением вида
. Чтобы не вводить несколько рекуррентных соотношений (отдельно для числителя, отдельно для знаменателя), представим общий член последовательности слагаемых с помощью рекуррентного соотношением вида 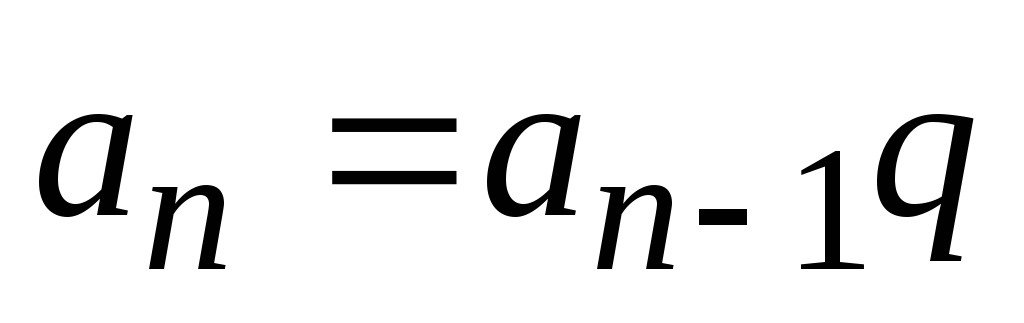 , где q для нас пока не известно. Найти его можно из выражения
, где q для нас пока не известно. Найти его можно из выражения 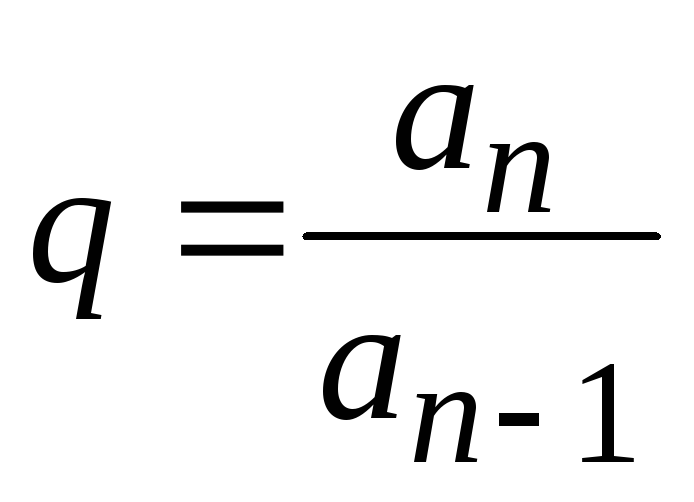 . Произведя необходимые расчеты, получим, что
. Произведя необходимые расчеты, получим, что 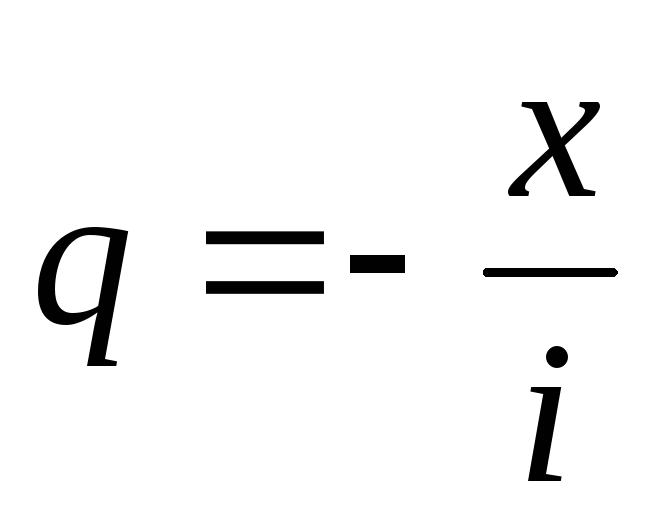 . Следовательно, для последовательности слагаемых мы получили рекуррентное соотношение
. Следовательно, для последовательности слагаемых мы получили рекуррентное соотношение 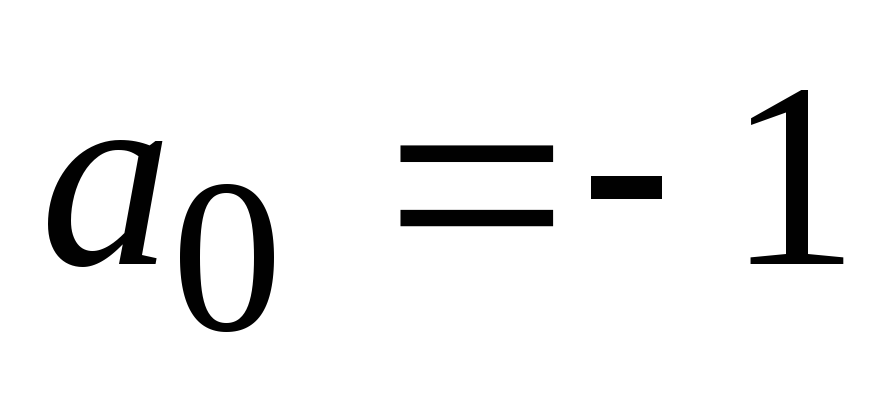 ,
, 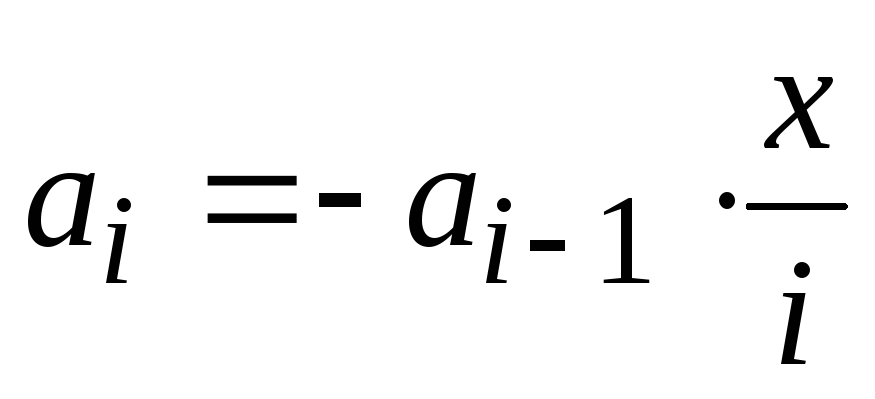 (3). А всю сумму, по аналогии с предыдущими примерами, можно представить рекуррентным соотношением: S0=0,
(3). А всю сумму, по аналогии с предыдущими примерами, можно представить рекуррентным соотношением: S0=0, 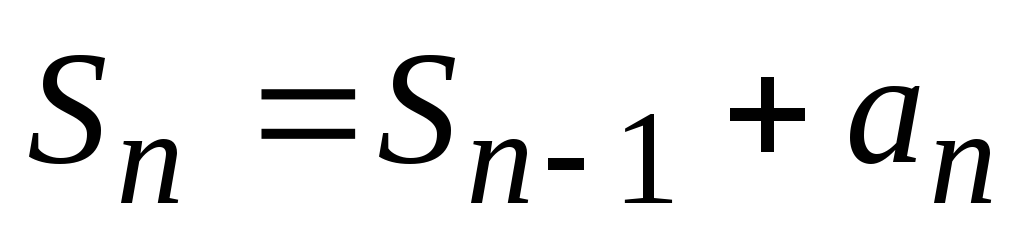 (4). Таким образом, при составлении программы будем пользоваться формулами (3-4). using System; namespace Hello < class Program < static void Main() < Console.Write(«Ввведите значение n: «); int n=int.Parse(Console.ReadLine()); Console.Write(«Ввведите значение x: «); double x=double.Parse(Console.ReadLine()); double a=-1, s=0; for (int i=1; iConsole.WriteLine(«s=»,s); > > >Вычисление бесконечных сумм Будем теперь рассматривать бесконечную сумму вида
(4). Таким образом, при составлении программы будем пользоваться формулами (3-4). using System; namespace Hello < class Program < static void Main() < Console.Write(«Ввведите значение n: «); int n=int.Parse(Console.ReadLine()); Console.Write(«Ввведите значение x: «); double x=double.Parse(Console.ReadLine()); double a=-1, s=0; for (int i=1; iConsole.WriteLine(«s=»,s); > > >Вычисление бесконечных сумм Будем теперь рассматривать бесконечную сумму вида 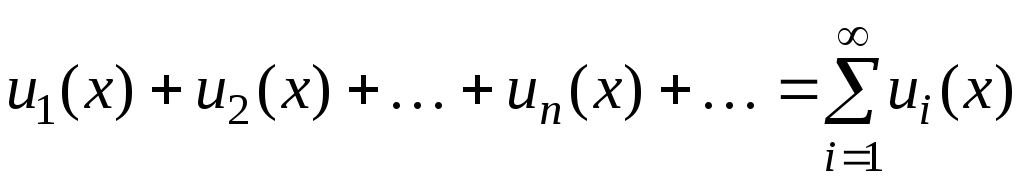 . Это выражение называется функциональным рядом. При различных значениях x из функционального ряда получаются различные числовые ряды
. Это выражение называется функциональным рядом. При различных значениях x из функционального ряда получаются различные числовые ряды 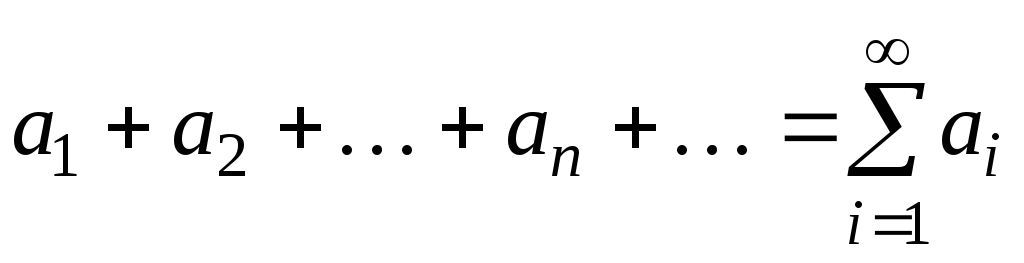
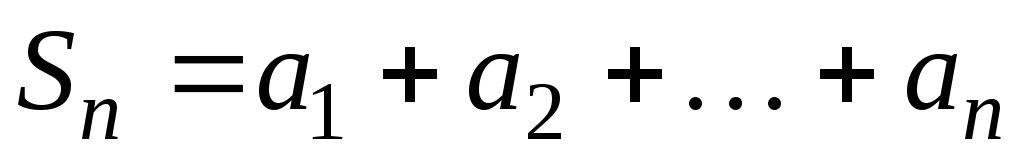 при
при 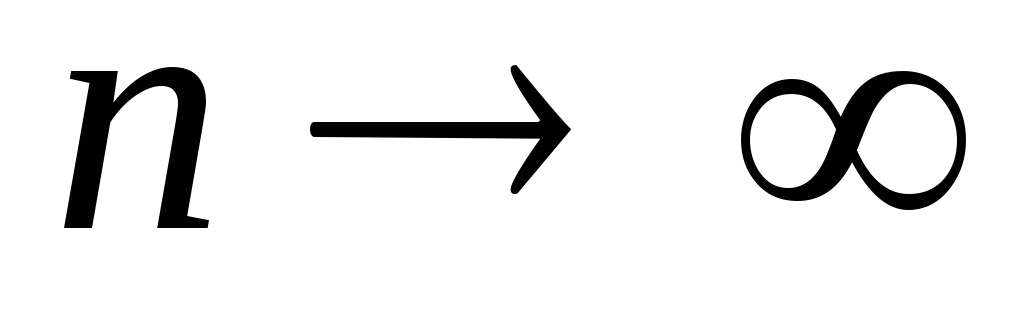 имеет предел, в противном случае, ряд называется расходящимся. Ряд может сходиться лишь при условии, что общий член ряда
имеет предел, в противном случае, ряд называется расходящимся. Ряд может сходиться лишь при условии, что общий член ряда 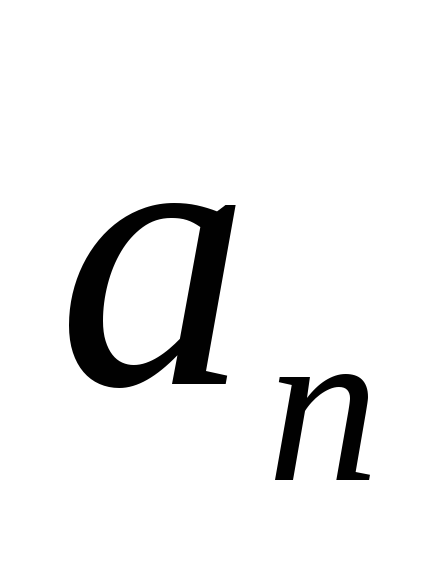 при неограниченном увеличении его номера стремится к нулю:
при неограниченном увеличении его номера стремится к нулю: 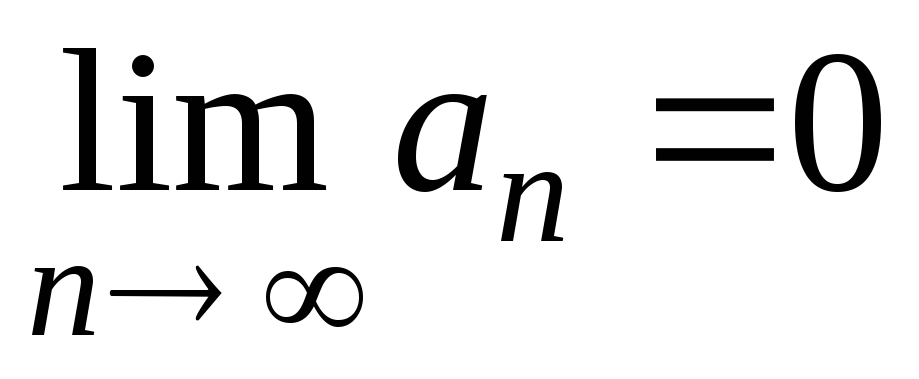 . Это необходимый признак сходимости для всякого ряда. В случае бесконечной суммы будем вычислять ее с заданной точностью e. Cчитается, что требуемая точность достигается, если вычислена сумма нескольких первых слагаемых и очередное слагаемое оказалось по модулю меньше чем е, то есть это слагаемое на результат практически не влияет. Тогда его и все последующие слагаемые можно не учитывать. Пример. Написать программу для подсчета суммы
. Это необходимый признак сходимости для всякого ряда. В случае бесконечной суммы будем вычислять ее с заданной точностью e. Cчитается, что требуемая точность достигается, если вычислена сумма нескольких первых слагаемых и очередное слагаемое оказалось по модулю меньше чем е, то есть это слагаемое на результат практически не влияет. Тогда его и все последующие слагаемые можно не учитывать. Пример. Написать программу для подсчета суммы 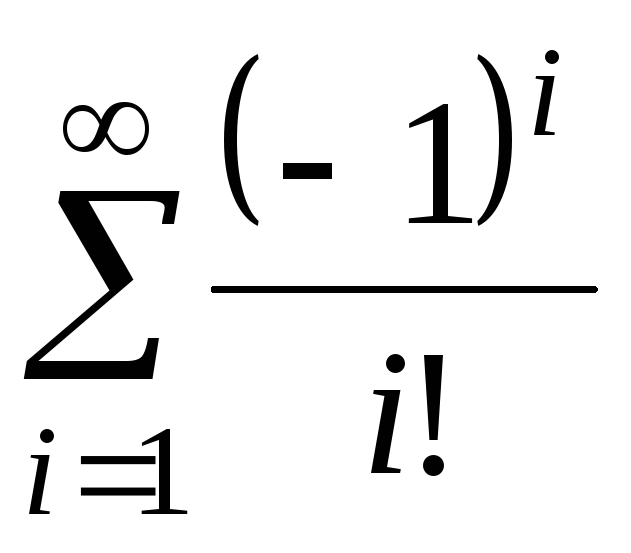 с заданной точностью е (е>0). Указание по решению задачи. Рассмотрим, что представляет из себя заданный ряд:
с заданной точностью е (е>0). Указание по решению задачи. Рассмотрим, что представляет из себя заданный ряд: 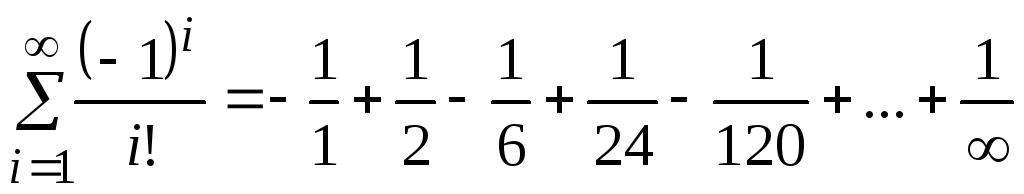 . Как видим, общий член ряда с увеличением значения i стремится к нулю. Поэтому данную сумму можно вычислить, но только с определенной точностью e. Заметим также, что последовательность слагаемых можно выразить с помощью рекуррентного соотношения a1=-1,
. Как видим, общий член ряда с увеличением значения i стремится к нулю. Поэтому данную сумму можно вычислить, но только с определенной точностью e. Заметим также, что последовательность слагаемых можно выразить с помощью рекуррентного соотношения a1=-1, 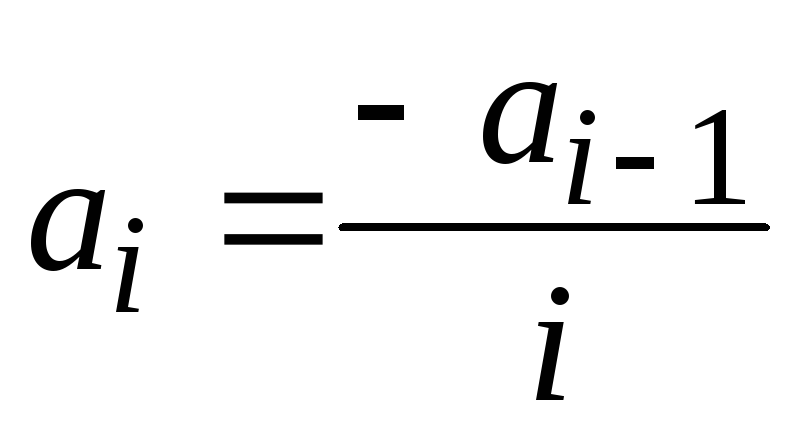 , а всю сумму — с помощью рекуррентного соотношения S0=0, Sn=Sn-1+an. (Данные рекуррентные соотношения выведите самостоятельно.) using System; namespace Hello < class Program < static void Main() < Console.Write(«Задайте точность вычислений е: «); double e=double.Parse(Console.ReadLine()); double a=-1, s=0; for (int i=2; Math.Abs(a)>=e; ++i) < s+=a; a/=-i; >Console.WriteLine(«s=»,s); > > >Практическое заданиеЗамечание. При решении задач производить обработку следующих исключительных ситуаций: ввода пользователем недопустимых значений и переполнения при вычислении математических выражений. I. Для заданного натурального n и действительного х подсчитать следующие суммы: 1)
, а всю сумму — с помощью рекуррентного соотношения S0=0, Sn=Sn-1+an. (Данные рекуррентные соотношения выведите самостоятельно.) using System; namespace Hello < class Program < static void Main() < Console.Write(«Задайте точность вычислений е: «); double e=double.Parse(Console.ReadLine()); double a=-1, s=0; for (int i=2; Math.Abs(a)>=e; ++i) < s+=a; a/=-i; >Console.WriteLine(«s=»,s); > > >Практическое заданиеЗамечание. При решении задач производить обработку следующих исключительных ситуаций: ввода пользователем недопустимых значений и переполнения при вычислении математических выражений. I. Для заданного натурального n и действительного х подсчитать следующие суммы: 1) 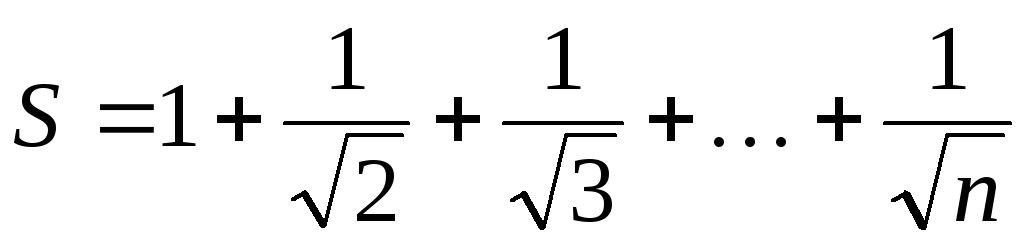 ; 2)
; 2)  3) S = 1!+2!+3!+…+n!; 4)
3) S = 1!+2!+3!+…+n!; 4)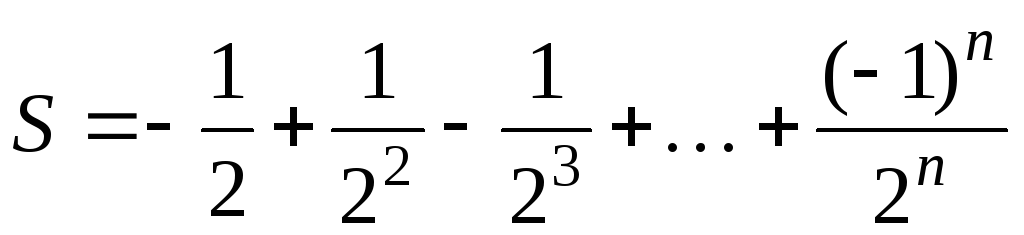 . II. Для заданного натурального k и действительного x подсчитать следующие выражения: 1)
. II. Для заданного натурального k и действительного x подсчитать следующие выражения: 1) 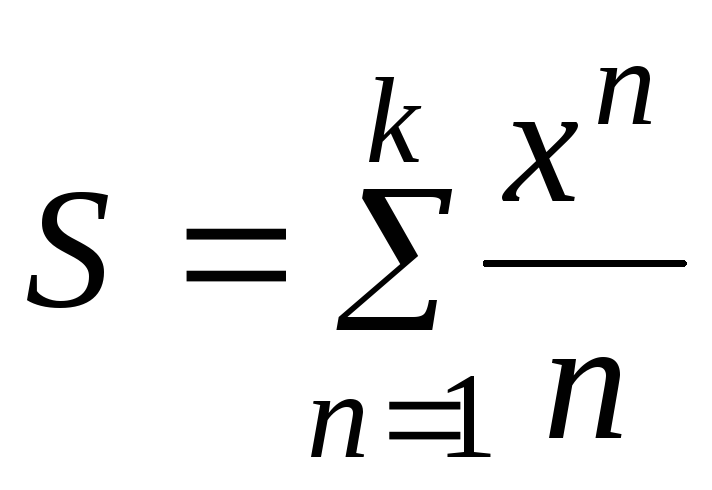 2)
2) 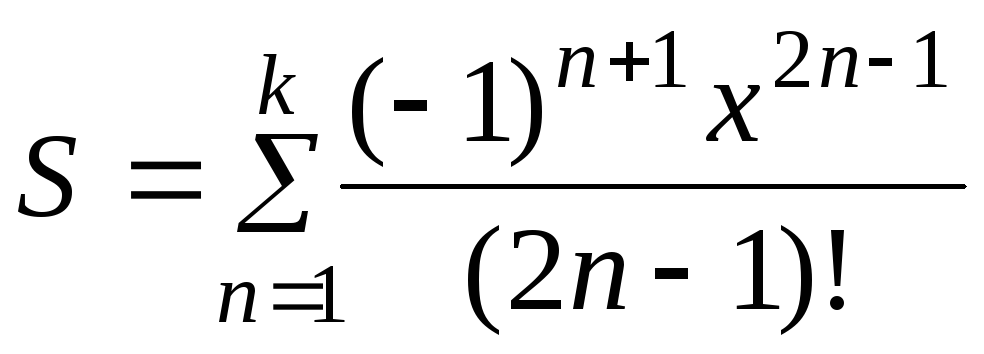 3)
3) 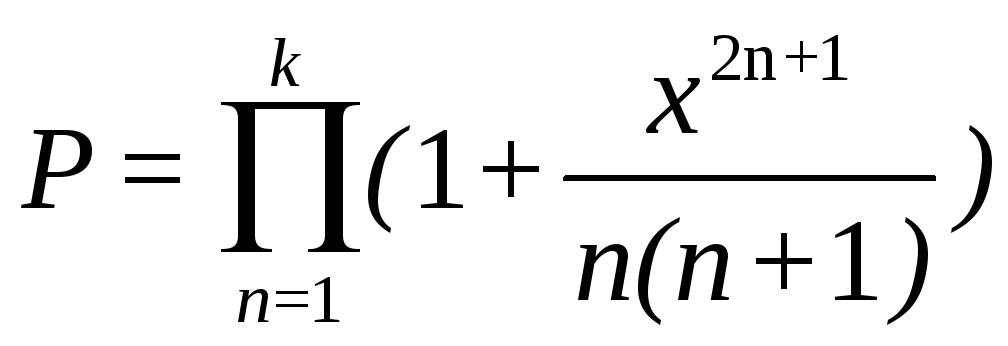 4)
4) 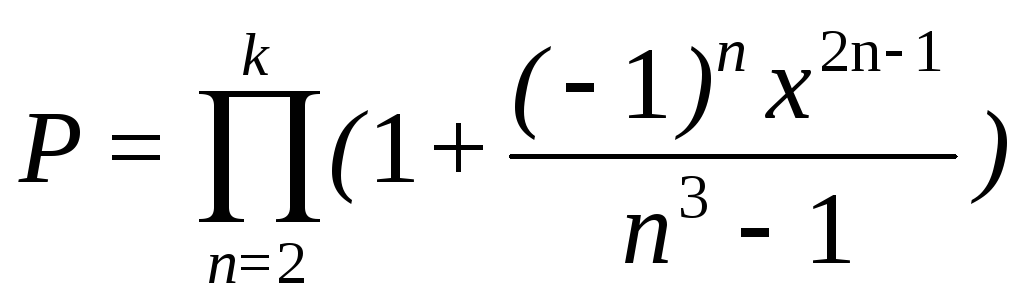 III. Вычислить бесконечную сумму ряда с заданной точностью е (e>0). 1)
III. Вычислить бесконечную сумму ряда с заданной точностью е (e>0). 1) 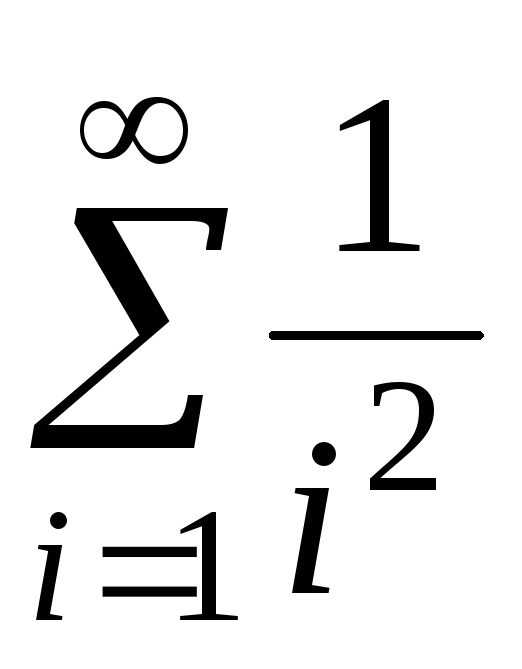 2)
2) 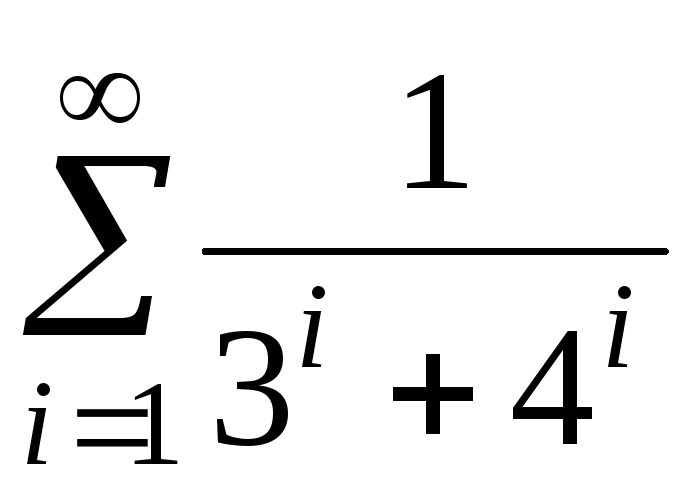 3)
3) 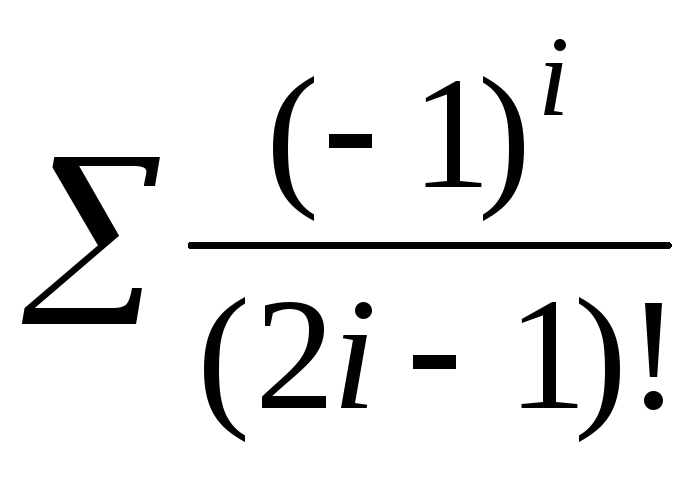 4)
4) 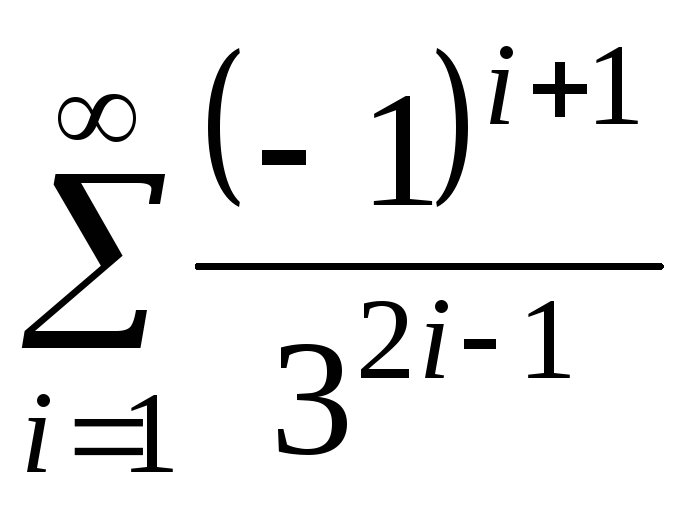 IV. Вычислить и вывести на экран значение функции F(x) на отрезке [a,b] c шагом h=0.1 с точностью e. Результат работы программы представить в виде следующей таблицы:
IV. Вычислить и вывести на экран значение функции F(x) на отрезке [a,b] c шагом h=0.1 с точностью e. Результат работы программы представить в виде следующей таблицы:
| № | Значение x | Значение функции F(x) | Количество просуммированных слагаемых n |
| 1 | |||
| 2 | |||
| … |
Замечание. При решении задачи использовать вспомогательную функцию.
- F(x) =
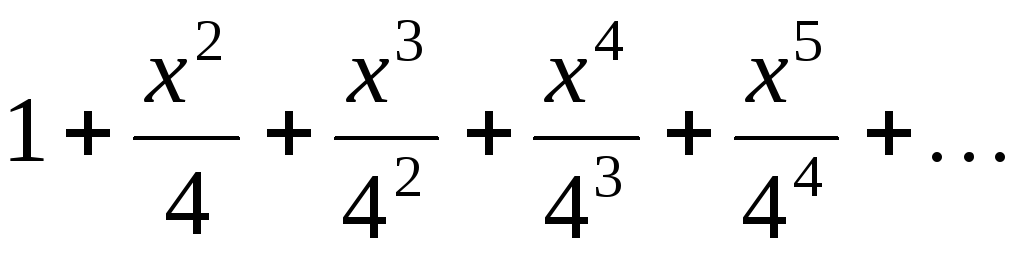 , x [0.1; 0.9].
, x [0.1; 0.9]. - F(x) =
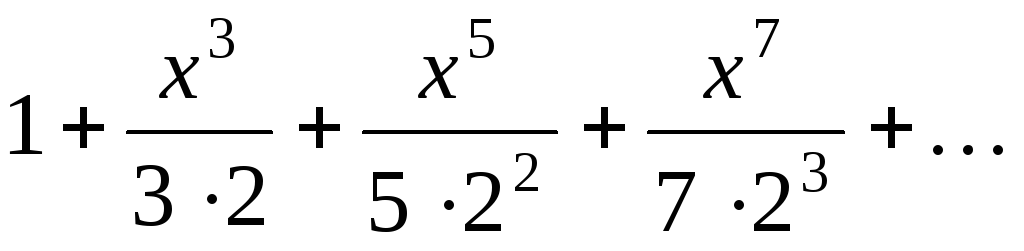 , x [0; 0.99].
, x [0; 0.99]. - F(x)=
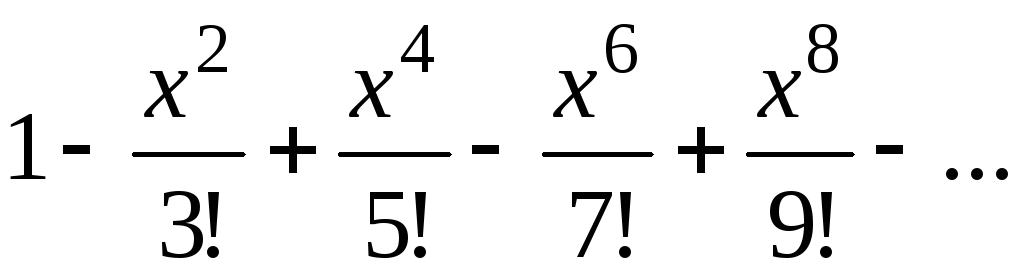 , x [0, 1].
, x [0, 1]. - F(x) =
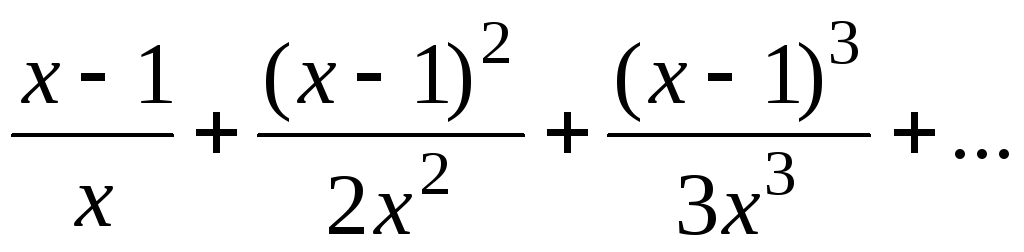 , x [1; 2].
, x [1; 2].
4
Источник: studfile.net
Задание 1 — Обработка числовых данных (лабораторная по Си)
Лабораторная работа для школ и вузов по решению задач по обработке числовых данных с помощью ветвления и циков на языке C (Си). Перечень задач лабораторной работы (клик по ссылке направляет на решение задачи, если таковое имеется):
Скачать файл лабораторной и все исходные коды программ в архиве:


Также вы можете заказать решение своих лабораторных работ на языке C++ и многих других:
№2: Подсчитать количество натуральных чисел n (111
#include int main() < int i, count = 0; for (i = 111; i
№3: Подсчитать количество натуральных чисел n (102
#include int main() < int i, count = 0; for (i = 102; i
№4: Подсчитать количество натуральных чисел n (11
#include int main() < int i; for (i = 11; i 100 i / 100 == i % 10) printf(«%dn», i); return 0; >
№5: Подсчитать количество цифр в десятичной записи целого неотрицательного числа n.
#include int main() < int n, count = 0; printf(«Enter n: «); scanf(«%d», while (n >0) < count++; n /= 10; >printf(«Number of digits: %d», count); return 0; >
№6: Определить, верно ли, что куб суммы цифр натурального числа n равен n^2.
#include int main() < int n, square, cube, sum = 0; printf(«Enter n: «); scanf(«%d», square = n * n; while (n >0) < sum = sum + (n % 10); n /= 10; >cube = sum * sum * sum; if (cube == square) printf(«True»); else printf(«False»); return 0; >
№7: Определить, является ли натуральное число n степенью числа 3.
#include int main() < int n; printf(«Enter n: «); scanf(«%d», while (n % 3 == 0) n /= 3; if (n == 1) printf(«The number is a power of 3.»); else printf(«The number is not a power of 3.»); return 0; >
№8: Для данного вещественного числа a среди чисел 1, 1 + (1/2), 1 + (1/2) + (1/3), . найти первое, большее a.
#include int main() < int n = 1; float a, num = 0; printf(«Enter a: «); scanf(«%f», while (num < a) < num += (1.0 / n++); >printf(«Answer: %f», num); return 0; >
№9: Для данного вещественного положительного числа a найти наименьшее целое положительное n такое, что 1 + 1/2 + 1/3 + . + 1/n > a.
#include int main() < int n = 1; float a, count = 1.0; scanf(«%f», while (count < a) < n++; count = count + (1.0 / n); >printf(«%d», n); return 0; >
№11: Дано натуральное число n. Найти значение числа, полученного следующим образом: из записи числа n выбросить цифры 0 и 5, оставив прежним порядок остальных цифр.
#include int main() < int n = 1; float a, count = 1.0; scanf(«%f», while (count < a) < n++; count = count + (1.0 / n); >printf(«%d», n); return 0; >
№13: Дано натуральное число n. Получить все его натуральные делители.
#include int main() < int n, i; scanf(«%d», for (i = 1; i
№14: Дано целое число m > 1. Получить наибольшее целое k, при котором 4^k = 2 и делится только на 1 и на себя).
#include int main() < int n, i = 0, i1, k = 1, k1 = 0; scanf(«%d», while (n >i) < k++; for (i1 = 1; i1 k1 = 0; > return 0; >
№18: Распечатать первые n чисел Фибоначчи (f0 = 1; f1 = 1; fk+1 = fk-1+ fk; k = 1, 2, 3, . ).
#include int main() < int n, i, f0 = 1, f1 = 1; printf(«Enter n: «); scanf(«%d», printf(«Pervye %d chisel Fibonachi: «, n); for (i=1; i= f1) < printf(«%d «, f1); f1 = f0 + f1; >else < printf(«%d «, f0); f0 = f1 + f0; >> return 0; >
№19: Распечатать числа Фибоначчи (см. задачу 3.34), являющиеся простыми числами со значениями меньше n.
#include int main() < int n, i, f0 = 1, f1 = 1, k, k1; printf(«Enter n: «); scanf(«%d», while (f0 = f1) < k = f1; f1 = f0 + f1; >else < k = f0; f0 = f1 + f0; >for (i = 1; i return 0; >
Источник: xn--90aihhxfgb.xn--p1ai